Distributed Systems Distributed algorithms November 2005 Distributed systems

Distributed Systems: Distributed algorithms November 2005 Distributed systems: distributed algorithms 1

Overview of chapters • • Introduction Co-ordination models and languages General services Distributed algorithms – Ch 10 Time and global states, 11. 4 -11. 5 – Ch 11 Coordination and agreement, 12. 1 -12. 5 • Shared data • Building distributed services November 2005 Distributed systems: distributed algorithms 2

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 3

Logical clocks • Problem: ordering of events – requirement for many algorithms – physical clocks cannot be used • use causality: – within a single process: observation – between different processes: sending of a message happens before receiving the same message November 2005 Distributed systems: distributed algorithms 4

Logical clocks (cont. ) • Formalization: happens before relation x y • Rules: – if x happens before y in any process p then x y – for any message m: send (m) receive (m) – if x y and y z then x z • Implementation: logical clocks November 2005 Distributed systems: distributed algorithms 5

Logical clocks (cont. ) • Logical clock – counter appropriately incremented – one counter process • Physical clock – counts oscillations occurring in a crystal at a definitive frequency November 2005 Distributed systems: distributed algorithms 6

Logical clocks (cont. ) • Rules for incrementing local logical clock 1 for each event (including send) in process p: Cp : = Cp + 1 2 when a process sends a message m, it piggybacks on m the value of Cp 3 on receiving (m, t), a process q • computes Cq : = max (Cq, t) • applies rule 1: Cq : = Cq +1 Cq is logical time for event receive(m) November 2005 Distributed systems: distributed algorithms 7

Logical clocks (cont. ) • Logical timestamps: example 1 P 2 P 3 2 • a P 1 3 • c 0 • g 3 • • d 4 • e 1 5 • b November 2005 • f Distributed systems: distributed algorithms 8

Logical clocks (cont. ) • C(x) logical clock value for event x • Correct usage: if x y then C(x) < C(y) • Incorrect usage: if C(x) < C(y) then x y • Solution: Logical vector clocks November 2005 Distributed systems: distributed algorithms 9

Logical clocks (cont. ) • Vector clocks for N processes: – at process Pi: Vi[j] for j = 1, 2, …, N – Properties: if x y then V(x) < V(y) if V(x) < V(y) then x y November 2005 Distributed systems: distributed algorithms 10

Logical clocks (cont. ) • Rules for incrementing logical vector clock 1 for each event (including send) in process Pi: Vi[i] : = Vi[i] + 1 2 when a process Pi sends a message m, it piggybacks on m the value of Vi 3 on receiving (m, t), a process Pi • apply rule 1 • Vi[j] : = max(Vi[j] , t[j]) for j = 1, 2, …, N November 2005 Distributed systems: distributed algorithms 11

Logical clocks (cont. ) • Logical vector clocks : example November 2005 Distributed systems: distributed algorithms 12

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 13

Global states • Detect global properties November 2005 Distributed systems: distributed algorithms 14

Global states (cont. ) • Local states & events – Process Pi : e ik si k events state, before event k – History of Pi : hi = < ei 0, ei 1, ei 2, …> – Finite prefix of history of Pi : hik = < ei 0, ei 1, ei 2, …, eik > November 2005 Distributed systems: distributed algorithms 15

Global states (cont. ) • Global states & events – Global history H = h 1 h 2 h 3 … hn – Global state (when? ) S = ( s 1 p, s 2 q, …, snu) consistent? – Cut of the systems execution C = h 1 c 1 h 1 c 2 … h 1 cn November 2005 Distributed systems: distributed algorithms 16

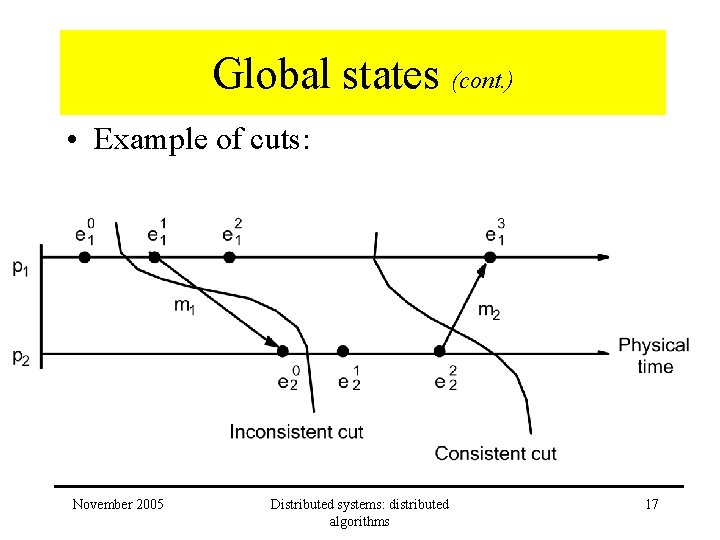
Global states (cont. ) • Example of cuts: November 2005 Distributed systems: distributed algorithms 17

Global states (cont. ) • Finite prefix of history of Pi : hik = < ei 0, ei 1, ei 2, …, eik > • Cut of the systems execution C = h 1 c 1 h 1 c 2 … h 1 cn • Consistent cut C e C, f e f C • Consistent global state corresponds to consistent cut November 2005 Distributed systems: distributed algorithms 18

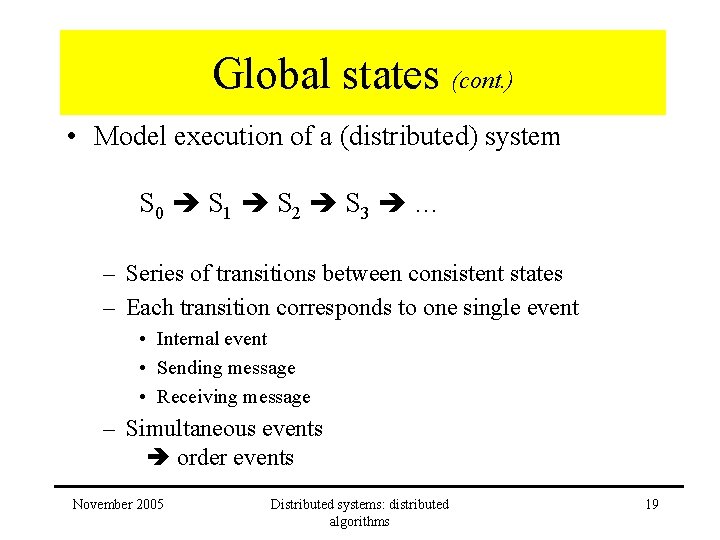
Global states (cont. ) • Model execution of a (distributed) system S 0 S 1 S 2 S 3 … – Series of transitions between consistent states – Each transition corresponds to one single event • Internal event • Sending message • Receiving message – Simultaneous events order events November 2005 Distributed systems: distributed algorithms 19

Global states (cont. ) • Definitions: – Run = ordering of all events (in a global history) consistent with each local history’s ordering – Linearization = consistent run + consistent with – S’ reachable from S linearization: … S … S’ … November 2005 Distributed systems: distributed algorithms 20

Global states (cont. ) • Kinds of global state predicates: – Stable = true in S S’, S … S’ = true in S’ – Safety = undesirable property S 0 = initial state of system S, S 0 … S = false in S – Liveness November 2005 = desirable property S 0 = initial state of system S, S 0 … S = true in S Distributed systems: distributed algorithms 21

Global states (cont. ) • Snapshot algorithm of Chandy & Lamport – Record consistent global state – Assumptions: • Neither channels nor processes fail • Channels are unidirectional and provide FIFOordered message delivery • Graph of channels and processes is strongly connected • Any process may initiate a global snapshot • Process may continue their execution during the snapshot November 2005 Distributed systems: distributed algorithms 22

Global states (cont. ) • Snapshot algorithm of Chandy & Lamport – Elements of algorithm • Players: processes Pi with – Incoming channels – Outgoing channels • Marker messages • 2 rules – Marker receiving rule – Marker sending rule – Start of algorithm • A process acts as it received a marker message November 2005 Distributed systems: distributed algorithms 23

Global states (cont. ) Marker receiving rule for process pi On pi’s receipt of a marker message over channel c: if (pi has not yet recorded its state) it records its process state now; records the state of c as the empty set; turns on recording of messages arriving over other incoming channels; else pi records the state of c as the set of messages it has received over c since it saved its state. end if Marker sending rule for process pi After pi has recorded its state, for each outgoing channel c: pi sends one marker message over c (before it sends any other message over c). November 2005 Distributed systems: distributed algorithms 24

Global states (cont. ) • Example: November 2005 Distributed systems: distributed algorithms 25

Global states (cont. ) 1. Global state S 0 2. Global state S 1 3. Global state S 2 4. Global state S 3 <$1000, 0> <$900, 5> C 1=<(five widgets)> p 1 p 1 c 2 (empty) c 1 (empty) c 2 (Order 10, $100), M c 1 (five widgets) c 2 (Order 10, $100) c 1 (empty) p 2 <$50, 2000> p 2 <$50, 1995> C 2 = <> (M = marker message) November 2005 Distributed systems: distributed algorithms 26

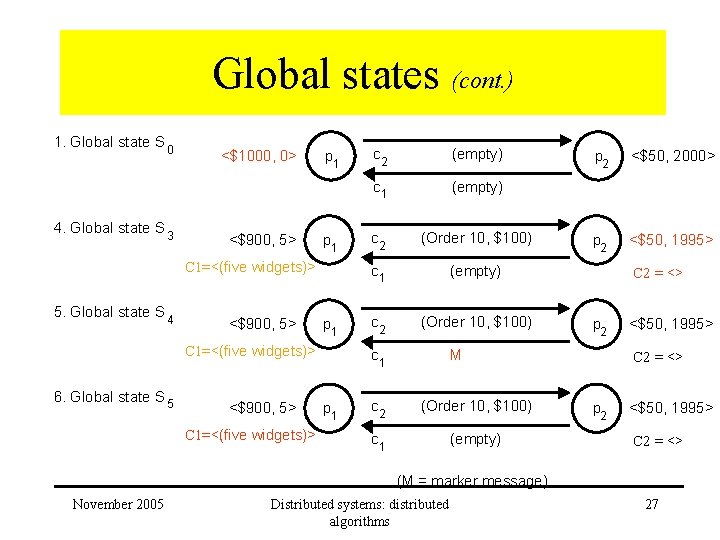
Global states (cont. ) 1. Global state S 0 4. Global state S 3 <$1000, 0> <$900, 5> p 1 C 1=<(five widgets)> 5. Global state S 4 <$900, 5> p 1 C 1=<(five widgets)> 6. Global state S 5 <$900, 5> C 1=<(five widgets)> c 2 (empty) c 1 (empty) c 2 (Order 10, $100) c 1 p 2 <$50, 2000> p 2 <$50, 1995> C 2 = <> p 2 M c 2 (Order 10, $100) c 1 (empty) <$50, 1995> C 2 = <> p 2 <$50, 1995> C 2 = <> (M = marker message) November 2005 Distributed systems: distributed algorithms 27

Global states (cont. ) • Observed state – Corresponds to consistent cut – Reachable! November 2005 Distributed systems: distributed algorithms 28

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 29

Failure detectors • Properties – Unreliable failure detector: answers with • Suspected • Unsuspected No “P is here” within T + E sec – Reliable failure detector: answers with • Failed • Unsuspected No “P is here” within T + A sec • Implementation – Every T sec: multicast by P of “P is here” – Maximum on message transmission time: • Asynchronous system: estimate E • Synchronous system: absolute bound A November 2005 Distributed systems: distributed algorithms 30

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 31

Mutual exclusion • Problem: how to give a single process temporarily a privilege? – Privilege = the right to access a (shared) resource – resource = file, device, window, … • Assumptions – clients execute the mutual exclusion algorithm – the resource itself might be managed by a server – Reliable communication November 2005 Distributed systems: distributed algorithms 32

Mutual exclusion (cont. ) • Basic requirements: – ME 1: at most one process might execute in the shared resource at any time (Safety) – ME 2: a process requesting access to the shared resource is eventually granted it (Liveness) – ME 3: Access to the shared resource should be granted in happened-before order (Ordering or fairness) November 2005 Distributed systems: distributed algorithms 33

Mutual exclusion (cont. ) • Solutions: – – central server algorithm distributed algorithm using logical clocks ring-based algorithm voting algorithm • Evaluation – Bandwidth (= #messages to enter and exit) – Client delay (incurred by a process at enter and exit) – Synchronization delay (delay between exit and enter) November 2005 Distributed systems: distributed algorithms 34

Mutual exclusion (cont. ) central server algorithm • Central server offering 2 operations: – enter() • if resource free then operation returns without delay else request is queued and return from operation is delayed – exit() • if request queue is empty then resource is marked free else return for a selected request is executed November 2005 Distributed systems: distributed algorithms 35

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: User Enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 36

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: User 3 Enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 37

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: User 3 P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 38

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: User 3 enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 39

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: 4 User 3 enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 40

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: 4 User 3 enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 41

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: 4, 2 User 3 enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 42

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: 4, 2 User 3 enter() exit() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 43

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: 4, 2 User enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 44

Mutual exclusion (cont. ) central server algorithm • Example: Server Queue: 2 User 4 enter() P 1 P 2 November 2005 P 3 Distributed systems: distributed algorithms P 4 45

Mutual exclusion (cont. ) central server algorithm • Evaluation: – ME 3 not satisfied! – Performance: • single server is performance bottleneck • Enter critical section: 2 messages • Synchronization: 2 messages between exit of one process and enter of next – Failure: • Central server is single point of failure • what if a client, holding the resource, fails? • Reliable communication required November 2005 Distributed systems: distributed algorithms 46

Mutual exclusion (cont. ) ring-based algorithm • All processes arranged in a – unidirectional – logical ring • token passed in ring • process with token has access to resource November 2005 Distributed systems: distributed algorithms 47

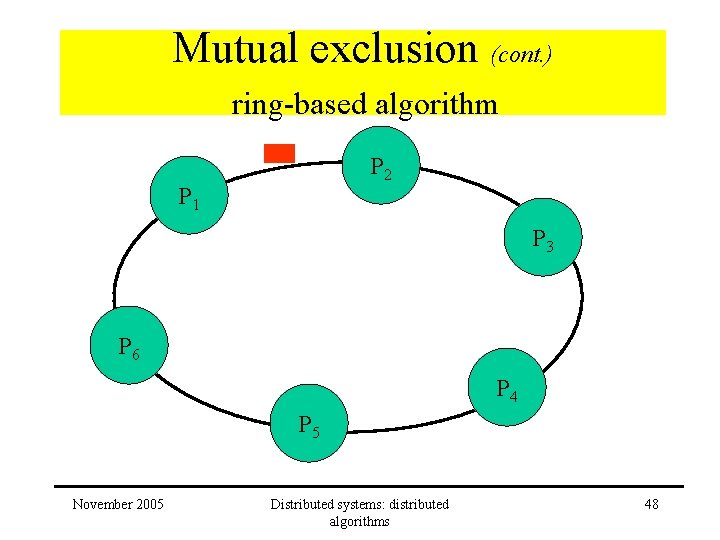
Mutual exclusion (cont. ) ring-based algorithm P 2 P 1 P 3 P 6 P 4 P 5 November 2005 Distributed systems: distributed algorithms 48

Mutual exclusion (cont. ) ring-based algorithm P 2 P 1 P 3 P 2 can use resource P 6 P 4 P 5 November 2005 Distributed systems: distributed algorithms 49

Mutual exclusion (cont. ) ring-based algorithm P 2 P 1 P 3 P 2 stopped using resource and forwarded token P 6 P 4 P 5 November 2005 Distributed systems: distributed algorithms 50

Mutual exclusion (cont. ) ring-based algorithm P 2 P 1 P 3 doesn’t need resource and forwards token P 6 P 4 P 5 November 2005 Distributed systems: distributed algorithms 51

Mutual exclusion (cont. ) ring-based algorithm P 2 P 1 P 3 P 6 P 4 P 5 November 2005 Distributed systems: distributed algorithms 52

Mutual exclusion (cont. ) ring-based algorithm • Evaluation: – ME 3 not satisfied – efficiency • high when high usage of resource • high overhead when very low usage – failure • Process failure: loss of ring! • Reliable communication required November 2005 Distributed systems: distributed algorithms 53

Mutual exclusion (cont. ) distributed algorithm using logical clocks • Distributed agreement algorithm – multicast requests to all participating processes – use resource when all other participants agree (= reply received) • Processes – keep logical clock; included in all request messages – behave as finite state machine: • released • wanted • held November 2005 Distributed systems: distributed algorithms 54

Mutual exclusion (cont. ) distributed algorithm using logical clocks • Ricart and Agrawala’s algorithm: process Pj – on initialization: • state : = released; – to obtain resource: • state : = wanted; • T = logical clock value for next event; • multicast request to other processes <T, Pj>; • wait for n-1 replies; • state : = held; November 2005 Distributed systems: distributed algorithms 55

Mutual exclusion (cont. ) distributed algorithm using logical clocks • Ricart and Agrawala’s algorithm: process Pj – on receipt of request <Ti, Pi> : • if (state = held) or (state = wanted and (T, Pj) < (Ti, Pi) ) then queue request from Pi else reply immediately to Pi – to release resource: • state : = released; • reply to any queued requests; November 2005 Distributed systems: distributed algorithms 56

Mutual exclusion (cont. ) distributed algorithm using logical clocks • Ricart and Agrawala’s algorithm: example – 3 processes – P 1 and P 2 will request it concurrently – P 3 not interested in using resource November 2005 Distributed systems: distributed algorithms 57

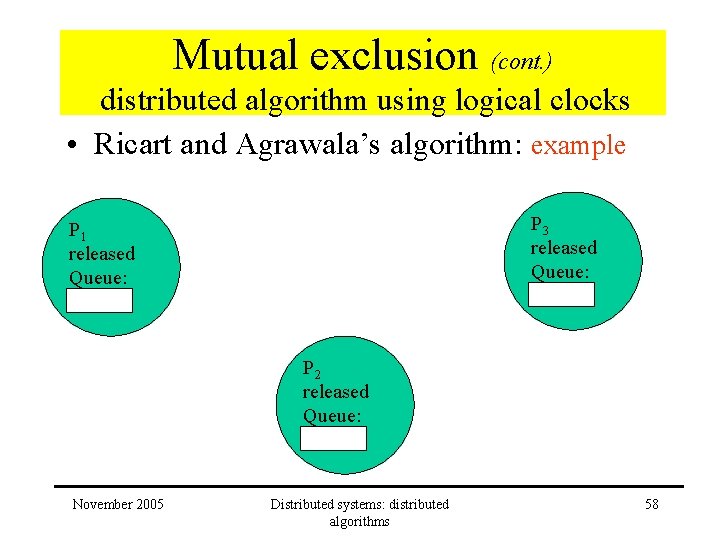
Mutual exclusion (cont. ) distributed algorithm using logical clocks • Ricart and Agrawala’s algorithm: example P 3 released Queue: P 1 released Queue: P 2 released Queue: November 2005 Distributed systems: distributed algorithms 58

Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 0 Queue: <41, P 1> November 2005 <41, P 1> P 3 released Queue: P 2 released Queue: Distributed systems: distributed algorithms 59

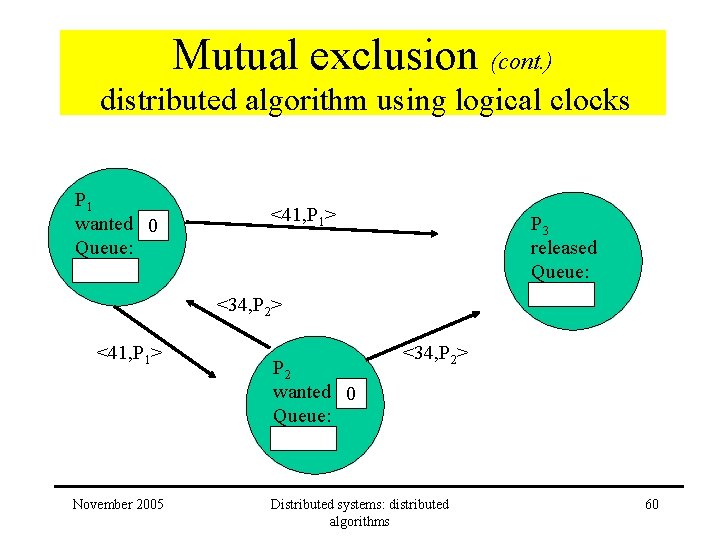
Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 0 Queue: <41, P 1> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 0 Queue: <34, P 2> Distributed systems: distributed algorithms 60

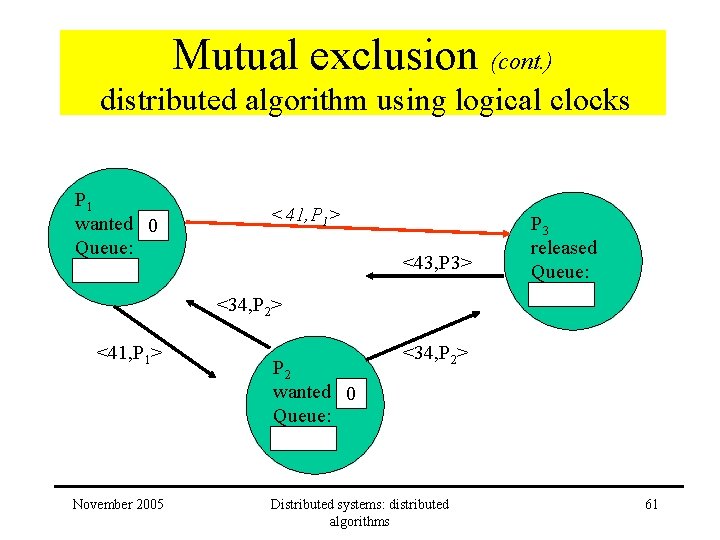
Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 0 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 0 Queue: <34, P 2> Distributed systems: distributed algorithms 61

Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 0 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 0 Queue: <34, P 2> Distributed systems: distributed algorithms <45, P 3> 62

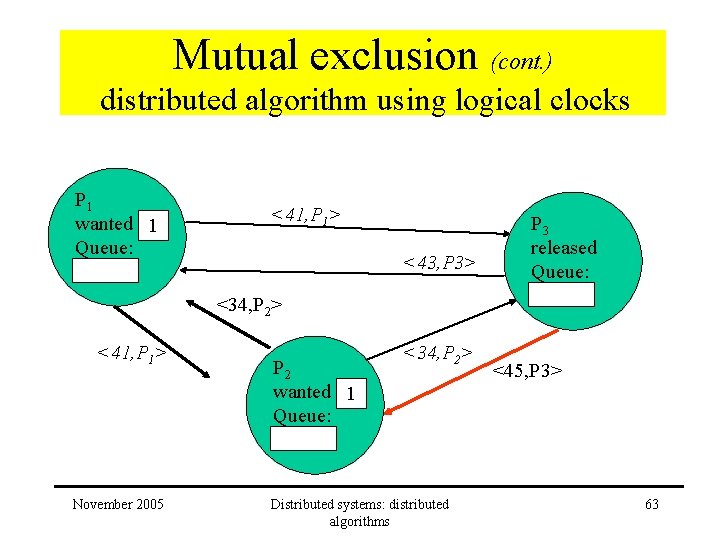
Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 1 Queue: <34, P 2> Distributed systems: distributed algorithms <45, P 3> 63

Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 1 Queue: P 1 <34, P 2> Distributed systems: distributed algorithms <45, P 3> 64

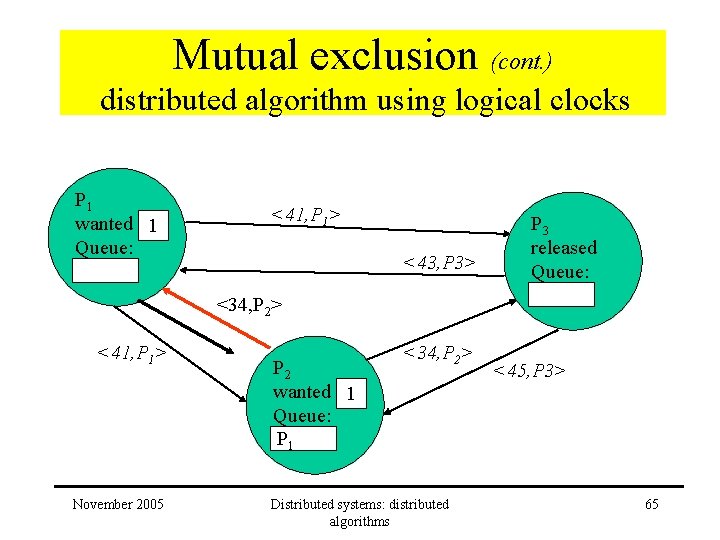
Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 1 Queue: P 1 <34, P 2> Distributed systems: distributed algorithms <45, P 3> 65

Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 wanted 1 Queue: P 1 <34, P 2> Distributed systems: distributed algorithms <45, P 3> 66

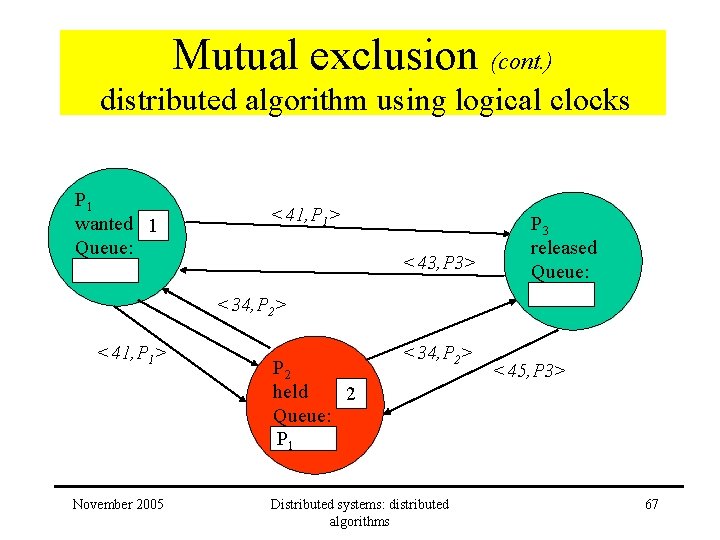
Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: <41, P 1> <43, P 3> P 3 released Queue: <34, P 2> <41, P 1> November 2005 P 2 held 2 Queue: P 1 <34, P 2> Distributed systems: distributed algorithms <45, P 3> 67

Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: P 3 released Queue: P 2 held 2 Queue: P 1 November 2005 Distributed systems: distributed algorithms 68

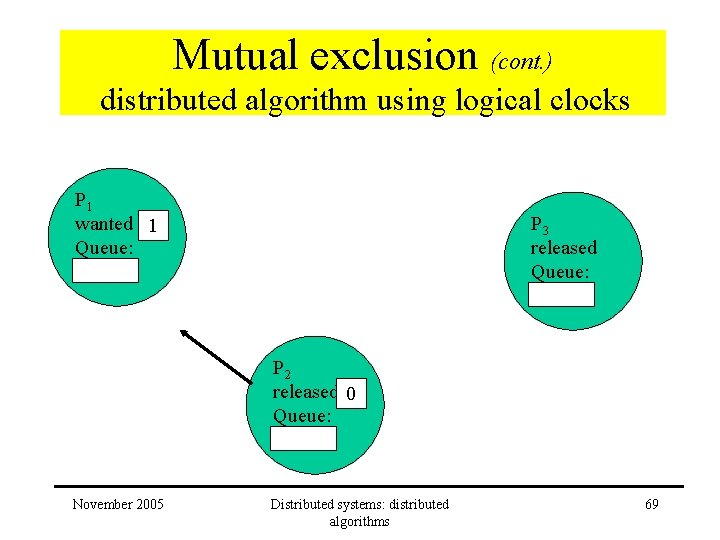
Mutual exclusion (cont. ) distributed algorithm using logical clocks P 1 wanted 1 Queue: P 3 released Queue: P 2 released 0 Queue: November 2005 Distributed systems: distributed algorithms 69

Mutual exclusion (cont. ) distributed algorithm using logical clocks • Evaluation – Performance: • expensive algorithm: 2 * ( n - 1 ) messages to get resource • Client delay: round trip • Synchronization delay: 1 message to pass section to another process • does not solve the performance bottleneck – Failure • each process must know all other processes • Reliable communication required November 2005 Distributed systems: distributed algorithms 70

Mutual exclusion (cont. ) voting algorithm • Approach of Maekawa: – Communication with subset of partners should suffice – Candidate collects sufficient votes • Voting set: Vi = voting set for pi – – i, j: Vi Vj | Vi | = K Pj contained in M voting sets Optimal solution • K ~ N • M=K November 2005 Distributed systems: distributed algorithms 71

Mutual exclusion (cont. ) voting algorithm On initialization Maekawa’s state : = RELEASED; voted : = FALSE; For pi to enter the critical section state : = WANTED; Multicast request to all processes in Vi – {pi}; Wait until (number of replies received = (K – 1)); state : = HELD; On receipt of a request from pi at pj (i ≠ j) if (state = HELD or voted = TRUE) then queue request from pi without replying; else send reply to pi; voted : = TRUE; end if November 2005 Distributed systems: distributed algorithms algorithm 72

Mutual exclusion (cont. ) voting algorithm Maekawa’s For pi to exit the critical section state : = RELEASED; Multicast release to all processes in Vi – {pi}; algorithm (cont. ) On receipt of a release from pi at pj (i ≠ j) if (queue of requests is non-empty) then remove head of queue – from pk, say; send reply to pk; voted : = TRUE; else voted : = FALSE; end if November 2005 Distributed systems: distributed algorithms 73

Mutual exclusion (cont. ) voting algorithm • Evaluation – Properties • ME 1: OK • ME 2: NOK, deadlock possible solution: process requests in order • ME 3: Ok – Performance • Bandwidth: on enter 2 N messages + on exit N messages • Client delay: round trip • Synchronization delay: round trip – Failure: • Crash of process on another voting set can be tolerated • Reliable communication required November 2005 Distributed systems: distributed algorithms 74

Mutual exclusion (cont. ) • Discussion – algorithms are expensive and not practical – algorithms are extremely complex in the presence of failures – better solution in most cases: • let the server, managing the resource, perform concurrency control • gives more transparency for the clients November 2005 Distributed systems: distributed algorithms 75

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 76

Elections • Problem statement: – select a process from a group of processes – several processes may start election concurrently • Main requirement: – unique choice – Select process with highest id • Process id • <1/load, process id> November 2005 Distributed systems: distributed algorithms 77

Elections (cont. ) • Basic requirements: – E 1: – E 2: participant pi set electedi = or electedi = P; P process with highest id (Safety) all processes pi participate and set electedi or crash (Liveness) not yet defined November 2005 Distributed systems: distributed algorithms 78

Elections (cont. ) • Solutions: – Bully election algorithm – Ring based election algorithm • Evaluation – Bandwidth ( ~ total number of messages) – Turnaround time (the number of serialized message transmission times between initiation and termination of a single run) November 2005 Distributed systems: distributed algorithms 79

Elections (cont. ) Bully election • Assumptions: – each process has identifier – processes can fail during an election – communication is reliable • Goal: – surviving member with the largest identifier is elected as coordinator November 2005 Distributed systems: distributed algorithms 80

Elections (cont. ) Bully election • Roles for processes: – coordinator • elected process • has highest identifier, at the time of election – initiator • process starting the election for some reason November 2005 Distributed systems: distributed algorithms 81

Elections (cont. ) Bully election • Three types of messages: – election message • sent by an initiator of the election to all other processes with a higher identifier – answer message • a reply message sent by the receiver of an election message – coordinator message • sent by the process becoming the coordinator to all other processes with lower identifiers November 2005 Distributed systems: distributed algorithms 82

Elections (cont. ) Bully election • Algorithm: – send election message: • process doing it is called initiator • any process may do it at any time • when a failed process is restarted, it starts an election, even though the current coordinator is functioning (bully) – a process receiving an election message • replies with an answer message • will start an election itself (why? ) November 2005 Distributed systems: distributed algorithms 83

Elections (cont. ) Bully election • Algorithm: – actions of an initiator • when not receiving an answer message within a certain time (2 Ttrans +Tprocess) becomes coordinator • when having received an answer message ( a process with a higher identifier is active) and not receiving a coordinator message (after x time units) will restart elections November 2005 Distributed systems: distributed algorithms 84

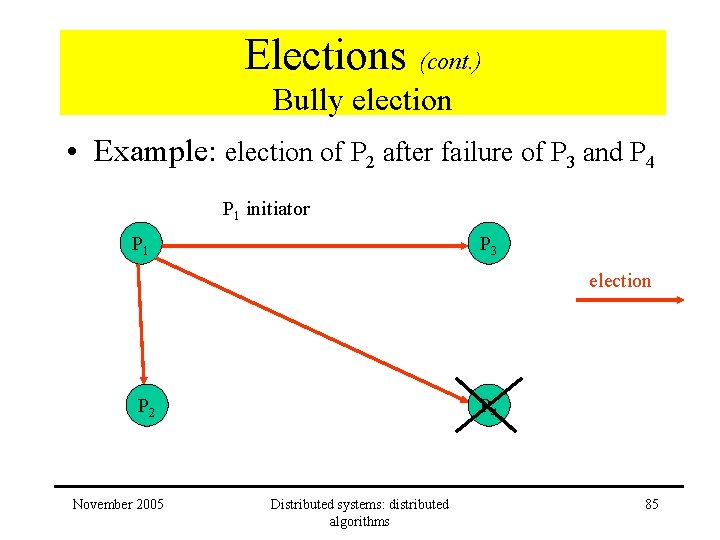
Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 P 1 initiator P 1 P 3 election P 2 November 2005 P 4 Distributed systems: distributed algorithms 85

Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 P 2 and P 3 reply and start election P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 86

Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 Election messages of P 2 arrive P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 87

Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 P 3 replies P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 88

Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 P 3 fails P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 89

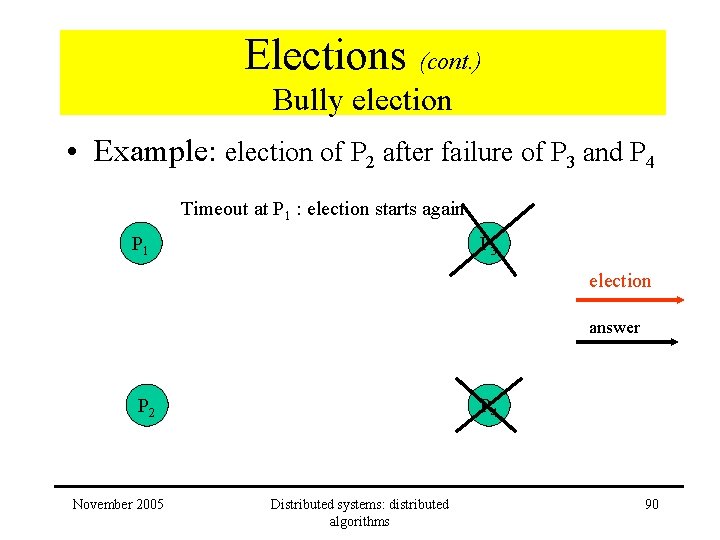
Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 Timeout at P 1 : election starts again P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 90

Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 Timeout at P 1 : election starts again P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 91

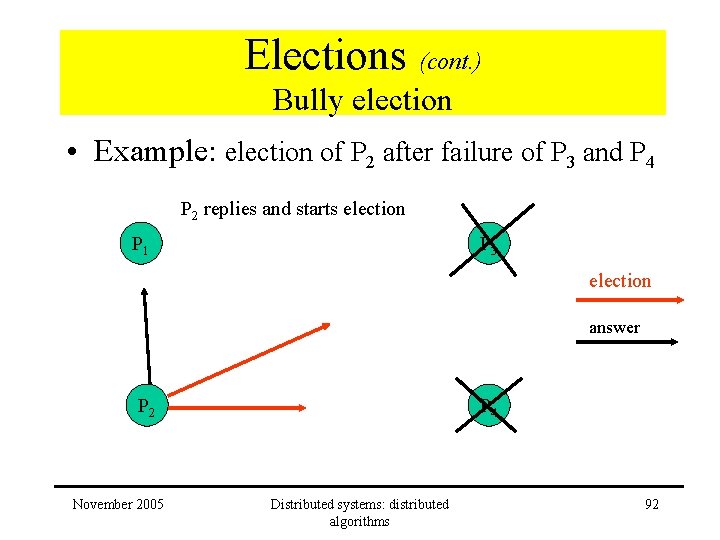
Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 P 2 replies and starts election P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 92

Elections (cont. ) Bully election • Example: election of P 2 after failure of P 3 and P 4 P 2 receives no replies coordinator P 1 P 3 election answer P 2 November 2005 P 4 Distributed systems: distributed algorithms 93

Elections (cont. ) Bully election • Evaluation – Correctness: E 1 & E 2 ok, if • Reliable communication • No process replaces crashed process – Correctness: no guarantee for E 1, if • Crashed process is replaced by process with same id • Assumed timeout values are inaccurate (= unreliable failure detector) – Performance • Worst case: O(n 2) • Optimal: bandwidth: n-2 messages turnaround: 1 message November 2005 Distributed systems: distributed algorithms 94

Elections (cont. ) Ring based election • Assumptions: – processes arranged in a logical ring – each process has an identifier: i for Pi – processes remain functional and reachable during the algorithm November 2005 Distributed systems: distributed algorithms 95

Elections (cont. ) Ring based election • Messages: – forwarded over logical ring – 2 types: • election: • elected: used during election contains identifier used to announce new coordinator • Process States: – participant – non-participant November 2005 Distributed systems: distributed algorithms 96

Elections (cont. ) Ring based election • Algorithm – process initiating an election • becomes participant • sends election message to its neighbour November 2005 Distributed systems: distributed algorithms 97

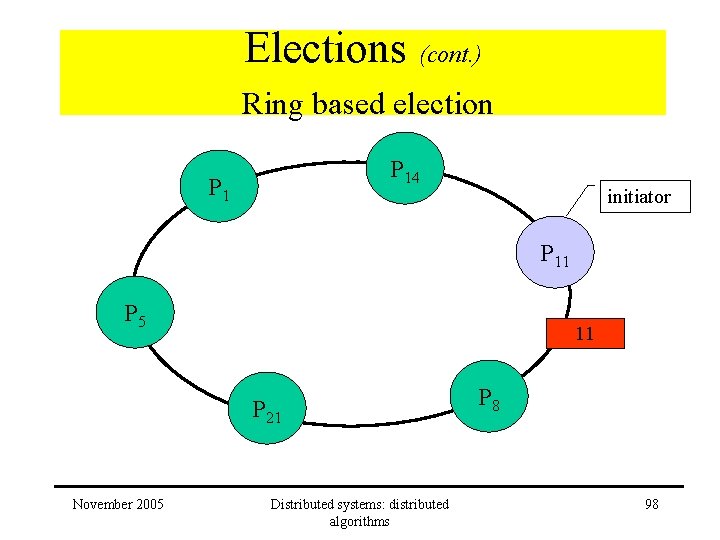
Elections (cont. ) Ring based election P 14 P 1 initiator P 11 P 5 11 P 21 November 2005 Distributed systems: distributed algorithms P 8 98

Elections (cont. ) Ring based election • Algorithm – upon receiving an election message, a process compares identifiers: • Received: identifier in message • own: identifier of process – 3 cases: • Received > own • Received < own • Received = own November 2005 Distributed systems: distributed algorithms 99

Elections (cont. ) Ring based election • Algorithm – receive election message • Received > own – message forwarded – process becomes participant November 2005 Distributed systems: distributed algorithms 100

Elections (cont. ) Ring based election P 14 P 1 initiator P 11 P 5 11 P 21 November 2005 Distributed systems: distributed algorithms P 8 101

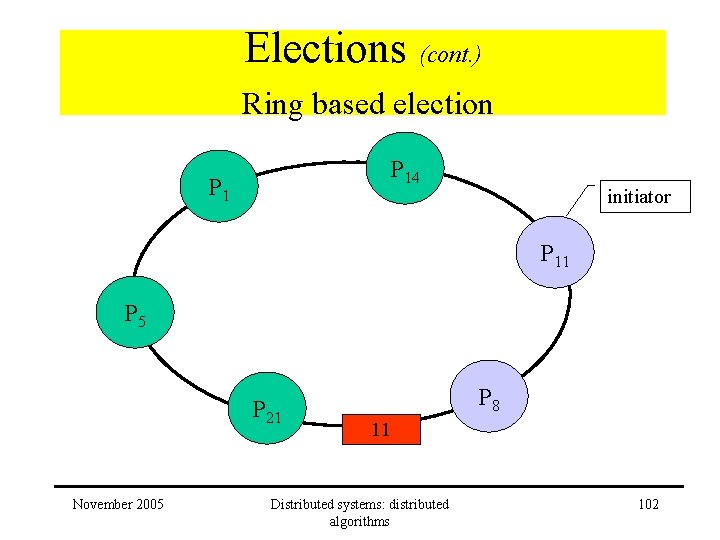
Elections (cont. ) Ring based election P 14 P 1 initiator P 11 P 5 P 21 November 2005 P 8 11 Distributed systems: distributed algorithms 102

Elections (cont. ) Ring based election • Algorithm – receive election message • Received > own – message forwarded – process becomes participant • Received < own and process is non-participant – substitutes own identifier in message – message forwarded – process becomes participant November 2005 Distributed systems: distributed algorithms 103

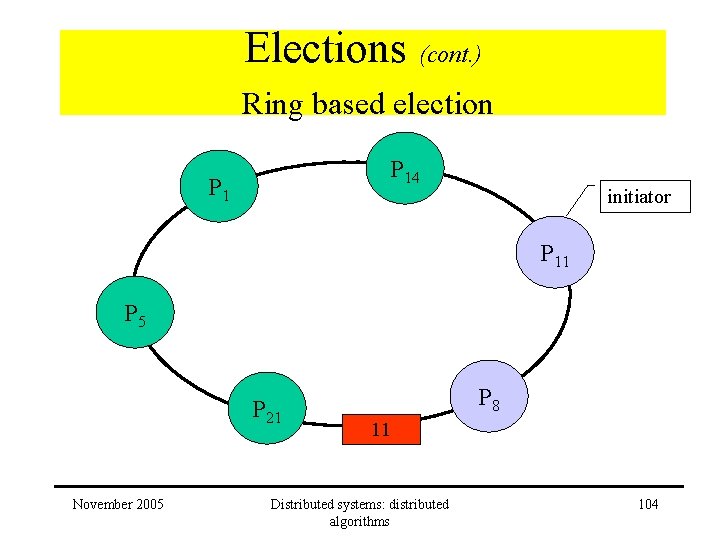
Elections (cont. ) Ring based election P 14 P 1 initiator P 11 P 5 P 21 November 2005 P 8 11 Distributed systems: distributed algorithms 104

Elections (cont. ) Ring based election P 14 P 1 initiator P 11 P 5 21 P 21 November 2005 Distributed systems: distributed algorithms P 8 105

Elections (cont. ) Ring based election P 14 P 1 initiator 21 P 11 P 5 P 21 November 2005 Distributed systems: distributed algorithms P 8 106

Elections (cont. ) Ring based election P 14 P 1 initiator P 11 P 5 P 21 November 2005 P 8 21 Distributed systems: distributed algorithms 107

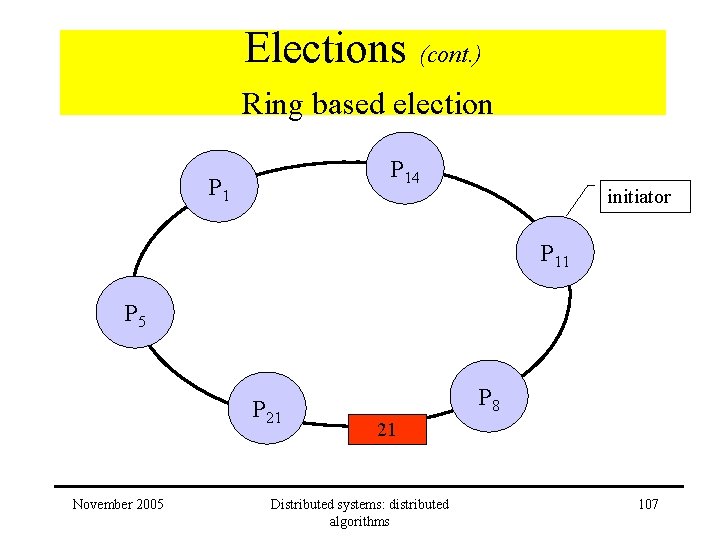
Elections (cont. ) Ring based election • Algorithm: – receive election message • Received > own –. . . • Received < own and process is non-participant –. . . • Received = own – – November 2005 identifier must be greatest process becomes coordinator new state: non-participant sends elected message to neighbour Distributed systems: distributed algorithms 108

Elections (cont. ) Ring based election P 14 P 11 P 5 coordinator 21 November 2005 P 21 Distributed systems: distributed algorithms P 8 109

Elections (cont. ) Ring based election • Algorithm receive election message • Received > own – message forwarded – process becomes participant • Received < own and process is non-participant – substitutes own identifier in message – message forwarded – process becomes participant • Received = own – identifier must be greatest – process becomes coordinator – new state: non-participant – sends elected message to neighbour November 2005 Distributed systems: distributed algorithms 110

Elections (cont. ) Ring based election • Algorithm – receive elected message • participant: – new state: non-participant – forwards message • coordinator: – election process completed November 2005 Distributed systems: distributed algorithms 111

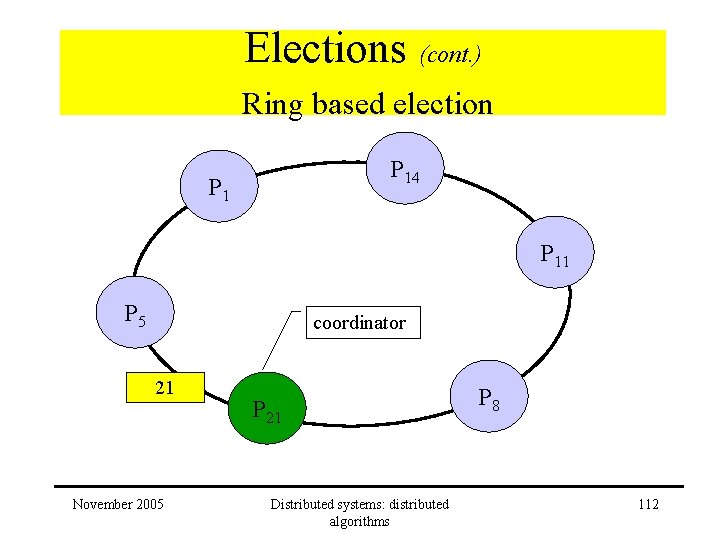
Elections (cont. ) Ring based election P 14 P 11 P 5 coordinator 21 November 2005 P 21 Distributed systems: distributed algorithms P 8 112

Elections (cont. ) Ring based election P 14 P 1 21 P 11 P 5 coordinator P 21 November 2005 Distributed systems: distributed algorithms P 8 113

Elections (cont. ) Ring based election 21 P 14 P 11 P 5 coordinator P 21 November 2005 Distributed systems: distributed algorithms P 8 114

Elections (cont. ) Ring based election P 14 P 1 21 P 11 P 5 coordinator P 21 November 2005 Distributed systems: distributed algorithms P 8 115

Elections (cont. ) Ring based election P 14 P 11 P 5 coordinator P 21 November 2005 Distributed systems: distributed algorithms 21 P 8 116

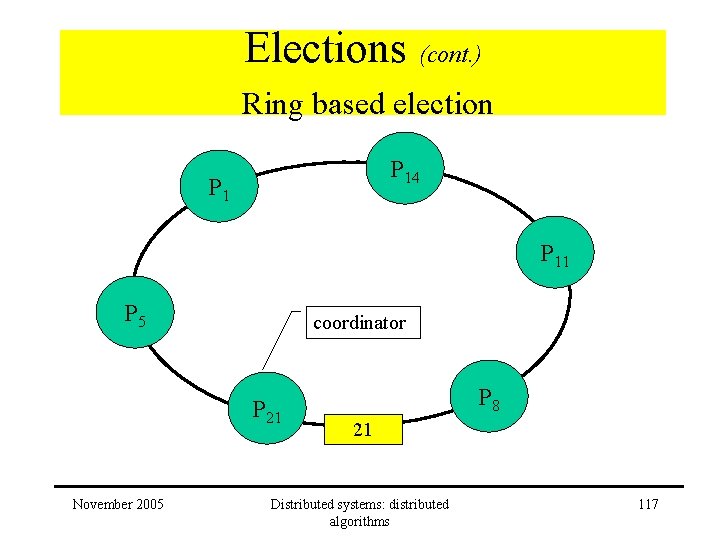
Elections (cont. ) Ring based election P 14 P 11 P 5 coordinator P 21 November 2005 P 8 21 Distributed systems: distributed algorithms 117

Elections (cont. ) Ring based election P 14 P 11 P 5 coordinator P 21 November 2005 Distributed systems: distributed algorithms P 8 118

Elections (cont. ) Ring based election • Evaluation – Why is condition Received < own and process is non-participant necessary? (see next slide for full algorithm) – Number of messages: • worst case: 3 * n - 1 • best case: 2 * n – concurrent elections: messages are extinguished • as soon as possible • before winning result is announced November 2005 Distributed systems: distributed algorithms 119

Elections (cont. ) Ring based election • Algorithm receive election message • Received > own – message forwarded – process becomes participant • Received < own and process is non-participant – substitutes own identifier in message – message forwarded – process becomes participant • Received = own – identifier must be greatest – process becomes coordinator – new state: non-participant – sends elected message to neighbour November 2005 Distributed systems: distributed algorithms 120

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 121

Multicast communication • Essential property: – 1 multicast operation <> multiple sends Higher efficiency Stronger delivery guarantees • Operations: g = group, m = message – X-multicast(g, m) – X-deliver(m) • <> receive(m) – X additional property Basic, Reliable, Fif. O, …. November 2005 Distributed systems: distributed algorithms 122

Multicast communication(cont. ) IP multicast • Datagram operations – with multicast IP address • Failure model cfr UDP – Omission failures – No ordering or reliability guarantees November 2005 Distributed systems: distributed algorithms 123

Multicast communication(cont. ) Basic multicast • = IP multicast + delivery guarantee if multicasting process does not crash • Straightforward algorithm: (with reliable send) To B-multicast(g, m): p g: send(p, m) On receive(m) at p: B-deliver(m) • Ex. practical algorithm using IP-multicast November 2005 Distributed systems: distributed algorithms 124

Multicast communication(cont. ) Reliable multicast • Properties: – Integrity (safety) • A correct process delivers a message at most once – Validity (liveness) • Correct process p multicasts m p delivers m – Agreement (liveness) • correct process p delivering m all correct processes will deliver m – Uniform agreement (liveness) • process p (correct or failing) delivering m all correct processes will deliver m November 2005 Distributed systems: distributed algorithms 125

Multicast communication(cont. ) • Reliable multicast 2 algorithms: 1. Using B-multicast 2. Using IP-multicast + piggy backed acks November 2005 Distributed systems: distributed algorithms 126

Multicast communication(cont. ) Reliable multicast Algorithm 1 with B-multicast November 2005 Distributed systems: distributed algorithms 127

Multicast communication(cont. ) Reliable multicast Algorithm 1 with B-multicast • • Correct? – Integrity – Validity – Agreement Efficient? – NO: each message transmitted g times November 2005 Distributed systems: distributed algorithms 128

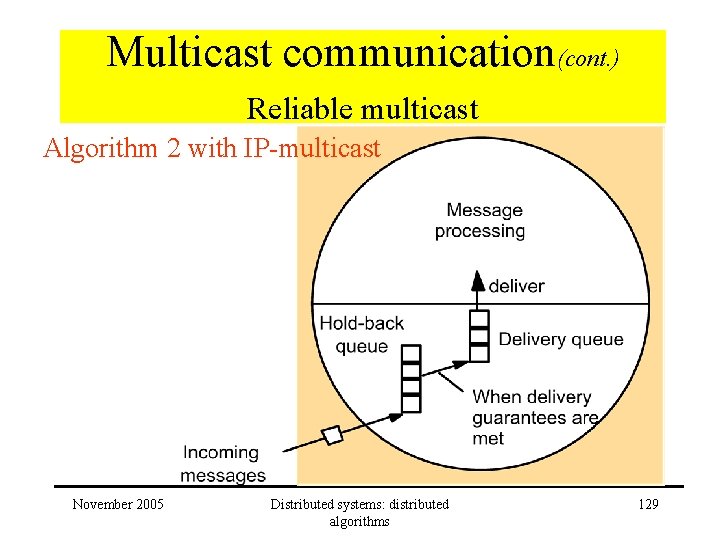
Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast November 2005 Distributed systems: distributed algorithms 129

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast Data structures at process p: Sgp : sequence number Rgq : sequence number of the latest message it has delivered from q On initialization: Sg p = 0 For process p to R-multicast message m to group g IP-multicast (g, <m, Sgp , <q, Rgq > >) Sgp ++ On IP-deliver (<m, S, <q, R>>) at q from p November 2005 Distributed systems: distributed algorithms 130

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast On IP-deliver (<m, S, <q, R>>) at q from p if S = Rgp + 1 then R-deliver (m) Rgp ++ check hold-back queue else if S > Rgp + 1 then store m in hold-back queue request missing messages endif if R > Rg then request missing messages November 2005 endif Distributed systems: distributed algorithms 131

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast • Correct? – Integrity: seq numbers + checksums – Validity: if missing messages are detected – Agreement: if copy of message remains available November 2005 Distributed systems: distributed algorithms 132

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • • 3 processes in group: P, Q, R State of process: – S: Next_sequence_number – Rq: Already_delivered from Q – Stored messages • Presentation: November 2005 P: 2 Q: 3 R: 5 <> Distributed systems: distributed algorithms 133

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • Initial state: P: 0 Q: -1 <> R: -1 Q: 0 P: -1 R: -1 <> November 2005 R: 0 P: -1 Q: -1 <> Distributed systems: distributed algorithms 134

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • First multicast by P: P: 1 Q: -1 R: -1 < mp 0 > Q: 0 P: -1 R: -1 <> November 2005 P: mp 0, 0, <Q: -1, R: -1> R: 0 P: -1 Q: -1 <> Distributed systems: distributed algorithms 135

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • Arrival multicast by P at Q: P: 1 Q: -1 R: -1 < mp 0 > R: 0 P: -1 Q: -1 <> Q: 0 P: 0 R: -1 < mp 0 > November 2005 P: mp 0, 0, <Q: -1, R: -1> Distributed systems: distributed algorithms 136

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • New state: P: 1 Q: -1 R: -1 < mp 0 > R: 0 P: -1 Q: -1 <> Q: 0 P: 0 R: -1 < mp 0 > November 2005 Distributed systems: distributed algorithms 137

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • Multicast by Q: mq 0, 0, <P: 0, R: -1> P: 1 Q: -1 R: -1 < mp 0 > Q: 1 P: 0 R: -1 < mp 0 , mq 0 > November 2005 R: 0 P: -1 Q: -1 <> Distributed systems: distributed algorithms 138

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • Arrival of multicast by Q: mq 0, 0, <P: 0, R: -1> P: 1 Q: 0 R: -1 < mp 0 , mq 0 > Q: 1 P: 0 R: -1 < mp 0 , , mq 0 > November 2005 R: 0 P: -1 Q: 0 < mq 0 > Distributed systems: distributed algorithms 139

Multicast communication(cont. ) Reliable multicast Algorithm 2 with IP-multicast: example • When to delete stored messages? P: 1 Q: 0 R: -1 < mp 0 , mq 0 > Q: 1 P: 0 R: -1 < mp 0 , , mq 0 > November 2005 R: 0 P: -1 Q: 0 < mq 0 > Distributed systems: distributed algorithms 140

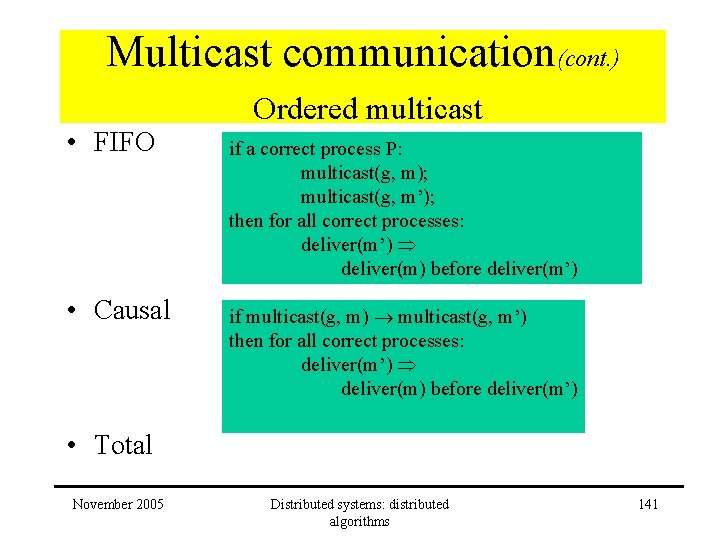
Multicast communication(cont. ) Ordered multicast • FIFO • Causal if a correct process P: multicast(g, m); multicast(g, m’); then for all correct processes: deliver(m’) deliver(m) before deliver(m’) if multicast(g, m) multicast(g, m’) then for all correct processes: deliver(m’) deliver(m) before deliver(m’) • Total November 2005 Distributed systems: distributed algorithms 141

Multicast communication(cont. ) Ordered multicast • Total if p: deliver(m) deliver( m’) then for all correct processes: deliver(m’) deliver(m) before deliver(m’) • FIFO-Total = FIFO + Total • Causal-Total = Causal + Total • Atomic = reliable + Total November 2005 Distributed systems: distributed algorithms 142

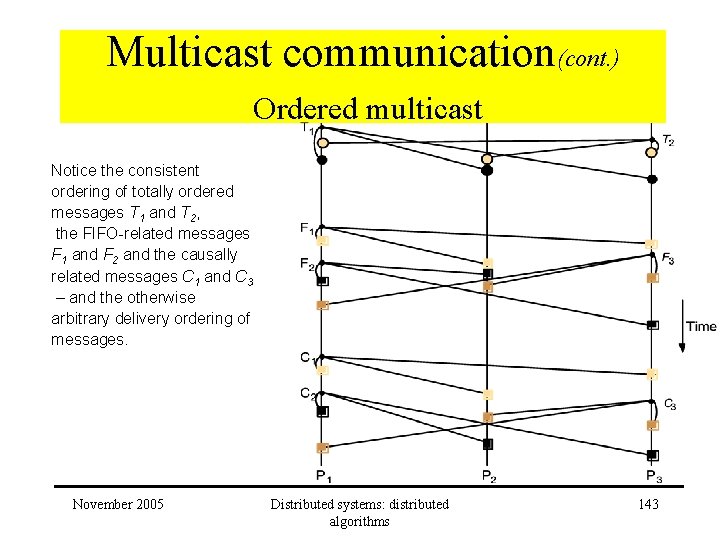
Multicast communication(cont. ) Ordered multicast Notice the consistent ordering of totally ordered messages T 1 and T 2, the FIFO-related messages F 1 and F 2 and the causally related messages C 1 and C 3 – and the otherwise arbitrary delivery ordering of messages. November 2005 Distributed systems: distributed algorithms 143

Multicast communication(cont. ) • FIFO multicast Alg. 1: R-multicast using IP-multicast – Correct? • • Sender assigns Sgp • Receivers deliver in this order Alg. 2 on top of any B-multicast November 2005 Distributed systems: distributed algorithms 144

Multicast communication(cont. ) FIFO multicast Algorithm 2 on top of any B-multicast Data structures at process p: Sgp : sequence number Rgq : sequence number of the latest message it has delivered from q On initialization: Sgp = 0; Rgq = -1 For process p to FO-multicast message m to group g B-multicast ( g, <m, Sgp >) Sgp ++ On B-deliver (<m, S >) at q from p November 2005 Distributed systems: distributed algorithms 145

Multicast communication(cont. ) FIFO multicast Algorithm 2 on top of any B-multicast On B-deliver (<m, S >) at q from p if S = Rgp + 1 then FO-deliver (m) Rgp ++ check hold-back queue else if S > Rgp + 1 then store m in hold-back queue endif November 2005 Distributed systems: distributed algorithms 146

Multicast communication(cont. ) TOTAL multicast • Basic approach: – – Sender: assign totally ordered identifiers iso process ids Receiver: deliver as for FIFO ordering • Alg. 1: use a (single) sequencer process • Alg. 2: participants collectively agree on the assignment of sequence numbers November 2005 Distributed systems: distributed algorithms 147

Multicast communication(cont. ) TOTAL multicast: sequencer process November 2005 Distributed systems: distributed algorithms 148

Multicast communication(cont. ) TOTAL multicast: sequencer process • Correct? • Problems? – A single sequencer process • bottleneck • single point of failure November 2005 Distributed systems: distributed algorithms 149

Multicast communication(cont. ) TOTAL multicast: ISIS algorithm • Approach: – Sender: • B-multicasts message – Receivers: • Propose sequence numbers to sender – Sender: • uses returned sequence numbers to generate agreed sequence number November 2005 Distributed systems: distributed algorithms 150

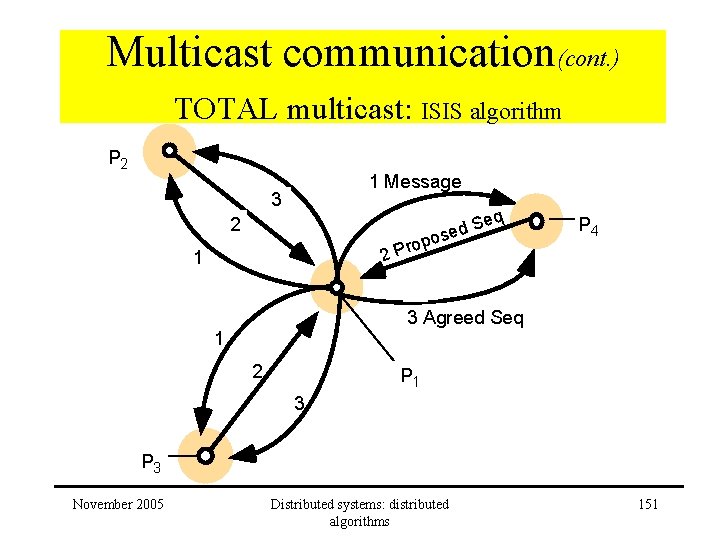
Multicast communication(cont. ) TOTAL multicast: ISIS algorithm P 2 1 Message 3 eq S d se o p o r 22 P 4 2 P 1 3 Agreed Seq 1 2 P 1 3 P 3 November 2005 Distributed systems: distributed algorithms 151

Multicast communication(cont. ) TOTAL multicast: ISIS algorithm Data structures at process p: Agp : largest agreed sequence number Pgp : largest proposed sequence number by P On initialization: Pg p = 0 For process p to TO-multicast message m to group g B-multicast ( g, <m, i >) /i = unique id for m On B-deliver (<m, i> ) at q from p Pgq = max (Agq, Pgq) + 1 send (p, < i, Pgq >) store <m, i, Pgq > in hold-back queue November 2005 Distributed systems: distributed algorithms 152

Multicast communication(cont. ) TOTAL multicast: ISIS algorithm On receive( i, P) at p from q wait for all replies; a is the largest reply B-multicast(g, < “order”, i, a >) On B-deliver (<“order”, i, a > ) at q from p Agq = max (Agq, a) attach a to message i in hold-back queue reorder messages in hold-back queue (increasing sequence numbers) while message m in front of hold-back queue has been assigned an agreed sequence number do remove m from hold-back queue TO-deliver (m) November 2005 Distributed systems: distributed algorithms 153

Multicast communication(cont. ) • • • TOTAL multicast: ISIS algorithm Correct? – Processes will agree on sequence number for a message – Sequence numbers are monotonically increasing – No process can prematurely deliver a message Performance – 3 serial messages! Total ordering – <> FIFO – <> causal November 2005 Distributed systems: distributed algorithms 154

Multicast communication(cont. ) • Causal multicast Limitations: – Causal order only by multicast operations – Non-overlapping, closed groups • Approach: – Use vector timestamps – Timestamp = count number of multicast messages November 2005 Distributed systems: distributed algorithms 155

Multicast communication(cont. ) Causal multicast: vector timestamps Meaning? November 2005 Distributed systems: distributed algorithms 156

Multicast communication(cont. ) Causal multicast: vector timestamps • Correct? – Message timestamp m m’ – Given V V’ multicast(g, m) multicast(g, m’) proof V < V’ November 2005 Distributed systems: distributed algorithms 157

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 158

Consensus & related problems • System model – N processes pi – Communication is reliable – Processes mail fail • Crash • Byzantine – No message signing • Message signing limits the harm a faulty process can do • Problems – Consensus – Byzantine generals – Interactive consistency November 2005 Distributed systems: distributed algorithms 159

Consensus • Problem statement – pi: undecided state & pi proposes vi – Message exchanges – Finally: each process pi sets decision variable di, enters decided state and may not change di • Requirements: – Termination: eventually each correct process pi sets di – Agreement: pi and pj correct & in decided state di = dj – Integrity: correct processes all propose same value d any process in decided state has chosen d November 2005 Distributed systems: distributed algorithms 160

Consensus • Simple algorithm (no process failures) – Collect processes in group g – For each process pi: • R-multicast(g, vi) • Collect N values • d = majority (v 1, v 2, . . . , v. N) • Problems with failures: – Crash: detected? not in asynchronous systems – Byzantine? Faulty process can send around different values November 2005 Distributed systems: distributed algorithms 161

Byzantine generals • Problem statement – Informal: • • agree to attack or to retreat commander issues the order lieutenants are to decide to attack or retreat all can be ‘treacherous’ – Formal • One process proposes value • Others are to agree • Requirements: – Termination: each process eventually decides – Agreement: all correct processes select the same value – Integrity: commander correct other correct processes select value of commander November 2005 Distributed systems: distributed algorithms 162

Interactive consistency • Problem statement – Correct processes agree upon a vector of values (one value for each process) • Requirements: – Termination: each process eventually decides – Agreement: all correct processes select the same value – Integrity: November 2005 if pi correct then all correct processes decide on vi as the i-the component of their vector Distributed systems: distributed algorithms 163

Related problems & solutions • Basic solutions: – Consensus: • Ci(v 1, v 2, . . . , v. N) = decision value of pi – Byzantine generals • j is commander, proposing v • BGi (j, v) = decision value of pi – Interactive consensus • ICi(v 1, v 2, . . . , v. N)[j] = jth value in the decision vector of pi with v 1, v 2, . . . , v. N values proposed by processes November 2005 Distributed systems: distributed algorithms 164

Related problems & solutions • Derived solutions: – IC from BG: • Run BG N times once with each process as commander • ICi(v 1, v 2, . . . , v. N)[j] = BG(j, vj) – C from IC: • Run IC and produce vector of values • Derive single value with appropriate function – BG from C: November 2005 Distributed systems: distributed algorithms 165

Related problems & solutions • Derived solutions: – IC from BG: – C from IC: – BG from C: • Commander pj sends value v to itself & other processes • Each process runs C with the values v 1, v 2, . . . v. N they received • BGi(j, v) = Ci(v 1, v 2, . . . v. N) November 2005 Distributed systems: distributed algorithms 166

Consensus in a synchronous system • Assumptions – Use B-multicast – f of N processes may fail • Approach – Proceed in f + 1 rounds – In each round correct processes B-multicast values • Variables – Valuesir = set of proposed values known to process pi at the beginning of round r November 2005 Distributed systems: distributed algorithms 167

Consensus in a synchronous system November 2005 Distributed systems: distributed algorithms 168

Consensus in a synchronous system • Termination? – Synchronous system • Correct? – Each process arrives at the same set of values at the end of the final round – Proof? • Assume sets are different. . . • Pi has value v & Pj doesn’t have value v • Pk : managed to send v to Pi and not to Pj • Agreement & Integrity? – Processes apply the same function November 2005 Distributed systems: distributed algorithms 169

Byzantine generals in a synchronous system • Assumptions – Arbitrary failures – f of N processes may be faulty – Channels are reliable: no message injections – Unsigned messages November 2005 Distributed systems: distributed algorithms 170

Byzantine generals in a synchronous system • Impossibility with 3 processes p 1 (Commander) 1: v 1: w 2: 1: v p 2 1: x 2: 1: w p 3 p 2 3: 1: u p 3 3: 1: x Faulty processes are shown shaded • Impossibility with N <= 3 f processes November 2005 Distributed systems: distributed algorithms 171

Byzantine generals in a synchronous system • Solution with one faulty process – N = 4, f = 1 – 2 rounds of messages: • Commander sends its value to each of the lieutenants • Each of the lieutenants sends the value it received to its peers – Lieutenant receives • Value of commander • N-2 values of peers Use majority function November 2005 Distributed systems: distributed algorithms 172

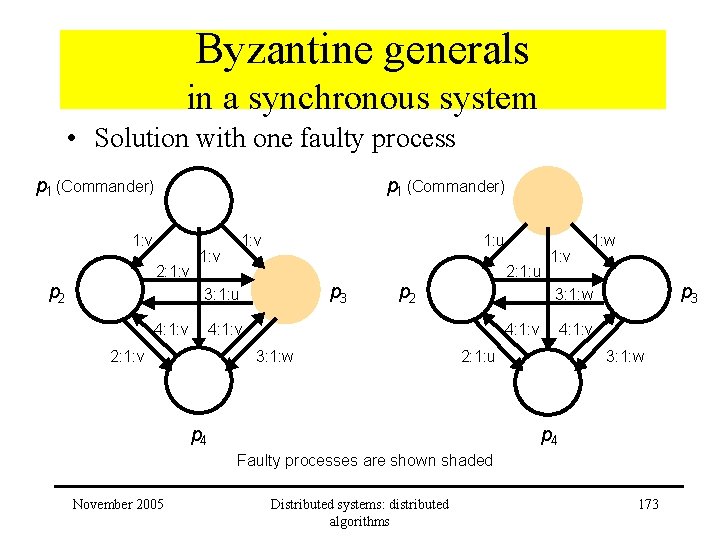
Byzantine generals in a synchronous system • Solution with one faulty process p 1 (Commander) 1: v 2: 1: v p 2 1: v 1: u p 3 3: 1: u 4: 1: v 2: 1: u p 2 4: 1: v 3: 1: w p 3 3: 1: w 4: 1: v 2: 1: v 1: w 4: 1: v 2: 1: u p 4 3: 1: w p 4 Faulty processes are shown shaded November 2005 Distributed systems: distributed algorithms 173

Consensus & related problems • Impossibility in asynchronous systems – proof: No algorithm exists to reach consensus – No guaranteed solution to • Byzantine generals problem • Interactive consistency • Reliable & totally ordered multicast • Approaches for work around: – Masking faults: restart crashed process and use persistent storage – Use failure detectors: make failure fail-silent by discarding messages November 2005 Distributed systems: distributed algorithms 174

This chapter: overview • • Introduction Logical clocks Global states Failure detectors Mutual exclusion Elections Multicast communication Consensus and related problems November 2005 Distributed systems: distributed algorithms 175

Distributed Systems: Distributed algorithms November 2005 Distributed systems: distributed algorithms 176