Distributed Streams Algorithms for Sliding Windows Phillip B

Distributed Streams Algorithms for Sliding Windows Phillip B. Gibbons, Srikanta Tirthapura 1

Abstract • Algorithm for estimating aggregate functions over a “sliding window” of the N most recent data items in one or more streams. 2

Single stream • The first E-approximation scheme for number of 1’s in a sliding window. • The first E-approximation scheme for the sum of integers in [0. . R] in a sliding window. • Both algorithms are optimal in worst case time and space. • Both algorithms are deterministic 3

Distributed Streams • The first randomized E-approximation scheme for the number of 1’s in a sliding window over the union of distributed streams. 4

Usage • • Network Monitoring Data Warehousing Telecommunications Sensor Networks 5

• Multiple Data Source - Distributed Stream Model • Only the most recent data is important - “Sliding Window” 6

The Goal in the algorithms • Approximating a function F while minimizing : • 1. The total memory • 2. The time take by each party to process a data item • 3. The time to produce an estimate query time 7

Definition 1 An -approximation scheme for a quantity X • A randomized procedure that, given any positive <1 and <1, compute an estimate : • -approximate : An estimate whose worst case relative error is at most 8

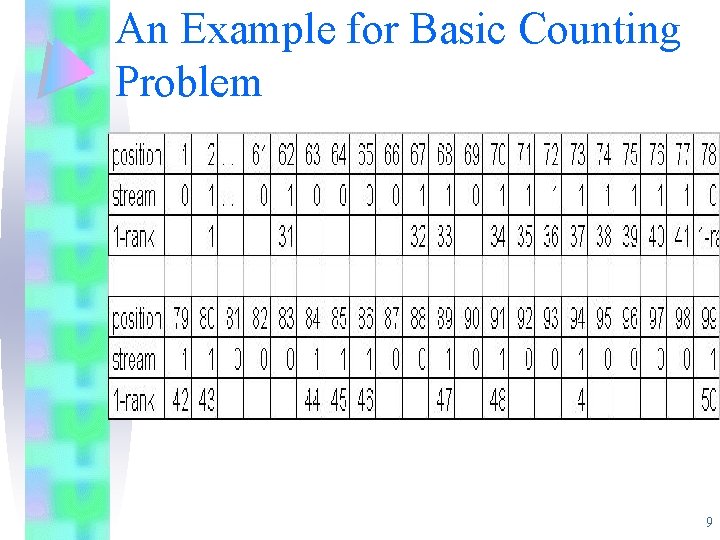
An Example for Basic Counting Problem 9

Algorithms for Distributed Stream • Each party observes only its own stream • Each party communicates with other parties only when estimate is requested • Each party sends a message to a Referee who computes the estimate 10

The Idea • Storing a wave consisting of many random samples of the stream. • Samples that contain only the recent items are sampled at a high probability, while those containing old items are sampled at a lower probability 11

Contributions • Introducing a data structures called waves • Presenting the first E-approximation scheme for Basic Counting. • Presenting the first E-approximation scheme for the sum of integers in [0. . R]. Both optimal in worst case space, processing time and query time. 12

Contributions • Presenting the first randomized -approximation for the number of 1’s in a sliding window over the union of distributed streams 13

Related Work • From the paper of Datar et al : • Using Exponential Histogram data base 14

Exponential Histogram • Maintain more information about recently seen items, less about old items. • k 0 most recent 1’s are assigned to individual bucket • The K 1 next most recent 1’s are assigned to bucket size 2. • The K 2 next most recent 1’s are assigned to bucket size 4. • So on until last N items are assigned to some bucket 15

Exponential Histogram • Each ki is either or • The last bucket is discarded if its position no longer falls within the window • If the new item is a 1, it is assigned to a new bucket of size 1. • If this make , then the two least recent buckets of size 1 are merged to form a bucket of size 2. • If k 1 in now too large, the two least recent buckets of size 2 are merged • So on resulting in a cascading of up to log N bucket merges in the worst case. • The approach using waves avoids this cascading 16

The Basic Wave • Assumption : is an integer. • Counters: 1. pos - the current length of stream 2. rank - the current number of 1’s in the stream. • The wave contains the position of the recent 1’s in the stream, arranged at different “levels”. • For i=1, 2, . . , l-1, level i contains the positions of the most recent 1 bits whose 1 -rank is a multiple of 17

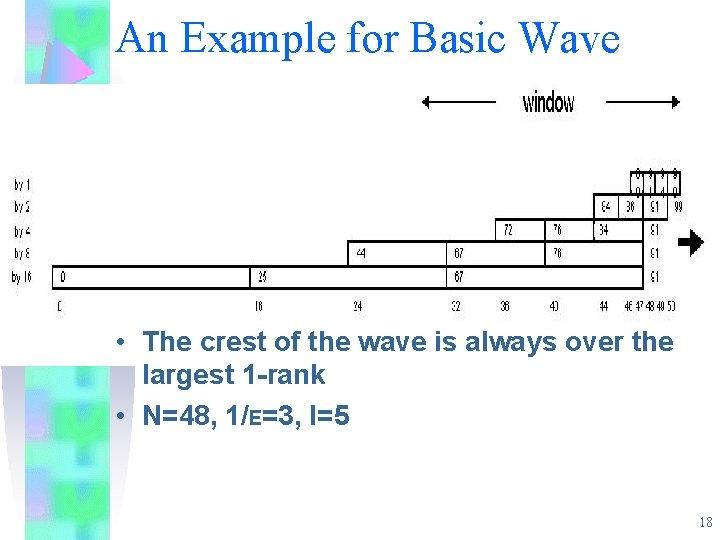
An Example for Basic Wave • The crest of the wave is always over the largest 1 -rank • N=48, 1/E=3, l=5 18

Estimation Steps: • Let s=max(0, pos-n+1) {estimation number of 1’s in [s, pos]} • Let p 1 be the maximum position less than s, and p 2 the minimum position greater/equal then s. • Let r 1 and r 2 be the rank-1 of p 1 and p 2 respectively. • Return = rank-r+1 where r= r 2 if r 2 r 1 =1 otherwise r=(r 1+r 2)/2 19

LEMMA 1 • The procedure returns an estimate that is within a relative error of E of the actual number of 1’s in the window. 20

Proof • Let j be the smallest numbered level containing position p 1. • By returning the midpoint of the range [r 1, r 2] , we guarantee that the absolute error is at most (r 2 r 1)/2 • There is at most a gap between r 1 and its next larger position r 2. • Thus the absolute error in our estimate is at most • Let r 3 be the earliest 1 -rank at level j-1. • r 3> r 1, r 3>=r 2. • by definition 21

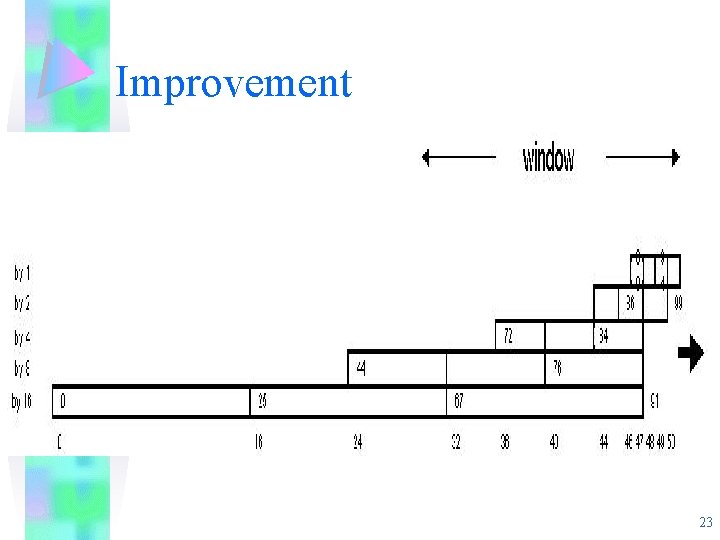
Improvement • Use modulo N’ counters for pos and rank, store the positions in the wave as modulo N’ numbers - Take only log N’ bits. • Keep track of both the largest 1 -rank discarded (r 1) and the smallest 1 rank (r 2) still in the wave - Number of 1’s answer in O(1). • Instead of storing a single position in multiple levels, store each position only at its maximal level. 22

Improvement 23

Improvement • The positions at each level are stored in a fixed length queue so that each time new position is added , the position at the end of the queue is removed. • Maintaining a doubly link list of the position in the wave in increasing order. • By storing the difference between consecutive positions instead of the absolute positions - reduce the space from to 24

The deterministic wave algorithm • Upon receiving a stream bit b: 1. Increment pos (modulo N’=2 N) 2. If the head(p, r) of the linked list L has expired (p<=pos-N), then discard it from L and from its queue, and store r as the largest 1 -rank discarded • 3. If b=1 then do: (a)Increment rank, and determine the corresponding wave level j, the largest j such that rank is a multiple of (b)If the level j queue is full, discard the tail of the queue and splice it out of L (c)Add(pos, rank) to the head of the level j queue and the tail of L 25

Answering a query for a sliding window of size N: • . 1 Let r 1 the largest 1 -rank discarded. (If no such r 1, return rank as exact answer. ) Let r 2 be 1 -rank at the head of the linked list L. (If L is empty, return 0). • 2. Return rank-r+1, where r=r 2 if r 2 -r 1=1 and otherwise r=(r 1+r 2)/2 26

• Space • Process time for each item - O(1) • Estimate time - O(1) • In related work (Datar et al) • Space • Process time for each item - O(log(EN)) 27

Sum of Bounded Integers • The sum over a sliding window can range from 0 to NR. • Let N’ be smallest power of 2 greater than/equal to 2 RN. • Counters(modulo N’): pos - the current length total - the running sum • l=log(2 ENR) levels. • Storing triple for each item (p, v, z) v-the value for the data item z-the partial sum trough this item 28

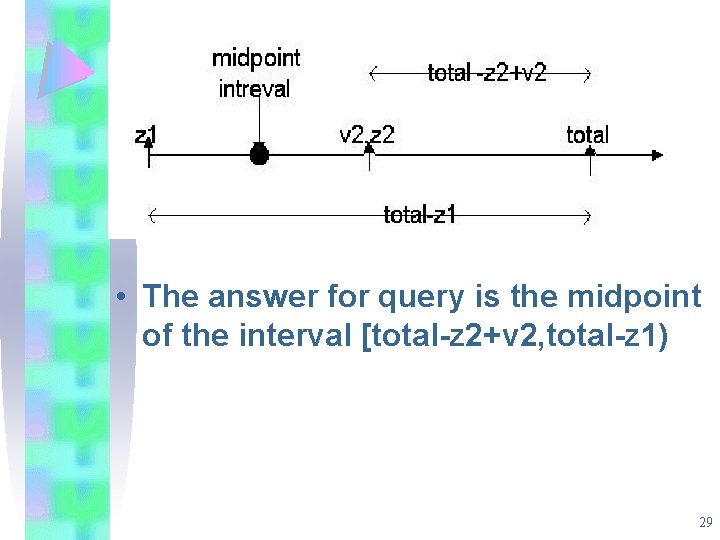
• The answer for query is the midpoint of the interval [total-z 2+v 2, total-z 1) 29

The Algorithm for the sum of last N items in a data stream • Upon receiving a stream value v between 0 to R: • 1. Increment pos (modulo N’=2 N) • 2. If the head(p, v’, z) of the linked list L has expired (p<=pos-N), then discard it from L and from its queue, and store z as the largest partial sum discarded • 3. If v>0 then do: • (a)Determine the largest j such that some number in (total, total+v) is a multiple of Add v to total. • (b)If the level j queue is full, discard the tail of the queue and splice it out of L • (c)Add(pos, v, total) to the head of the level j queue and the tail of L 30

Step 3 a • The desired wave level is the largest position j such that some number y in the interval (total, total+v] has 0’s in all positions less than j. • y-1 and y differ in bit position j. • If bit j changes from 1 to 0 at any point in [total, total+v], then j is not the largest • j is the position of the most-significant bit that is 0 in total and 1 in total+v. • j is the most -significant bit that is 1 in bitwise xor between total and total+v 31

Answering a query for a sliding window of size N : • . 1 Let z 1 be the largest partial sum discarded from L. (If no such z 1, return total as exact answer. ) Let (pos, v 2, z 2) be the head of the linked list L. (If L is empty, return 0). • 2. Return [total - (z 1+z 2 -v 2)/2] 32

• Space -O(1/E(log. N+log. R)) memory word of O(log. N+log. R) • Process time for each item - O(1) • Estimate time - O(1) • In related work (Datar et al) • Space - O(1/E(log. N+log. R)) buckets of log. N+log(log. N+log. R) • Process time for each item - O(log. N+log. R) 33

Distributed Streams • Tree definitions for sliding window over a collection of t>1 distributed stream: 1. Seeking the total number of 1’s in the last N items in each of the t streams (t. N items in total) 2. A single logical stream has been split arbitrarily among the parties. Each party receives items that include a sequence number in the logical stream. Seeking the total number of 1’s in the last N items in the logical stream. 3. Seeking the total number of 1’s in the last N items in the position-wise union of the t streams 34

Solution for First Scenario : • Applying single stream algorithm to each stream. • To answer a query, each party sends its count to the Referee. • The Referee sums the answers. • Because each individual count is within E relative error, so is the total. 35

Solution for Second Scenario : • To answer a query, each party sends its wave to the Referee. • The Referee computes the maximum sequence number over all the parties use each wave to obtain an estimate over the resulting window, and sum the result. • Because each individual count is within E relative error, so is the total. 36

Randomized Waves • Contains the positions of the recent 1’s in the data stream, stored at different levels. • Each level i contains the most recently selected positions of the 1 -bits, where a position is selected into level i with probability • The deterministic wave select 1 out of every 1 -bits at regular interval. • A randomized wave selects an expected 1 out of every 1 -bits random interval. • The randomize wave retains more position per level. 37

The Basic Randomized Wave • • Let N’ be the power of 2 that is at least 2 N Let d=log. N’ Let E<1 be the desired error probability Each Party Pj maintains a basic randomized wave for its stream consisting of d+1 queues, Qj(0), . . , Qj(d), one for each level. • Using a psedo-random hash function h to map positions to levels, according to exponential distribution 38

The Steps for Maintaining the Randomized Wave: • Party Pj, upon receiving a stream bit b: 1. Increment pos (modulo N’=2 N) 2. Discard any position p in the tail of a queue that has expired (p<=pos-N) 3. If b=1 then for l= 0, . . , h(pos) do: (a) If the level l queue Qj(l) is full, then discard the tail of Qj(l) (b) Add pos to the head of Qj(l). • The sample for each level, stored in a queue, contains the most recent position selected into the level. (c=36) 39

• Consider a queue Qj(l) contains all the 1 -bitwise the interval [I, pos] whose position i. Then Qj(l) contains all the 1 -bits in the interval [i, pos] whose positions hash to a value greater than equal to l. • As we move from level l to l+1, the range may increase. • The queues at lower numbered levels may have ranges that fail to contain the window, but as we move to higher levels, we will find a level whose contains the window 40

Answering a query for a sliding window of size n<=N • After each party has observed pos bits: 1. Each party j sends its wave, {Qj(0), . . , Qj(log. N’))}, to the Referee, let s=max(0, pos-n+1). Then W=[s, pos] is the desired window. 2. For j=1, . . , t let lj be the minimum level such that the tail of Qj(lj) is a position p<=s. 3. Let l*=max{lj}, j=0, . . , t. Let U be the union of all positions in Q 1(l*), . . Qt(l*). 4. Return 41

• The algorithm returns an estimate for Union Counting Problem for any sliding window of size n<=N that is within a relative error E with probability greater than 2/3 • space - 42