Distributed Hash Tables and Structured P 2 P

Distributed Hash Tables and Structured P 2 P Systems Ningfang Mi September 27, 2004 1

Outline l The Lookup problem ¡ ¡ ¡ l Case study: CAN ¡ ¡ l Definition Approaches Issues Overview Basic design More design improvements (Performance, robustness) Topology-aware routing in CAN Conclusion 2

The Lookup Problem -- Definition l Given a data item X stored at some dynamic set of nodes, find it l It is an important and critical common problem in P 2 P. l How to efficiently find it? 3

The Lookup Problem -- Approaches l Central database: Napster ¡ l Use hierarchy: DNS for name lookup ¡ ¡ l ¡ No more important node “Flooding” request not scale well “Superpeers” in a hierarchical structure: Ka. Za. A ¡ l Failure or removal of the root or nodes high in hierarchy overload Symmetric lookup algorithm: Gnutella ¡ l Central point of failure Failure of “Superpeers” Innovative symmetric lookup strategy: Freenet ¡ Need visit large number of nodes and no guarantee 4

The Lookup Problem -- Approaches l Structured and symmetric algorithms: ¡ Implement the DHT (distributed hash table) Convert name to key using a hash function, SHA-1 l One operation: Lookup(key) l ¡ Examples: CAN[2] -- ACM SIGCOMM 2001 l Chord[3] -- ACM SIGCOMM 2001 l Pastry[5] -- Middleware 2001 l Tapestry[6] – UC Berkeley 2001 l 5

The Lookup Problem -- Issues l Mapping keys to nodes in a load balanced way l Forwarding a lookup for a key to an appropriate node l Distance function l Building routing tables adaptively Discuss these issues by a case study -- CAN 6

“What is a scalable content-addressable network”? ? ? --- CANs Design Overview l Features: ¡ Completely distributed system l ¡ Scalable l l ¡ Maintain only a small number of control states Independent of the number of nodes content-addressable l ¡ No centralized control, coordination and configuration Resembling a hash table: keys values Fault-tolerant l Can route around failures 7

“How does a scalable CAN work” ? ? ? --- CANs Design Overview l Using a virtual d-dimensional Cartesian coordinate space ¡ l CAN is composed of individual nodes ¡ ¡ l l Zone: hyper-rectangles Each node “owns” its individual, distinct zone Each node “holds” state information about its neighbor zones Three operations ¡ insertion, lookup and deletion ¡ (key, value) Requests for a key are routed by using a greedy routing algorithm 8

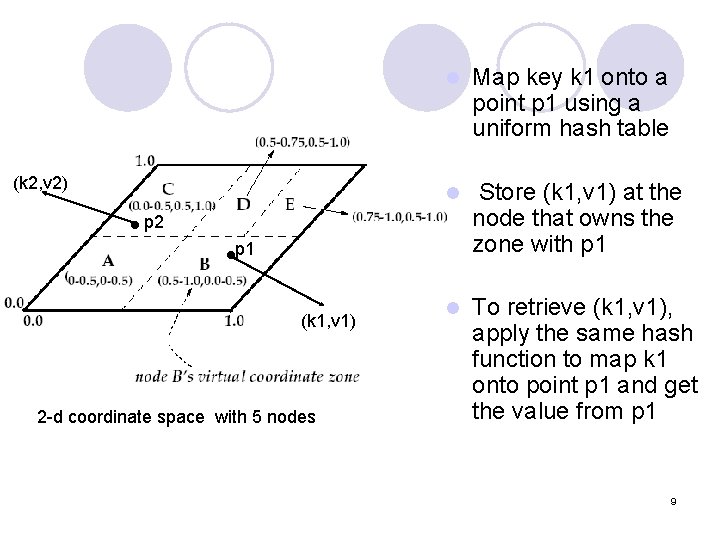
(k 2, v 2) l Map key k 1 onto a point p 1 using a uniform hash table l Store (k 1, v 1) at the node that owns the zone with p 1 l To retrieve (k 1, v 1), apply the same hash function to map k 1 onto point p 1 and get the value from p 1 p 2 p 1 (k 1, v 1) 2 -d coordinate space with 5 nodes 9

Basic design for a CAN l CAN routing l Construction of the CAN overlay l Maintenance of the CAN overlay Three most basic pieces of the design. 10

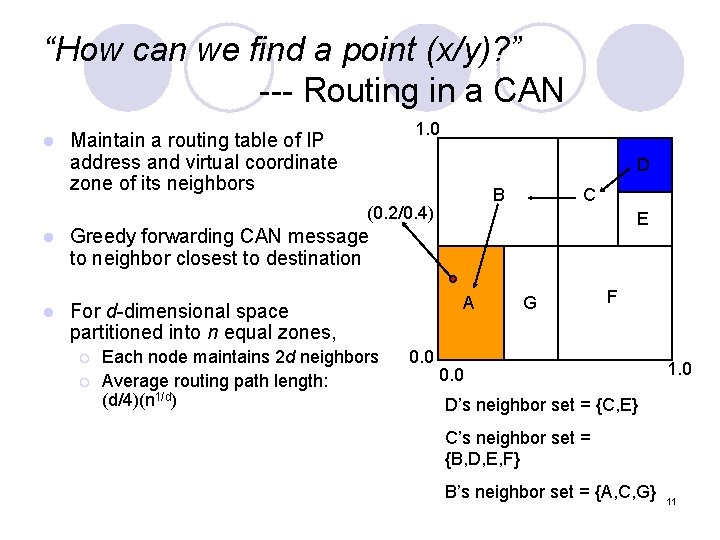
“How can we find a point (x/y)? ” --- Routing in a CAN l 1. 0 Maintain a routing table of IP address and virtual coordinate zone of its neighbors D B (0. 2/0. 4) l l C E Greedy forwarding CAN message to neighbor closest to destination A For d-dimensional space partitioned into n equal zones, ¡ ¡ Each node maintains 2 d neighbors Average routing path length: (d/4)(n 1/d) 0. 0 G F 0. 0 1. 0 D’s neighbor set = {C, E} C’s neighbor set = {B, D, E, F} B’s neighbor set = {A, C, G} 11

“I want to join!” --- CAN Construction l Find a node already in the CAN ¡ ¡ l Finding a zone in the space ¡ ¡ ¡ l Retrieve a bootstrap node’s IP address by looking up the CAN domain name in DNS Bootstrap node provides IP addresses of random nodes in CAN Randomly choose a point in the space Send “JOIN” request to P via an exiting CAN node A Node B in zone with P splits the zone and allocates “half” with (key, value) pairs to new node Joining the routing by notifying the neighbors ¡ ¡ ¡ Learn IP addresses of its neighbors set from previous occupant Previous occupant updates its neighbor set New and old neighbors be informed of this reallocation. 12

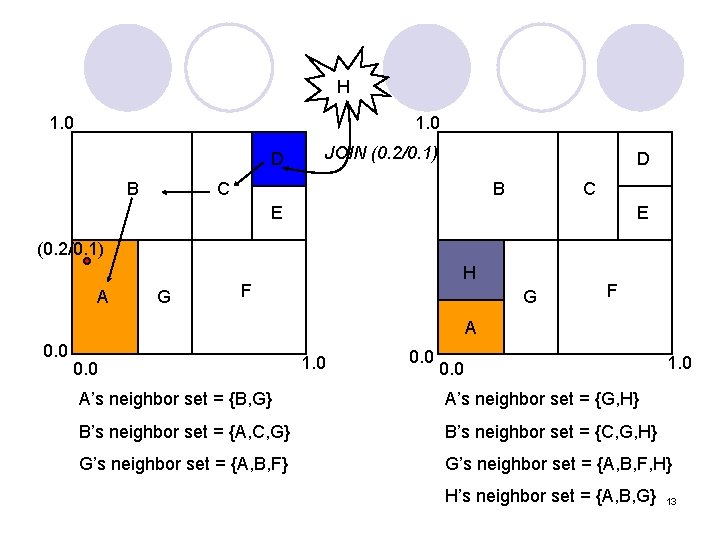
H 1. 0 D B JOIN (0. 2/0. 1) D C B C E E (0. 2/0. 1) A G H F G F A 0. 0 1. 0 A’s neighbor set = {B, G} A’s neighbor set = {G, H} B’s neighbor set = {A, C, G} B’s neighbor set = {C, G, H} G’s neighbor set = {A, B, F, H} H’s neighbor set = {A, B, G} 13

“I want to leave!” --- CAN Maintenance Zone must be taken over by some node l Normal procedure l ¡ ¡ l Explicitly hand over zone and (key, value) pairs to one neighbor Merge to valid zone if possible, otherwise the neighbor with smallest zone handle both zones temporarily Failure: immediate takeover algorithm ¡ ¡ Neighbors initialize takeover timers Alive Neighbor with smallest zone takes over zone 14

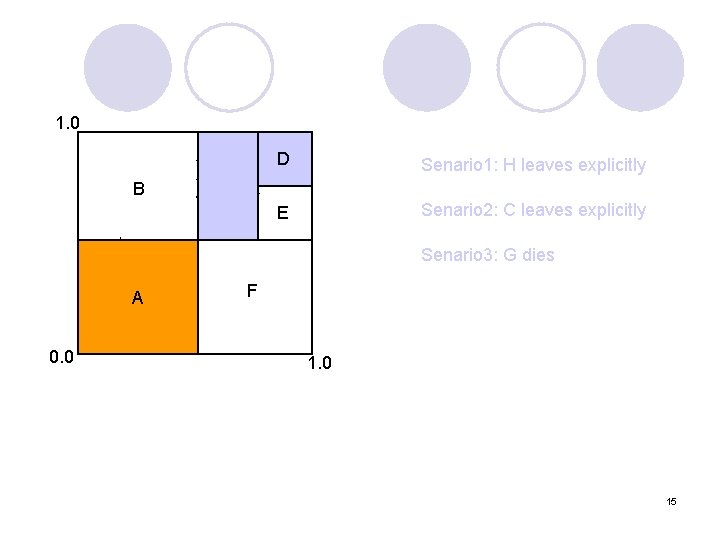
1. 0 B H A A D Senario 1: H leaves explicitly E Senario 2: C leaves explicitly C Senario 3: G dies G F A 0. 0 15

“Can we do Better? ? ? ” --- Design Improvements (1) l Basic design ¡ Balance low per-node state (O(d)) and short path lengths (O(dn 1/d)) ¡ Application level hops, not IP level hops ¡ Neighbor nodes may be geographically distant with many IP hops l Average total latency of a look up == Avg(# of CAN hops) X Avg(latency of each CAN hop) 16

“Can we do Better? ? ? ” --- Design Improvements (2) l Primary goal: ¡ Reduce the latency of CAN routing l l l Other achievements ¡ ¡ l Path length Per-CAN-hop latency Robustness– routing & data availability Load balancing Simulated CAN design on Transit-Stub (TS) topologies using the GT-ITM topology generator 17

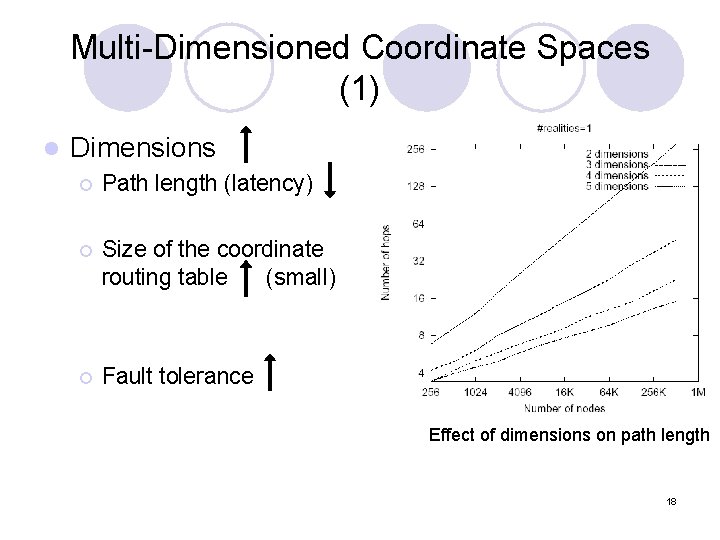
Multi-Dimensioned Coordinate Spaces (1) l Dimensions ¡ Path length (latency) ¡ Size of the coordinate routing table (small) ¡ Fault tolerance Effect of dimensions on path length 18

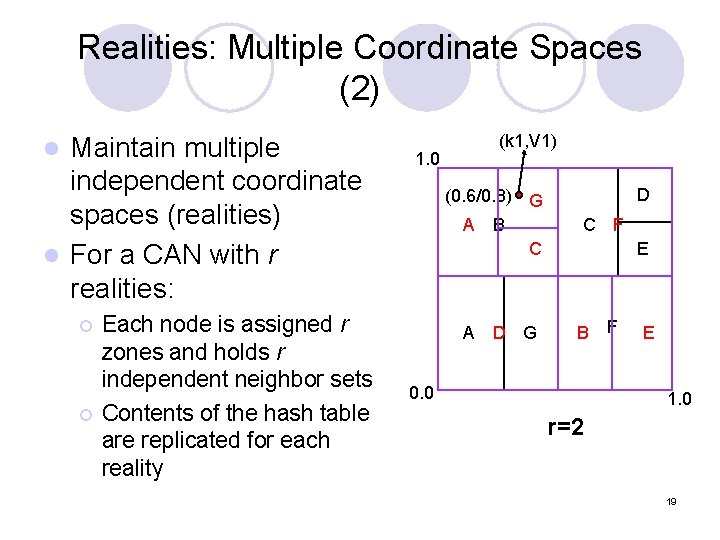
Realities: Multiple Coordinate Spaces (2) Maintain multiple independent coordinate spaces (realities) l For a CAN with r realities: l ¡ ¡ Each node is assigned r zones and holds r independent neighbor sets Contents of the hash table are replicated for each reality (k 1, V 1) 1. 0 (0. 6/0. 8) G A B C A D G D C F E B 0. 0 F E 1. 0 r=2 19

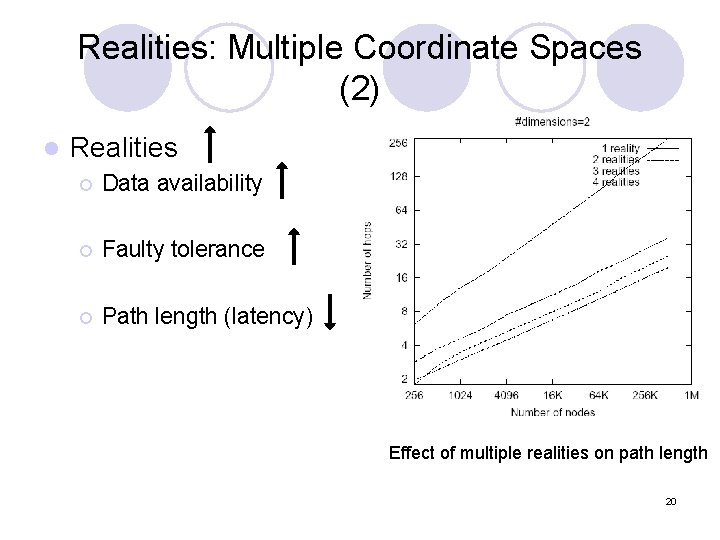
Realities: Multiple Coordinate Spaces (2) l Realities ¡ Data availability ¡ Faulty tolerance ¡ Path length (latency) Effect of multiple realities on path length 20

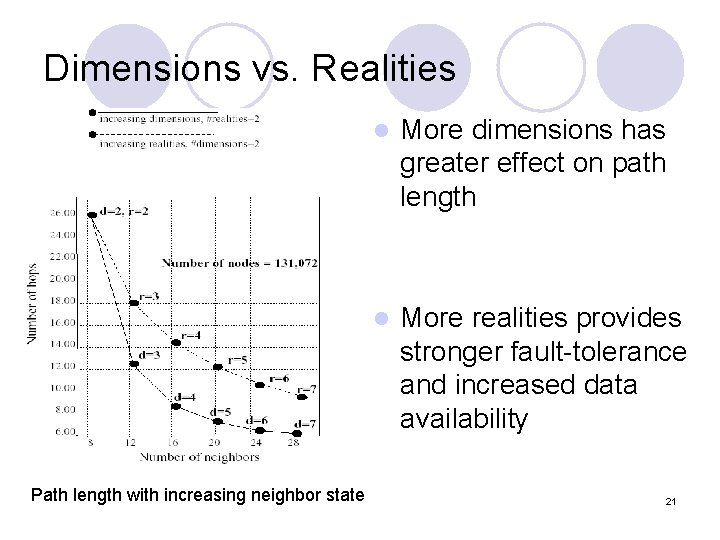
Dimensions vs. Realities Path length with increasing neighbor state l More dimensions has greater effect on path length l More realities provides stronger fault-tolerance and increased data availability 21

Better CAN Routing Metrics (3) l (Basic CAN routing metric: ¡ l Cartesian distance in virtual coordinate space) RTT-weighted routing (round-trip-time) ¡ ¡ Reflect underlying IP topology Each node measures RTT to each neighbor Forward message to neighbor with maximum ratio of progress to RTT Reduce the latency of individual hops 22

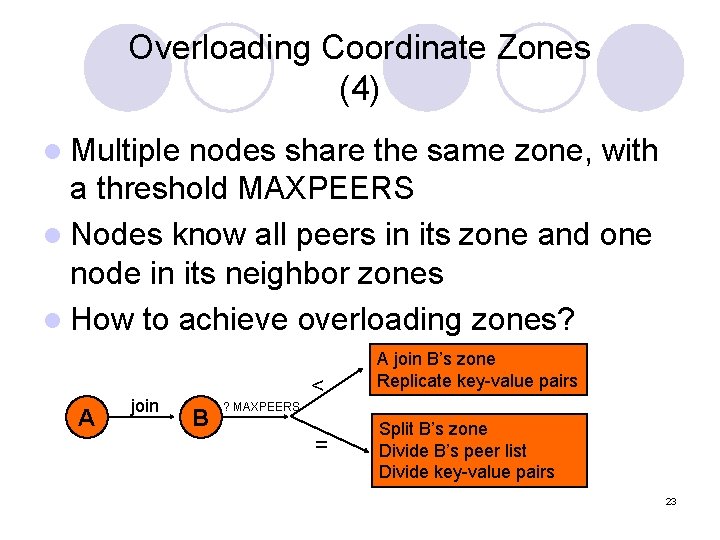
Overloading Coordinate Zones (4) l Multiple nodes share the same zone, with a threshold MAXPEERS l Nodes know all peers in its zone and one node in its neighbor zones l How to achieve overloading zones? A join < B A join B’s zone Replicate key-value pairs ? MAXPEERS = Split B’s zone Divide B’s peer list Divide key-value pairs 23

Overloading Coordinate Zones (4) l Advantage: ¡ ¡ ¡ l Reduce path length (number of hops) Reduce per-hop latency Improve fault tolerance Disadvantage: ¡ Add somewhat to system complexity 24

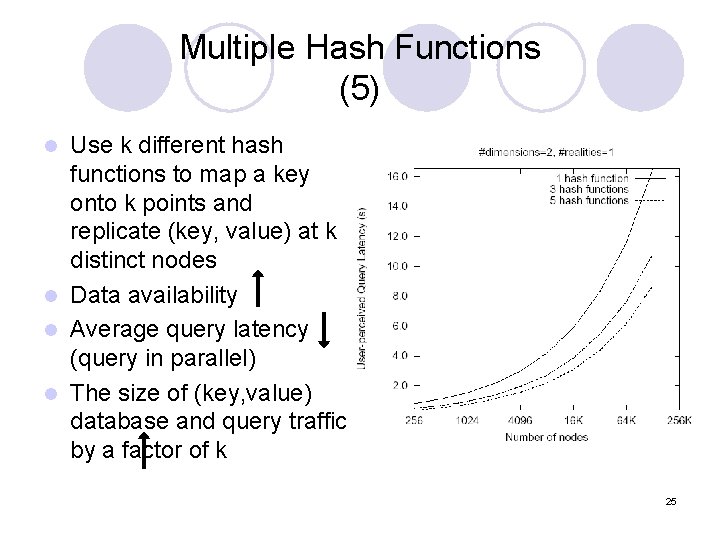
Multiple Hash Functions (5) Use k different hash functions to map a key onto k points and replicate (key, value) at k distinct nodes l Data availability l Average query latency (query in parallel) l The size of (key, value) database and query traffic by a factor of k l 25

Topologically-Sensitive Construction of the CAN Overlay Network (6) l Problem of randomly allocating nodes to zones ¡ Strange routing scenario inefficient routing Goal: construct CAN overlay that are congruent with the underlying IP topology l Landmarks: a well-known set of machines like DNS servers l Each node measures its RTT to each landmark l ¡ ¡ Order each landmark in order of increasing RTT For m landmarks: m! possible orderings Partition coordinate space into m! equal size partitions l Nodes join CAN at random point in the partition corresponding to its landmark ordering l 26

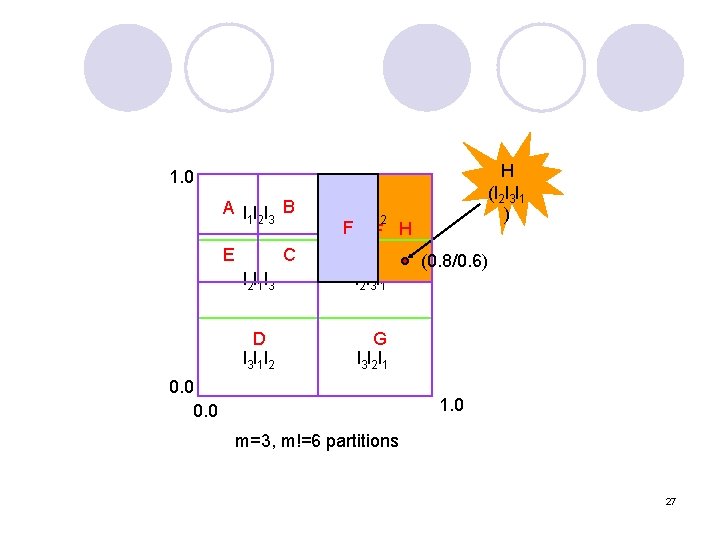
H (l 2 l 3 l 1 ) 1. 0 A lll B 123 E l 1 l 3 l 2 F F H C l 2 l 1 l 3 l 2 l 3 l 1 D l 3 l 1 l 2 G l 3 l 2 l 1 0. 0 (0. 8/0. 6) 1. 0 m=3, m!=6 partitions 27

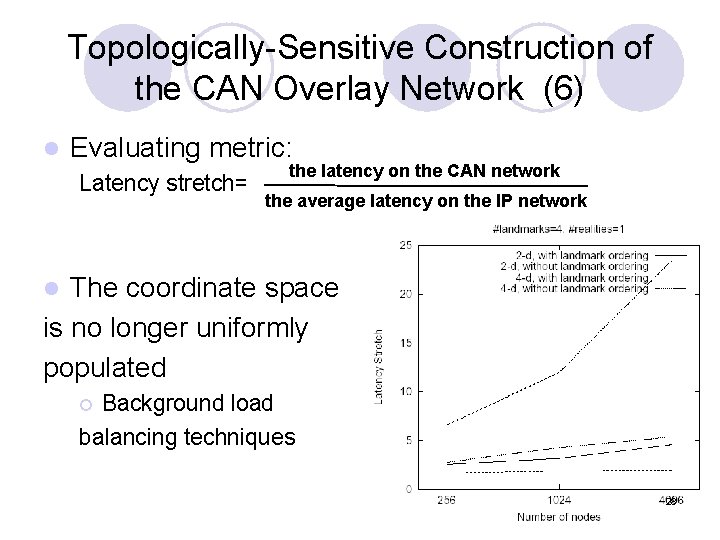
Topologically-Sensitive Construction of the CAN Overlay Network (6) l Evaluating metric: Latency stretch= the latency on the CAN network the average latency on the IP network The coordinate space is no longer uniformly populated l Background load balancing techniques ¡ 28

Load Balancing Techniques (7) l More uniform partitioning-- volume balancing ¡ ¡ ¡ l When “JOIN” is received, compare its own zone volume with neighbors’ zone volumes Split zone with largest volume Results: V=VT/n, VT is the total volume Type % of nodes with volume V Largest Volume without 40% 8 V with 90% 4 V Catching and replication for “hot spot” ¡ ¡ Catch the data keys it recently accessed Replicate the “hot” data key at its neighboring nodes 29

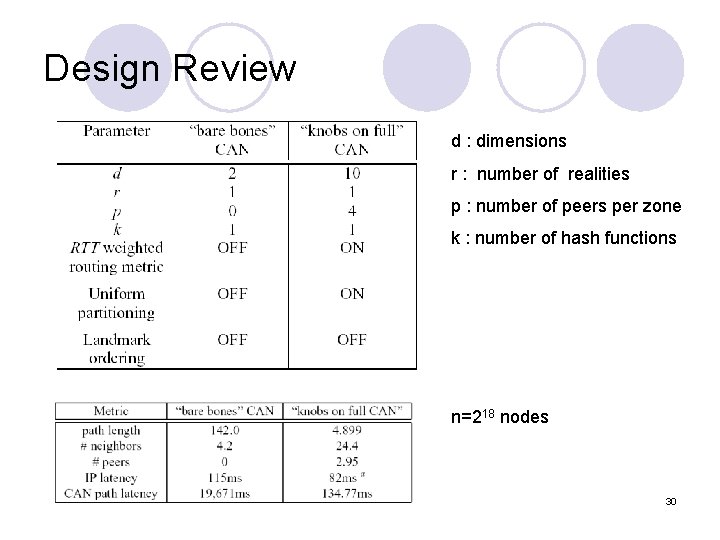
Design Review d : dimensions r : number of realities p : number of peers per zone k : number of hash functions n=218 nodes 30

Topology-Aware Routing in CAN l “It is critical for overlay routing to be aware of the network topology” [6] 31

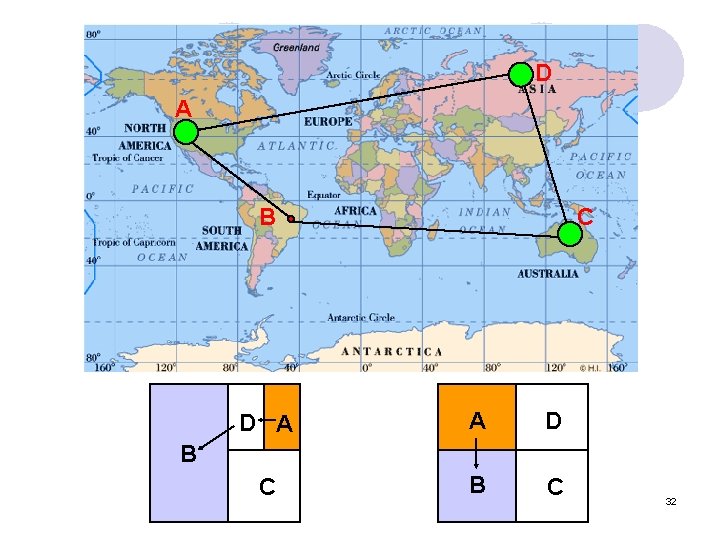
D A B C D A A D C B 32

Approaches to Topology-Aware Routing in CAN l Proximity routing l Topology-based node. Id assignment l Proximity ¡ Doesn’t neighbor selection work on CAN 33

Proximity Routing l The overlay is constructed without regard for the physical network topology l Among a set of possible next hops, select the one that is ¡ Closest in the physical network ¡ Represents a good compromise between progress in the id space and proximity l Example ¡ Better CAN routing metrics --- RTT 34

Topology-based Node. Id Assignment l Map the overlay’s logical id space onto the physical network l Example 1: Landmark binning [5][7] ¡ Destroy the uniform population of id space ¡ Landmark sites can become overloaded. ¡ Coarse-grained and difficult to distinguish relatively close nodes l Example 2: SAT-match [8] 35

Self-Adaptive Topology (SAT) Matching l Two phases: ¡ ¡ The probing phase: probe nearby nodes for distance measurements as soon as join the system The jumping phase: pick the closest zone accordingly to jump to The iterative process completes until it is close enough to the zone where all its physically close neighbors are located l A global topology matching optimization is achieved. l 36

SAT-Matching -- Probing Phase (1) Effective flooding: flooding with a low number of TTL hops is highly effective, with produce few redundant messages. l Having joined the system based on a DHT assignment, source node floods a message to its neighbors l ¡ l (source IP address, source timestamp, small TTL k) Node that receives message responds to the source with its IP address and flood to its neighbors with k-1 if k-1>0 37

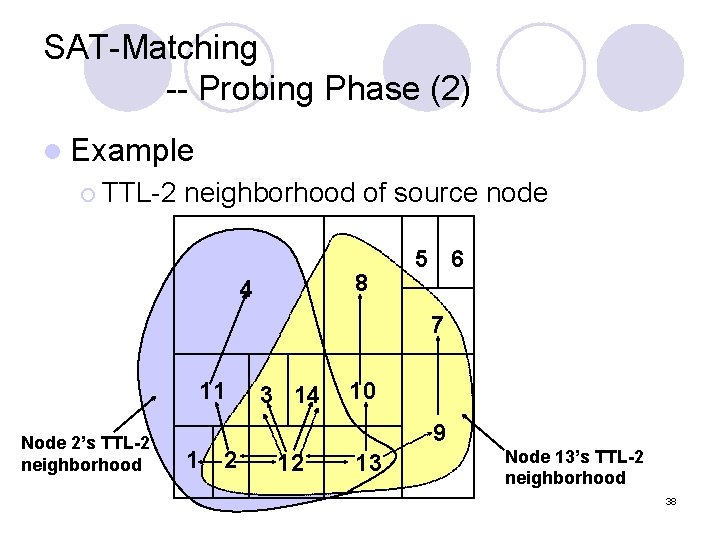
SAT-Matching -- Probing Phase (2) l Example ¡ TTL-2 neighborhood of source node 8 4 5 6 7 11 Node 2’s TTL-2 neighborhood 3 14 10 9 1 2 12 13 Node 13’s TTL-2 neighborhood 38

SAT-Matching -- Probing Phase (3) l After collecting a list of IP address, source node uses a ping facility to measure the RTTs (Round-Trip-Times) to each node that has responded. l Sort these RTTs and select two nodes with the smallest RTTs. l Select one zone associated with one of the two nodes to jump in. 39

SAT-Matching -- Jumping Phase If simply jumping to the zone, the stretch reduction could be offset by latency increases from other new connection. l Jumping criteria: l ¡ l only when the local stretch of the source’s and the sink’s (two closest nodes) TTL-1 neighborhoods is reduced How to jump? (X Y) X return its zone and (key, value) pairs to its neighbor ¡ Y allocate half of its zone and pairs to X ¡ 40

Discussion l Is there way to make structured P 2 P more practical? ¡ It is not free for peers. In CAN, peers are required to follow the protocol and be responsible for some data keys. ¡ Only key search l Can the topology-aware routing be a costeffective manner in a highly dynamic environment? 41

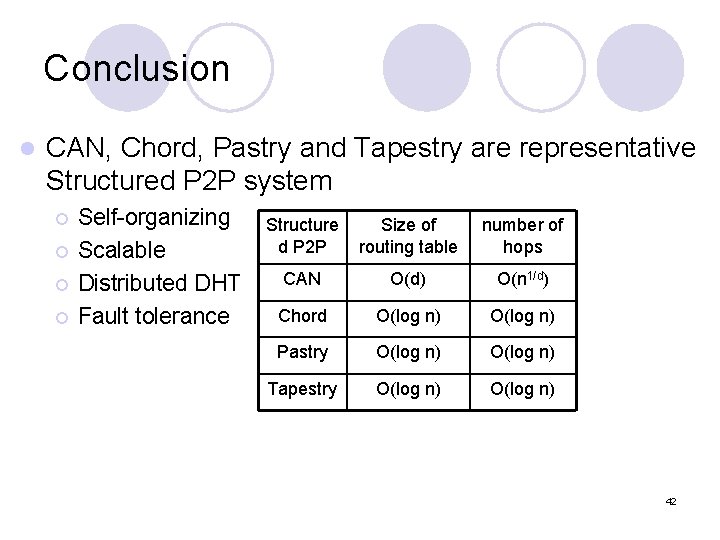
Conclusion l CAN, Chord, Pastry and Tapestry are representative Structured P 2 P system ¡ ¡ Self-organizing Scalable Distributed DHT Fault tolerance Structure d P 2 P Size of routing table number of hops CAN O(d) O(n 1/d) Chord O(log n) Pastry O(log n) Tapestry O(log n) 42

Reference l l l l [1]Hari Balakrishnan, et. , al. , “Looking Up Data in P 2 P Systems”, Communication of the ACM, Vol. 46, N. 2, 2003. [2] Sylvia Ratnasamy, Paul Francis, Mark Handley, and Richard Karp, “A Scalable Content-Addressable Network”, ACM SIGCOMM 2001. [3] Ion Stoica, Robert Morris, David Karger, M. Frans Kaashoek, and Hari Balakrishnan, “Chord: A Scalable Peer-to-peer Lookup Service for Internet Applications”, ACM SIGCOMM 2001. [4]Antony Rowstron and Peter Druschel, “Pastry: Scalable, decentralized object location and routing for large-scale peer-to-peer systems”, Middleware 2001. [5] B. Zhao and J. Kubiatowicz and A. Joseph, “Tapestry: An infrastructure for faulttolerant wide-area location and routing”, U. C. Berkeley, 2001 [6] M. Castro, P. Druschel, Y. C. Hu, and A. Rowstron, "Topologyaware routing in structured peer-to-peer overlay networks“, presented at Intl. Workshop on Future Directions in Distributed Computing, June 2002. [7] S. Ratnasamy, M. Handley, R. Karp, and S. Shenker, “Topologically-aware overlay construction and server selection”, INFOCOM 2002. [8] Shansi Ren, Lei Guo, Song Jiang, and Xiaodong Zhang, “SAT-Match: a selfadaptive topology matching method to achieve low lookup latency in structured P 2 P overlay networks" , Proceedings of the 18 th International Parallel and Distributed Processing Symposium (IPDPS'04), April 26 -30, 2004. 43