Distributed Databases architecture fragmentation allocation Lecture 1 1

Distributed Databases architecture, fragmentation, allocation Lecture 1 1

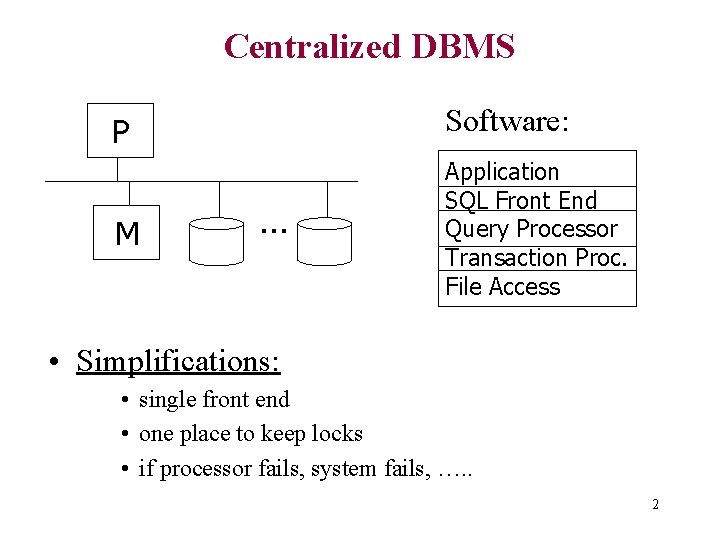
Centralized DBMS P Software: M Application SQL Front End Query Processor Transaction Proc. File Access . . . • Simplifications: • single front end • one place to keep locks • if processor fails, system fails, …. . 2

Distributed DB • Multiple processors, memories, and disks – Opportunity for parallelism (+) – Opportunity for enhanced reliability (+) – Synchronization issues (-) • Heterogeneity and autonomy of “components” – Autonomy example: may not get statistics for query optimization from a site 3

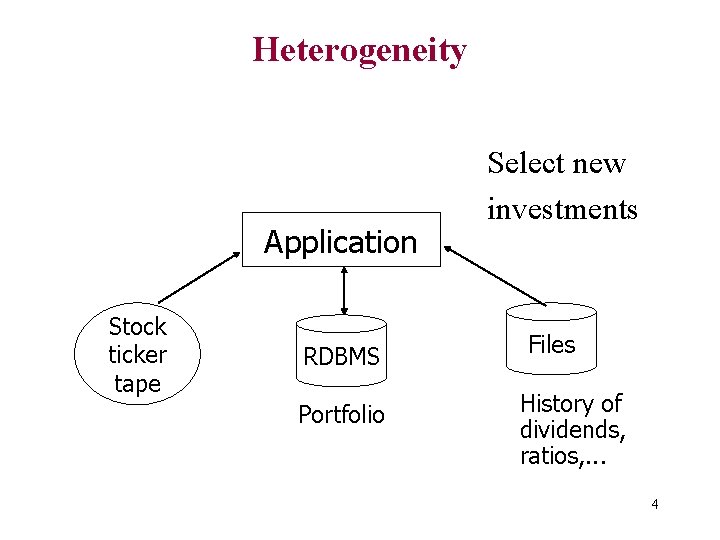
Heterogeneity Application Stock ticker tape RDBMS Portfolio Select new investments Files History of dividends, ratios, . . . 4

Big Picture Data management with multiple processors and possible autonomy, heterogeneity. Impacts: • Data organization • Query processing • Access structures • Concurrency control • Recovery 5

Outline • Introductory topics – Database architectures – Distributed versus Parallel DB systems • Distributed database design – Fragmentation – Allocation 6

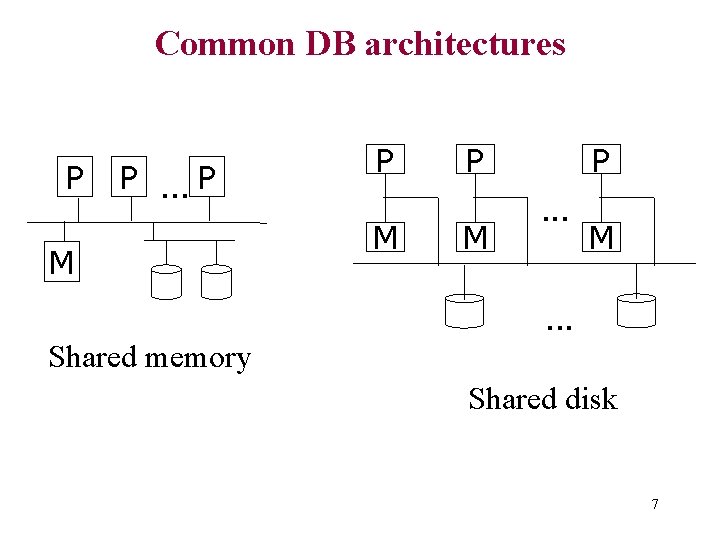
Common DB architectures P P. . . P M P M P. . . M . . . Shared memory Shared disk 7

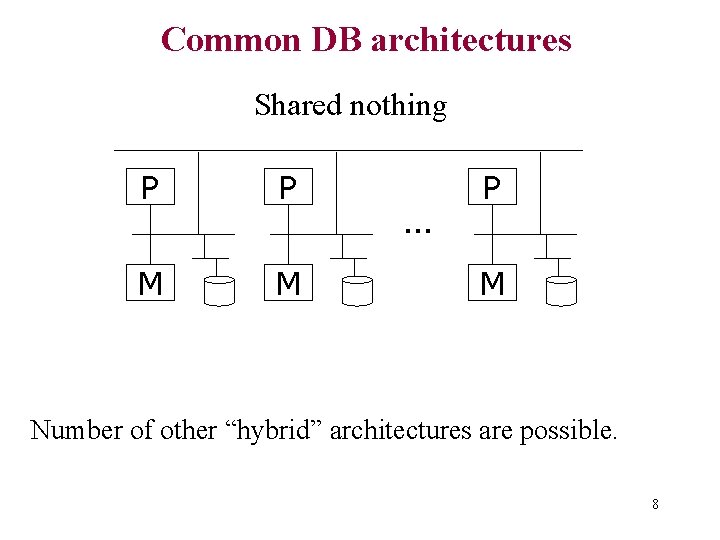
Common DB architectures Shared nothing P P M M . . . P M Number of other “hybrid” architectures are possible. 8

Selecting the “right” architecture • • • Reliability Scalability Geographic distribution of data Performance Cost 9

Parallel vs. Distributed DB system • Typically, parallel DBs: – Fast interconnect – Homogeneous software – Goals: High performance and Transparency • Typically, distributed DBs: – Geographically distributed – Disconnected operation possible – Goal: Data sharing (heterogeneity, autonomy) 10

Typical query processing scenarios • Parallel DB: – Distribute/partition/sort…. data to make certain DB operations (e. g. , Join) fast • Distributed DB: – Given data distribution, find query processing strategy to minimize cost (e. g. communication cost) 11

Distributed DB Design Top-down approach: • have a database • how to split and allocate to individual sites Multi-databases (or bottom-up): • combine existing databases • how to deal with heterogeneity & autonomy 12

Two issues in top-down design • Fragmentation • Allocation Note: issues not independent, but studied separately for simplicity. 13

Example Employee relation E (#, name, loc, sal, …) 40% of queries: Qa: select * Qb: select * from E where loc=Sa where loc=Sb and… and. . . Motivation: Two sites: Sa, Sb Qa Sa Sb Qb 14

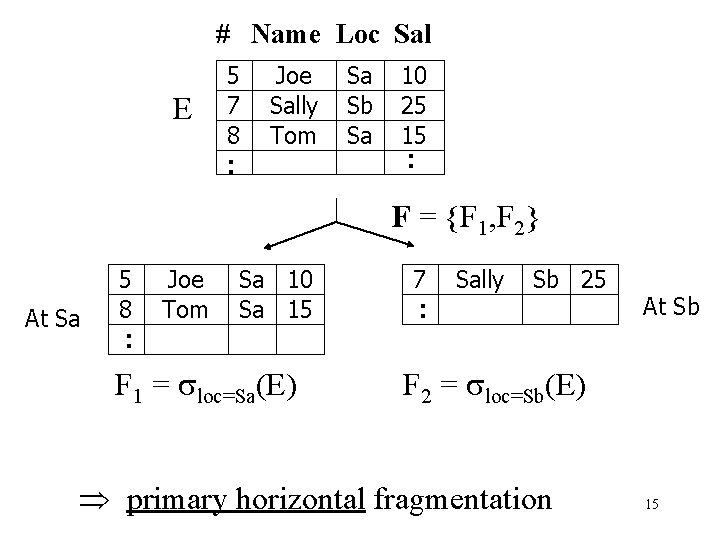
# Name Loc Sal . . E Joe Sally Tom Sa Sb Sa 10 25 15 . . 5 7 8 F = {F 1, F 2} Sa 10 Sa 15 7 Sally Sb 25 . . Joe Tom At Sb . . At Sa 5 8 F 1 = loc=Sa(E) F 2 = loc=Sb(E) primary horizontal fragmentation 15

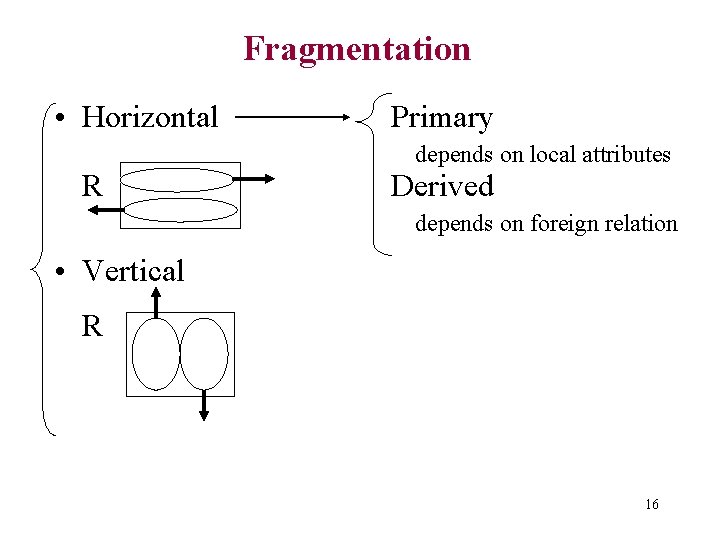
Fragmentation • Horizontal Primary depends on local attributes R Derived depends on foreign relation • Vertical R 16

Horizontal partitioning techniques • Round robin • Hash partitioning • Range partitioning 17

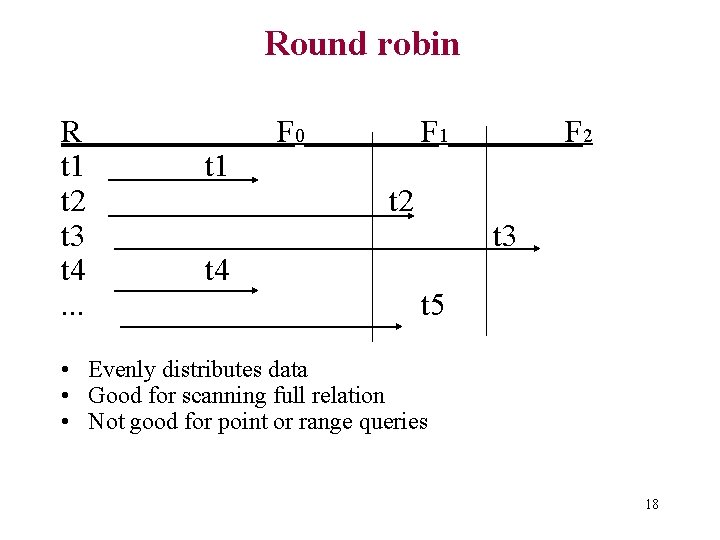
Round robin R t 1 t 2 t 3 t 4. . . t 1 t 4 F 0 F 1 t 2 F 2 t 3 t 5 • Evenly distributes data • Good for scanning full relation • Not good for point or range queries 18

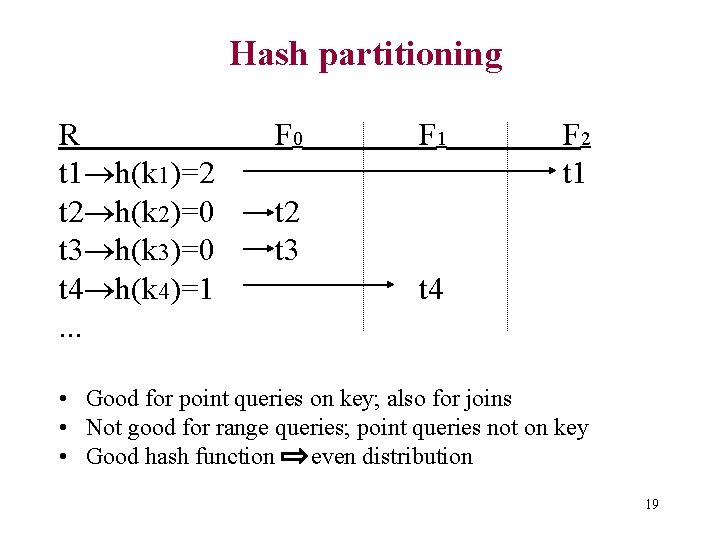
Hash partitioning R t 1 h(k 1)=2 t 2 h(k 2)=0 t 3 h(k 3)=0 t 4 h(k 4)=1. . . F 0 F 1 F 2 t 1 t 2 t 3 t 4 • Good for point queries on key; also for joins • Not good for range queries; point queries not on key • Good hash function even distribution 19

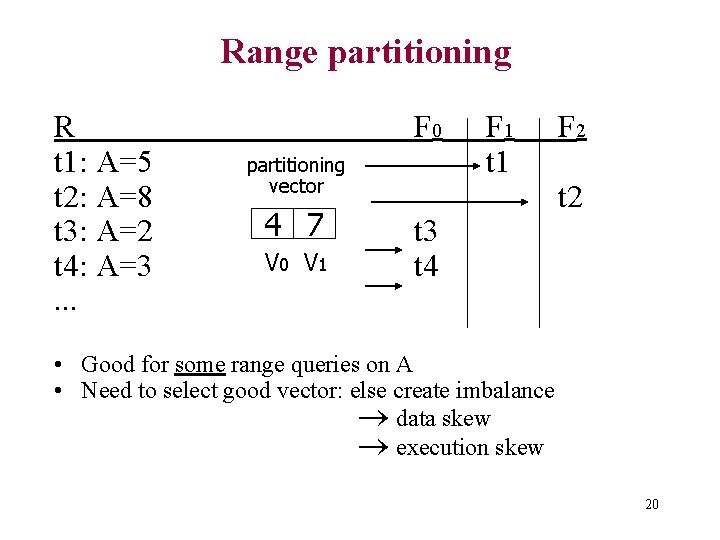
Range partitioning R t 1: A=5 t 2: A=8 t 3: A=2 t 4: A=3. . . F 0 partitioning vector 4 7 V 0 V 1 F 1 t 3 t 4 F 2 t 2 • Good for some range queries on A • Need to select good vector: else create imbalance data skew execution skew 20

Which are good fragmentations? Example 1: F = {F 1, F 2} F 1 = sal<10(E) F 2 = sal>20(E) Problem: Some tuples lost! Example 2: F = {F 3, F 4} F 1 = sal<10(E) F 2 = sal>5(E) Tuples with 5 < sal < 10 are duplicated 21

Prefer to deal with replication explicitly Example: F = { F 5, F 6, F 7 } F 5 = sal<=5(E) F 6 = 5 < sal<10(E) F 7 = sal>=10(E) Then replicate F 6 if desired as part of allocation 22

Horizontal Fragmentation Desiderata R F = {F 1, F 2, …. } (1) Completeness t R, Fi F such that t Fi (2) Disjointness Fi Fj = Ø, i, j such that i j (3) Reconstruction i such that R = Fi 23

Generating horizontal fragments • Given simple predicates Pr = {p 1, p 2, . . pm} and relation R. • Generate “minterm” predicates M = {m | m = pk*, 1 k m}, where pk* is either pk or ¬ pk • Eliminate useless minterms and simplify M to get M’. • Generate fragments m(R) for each m M’. 24

5 < A < 10 Example • Example: say queries use predicates A < 10, A > 5, Loc = SA, Loc = SB • Eliminate and simplify minterms A < 10 A > 5 Loc = SA Loc = SB A < 10 A > 5 Loc = SA ¬(Loc = SB) • Final set of fragments (5 < A < 10) (Loc = SA) (5 < A < 10) (Loc = SB) (A 5) (Loc = SA) (A 5) (Loc = SB) (A 10) (Loc = SA) (A 10) (Loc = SB) Work out details for all minterms. 25

More on Horizontal Fragmentation • Elimination of useless fragments/predicates depends on application semantics: – e. g. : if Loc SA and SB is possible, must retain fragments such as (5 <A < 10) (Loc SA) (Loc SB) • Minterm-based fragmentation generates complete, disjoint, and reconstructible fragments. Justify this statement. 26

Choosing simple predicates • E (#, name, loc, sal, …) with common queries Qa: select * from E where loc = SA and… Qb: select * from E where loc = SB and… Qc: select * from E where sal < 10 and… • Three choices for Pr and hence F[Pr]: – Pr = {} F 1 = F[Pr] = {E} – Pr = {Loc = SA, Loc = SB} F 2 = F[Pr] = { loc=SA (E), loc=SB (E)} – Pr = {Loc = SA, Loc = SB, Sal < 10} F 3 = F[Pr] = { loc=SA sal< 10(E), loc=SB sal< 10(E), loc=SA sal 10 (E)} 27

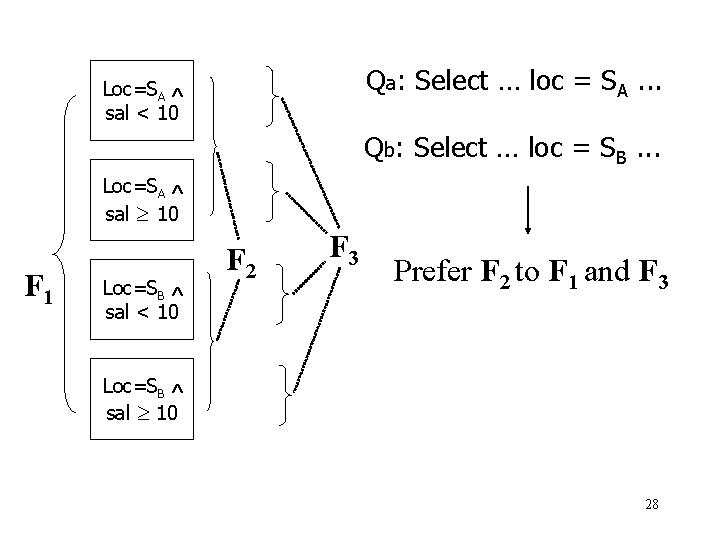
Qa: Select … loc = SA. . . Loc=SA sal < 10 Qb: Select … loc = SB. . . Loc=SA sal 10 F 1 Loc=SB sal < 10 F 2 F 3 Prefer F 2 to F 1 and F 3 Loc=SB sal 10 28

Desiderata for simple predicates Different from completeness of fragmentation • Completeness Set of predicates Pr is complete if for every Fi F[Pr], every t Fi has equal probability of access by every major application. • Minimality Set of predicates Pr is minimal if no Pr’ Pr is complete. To get complete and minimal Pr use predicates that are 29 “relevant” in frequent queries

Derived horizontal fragmentation • Example: Two relations Employee and Jobs E(#, NAME, SAL, LOC) J(#, DES, …) • Fragment E into {E 1, E 2} by LOC • Common query: “Given employee name, list projects (s)he works in” 30

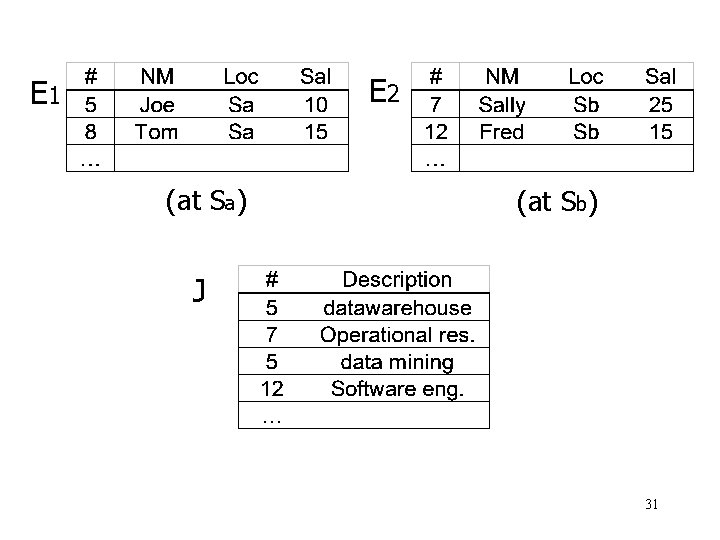
E 2 E 1 (at Sa) (at Sb) J 31

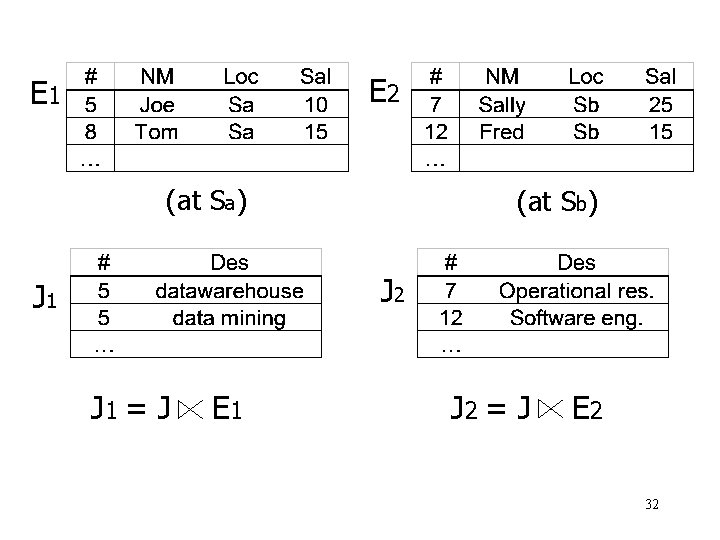
E 2 E 1 (at Sa) (at Sb) J 2 J 1 = J E 1 J 2 = J E 2 32

Derived horizontal fragmentation R, fragmented as F = {F 1, F 2, …, Fn} S, derive D = {D 1, D 2, …, Dn} where Di =S Fi Convention: R is called the owner relation S is called the member relation 33

Completeness of derived fragmentation Example: Say J is • J 1 U J 2 J (incomplete fragmentation) • For completeness, enforce referential integrity constraint join attribute of member relation joint attribute of owner relation 34

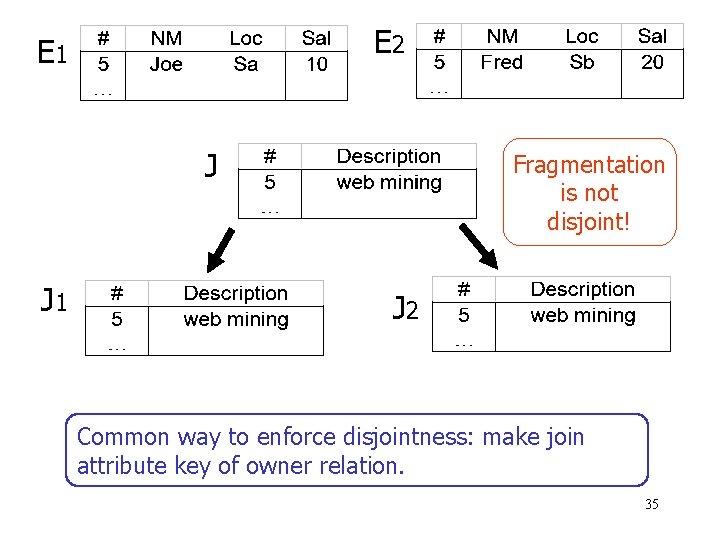
E 2 E 1 J J 1 Fragmentation is not disjoint! J 2 Common way to enforce disjointness: make join attribute key of owner relation. 35

Vertical fragmentation Example: E 1 E E 2 R[T] R 1[T 1], R 2[T 2], …, Rn[Tn] Just like normalization of relations Ti T 36

Properties R[T] Ri[Ti], i = 1. . n • Completeness: • Reconstruction: T i = T Ri = R (lossless join) – One way to guarantee lossless join: repeat key in each fragment, i. e. , key Ti i • Disjointness: Ti Tj = {key} – Check disjointness only on non-key attributes 37

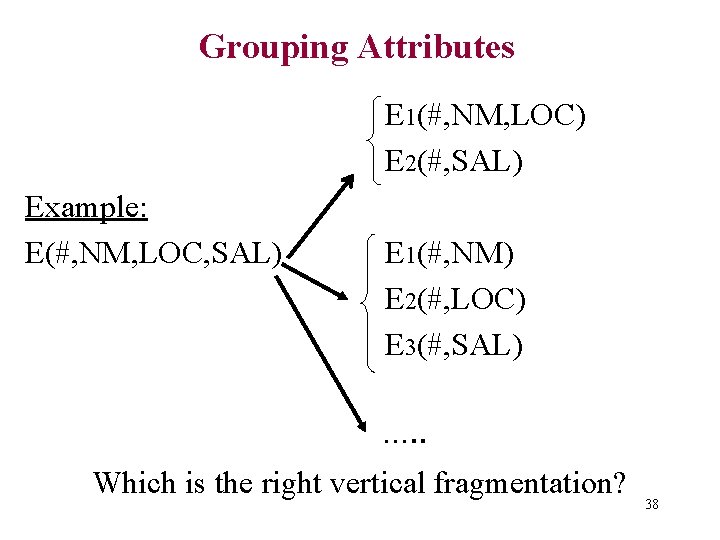
Grouping Attributes E 1(#, NM, LOC) E 2(#, SAL) Example: E(#, NM, LOC, SAL) E 1(#, NM) E 2(#, LOC) E 3(#, SAL) …. . Which is the right vertical fragmentation? 38

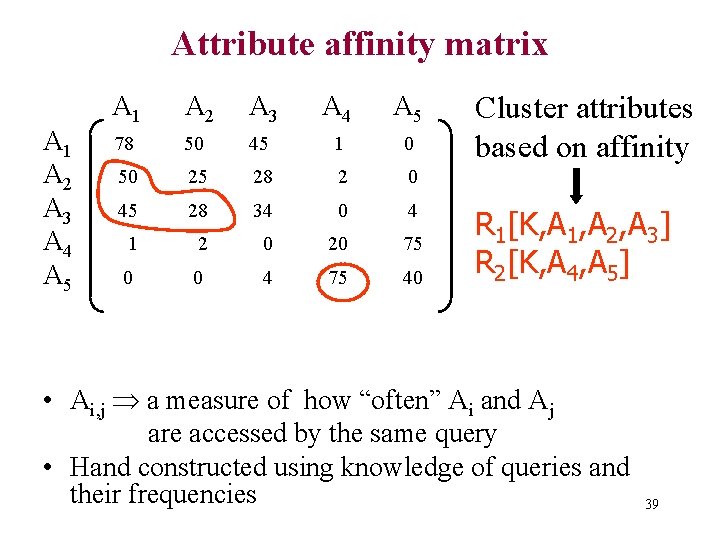
Attribute affinity matrix A 1 A 2 A 3 A 4 A 5 78 50 45 1 0 50 25 28 2 0 45 28 34 0 4 1 2 0 20 75 0 0 4 75 40 Cluster attributes based on affinity R 1[K, A 1, A 2, A 3] R 2[K, A 4, A 5] • Ai, j a measure of how “often” Ai and Aj are accessed by the same query • Hand constructed using knowledge of queries and their frequencies 39

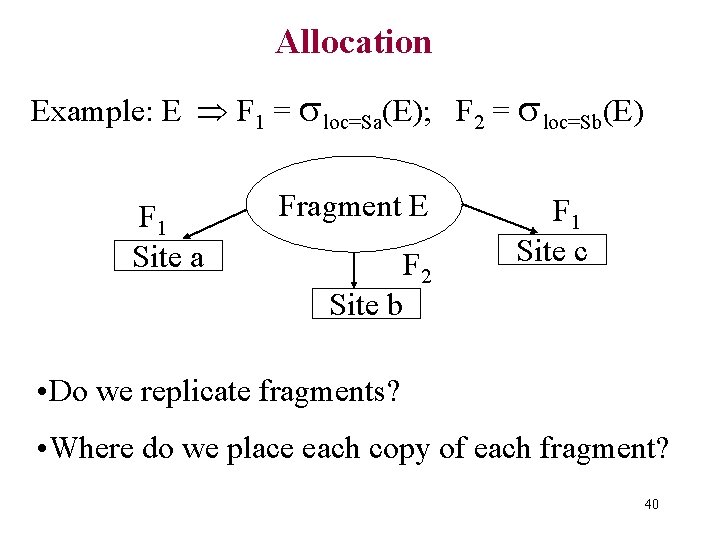
Allocation Example: E F 1 = loc=Sa(E); F 2 = loc=Sb(E) F 1 Site a Fragment E Site b F 2 F 1 Site c • Do we replicate fragments? • Where do we place each copy of each fragment? 40

Issues • Origin of queries • Communication cost and size of answers, relations, etc. • Storage capacity, storage cost at sites, and size of fragments • Processing power at the sites • Query processing strategy – How are joins done? Where answers collected? • Fragment replication – Update cost, concurrency control overhead 41

Optimization problem • What is the best placement of fragments and/or best number of copies to: – minimize query response time – maximize throughput – minimize “some cost” Very hard problem –. . . • Subject to constraints – Available storage – Available bandwidth, processing power, … – Keep 90% of response time below X –. . . 42