Distributed Computing 2 Leader Election ring network Shmuel

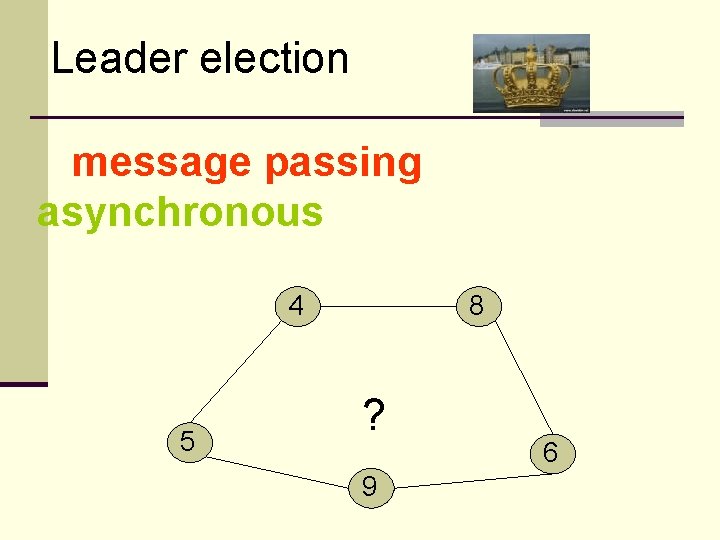
Leader election message passing asynchronous 4 5 8 ? 9 6

(Leader election) Ømotivation Ø who starts? ØLeader election, maximum finding, spanning tree

(Leader election) Ø Unidirectional ring Ø Bidirectional rings Ø Complete networks Ø General networks

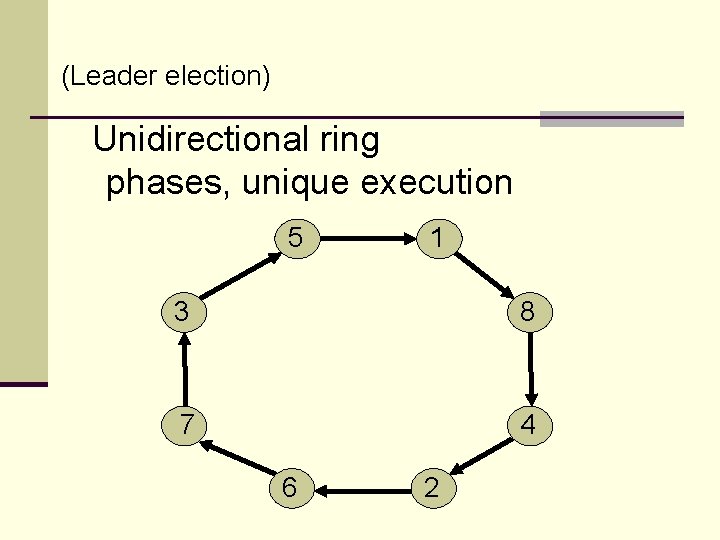
(Leader election) Unidirectional ring phases, unique execution 5 1 3 8 7 4 6 2

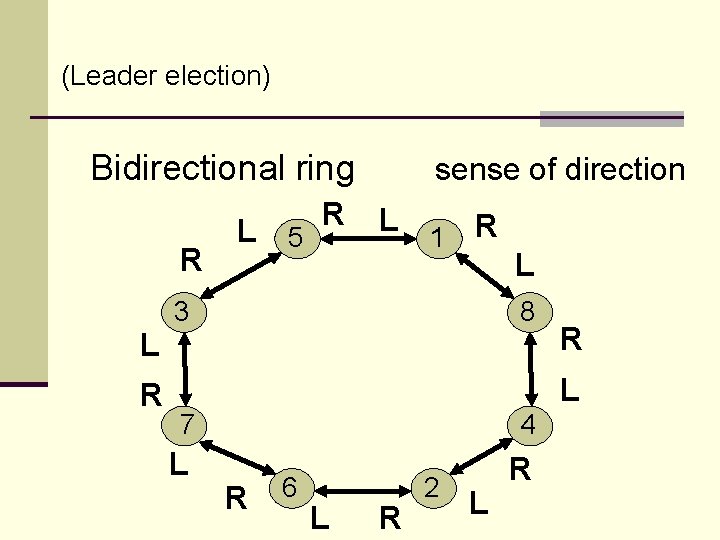
(Leader election) Bidirectional ring R L 5 R sense of direction L 1 R L 3 8 L R R L 7 4 L R R 6 L R 2 L

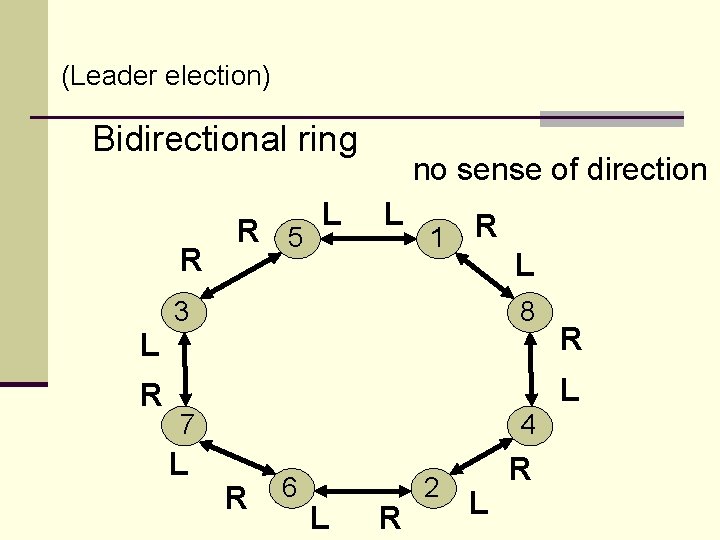
(Leader election) Bidirectional ring R R 5 L no sense of direction L 1 R L 3 8 L R R L 7 4 L R R 6 L R 2 L

Sense of Direction: For each process p in a bidirectional ring, its left and right neighbors are termed left(p) and right(p) respectively. If right(left(p)) = p for every p, then there is a sense of direction (otherwise – no sense of direction)

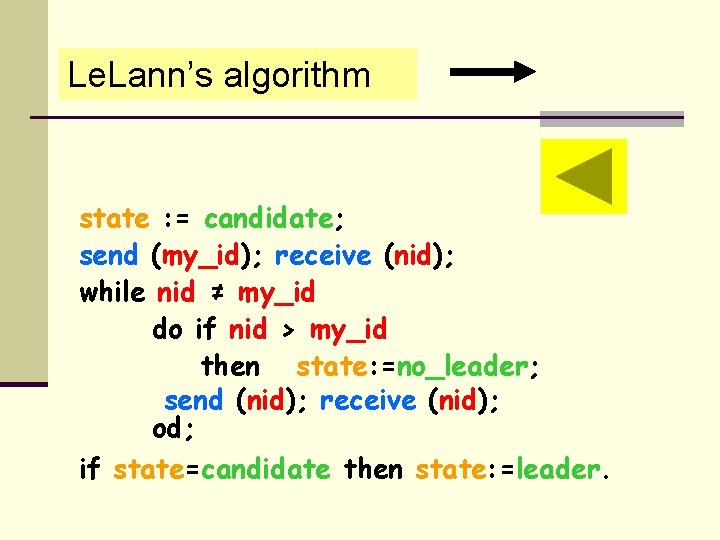
Le. Lann’s algorithm state : = candidate; send (my_id); receive (nid); while nid ≠ my_id do if nid > my_id then state: =no_leader; send (nid); receive (nid); od; if state=candidate then state: =leader.

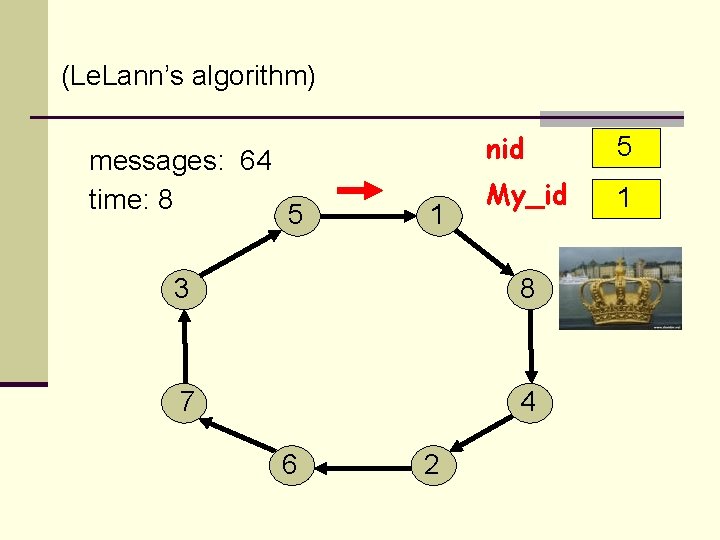
(Le. Lann’s algorithm) messages: 64 time: 8 5 1 nid 5 My_id 1 3 8 7 4 6 2

(Le. Lann’s algorithm) Theorem: Le. Lann’s algorithm terminates, and exactly one processor is in state= leader. Message complexity: O(n 2) (worst and average) Time complexity: O(n)

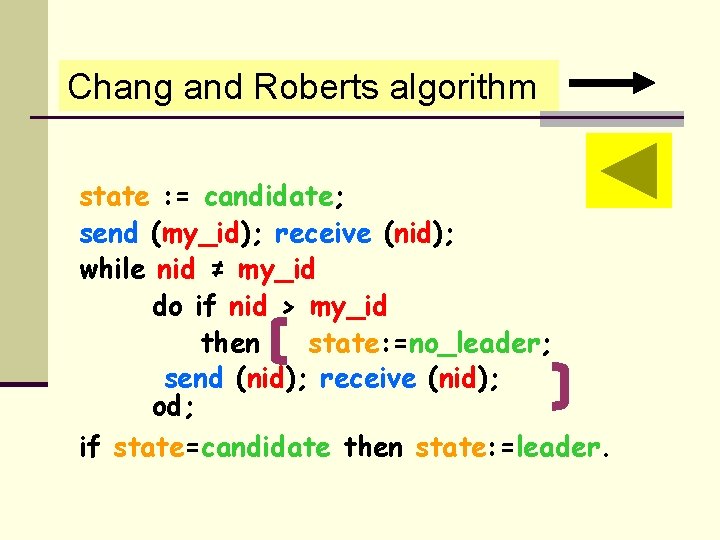
Chang and Roberts algorithm state : = candidate; send (my_id); receive (nid); while nid ≠ my_id do if nid > my_id then state: =no_leader; send (nid); receive (nid); od; if state=candidate then state: =leader.

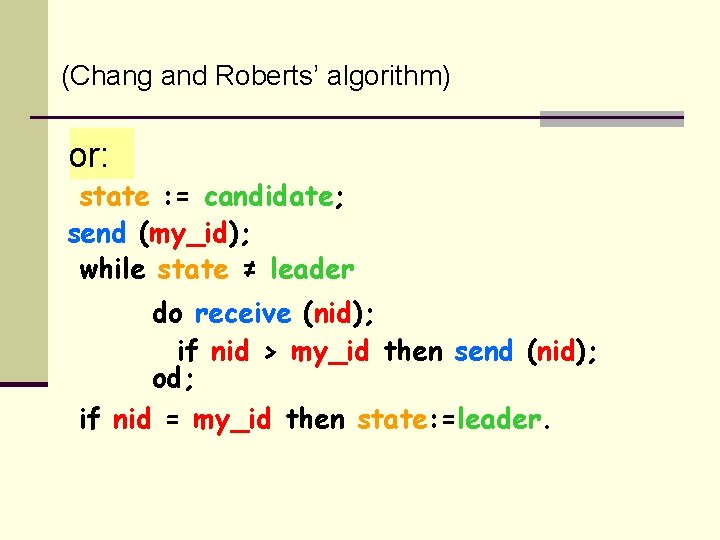
(Chang and Roberts’ algorithm) or: state : = candidate; send (my_id); while state ≠ leader do receive (nid); if nid > my_id then send (nid); od; if nid = my_id then state: =leader.

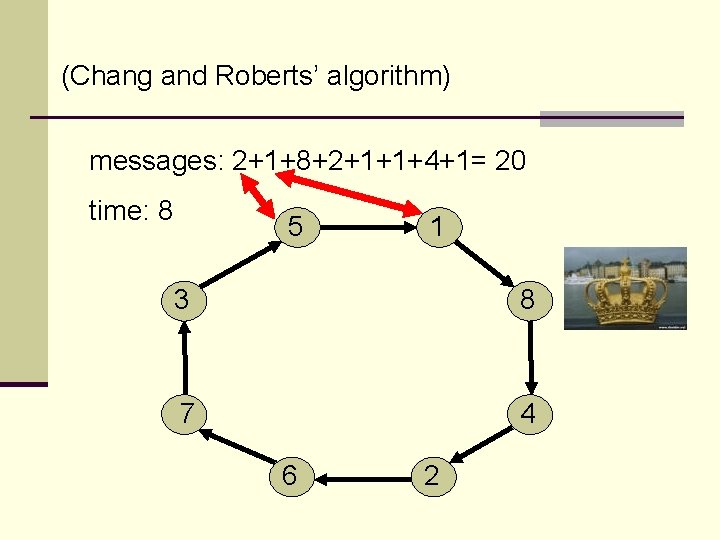
(Chang and Roberts’ algorithm) messages: 2+1+8+2+1+1+4+1= 20 time: 8 5 1 3 8 7 4 6 2

(Chang and Roberts’ algorithm) Theorem: Chang and Roberts’s algorithm terminates, and exactly one processor is in state= leader. Message complexity: O(n 2) (worst) Time complexity: O(n)

(Chang and Roberts’ algorithm) Theorem: The average message complexity of Chang and Roberts’s algorithm is O(n log n). assume all rings equally probably (for the proof – assume ids are 1, 2, …, n)

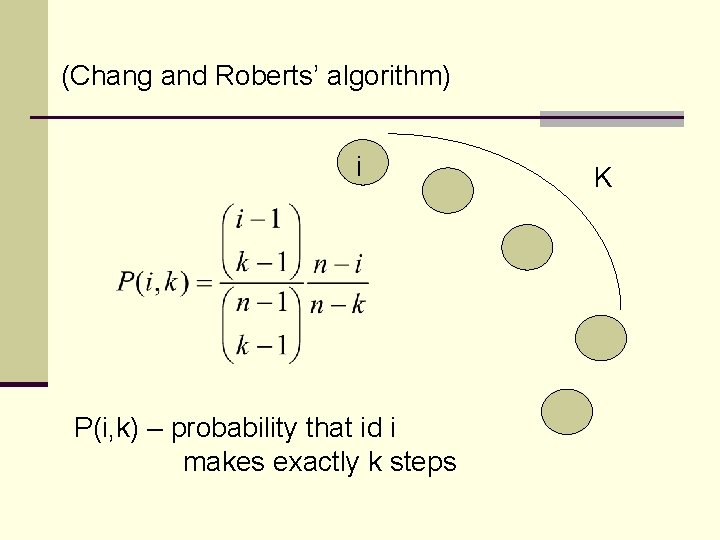
(Chang and Roberts’ algorithm) i P(i, k) – probability that id i makes exactly k steps K

(Chang and Roberts’ algorithm)

(Chang and Roberts’ algorithm) or: Consider all rings • Each id makes 1 step – times • Identity of Pi: makes 2 nd step iff it is largest among Pi, Pi+1, which happens times • Identity of Pi: makes 3 rd step iff it is largest among Pi, Pi+1, Pi+2, which happens times, • etc …

Bidirectional rings messages: ? time: ? 5 1 3 8 7 4 6 2

Hirschberg and Sinclair’s algorithm Phases 1, 2, … processors start phase k no. of phases messages time = O(n)

Franklin’s algorithm messages: ? time: ? 5 1 3 8 7 4 6 2

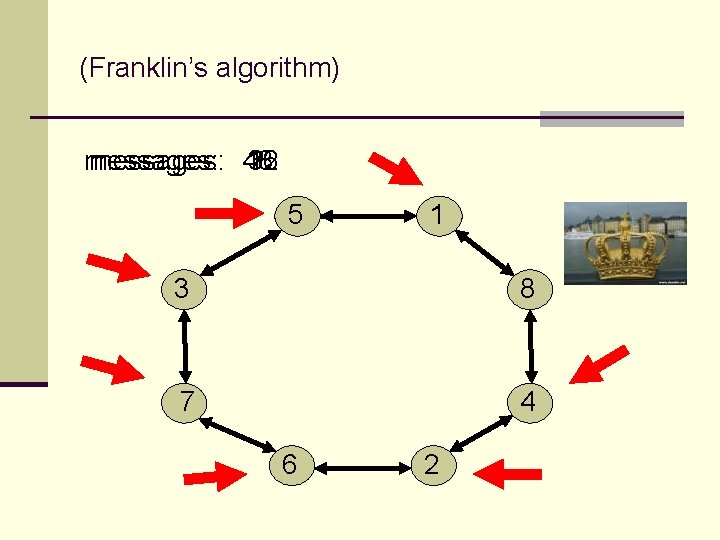
(Franklin’s algorithm) messages: 48 ? 16 32 5 1 3 8 7 4 6 2

(Franklin’s algorithm) no. of phases messages time = O(n) Exercise: what is the expected number of active processors after the first phase?

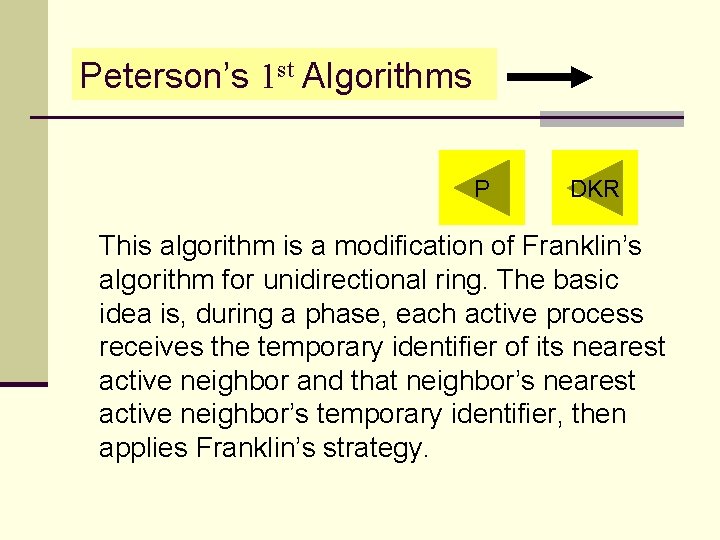
Peterson’s 1 st Algorithms P DKR This algorithm is a modification of Franklin’s algorithm for unidirectional ring. The basic idea is, during a phase, each active process receives the temporary identifier of its nearest active neighbor and that neighbor’s nearest active neighbor’s temporary identifier, then applies Franklin’s strategy.

(Peterson’s 1 st Algorithms) Each node maintains four variables: state {candidate, relay, leader} tid – temporary identity ntid – first id received nntid – second id received

state: = candidate; tid: =id; while state relay do begin [start phase] send(tid); receive(ntid); if ntid = id then state : =leader; if tid > ntid then send(tid); else send(ntid); receive(nntid); if nntid = id then state : = leader; if ntid max(tid, nntid) then tid: =ntid else state : = relay; end; (now state = relay)

(now state = relay) while state leader do begin receive(tid); if tid=id then state : =leader; send(tid); end

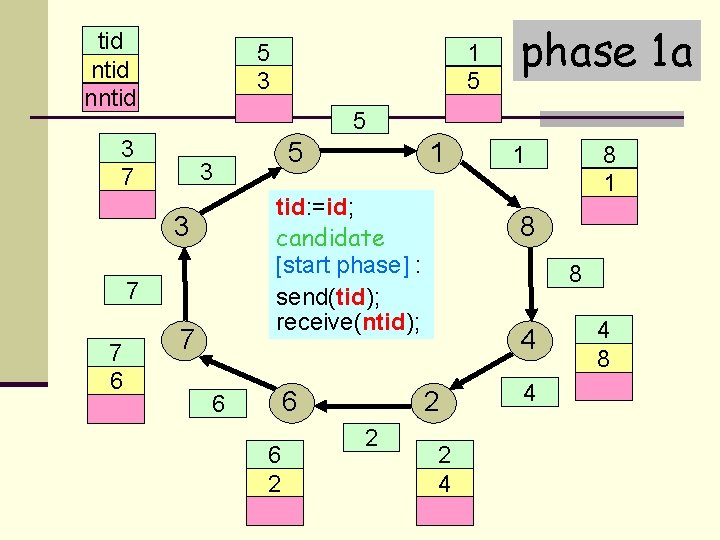
tid nntid 5 3 phase 1 a 5 3 7 5 3 1 tid: =id; candidate [start phase] : send(tid); receive(ntid); 3 7 7 6 1 5 7 6 6 6 2 8 8 4 2 2 8 1 1 2 4 4 4 8

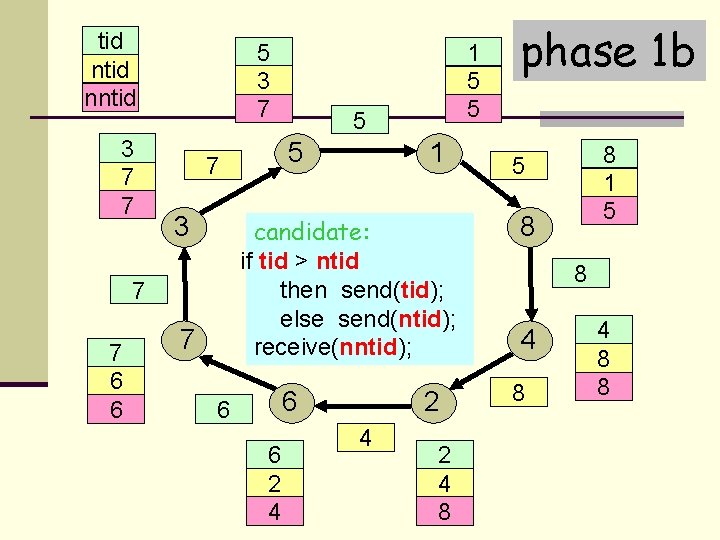
tid nntid 3 7 7 5 3 7 3 1 candidate: if tid > ntid then send(tid); else send(ntid); receive(nntid); 7 7 6 6 5 5 7 1 5 5 7 6 6 6 2 4 2 4 8 phase 1 b 8 1 5 5 8 8 4 8 8

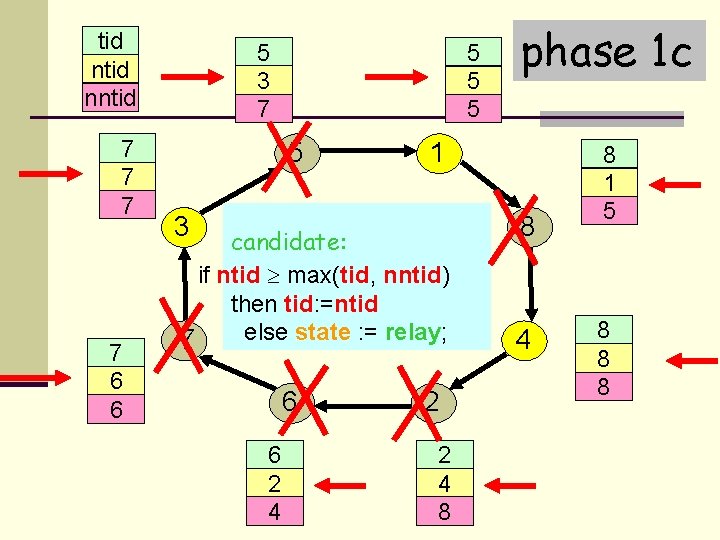
tid nntid 7 3 7 7 7 6 6 5 3 7 5 1 5 5 5 11 3 candidate: if ntid max(tid, nntid) then tid: =ntid else state : = relay; 7 6 6 2 4 phase 1 c 2 2 4 8 8 4 8 1 5 4 8 8 8

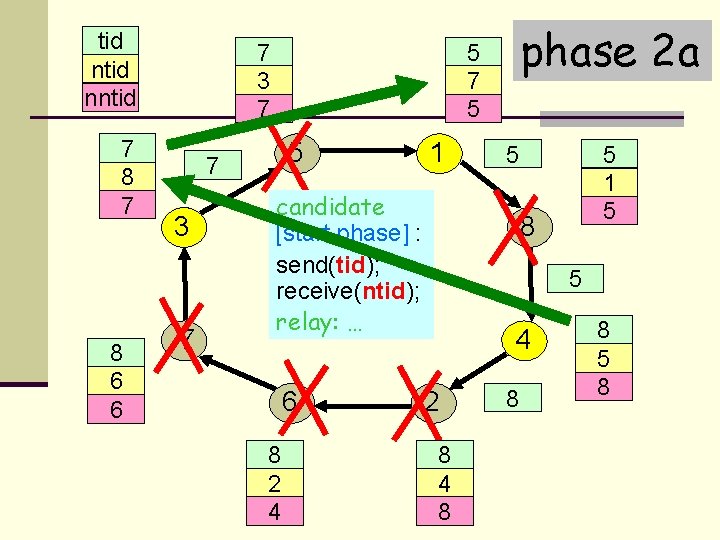
tid nntid 7 3 7 8 7 7 8 6 6 5 7 3 7 phase 2 a 5 1 7 5 5 11 candidate [start phase] : send(tid); receive(ntid); relay: … 6 6 8 2 4 5 5 8 1 5 8 5 4 2 2 8 4 8 8 5 8

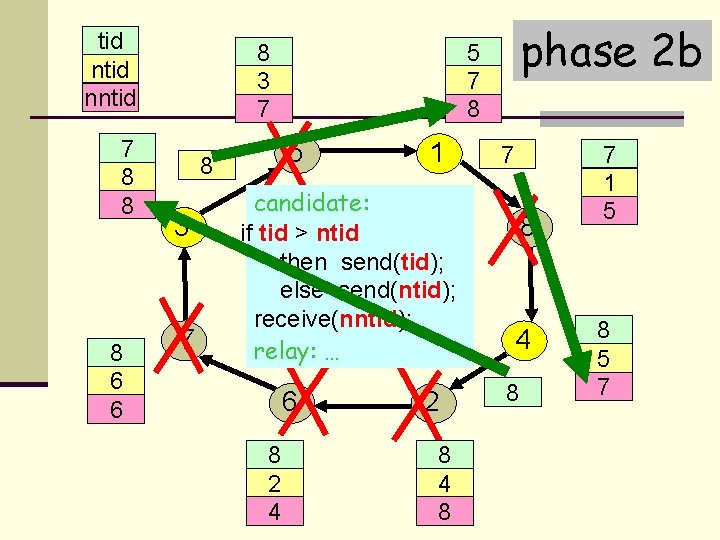
tid nntid 7 3 7 8 7 8 6 6 8 5 7 3 7 5 8 3 7 11 candidate: if tid > ntid then send(tid); else send(ntid); receive(nntid); relay: … 6 6 8 2 4 phase 2 b 5 1 7 5 5 8 2 2 8 4 8 7 8 5 1 5 4 8 8 5 8 7

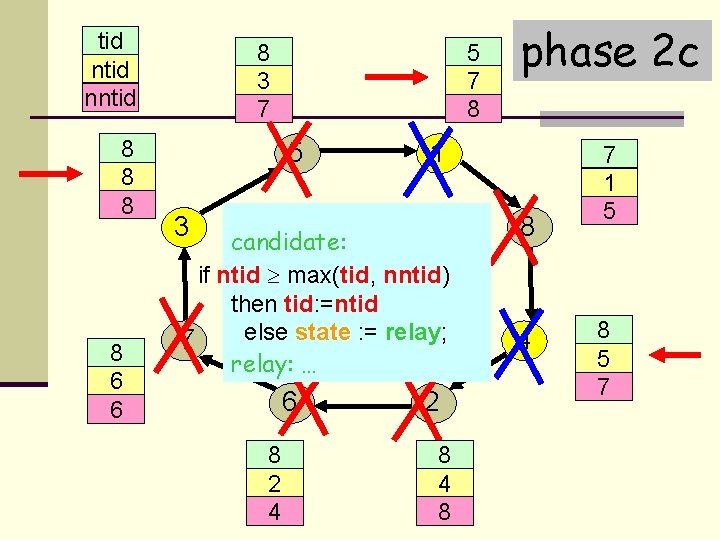
tid nntid 8 3 7 7 8 7 8 6 6 8 5 7 3 7 5 1 7 5 5 8 5 11 3 candidate: if ntid max(tid, nntid) then tid: =ntid else state : = relay; 7 relay: … 6 6 8 2 4 phase 2 c 2 2 8 4 8 8 4 7 8 5 1 5 4 8 8 5 8 7

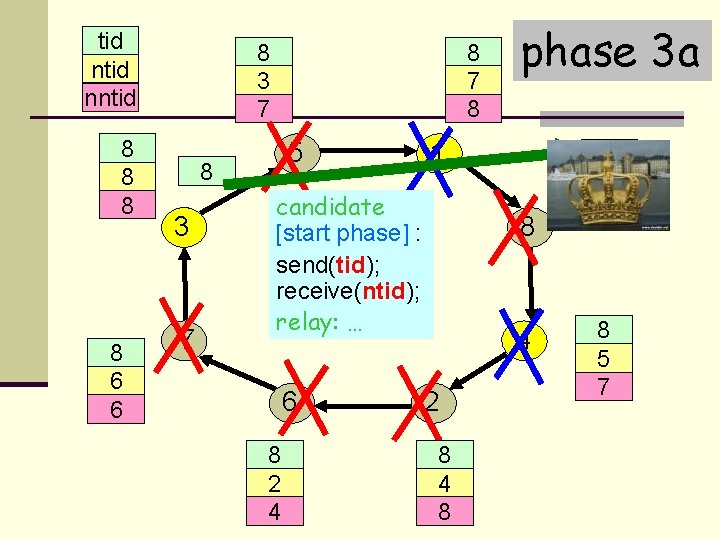
tid nntid 8 3 7 7 8 7 8 6 6 8 5 7 3 7 8 1 5 7 5 5 8 3 7 11 candidate [start phase] : send(tid); receive(ntid); relay: … 6 6 8 2 4 phase 3 a 8 4 2 2 8 4 8 8 5 7 1 5 4 8 8 5 8 7

Exercises: 1. why send max{tid, ntid}? 2. what happens if n=2? 3. what happens if n=1?

Pmax – processor holding max_id Phase 1, 2, … tp - number of non-relay processors starting phase p. Lemma: During the execution of the algorithm, a candidate processor that becomes relay will never be in a candidate state. Lemma: For every p, if tp ≥ 3 then tp+1 ≤ tp / 2.

Lemma: if tp ≥ 3 then at the start of phase p: n Each identity resides as the tid of at most one candidate processor. n If the id of Pi resides in Pk, then all processors Pi, Pi+1, …, Pk-1 are relays. n max_id resides as a tid of some processor. n Lemma: if tp = 2 or tp = 1 then the algorithm terminates, with the processor holding max_id as a leader.

Theorem: Peterson’s 1 st algorithm always determines a unique processor – the one holding the largest identity - as a leader. Message complexity ≤ 2 n log n Time complexity ≤ 2 n-1 Exercise: show examples for worst cases and for best cases in terms of time and in terms of messages.

n Peterson’s 2 nd Algorithm improvement of Peterson’s 1 st algorithm Instead of comparing its id with both neighbors in the same time, a process first compares itself with its left neighbor, then its right neighbor.

(Peterson’s 2 nd Algorithms) Each node maintains four variables: state {candidate, relay, leader} tid – temporary identity ntid – id received

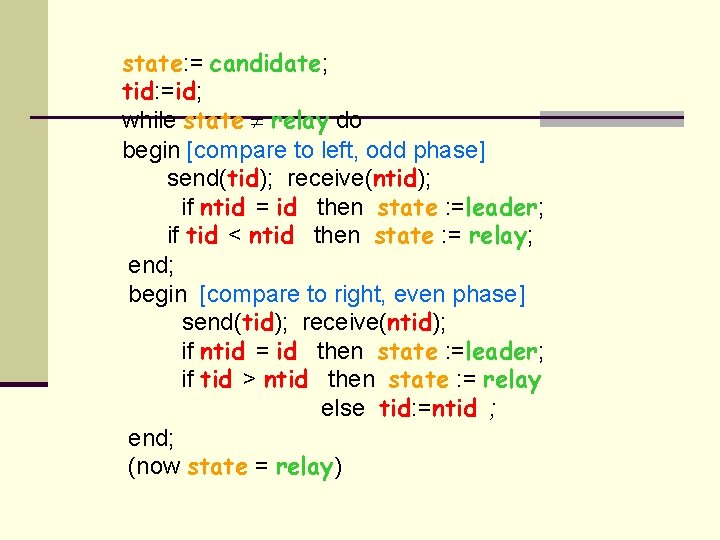
state: = candidate; tid: =id; while state relay do begin [compare to left, odd phase] send(tid); receive(ntid); if ntid = id then state : =leader; if tid < ntid then state : = relay; end; begin [compare to right, even phase] send(tid); receive(ntid); if ntid = id then state : =leader; if tid > ntid then state : = relay else tid: =ntid ; end; (now state = relay)

(now state = relay) while state leader do begin receive(tid); if tid=id then state : =leader; send(tid); end

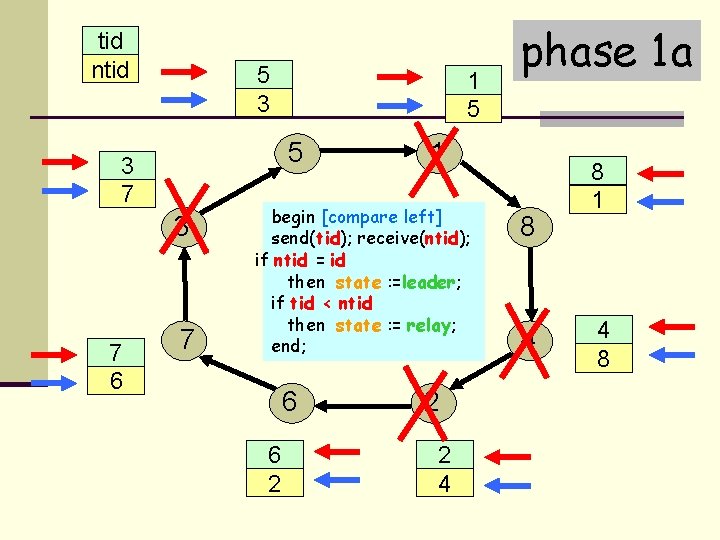
tid ntid 5 3 7 3 7 6 1 5 7 1 begin [compare left] send(tid); receive(ntid); if ntid = id then state : =leader; if tid < ntid then state : = relay; end; 6 6 2 phase 1 a 2 2 4 8 1 4 8

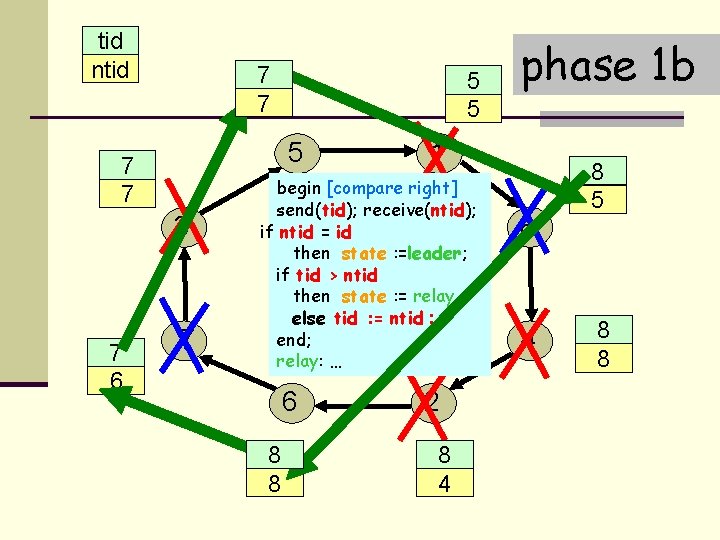
tid ntid 7 5 3 7 5 7 3 7 6 5 1 5 7 1 begin [compare right] send(tid); receive(ntid); if ntid = id then state : =leader; if tid > ntid then state : = relay else tid : = ntid ; end; relay: … 6 6 8 2 8 phase 1 b 2 2 8 4 8 1 5 4 8 8

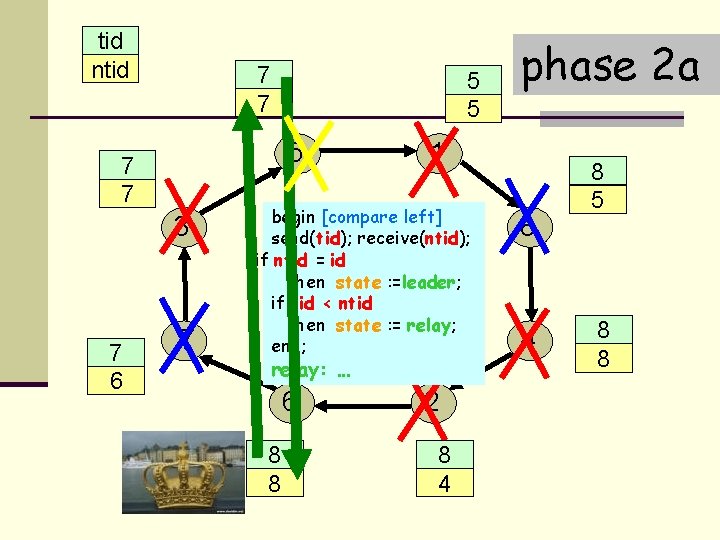
tid ntid 7 3 7 5 7 3 7 6 5 1 5 7 1 begin [compare left] send(tid); receive(ntid); if ntid = id then state : =leader; if tid < ntid then state : = relay; end; relay: … 6 8 2 8 phase 2 a 2 2 8 4 8 1 5 4 8 8

Theorem: Peterson’s 2 nd algorithm always determines a unique processor as a leader. Message complexity ≤ 1. 44… n log n Exercise: show an example where a processor whose id is not the largest is elected as a leader.

phases p, p-1, … 1 (last phase) tk – no. of processors that remain candidates after phase k = no. of processors that start ase k-1. tp+1 = n t 1 = 1 t 2 ≥ 2

Lemma: tk ≤ no. of processors that became relay during phase k+1 Proof: We show that for each processor that remained active after phase k there is a processor that became relay during phase k+1 (the previous phase)

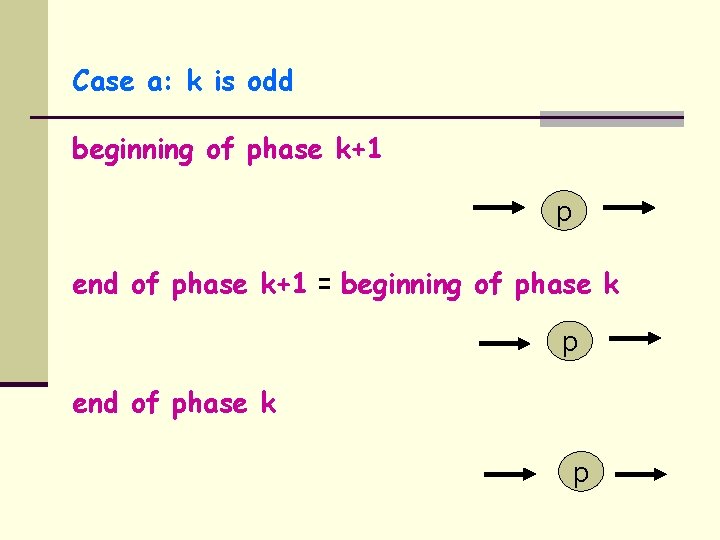
Case a: k is odd beginning of phase k+1 p end of phase k+1 = beginning of phase k p end of phase k p

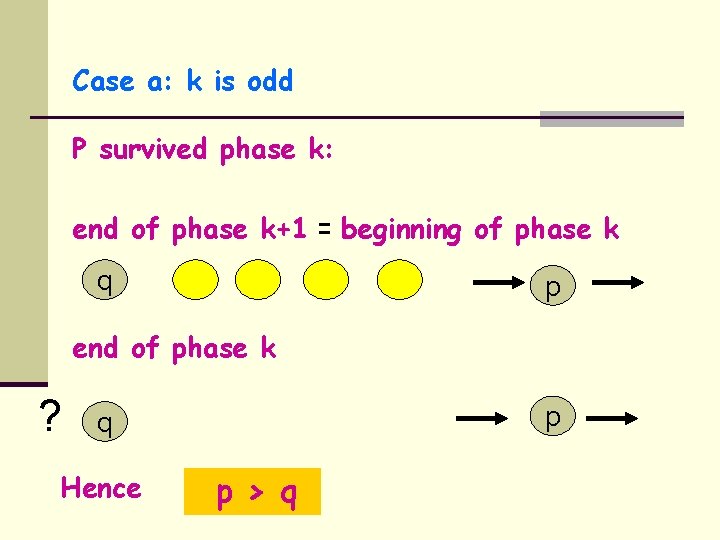
Case a: k is odd P survived phase k: end of phase k+1 = beginning of phase k q p end of phase k ? p q Hence p > q

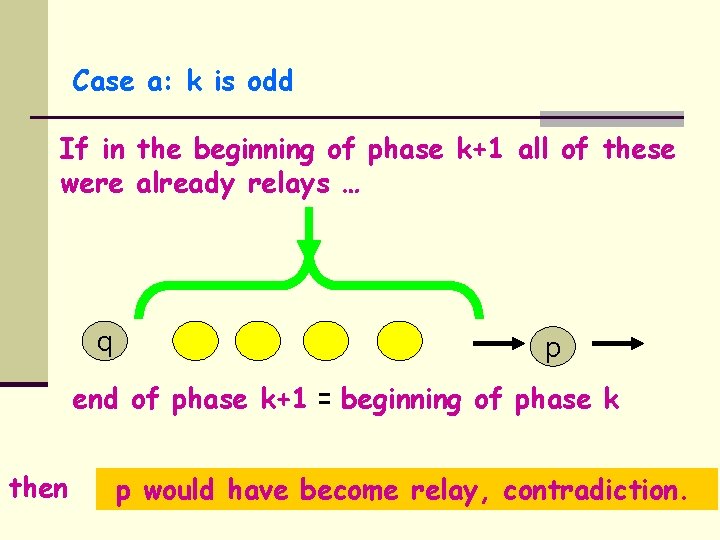
Case a: k is odd If in the beginning of phase k+1 all of these were already relays … q p end of phase k+1 = beginning of phase k then p would have become relay, contradiction.

Lemma: tk ≤ no. of processors that became relay during phase k+1 Corollary: tk ≤ tk+2 - tk+1 tk + tk+1 ≤ tk+2 tk ≥ Fibonaccik+1 =

n = tp+1 ≥ Fibonaccip+2 = no. of phases = p ≤ 1. 44… log n message complexity ≤ np ≤ 1. 44… n log n

References E. Chang and R. Roberts, An improved algorithm for decentralized extrema-finding in circular configurations of processes, Communications of the ACM}, 22, 5, 1979, pp. 281 -283.

References D. Dolev, M. Klawe and M. Rodeh, An O(n log n) unidirectional distributed algorithm for extrema finding in a circle, Journal of Algorithms, 3, 1982, pp. 245 -260.

References W. R. Franklin, On an improved algorithm for decentralized extrema finding in circular configurations of processors, Communication of the ACM, 25, 1982, pp. 336 -337.

References D. S. Hirschberg and J. B. Sinclair, Decentralized extrema-finding in circular configuration of processors, Communications of the ACM, 23, 1980, pp. 627 -628.

References G. Le. Lann, Distributed systems - towards a formal approach, Information Processing Letters, 1977, pp. 155 -160.

References G. L. Peterson An O(nlogn) unidirectional algorithm for the circular extrema problem. ACM Trans. Program. Lang. Syst. 4, 4 (Oct. 1982), 758 -762.

References N. Santoro, Sense of direction, topological awareness and communication complexity, SIGACT News, 16, 2, Summer 1984, pp. 50 -56.