Distributed and MultiTimeConstant Electrothermal Modeling and Its Impact

Distributed and Multi-Time-Constant Electro-thermal Modeling and Its Impact on RF Predistortion Wenhua Dai, The Ohio State University Patrick Roblin, The Ohio State University Michel Frei, Agere Systems 1

Outline • Introduction • Electrical modeling • Image method in thermal modeling • Distributed thermal model • Multi-time-constant thermal model • Thermal memory effects in RF predistorter • Conclusion 2

Introduction • High power devices self-heat during operation, which affects its electrical performances. • Most of the power device models use simple low pass RC circuit to model the self-heating • The non-uniformly distributed temperature across the power device requires a model to capture the temperature distribution • Dynamic self-heating due to the low frequency modulation envelop causes thermal memory effects. • Memory effects are categorized into thermal and electrical memory effects. They are usually bonded together and it is difficult to quantify each of them separately. • Temperature rise in a multilayer material involves fast and slow time constants. Simple RC model can’t capture them. 3

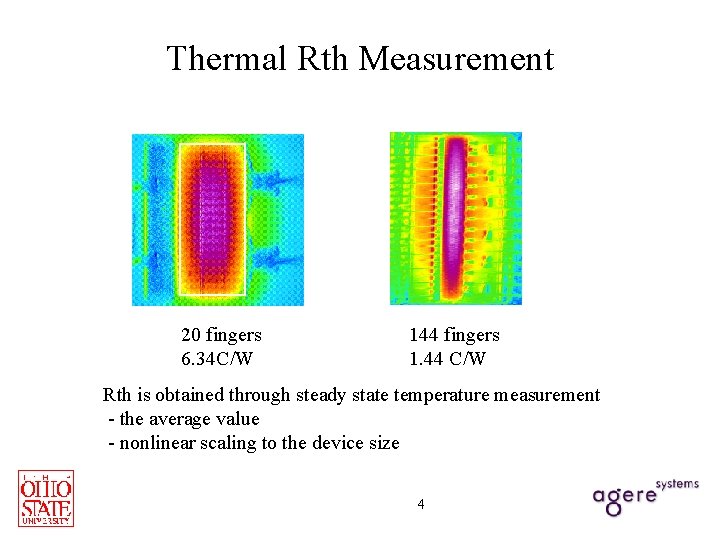
Thermal Rth Measurement 20 fingers 6. 34 C/W 144 fingers 1. 44 C/W Rth is obtained through steady state temperature measurement - the average value - nonlinear scaling to the device size 4

Thermal Time Constant Measurement Thermal time constant is obtained through pulse IV measurement, Drain current decrease/increase due to the heating ID (A) - Measured rise time maybe affected by Cgs, Ls, and power supplier - Two competing thermal effects (Vth, mobility) may cancel each other, resulting less thermal effects 0 Time (s) 6 x 10 -6 5

Large Signal Electro-Thermal Model D G • Nonlinear large signal electrical model • IV characterization from both iso-thermal and pulse measurement Electrical part Thermal part S Tsub • S-parameter characterization from isothermal measurement • Parasitics from cold FET measurement • Simple RC circuit to model the temperature response Tdev 6

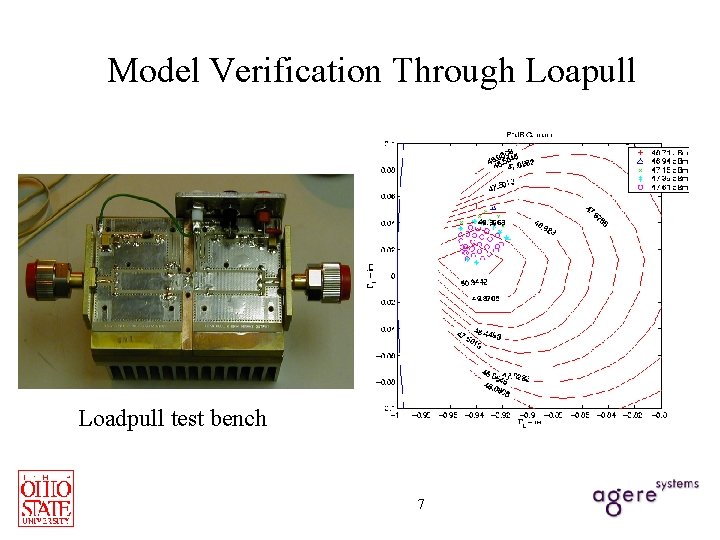
Model Verification Through Loapull Loadpull test bench 7

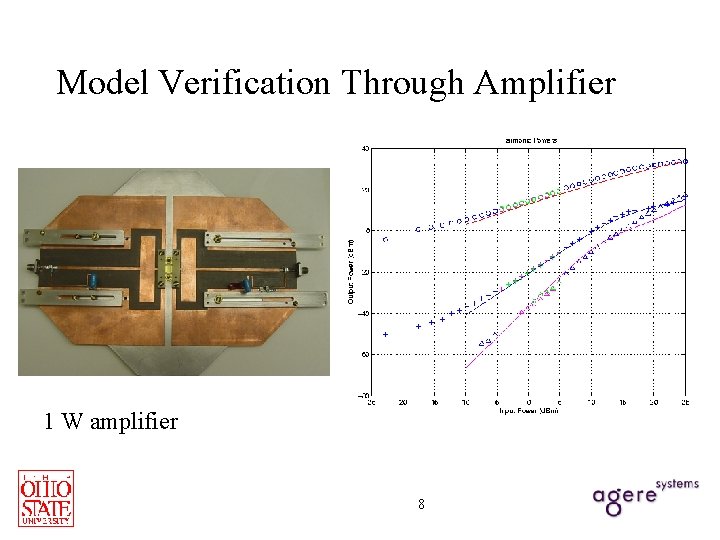
Model Verification Through Amplifier 1 W amplifier 8

Part I: Lateral Thermal Model • 3 D steady state temperature calculation • Experimental Results • ADS implementation • Results 9

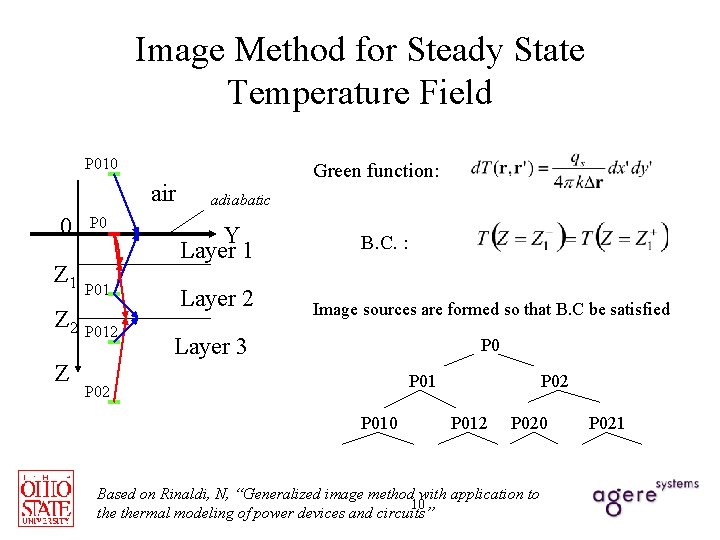
Image Method for Steady State Temperature Field P 010 air Green function: adiabatic 0 P 0 Z 1 Y Layer 1 P 01 Layer 2 Z P 012 B. C. : Image sources are formed so that B. C be satisfied Layer 3 P 01 P 02 P 010 P 02 P 012 P 020 Based on Rinaldi, N, “Generalized image method with application to 10 thermal modeling of power devices and circuits” P 021

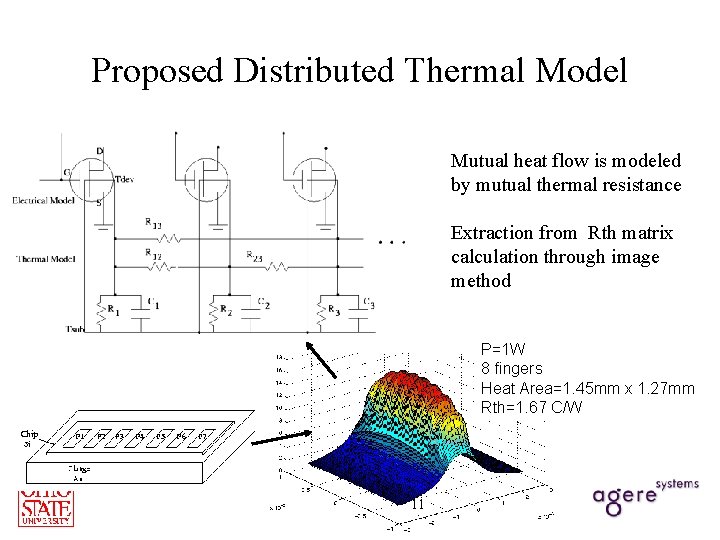
Proposed Distributed Thermal Model Mutual heat flow is modeled by mutual thermal resistance Extraction from Rth matrix calculation through image method P=1 W 8 fingers Heat Area=1. 45 mm x 1. 27 mm Rth=1. 67 C/W 11

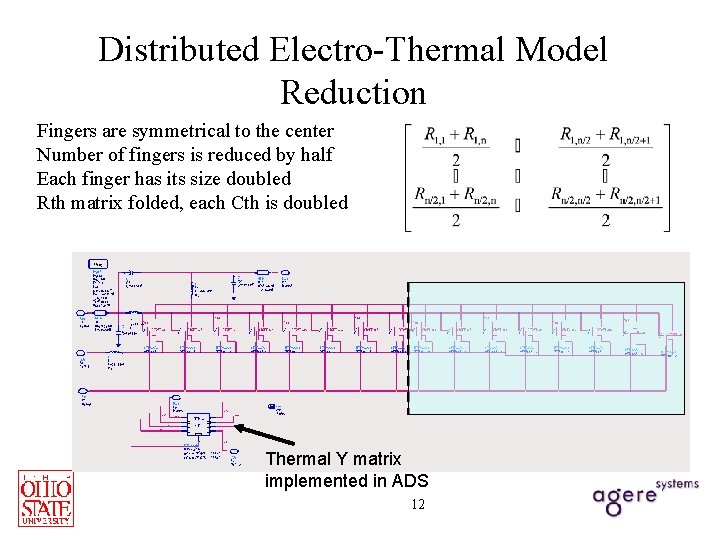
Distributed Electro-Thermal Model Reduction Fingers are symmetrical to the center Number of fingers is reduced by half Each finger has its size doubled Rth matrix folded, each Cth is doubled Thermal Y matrix implemented in ADS 12

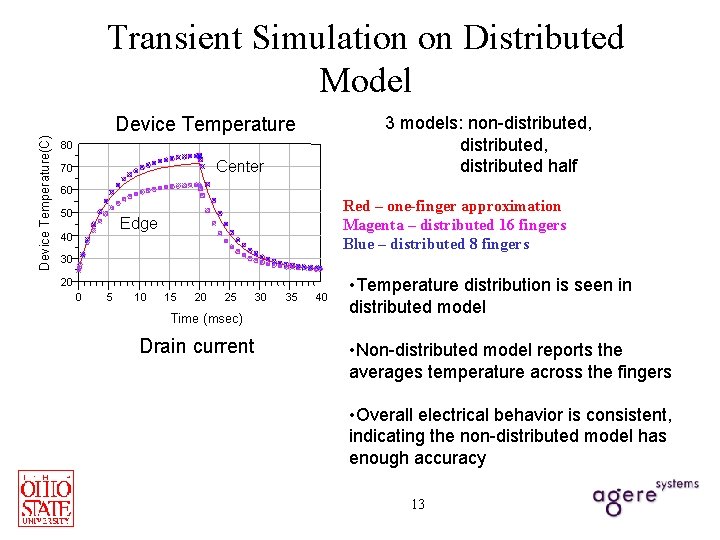
Device Temperature(C) Transient Simulation on Distributed Model 3 models: non-distributed, distributed half Device Temperature 80 Center 70 60 50 Red – one-finger approximation Magenta – distributed 16 fingers Blue – distributed 8 fingers Edge 40 30 20 0 5 10 15 20 25 Time (msec) Drain current 30 35 40 • Temperature distribution is seen in distributed model • Non-distributed model reports the averages temperature across the fingers • Overall electrical behavior is consistent, indicating the non-distributed model has enough accuracy 13

Part II: Transient Thermal Modeling and Memory effects • Approximate transient response with image method • Multistage RC model for ADS implementation • Impact of transient thermal model on a RF amplifier with a predistorter • Results for multisine excitation • Results for IS 95 CDMA excitation 14

Image Method for Approximated Transient Temperature Rise in Multilayer Structure Time dependent Green function of a rectangular heat source: X 2 X X 1 Y 2 Z 1 Y Layer 1 Layer 2 Boundary conditions: For all t Z Approximation 1: when D 1=D 2, boundary condition is independent of time, so that image method can be used Approximation 2: thermal conductivity of layer 2 is large enough 15

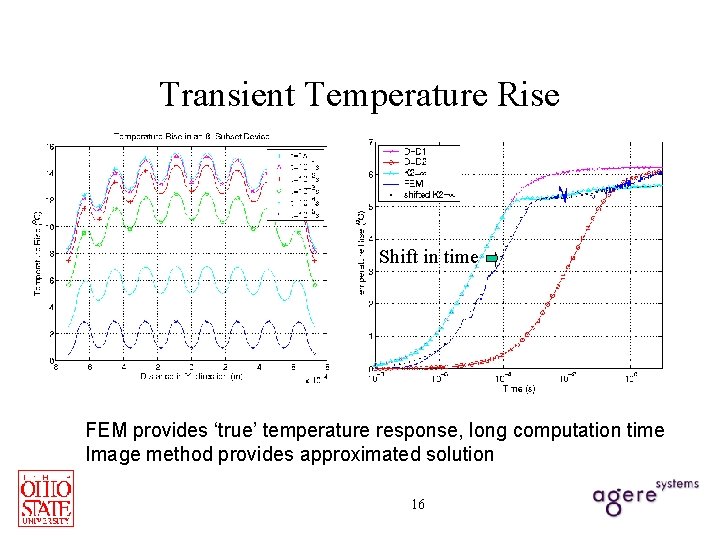
Transient Temperature Rise Shift in time FEM provides ‘true’ temperature response, long computation time Image method provides approximated solution 16

Proposed Multi-time-constant Thermal Model Slow and fast transient temperature rise can be modeled Rth includes junction, Si chip, flange, and copper block Extraction from transient temperature measurement/calculation 17

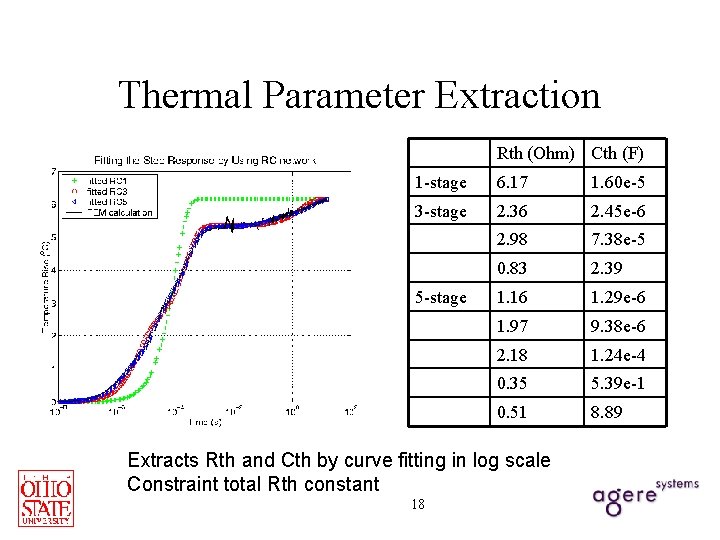
Thermal Parameter Extraction Rth (Ohm) Cth (F) 1 -stage 6. 17 1. 60 e-5 3 -stage 2. 36 2. 45 e-6 2. 98 7. 38 e-5 0. 83 2. 39 1. 16 1. 29 e-6 1. 97 9. 38 e-6 2. 18 1. 24 e-4 0. 35 5. 39 e-1 0. 51 8. 89 5 -stage Extracts Rth and Cth by curve fitting in log scale Constraint total Rth constant 18

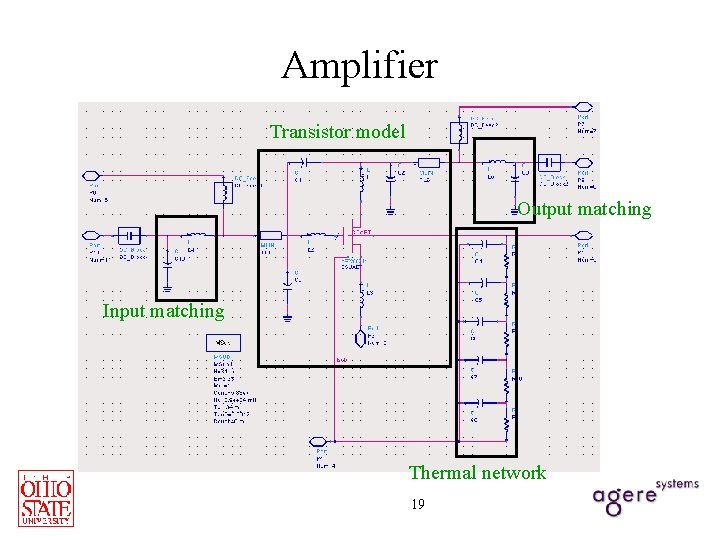
Amplifier Transistor model Output matching Input matching Thermal network 19

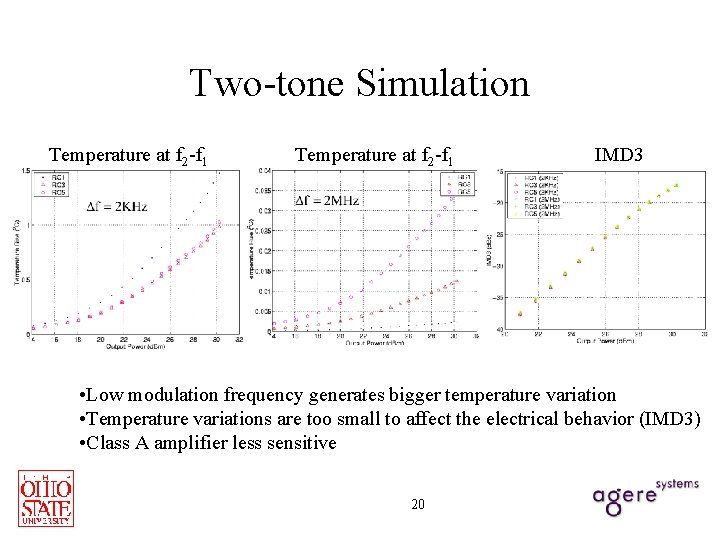
Two-tone Simulation Temperature at f 2 -f 1 IMD 3 • Low modulation frequency generates bigger temperature variation • Temperature variations are too small to affect the electrical behavior (IMD 3) • Class A amplifier less sensitive 20

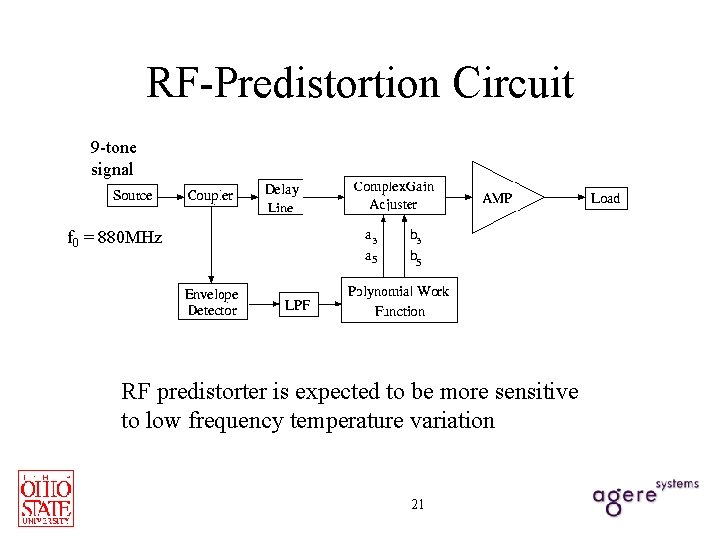
RF-Predistortion Circuit 9 -tone signal f 0 = 880 MHz RF predistorter is expected to be more sensitive to low frequency temperature variation 21

RF-Predistorter in ADS 9 -tone source signal Newman’s Phase (1965) f 0=880 MHz PAR=2. 6 22

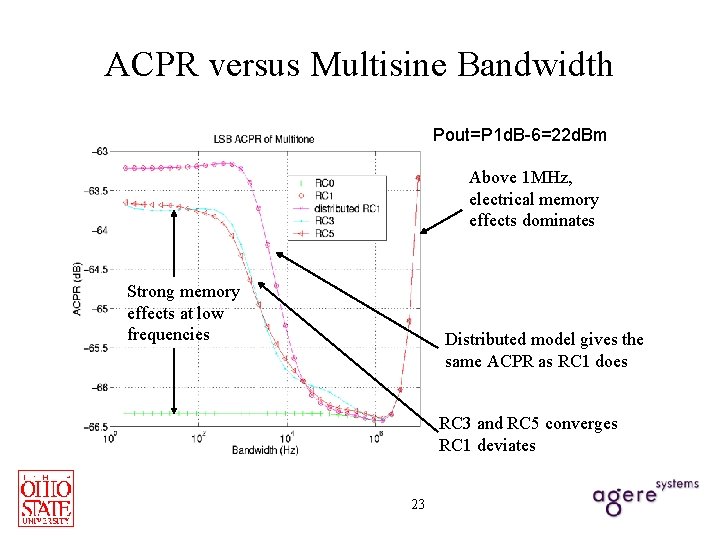
ACPR versus Multisine Bandwidth Pout=P 1 d. B-6=22 d. Bm Above 1 MHz, electrical memory effects dominates Strong memory effects at low frequencies Distributed model gives the same ACPR as RC 1 does RC 3 and RC 5 converges RC 1 deviates 23

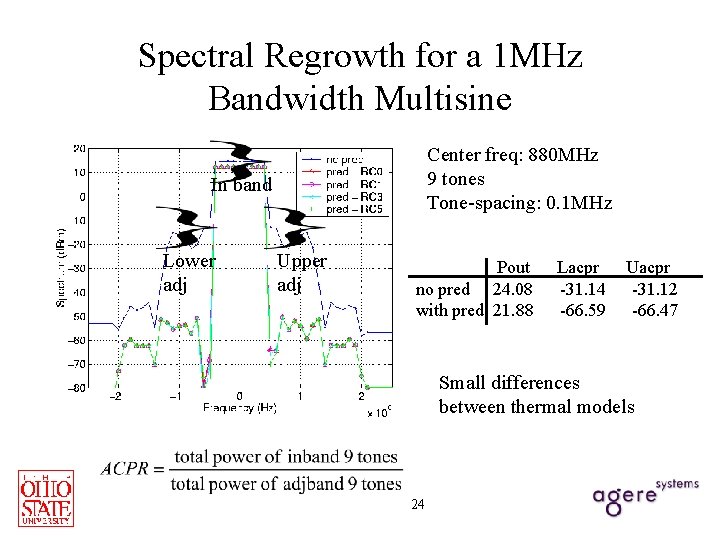
Spectral Regrowth for a 1 MHz Bandwidth Multisine Center freq: 880 MHz 9 tones Tone-spacing: 0. 1 MHz In band Lower adj Upper adj Pout no pred 24. 08 with pred 21. 88 Lacpr -31. 14 -66. 59 Uacpr -31. 12 -66. 47 Small differences between thermal models 24

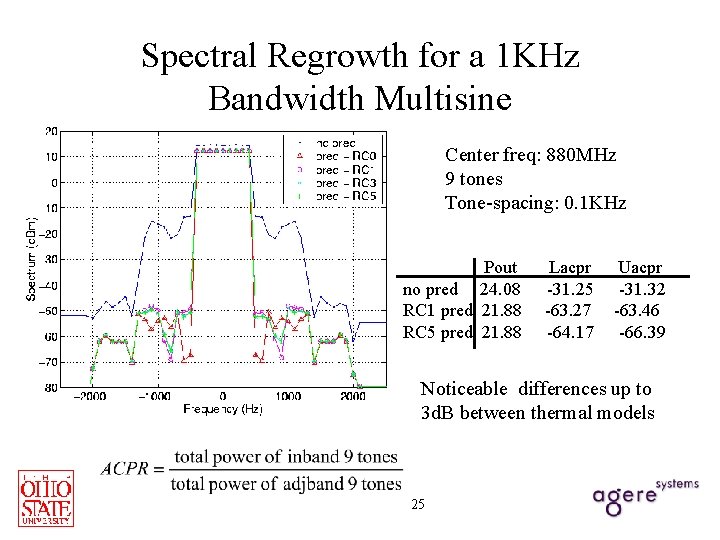
Spectral Regrowth for a 1 KHz Bandwidth Multisine Center freq: 880 MHz 9 tones Tone-spacing: 0. 1 KHz Pout no pred 24. 08 RC 1 pred 21. 88 RC 5 pred 21. 88 Lacpr -31. 25 -63. 27 -64. 17 Uacpr -31. 32 -63. 46 -66. 39 Noticeable differences up to 3 d. B between thermal models 25

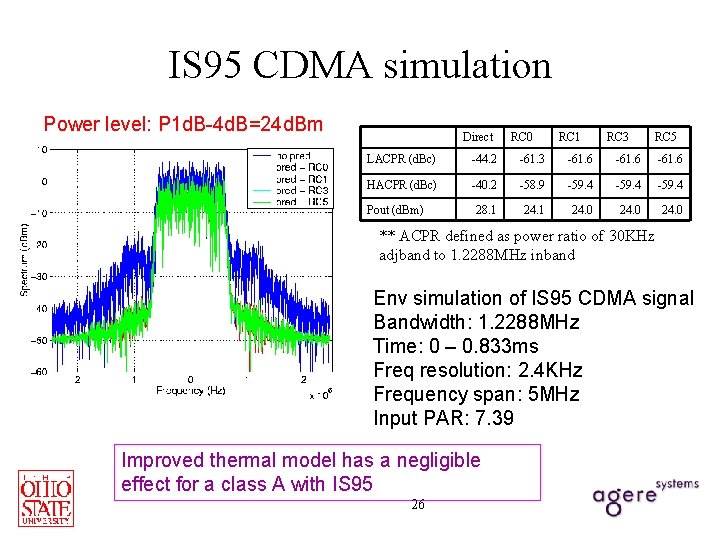
IS 95 CDMA simulation Power level: P 1 d. B-4 d. B=24 d. Bm Direct RC 0 RC 1 RC 3 RC 5 LACPR (d. Bc) -44. 2 -61. 3 -61. 6 HACPR (d. Bc) -40. 2 -58. 9 -59. 4 28. 1 24. 0 Pout (d. Bm) ** ACPR defined as power ratio of 30 KHz adjband to 1. 2288 MHz inband Env simulation of IS 95 CDMA signal Bandwidth: 1. 2288 MHz Time: 0 – 0. 833 ms Freq resolution: 2. 4 KHz Frequency span: 5 MHz Input PAR: 7. 39 Improved thermal model has a negligible effect for a class A with IS 95 26

Conditions for Strong Thermal Memory Effects • ACPR needs to be strongly sensitive to fluctuations of the temperature Note: ACPR is more sensitive to Delta T when using a predistorter (by a factor 10) Note: sensitivity is 0. 43 d. B/C (small) • Amplifier needs to exhibit a large fluctuation (variance) of the temperature Note: temperature fluctuation increases with input RF power and Rth 27

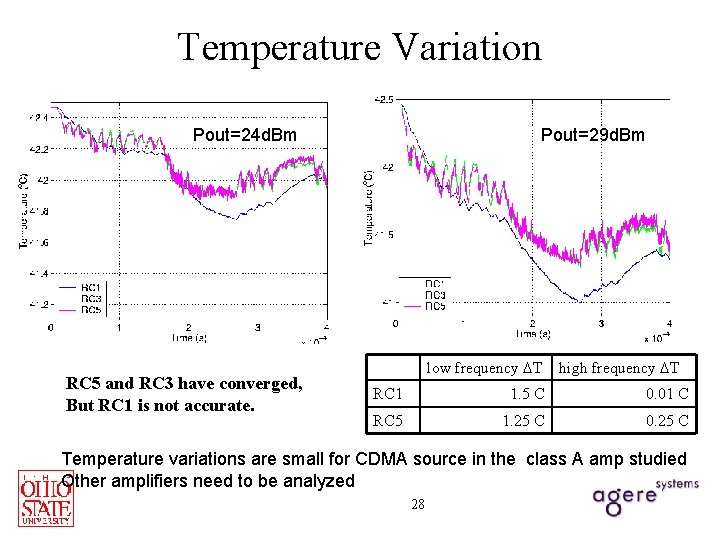
Temperature Variation Pout=24 d. Bm RC 5 and RC 3 have converged, But RC 1 is not accurate. Pout=29 d. Bm low frequency T high frequency T RC 1 1. 5 C 0. 01 C RC 5 1. 25 C 0. 25 C Temperature variations are small for CDMA source in the class A amp studied Other amplifiers need to be analyzed 28

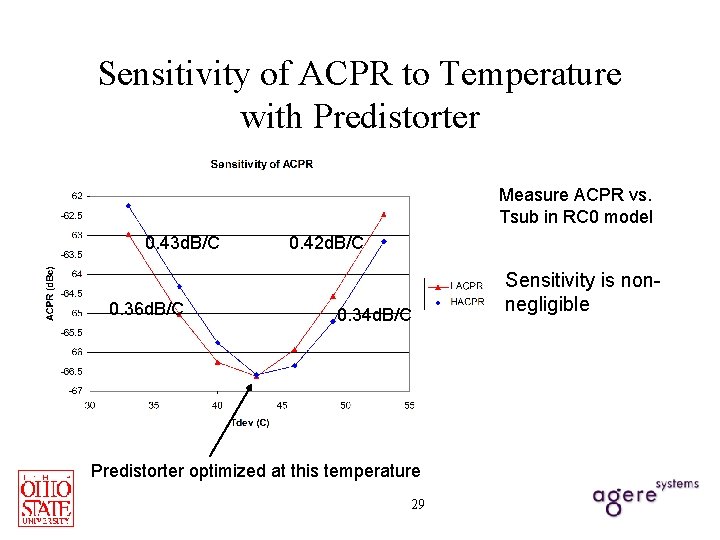
Sensitivity of ACPR to Temperature with Predistorter Measure ACPR vs. Tsub in RC 0 model 0. 43 d. B/C 0. 36 d. B/C 0. 42 d. B/C 0. 34 d. B/C Predistorter optimized at this temperature 29 Sensitivity is nonnegligible

Conclusion • An electro-thermal model for LDMOSFETs was extracted from RF and DC thermal measurement and implemented in ADS and used to design power amplifiers • Various thermal models were then compared to establish the impact of thermal memory effects on the predistortion linearization 30

Results for Part I: Lateral Distributed Thermal model • A recently reported image method for multilayer devices was implemented to study lateral distributed thermal effects in large multifinger devices. • Model was implemented in ADS using a distributed lateral thermal model using a single RC time constant for each finger. • Temperature distribution was reproduced. This is useful in applications where accurate temperature information is required. • The overall electrical behavior can be modeled with enough accuracy by a non-distributed model reproducing the average temperature. • Another application of distributed model is to predict the non-linear scaling of Rth with device area. 31

Results for Part II: Transient Thermal Modeling for Memory Effect in LDMOSFETs • An approximate image method was developed to predict the 3 D transient thermal response of a multi-layer LDMOSFET device. • Results obtained with the new model compares well with numerical results from transient FEM simulations. • 1, 3 and 5 stage RC thermal models are compared. Simulations show that RC 3 and RC 5 converged, and have better accuracy in reporting fast and low temperature fluctuations. • Thermal memory effects were found to be dominant over electrical memory effects with bandwith below 100 KHz • Electrical memory effects were found to dominate over thermal memory effects with bandwidth over 1 MHz • Thermal memory effects were demonstrated to have a negligible impact on the linearization of a class A amplifer for a IS 95 CDMA source. • The negligible impact of thermal memory effects on predistortion was verified to originate from the small temperature fluctuations (because of low Rth) and the low sensitivity of the LDMOSFET to these fluctuations. 32