Distributed Algorithms Distributed computing Key idea Buying 1000

Distributed Algorithms

Distributed computing • Key idea – Buying 1000 machines of speed x is significantly cheaper than buying one machine of speed 1000 x – No one person has to buy all 1000 machines: A lot of computational, communication and storage resources already in place and can be harvested for bigger things • Key challenge – Making the machines work together for effective speedup. Communication between machines is a key challenge. • Approaches – Find problems that can be distributed easily

Distributed problems • Problems that can use decentralized computing – Weather prediction • Weather in a location is most affected by weather nearby – Movie generation • Individual frames can be generated separately – Google search engine • 10, 000 s PC’s. all of them cheap, many of them identical • Can answer over 100, 000 queries per day in ½ sec or less each – Looking for the origin of the universe • Can be localized like weather prediction – File swapping and access (distributed storage) – Looking for extra terrestrial intelligence – Content caching and distribution

Distributed computers • Scales of distributed computing – Cluster-in-a-room hundreds of machines • All dedicated to the task – PCs on a campus thousands of machines • Using spare cycles – SETI cluster • Screen saver situation millions of machines

Cluster in a Room • Machines are dedicated to the network • All machines run similar software • Problem is divided into pieces – Each piece is assigned to a machine in the cluster • Problem pieces should be loosely linked – Computation is faster than communication

PCs on a Campus • • Loosely coupled on a local-area-network PCs do other things some of the time When free cycles are available, they’re used Many more machines, but less of each machine available

Workstation Network at Google Front end 100 machines called www. google. com Searching machines Fit 40 -80 machines in a 7’x 2’x 3’ rack Retrieving machines

SETI • Telescope at Arecibo, PR collects data • Data is processed in real time by fast machines • But, no one looks for weak signals – Too costly • SETI@Home project built to do this

SETI@Home • Receive data from Arecibo – 35 Gbytes per day by snail mail • Break into Work Units –. 25 Mbyte each, so 140, 000 WU’s per day • WU takes 20 hours to process • Need about 117, 000 dedicated machines to process one day

SETI@Home • Get individual users to download software • Machine idle and screen saver runs software – Download WU – Compute – When finished send back result • Database at Berkeley reassembles results • Progress to date -- Seti@Home. Stats

Medical/Biological Applications • Peer-to-Peer Medicine • Cancer Research • …

Distributed databases • Data spread across machines in different ways – Web pages • E. g. HTTP – MP 3 collections • E. g. Napster, Gnutella • E. g Morpheus, Kazaa, Music City – Auction items • E. g. EBay

Client-Server Model • Central server • Clients store and retrieve data from server – File manager – HTTP

Napster Model • Server is only used to find who has the file • Communication is peer-to-peer (P 2 P) – Client to client transfer without a real server

How Napster works • Initial registration – name, password, local directory for files, … • When client connects to Napster server – Client provides list of files it will share – Napster updates its central index of available files • When client asks for a file – Napster gives client a list of online clients with that file

How Napster works (contd. ) • When client asks for download from given supplier – – Napster asks supplier to accept a request Napster tells client how to contact supplier Client opens port and fetches file from supplier Supplier and client report progress/completion status to Napster • Napster server directory continually updated • Client ranks potential servers by bandwidth and latency

Napster Model • Server is only used to make connections • Communication is peer-to-peer (P 2 P) – Client to client transfer without a real server • Can we do this without a central server? ? ?

Gnutella • Gnutella design has no central server • Every machine is both client and server (called servant in Gnutella) • To connect, you need to know any one machine already on the Gnutella network

How Gnutella works • To connect to the network, – only need to know of any servant that is already connected. – Your servant announces your presence to all of the servants it is already connected to, and so on until the message propagates throughout the entire network. – Each of these servants then responds to this message with a bit of information about itself: how many files it is sharing, how many KBs of space they take up, etc. • By connecting, you immediately know how much is available on the network to search through.

How Gnutella works - II • To search – You send out a search request, it is propagated through the network, and each servant that has matching terms passes back its result set – Each servant handles the search query in its own way – To save on bandwidth, a servant does not have to respond to a query if it has no matching items. The servant also has the option of returning only a limited result set.

How Gnutella works - III • For file sharing, each servant acts as a miniature HTTP web server. • To prevent searches from going on forever: – Gnutella messages have a TTL (Time To Live) – The TTL starts off at some low number, like 5 – Each time a packet is routed through a servant, the servant lowers the TTL by 1 – Once the TTL hits 0 the packet is no longer forwarded – Keeps messages from circling the network forever

What is Ka. Za. A (now Fast. Track) • Ka. Za. A Media Desktop 17 Million downloads of Ka. Za. A by April 2002! And 2 nd place on C|Net Download. com. Why don't you join the world's largest online media community right now. 91% of users are recommending it. What are you waiting for? Download it now - it's free. • Ka. Za. A Media Desktop is a full featured peer-to-peer file sharing application. You can search, download, organise and play your media files - audio, video, images and documents with it. It has a powerful search engine where you can search on 'meta data' such as categories, artist etc.

Users and Usage • 60 M users of file-sharing in US – 8. 5 M logged in at a given time on average • 814 M units of music sold in US last year – 140 M digital tracks sold by music companies • As of Nov, 35% of all Internet traffic was for Bit. Torrent, a single file-sharing system • Major legal battles underway between recording industry and file-sharing companies

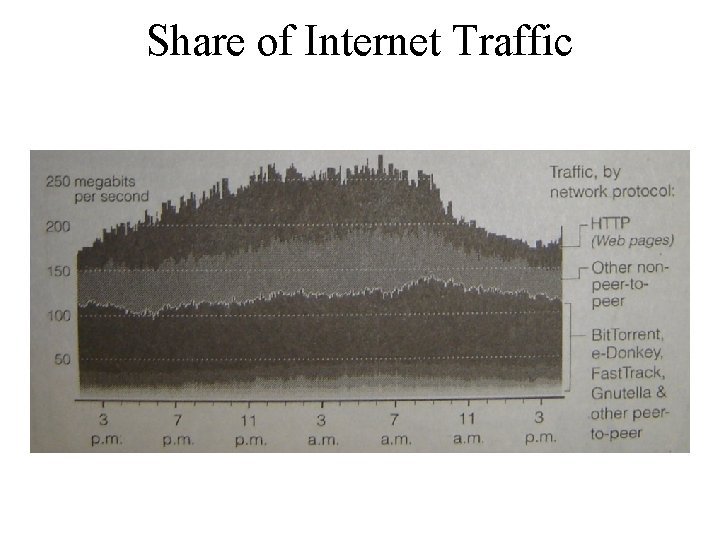
Share of Internet Traffic

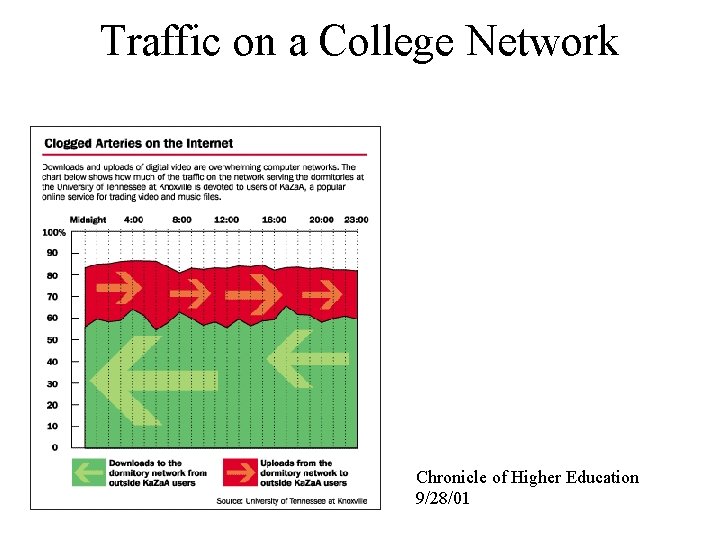
Traffic on a College Network Chronicle of Higher Education 9/28/01

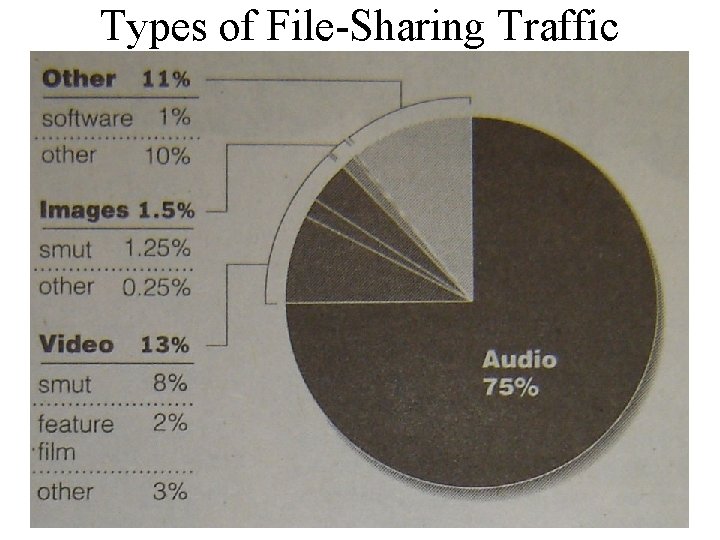
Types of File-Sharing Traffic

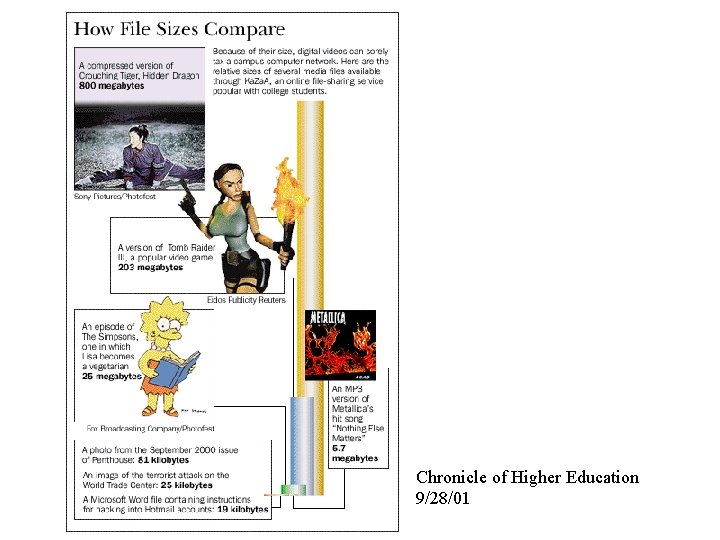
Chronicle of Higher Education 9/28/01

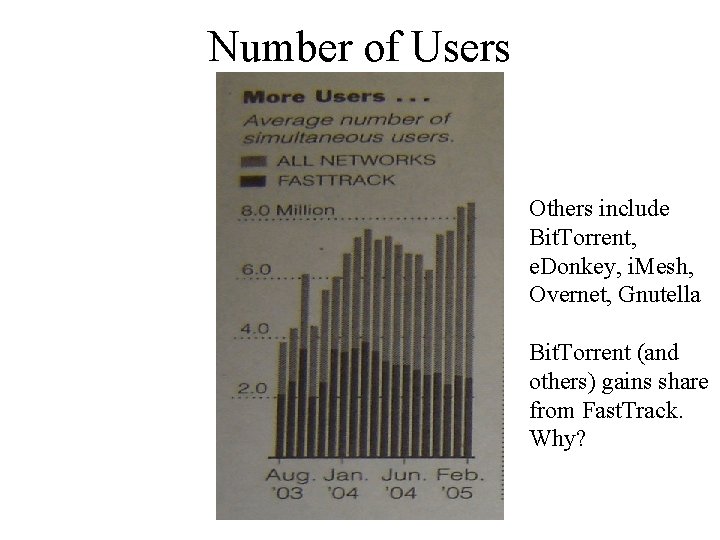
Number of Users Others include Bit. Torrent, e. Donkey, i. Mesh, Overnet, Gnutella Bit. Torrent (and others) gains share from Fast. Track. Why?

What about: • Copyrights – Who owns this stuff? – Why is this not like going to a store and stealing? • Breaches of trust – Try to download Friends but get pornography – Can download serious viruses • PU Bandwidth – This detracts from real work of the university?

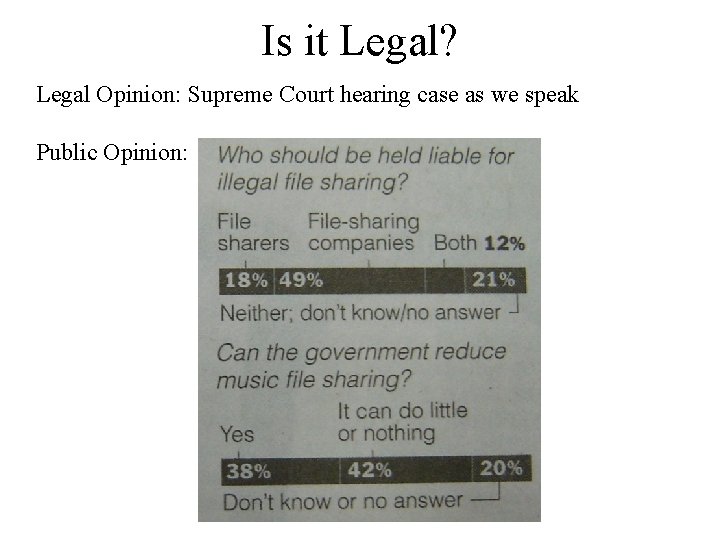
Is it Legal? Legal Opinion: Supreme Court hearing case as we speak Public Opinion:

What’s next • Problems for which there are no algorithms • Problems for which all algorithms run slowly • Applications of problems where algorithms run slowly

Hard problems

The big picture • • • We built a computer We built an operating system We attached the computer to a network We wrote programs We designed algorithms We looked at distributed algorithms and systems • Next, we want to see if there are limitations – Mathematical proofs that things cannot be done? ? ?

Simple unsolvable problem Consider the sentence: This sentence is false. Problem: Can you say, correctly, if the sentence is true or false?

Limitations of Computers? • Possible impossible tasks for computers? • Emotion • Creative thought • Beating the world chess champion? • Deep Blue v. Kasparov: Who won the 6 game rematch in 1997 • Others?

Limitations of Computers? • How to show that such tasks are impossible? • Find a cleanly defined problem • Prove a theorem that says it can’t be solved • Theorem is proved using axioms (like logic gates) that are assembled (like state machines and computers) to justify the result • The underlying field is called mathematical logic

Simple task --The “Hello” Assignment • You write a computer program which outputs “Hello!” and stops. • Assignment promises full credit for ANY program that outputs “Hello!” and then halts, and no credit otherwise. • Assignment is to be done on a computer that is as fast as you like and has as much memory as you like.

The “Hello” Assignment • Can I write a program that automatically grades your homework?

The “Hello” Assignment • Can I write a program that automatically grades your homework? • Sample program Function Grade. HELLO (Program P) Execute P, and store output in output If (output = “Hello!”) Then Return “Pass” Else Return “Fail” End If End Function

The “Hello” Assignment • Possible glitch – What if your homework program never stops? Program P Do While (1 > 0) Print “Hello!” End While End Program

The “Hello” Assignment Program P Do While (1 > 0) Print “Hello!” End While End Program • Student’s program runs forever! • This means the grading program would run forever. • It would never tell me that the student should fail…

The “Hello” Assignment I’m smarter than that: Can just stop the Program after 1 hour and fail the student if the program hasn’t stopped yet.

The “Hello” Assignment • What if student’s program stops, but takes a long time? Program P Initialize x = 0 Do While (x is not a proof of Fermat’s Last Theorem) x = next mathematical statement in a sequence End While Print “Hello!” End Program

The “Hello” Assignment • What if student’s program stops, but takes a long time? Program P Initialize x = 0 Do While (x is not a proof of Fermat’s Last Theorem) x = next mathematical statement in a sequence End While Print “Hello!” End Program • Grading program might say to fail you • But technically you deserve to Pass • Unless you never reach a statement that is the proof

The “Hello” Assignment • This is becoming a cat-and-mouse game… • Could it be that writing a computer program to grade such a simple assignment is impossible? • YES! Moreover we can prove that it is impossible.

The Halting Problem • Can we design a program, that tells whether other programs ever halt on given inputs? • Output of this program, called HALT, when applied to program P, is “halts” if P(input) eventually halts • Output of this program is “never halts” if P(input) never halts • Theorem (Alan Turing 1937): No computer program can solve the halting problem.

Proof by Contradiction • Assume the hypothesis to be proven is false, i. e. there is a computer program that can solve the halting problem • Show that this assumption leads to a contradiction • Do it by creating a program and an input to it that generate this contradiction