DISTRIBUSI PELUANG KONTINYU Ditribusi Normal Sebaran Normal Kurva

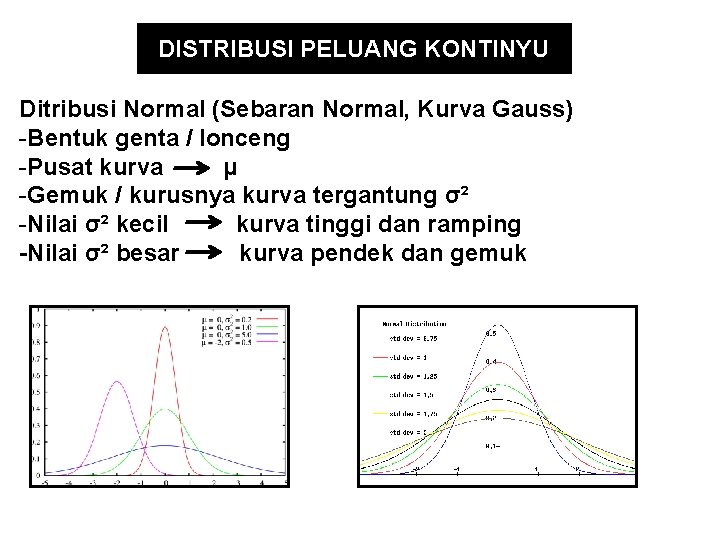
DISTRIBUSI PELUANG KONTINYU Ditribusi Normal (Sebaran Normal, Kurva Gauss) -Bentuk genta / lonceng -Pusat kurva μ -Gemuk / kurusnya kurva tergantung σ² -Nilai σ² kecil kurva tinggi dan ramping -Nilai σ² besar kurva pendek dan gemuk

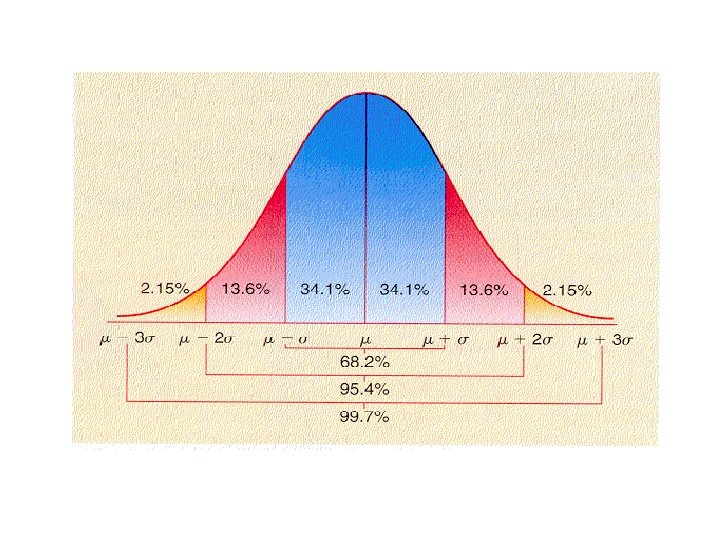
Peubah acak X ~ N (μ, σ²) μ (-∞ < μ < ∞ ) σ² > 0 Peubah tersebut mempunyai fungsi kepekatan : f (X) = ( 1 / √ 2 π σ² ) exp(- ½ σ² (x-μ) ………(1) Sebaran normal : 1. Luas daerah di bawah kurva = 1 2. f(x) > 0 untuk (-∞ < μ < ∞ ) 3. Lim f(x) = 0 dan lim f(x) 0 x ∞ x -∞ 4. f{(x)+ μ} = f {(x)- μ} atau kepekatan setangkup disekitar μ 5. Nilai maksimum f terjadi pada x = μ 6. Titik belok f terjadi pada x = μ ± σ

SEBARAN NORMAL BAKU Sebaran normal dibakukan/distandardkan : mempertimbangkan fungsi kepekatan : f(z) = (1/ √ 2 π) exp (- ½ z 2 ) …………. . (2) Hubungan antara sebaran 1 dan 2 adalah : x-μ Z= σ Contoh : Bobot badan kambing rataan μ = 25 kg, σ = 3 a. Berapa % bobot badan kambing yang lebih dari 29, 5 kg b. Berapa % bobot badan kambing yang kurang dari 28 kg c. Berapa % bobot kambing antara 24 – 27 kg

a. Z = (x- μ)/σ = (29, 5 -25)/3 = 1, 5 Z (1, 5) = 0, 4332 Bobot badan kambing > 29, 5 kg = 0, 5 -0, 4332 = 0, 0668 = 6, 68 % b. Z = (x- μ)/σ = (28 -25)/3 = 1, 0 Z (1, 0) = 0, 3413 Bobot badan kambing < 28 kg = 0, 5 + 0, 3413 = 0, 8413 = 84, 13 % c. Z = (x- μ)/σ = (24 -25)/3 = - 0, 33 Z(-0, 33) = 0, 1293 Z = (x- μ)/σ = (27 -25)/3 = 0, 67 Z(0, 67) = 0, 2486 Bobot badan kambing antara 24 -27 kg = 0, 1293 + 0, 2486 = 0, 3779 = 37, 79 %

Hipotesa : jawaban sementara terhadap masalah penelitian yang kebenarannya harus diuji secara empiris atau perumusan sementara mengenai sesuatu hal yang dibuat untuk menjelaskan hal tersebut dan mengarahkan penelitian selanjutnya Hipotesa nol (H 0) : hipotesa sementara sehingga memungkinkan untuk memutuskan apakah sesuatu yang diuji masih sebagaimana dispesifikasikan oleh Ho atau tidak. Hipotesa alternatif (H 1): alternatif dari H 0 yaitu keputusan apa yang harus ditentukan bila apa yang diuji tidak sebagaimana yang dispesifikasikan oleh H 0

Statistik uji : peubah acak yang digunakan dalam menentukan apakah H 0 atau H 1 yang diterima dalam pengujian hipotesa. Kriteria uji digunakan memutuskan diterima atau tidak H 0 disebut nilai- nilai kritis pengujian dipertimbangkan terletak di daerah penolakan. Pada pengujian hipotesa ada 2 jenis kesalahan : 1. Kesalahan jenis 1 : jika hipotesa nol (H 0) yang benar atau dianggap benar ditolak. Peluang untuk berbuat salah jenis 1 dilambangkan α dan umumnya disebut taraf nyata pengujian atau disebut ukuran uji

2. Kesalahan jenis 2 : jika hipotesa alternatif (H 1) yang benar ditolak. Peluang berbuat salah untuk kesalahan jenis 2 dilambangkan dengan β. Kesalahan jenis 2 dikaitkan dengan kekuatan uji. Pengujian hipotesa dengan sebaran normal baku Pengujian nilai tengah = rataan _ Z = (x - μ)/(σ/√n) H 0 : μ = μ 0 H 1 : μ ≠ μ 0 Jika H 0 benar, maka kaidah keputusannya adalah :

_ Z hitung = (x - μ)/(σ/√n) Z hitung > Z(α) H 0 ditolak H 1 diterima Z hitung < Z(α) H 0 diterima H 1 ditolak Contoh : Pengamatan pada kandungan Protein Kasar jerami padi diketahui : μ = 6 % σ = 1, 2 Apabila mahasiswa melakukan penelitian dari 25 sampel dan didapatkan kandungan PK jerami padi rataan = 6, 3 % Apakah hasil penelitian mahasiswa tersebut sama atau berbeda dengan pengamatan terdahulu, ujilah dengan α = 0, 05

Jawab: μ = 6 % σ = 1, 2 n = 25 _ x = 6, 3 α = 0, 05 H 0 : μ = 6 % H 1 : μ ≠ 6 % _ Z hitung = (x - μ)/(σ/√n) = (6, 3 – 6) / (1, 2/√ 25) = 1, 25 Z 0, 05/2 = 1, 96 Z hitung < Z 0, 05/2 1, 25 < 1, 96 H 0 diterima H 1 ditolak Kesimpulan : penelitian mahasiswa tentang kandungan PK jerami padi ternyata sama dengan data pengamatan terdahulu.

Contoh : Mahasiswa menyatakan bahwa kosentrat yang diproduksi oleh KUD Mitra tidak dapat meningkatkan PBB pada sapi rata-rata hanya 250 g/hari/ekor dengan σ = 25. Untuk menguji apakah pernyataan mahasiswa tersebut benar atau tidak, maka dilakukan pengamatan 25 ekor sapi dan diamati PBB didapatkan rata-rata = 260 g/hari/ekor. Ujilah dengan α = 0, 05 Jawab : μ = 250 σ = 25 n = 25 H 0 : μ < 250 H 1 : μ > 250 _ x = 260 α = 0, 05

_ Z hitung = (x - μ)/(σ/√n) = (260 – 250) / (25/√ 25) = 2 Z 0, 05 = 1, 645 Z hitung > Z 0, 05 2 > 1, 645 H 0 ditolak H 1 diterima Kesimpulan : pengamatan mahasiswa tersebut tidak benar karena kosentrat tersebut dapat meningkatkan PBB sapi

Pengujian Proporsi Untuk memudahkan pengujian hipotesa dapat dilakukan dengan pendekatan sebaran normal Z = (p 0 – p) / (√pq/n) q = 1 -p Merupakan peubah normal baku Hipotesa : H 0 : p = p 0 H 1 : p ≠ p 0 Jika H 0 benar, maka kaidah keputusannya adalah : Z hitung = (p 0 – p) / (√pq/n)

Z hitung > Z(α) H 0 ditolak H 1 diterima Z hitung < Z(α) H 0 diterima H 1 ditolak Contoh : Rataan berat lahir pedet sapi perah yang di bawah normal terdapat 10 ekor dari 100 ekor pedet yang lahir. Untuk mengetahui apakah pernyataan tersebut benar atau tidak dilakukan pengamatan pada pedet yang lahir dan ditimbang didapatkan 15 ekor yang berat lahirnya di bawah normal, ujilah dengan α = 0, 05.

Jawab : p = 10/100 = 0. 1 q = 1 -0, 1 = 0, 9 H 0 : p = 0, 1 H 1 : p ≠ 0, 1 p 0 = 15/100 = 0, 15 Z hitung = (p 0 – p) / (√pq/n) = (0, 15 -0, 1) / (√{(0, 1 x 0, 9)/100} = = 1, 67 Z 0, 05/2 = 1, 96 Z hitung < Z 0, 05/2 1, 67 < 1, 96 H 0 diterima H 1 ditolak Kesimpulan : Pernyataan tersebut benar bahwa berat lahir pedet tersebut yang di bawah normal sama dengan 10 %

Pengujian 2 nilai rataan 1. Ragam populasi diketahui Jika 2 populasi mempunyai rataan μA dan μB maka pada dasarnya menguji hipotesa nol : H 0 : μA = μB atau H 0 : μA – μB = 0 H 1 : μ A – μ B > 0 H 1 : μ A – μ B = 0 H 1 : μ A – μ B < 0 Peubah X XA ≈ NID (μA, σA 2 ) XB ≈ NID (μB, σB 2 ) _ _ (x. A- x. B) ≈ NID (μA- μB, σA 2/ n + σB 2/ n) Statistik uji, jika σA 2 dan σB 2 diketahui

_ _ Z hitung = {│(x. A- x. B) – (μA- μB)│} / √ (σA 2/ n + σB 2/ n) Jika H 0 : μA – μB = 0 benar maka : _ _ Z hitung = │(x. A- x. B)│ / √ (σA 2/ n + σB 2/ n) tersebar menurut sebaran normal Z Jika hipotesa : H 0 : μA – μB = 0 H 1 : μA – μB ≠ 0 H 0 benar maka kaidah keputasannya adalah jika : _ _ Z hitung = │(x. A- x. B)│ / √ (σA 2/ n + σB 2/ n)

Z hitung > Z(α) H 0 ditolak H 1 diterima Z hitung < Z(α) H 0 diterima H 1 ditolak Contoh : Pengamatan pada produksi susu sapi perah yang diberi pakan konsentrat A didapatkan rataan (x) = 10 l/ekor/hari dengan σ = 2, 5 n = 100. Sedangkan sapi yang diberi pakan konsentrat B didapatkan rataan (x) = 9 l/ekor/hari dengan σ = 1, 5 n = 100. Apakah produksi susu ke 2 kelompok tersebut sama atau berbeda, ujilah dengan α = 0, 05.

Jawab : _ x. A = 10 σA = 2, 5 σA 2 = 6, 25 n. A = 100 _ x. B = 9 σB = 1, 5 σA 2 = 2, 25 n. A = 100 _ _ Z hitung = (│(x. A- x. B)│) / √ (σA 2/ n + σB 2/ n) = (10 -9) / √ {(6, 25/100)+(2, 25/100)} = 3, 43 Z 0, 05/2 = 1, 96 Z hitung > Z 0, 05/2 Z hitung > Z(α) 3, 43 > 1, 96 H 0 ditolak H 1 diterima Kesimpulan : Produksi susu pada sapi yang diberi pakan konsentrat A berbeda dengan produksi susu sapi yang diberi pakan konsentrat B.