Distribusi Normal Berbentuk lonceng Simetris fX Mean Median

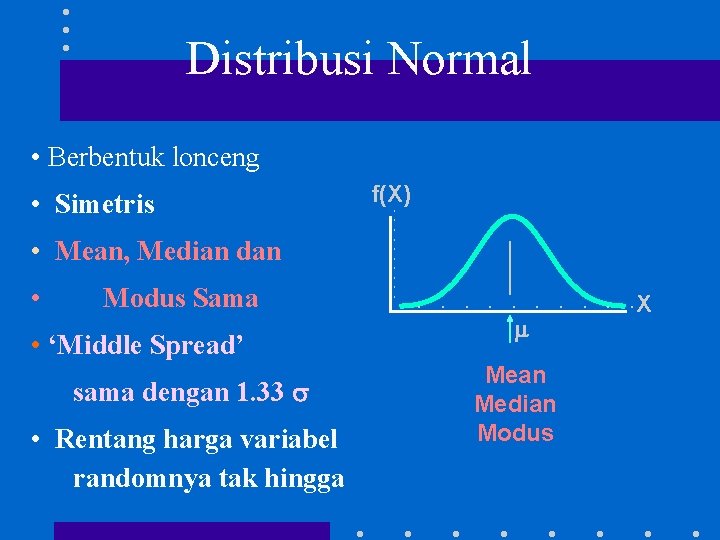
Distribusi Normal • Berbentuk lonceng • Simetris f(X) • Mean, Median dan • Modus Sama • ‘Middle Spread’ sama dengan 1. 33 • Rentang harga variabel randomnya tak hingga Mean Median Modus X

Model Matematis f(X) = 1 2 e (-1/2)((X- ) frekuensi variabel random X (fungsi densitas probabilitas X) = 3. 14159; = deviasi standar populasi X = harga variabel random (- < X < ) = mean populasi e = 2. 71828

Banyaknya Distribusi Normal Ada tak hingga banyak Setiap harga parameter and tertentu, menentukan suatu Distribusi Normal

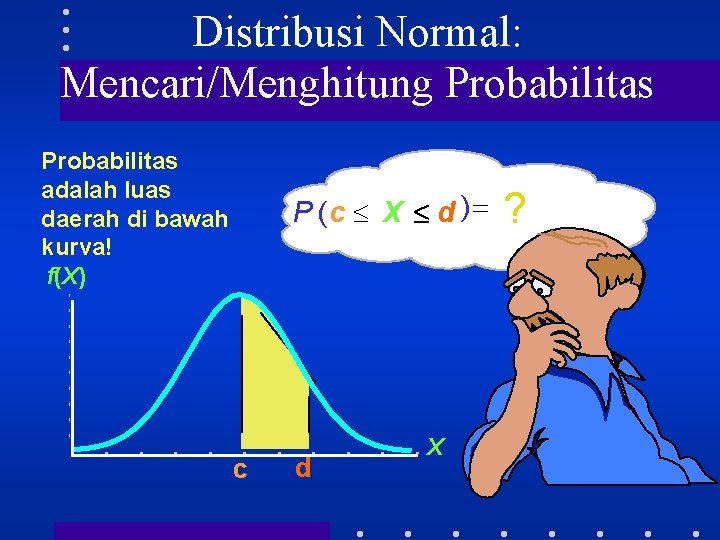
Distribusi Normal: Mencari/Menghitung Probabilitas adalah luas daerah di bawah kurva! f(X) P (c X d ) c d X ?

Tabel untuk Menghitung? Apakah setiap distribusi harus punya tabel sendiri? Tak hingga banyak distribusi normal berarti Harus ada tak hingga banyak tabel. No way!!

Distribusi Normal Standar Tabel probabilitas distribusi normal standar (sebagian) Z . 00 . 01 Z = 0 and Z = 1. 0478 . 02 0. 0. 0000. 0040. 0080 0. 1. 0398. 0438. 0478 0. 2. 0793. 0832. 0871 Z = 0. 12 0. 3. 0179. 0217. 0255 Probabilitas Shaded Area Exaggerated

Contoh Standardizing Distribusi Normal Standar = 10 Z = 1 = 5 6. 2 X = 0. 12 Shaded Area Exaggerated Z

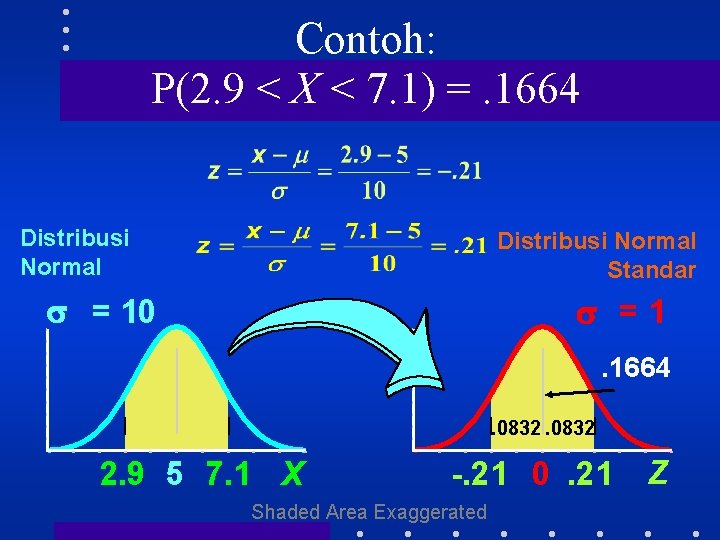
Contoh: P(2. 9 < X < 7. 1) =. 1664 Distribusi Normal Standar = 10 =1. 1664. 0832 2. 9 5 7. 1 X -. 21 0. 21 Shaded Area Exaggerated Z

Contoh: P(X 8) =. 3821. Distribusi Normal Standardized Normal Distribution = 10 =1. 5000. 1179 =5 8 X . 3821 = 0. 30 Z Shaded Area Exaggerated

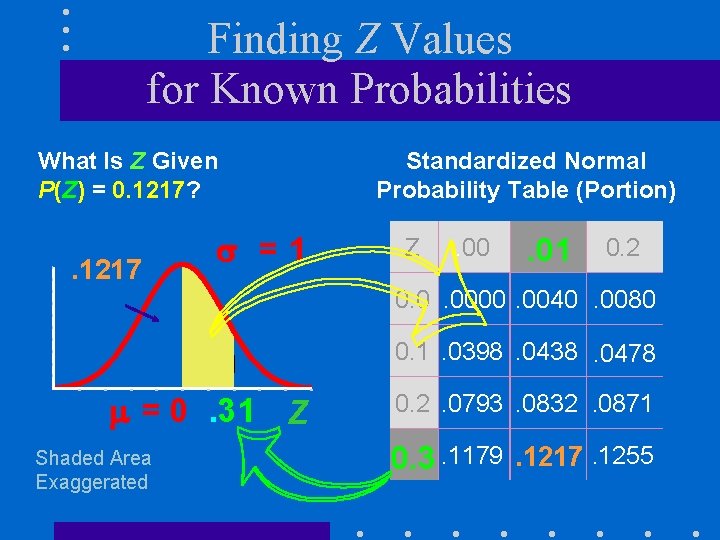
Finding Z Values for Known Probabilities What Is Z Given P(Z) = 0. 1217? . 1217 =1 Standardized Normal Probability Table (Portion) Z . 00 . 01 0. 2 0. 0. 0000. 0040. 0080 0. 1. 0398. 0438. 0478 = 0. 31 Z Shaded Area Exaggerated 0. 2. 0793. 0832. 0871 0. 3. 1179. 1217. 1255

Finding X Values for Known Probabilities Normal Distribution Standardized Normal Distribution = 10 =1. 1217 =5 ? X . 1217 = 0. 31 X Z = 5 + (0. 31)(10) = 8. 1 Shaded Area Exaggerated Z