Distribusi Normal Berbentuk lonceng n Simetris fx n

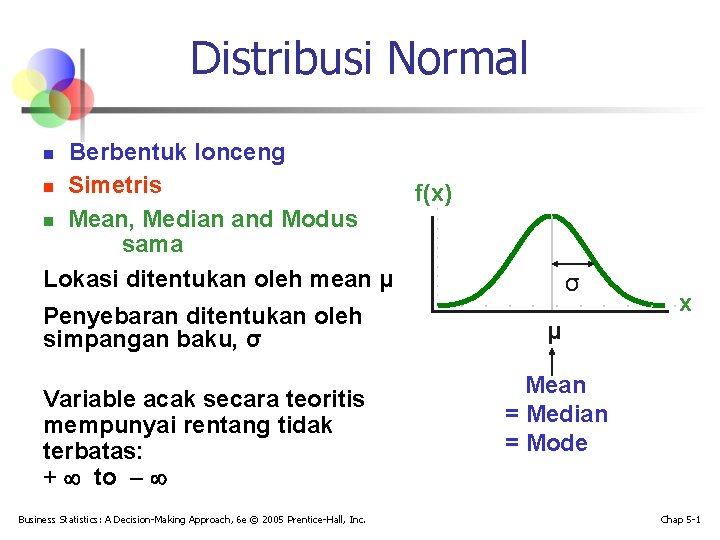
Distribusi Normal ‘Berbentuk lonceng’ n Simetris f(x) n Mean, Median and Modus sama Lokasi ditentukan oleh mean μ n Penyebaran ditentukan oleh simpangan baku, σ Variable acak secara teoritis mempunyai rentang tidak terbatas: + to Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. σ x μ Mean = Median = Mode Chap 5 -1

Dengan mengubah parameter μ and σ, dapat diperoleh distirbusi normal yang berbeda

Bentuk Distributsi Normal f(x) Pengubahan μ menggeser distribusi ke kiri atau ke kanan. σ μ Pengubahan σ menaikkan atau menurunkan penyebaran. x

Mencari Probabilitas Normal Probability is the Probabilitas diukur menggunakan area under the curve! daerah di bawah kurva f(x) luas P (a x b) a b x

Probabilitas sebagai Luas Daerah di Bawah Kurva Total luas daerah di bawah kurva adalah 1. 0 Kurva simetris sehingga setengahnya di atas mean (rata-rata) dan setengahnya di bawah mean f(x) 0. 5 μ x

Aturan Empiris Aturan umum distribusi nilai di sekitar mean f(x) μ ± 1σ mencakup sekitar 68% dari x σ μ 1σ σ μ μ+1σ 68. 26% x

n μ ± 2σ mencakup sekitar 95% dari x n μ ± 3σ mencakup sekitar 99. 7% dari x 2σ 3σ 2σ μ x 95. 44% Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 3σ μ x 99. 72% Chap 5 -7

Diastirbusi Normal Standar n n n Juga disebut sebagai distirbusi “z” Mean = 0 Simpangan baku = 1 f(z) 1 0 z Nilai di atas mean mempunyai nilai z positif Nilai di bawah mean mempunyai nilai z negatif

n n Semua distribusi normal (dengan kombinasi mean dan simpangan baku apapun) dapat diubah ke dalam distribusi normal standar (z) x diubah ke dalam z

Pengubahan ke dalam Diatribusi Normal Standar n Ubah dari x ke dalam normal standar (distirbusi “z”) dengan mengurangkan mean dari x and membaginya dengan simpangan baku:

Contoh: n n Jika x didistribusikan secara normal dengan mean 100 dan simpangan baku 50, maka nilai z value untuk x = 250 adalah x = 250 merupakan 3 simpangan baku (meningkat 3 kali 50 unit) di atas mean 100.

Membandingkan x and z μ = 100 σ = 50 100 0 250 3. 0 x z Distribusi tetap sama, tetapi skalanya berbeda. Permasalahan dapat dinyatakan dalam bentuk asli (x) atau dalam bentuk yang distandarkan (z)

Tabel Normal Standar n Tabel Normal Standar memberikan probabilitas dari mean (0) hingga nilai z yang diinginkan . 4772 Contoh: P(0 < z < 2. 00) =. 4772 0 2. 00 z

Kolom menunjukkan nilai z hingga 2 desimal Baris menunjukkan nilai z hingga 1 desimal . . . 2. 0 . 4772 P(0 < z < 2. 00)2. 0 =. 4772 Nilai dalam tabel menunjukkan probabilitas dari z = 0 hingga nilai z yang diinginkan

Prosedur Umum untuk Memperoleh Probabilitas Untuk memperoleh P(a < x < b) jika x didistribusikan secara normal: n n n Digambar kurva normal dalam bentuk x Ubah nilai x ke dalam nilai z Gunakan Tabel Normal Standar

Contoh Tabel Z n Jika x normal dengan mean 8. 0 dan simpangan baku 5. 0. Cari P(8 < x < 8. 6) Hitung nilai z: 8 8. 6 x 0 0. 12 Z P(8 < x < 8. 6) = P(0 < z < 0. 12)

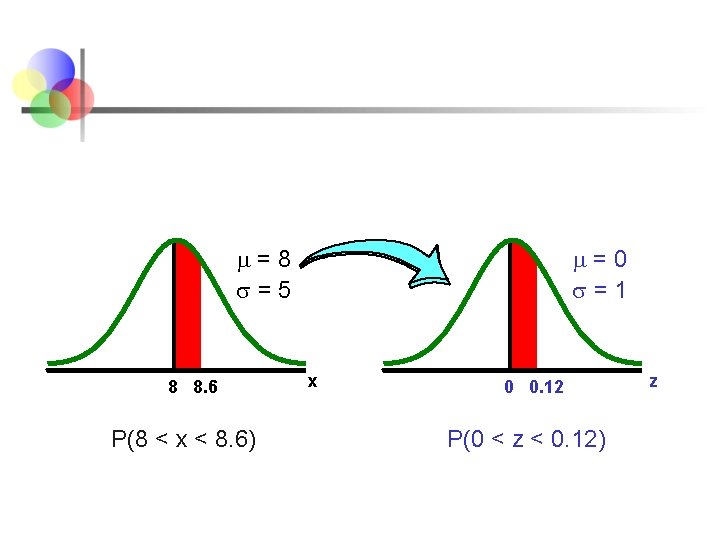
m=8 =5 8 8. 6 P(8 < x < 8. 6) m=0 =1 x 0 0. 12 P(0 < z < 0. 12) z

Penyelesaian: P(0 < z < 0. 12) Tabel Probabilitas Normal Standar z . 00 . 01 P(8 < x < 8. 6) = P(0 < z < 0. 12) . 02 . 0478 0. 0. 0000. 0040. 0080 0. 1. 0398. 0438. 0478 0. 2. 0793. 0832. 0871 0. 3. 1179. 1217. 1255 0. 00 0. 12 Z

Mencari Probabilitas Normal Jika x normal dengan mean 8. 0 dan simpangan baku 5. 0. n Cari P(x < 8. 6) n Z 8. 0 8. 6

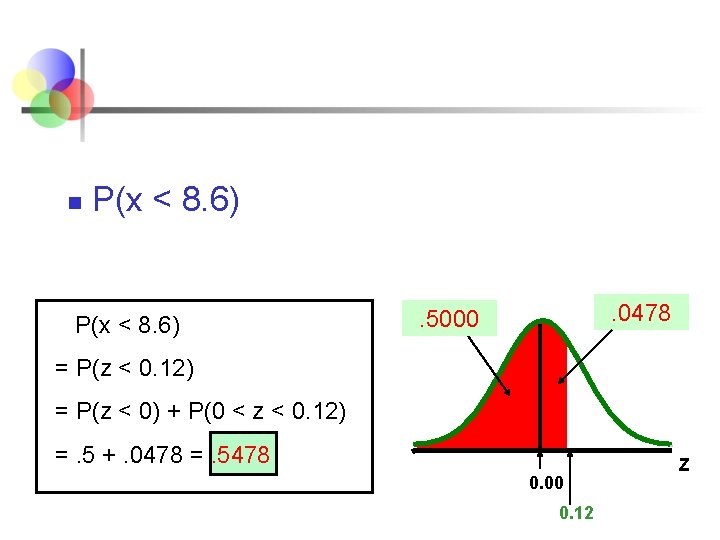
n P(x < 8. 6) . 0478 . 5000 = P(z < 0. 12) = P(z < 0) + P(0 < z < 0. 12) =. 5 +. 0478 =. 5478 0. 00 0. 12 Z

Probabilitas pada Ekor Atas Jika x normal dengan mean 8. 0 dan simpangan baku 5. 0. n Cari P(x > 8. 6) n Z 8. 0 8. 6

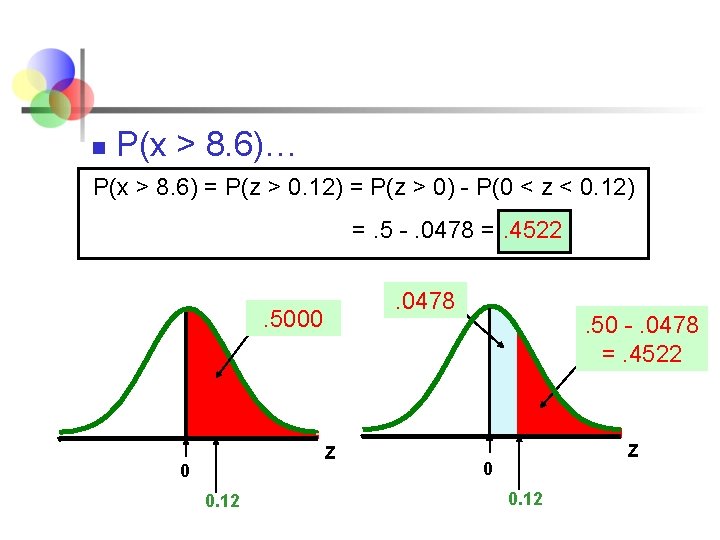
n P(x > 8. 6)… P(x > 8. 6) = P(z > 0. 12) = P(z > 0) - P(0 < z < 0. 12) =. 5 -. 0478 =. 4522. 0478 . 5000 Z 0 0. 12 . 50 -. 0478 =. 4522 Z 0 0. 12

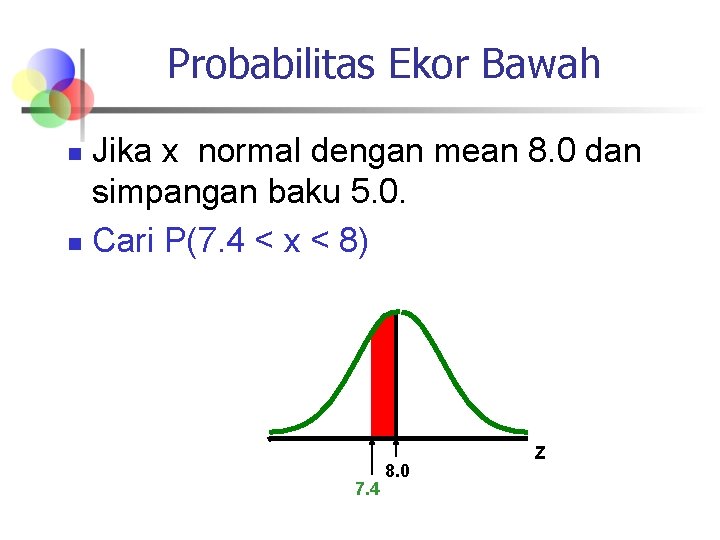
Probabilitas Ekor Bawah Jika x normal dengan mean 8. 0 dan simpangan baku 5. 0. n Cari P(7. 4 < x < 8) n 7. 4 8. 0 Z

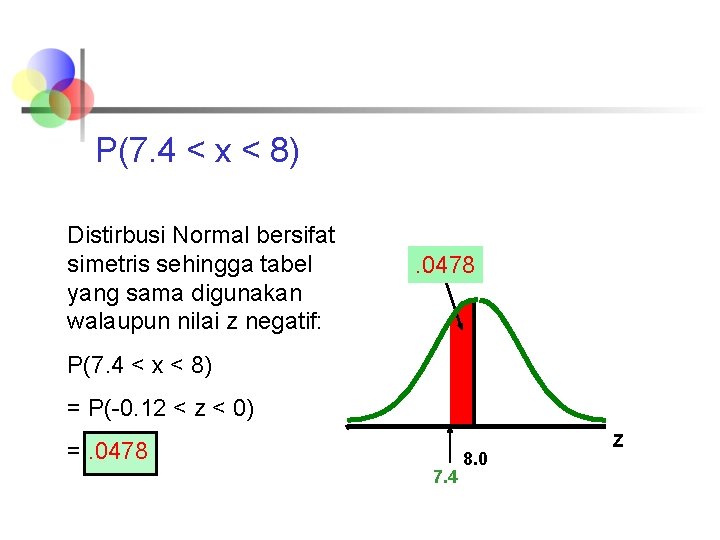
P(7. 4 < x < 8) Distirbusi Normal bersifat simetris sehingga tabel yang sama digunakan walaupun nilai z negatif: . 0478 P(7. 4 < x < 8) = P(-0. 12 < z < 0) =. 0478 7. 4 8. 0 Z

Mencari Nilai X untuk Probabilitas yang Diketahui n Langkah: 1. Cari nilai Z untuk probabilitas yang diketahui 2. Ubah ke dalam bentuk X dengan rumus:

Contoh: n Jika X terdistribusi normal dengan mean 8. 0 dan simpangan baku 5. 0. n Berapakah nilai X sehingga 20% dari data Anda berada di bawah nilai X tersebut? 0. 2000 ? ? 8. 0 0 X Z

Jawab: 1. Cari nilai Z untuk probabilitas yang diketahui n Z 0. 7 … . 03 . 04 . 05 20% daerah di ekor bawah mempunyai nilai Z -0. 84 …. 2673. 2703. 2734 0. 8 …. 2967. 2995. 3023 0. 9 …. 3238. 3264. 3289 0. 2000 ? 8. 0 -0. 84 0 X Z

2. Ubah ke dalam bentuk X dengan rumus: Jadi, 20% dari data Anda yang terdistirbusi normal dengan mean 8. 0 dan simpangan baku 5. 0 berada di bawah 3. 80

Distribusi Seragam n Distribusi seragam merupakan sebuah distribusi probabilitas yang mempunyai probabilitas yang sama untuk seluruh hasil yang mungkin dari variabel acak

Distribusi seragam kontinyu: f(x) = nilsi fungsi densitas (kepadatan) pada nilai x a = batas bawah interval b = batas interval

Nilai X yang diharapkan E(X) = (a + b)/2 Variansi X Var(X) = (b - a)2/12

Contoh: Pelanggan rata-rata membeli 2 -6 kg beras per minggu. Buatlah probabilty density function (fungsi kepadatan / densitas probabilitas) untuk kuantitas beras yang dibeli pelanggan. Berapakah probabilitas bahwa beras yang dibeli antara 4 -6 kg?

1 f(x) = 6 - 2 =. 25 for 2 ≤ x ≤ 6 f(x). 25 2 6 x

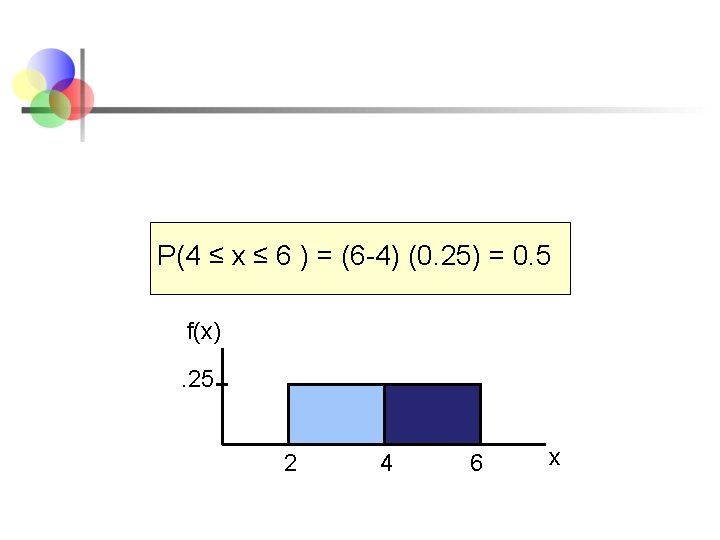
P(4 ≤ x ≤ 6 ) = (6 -4) (0. 25) = 0. 5 f(x). 25 2 4 6 x

Berapakah P(3 ≤ X ≤ 5): P(3 ≤ X ≤ 5) = (Dasar)(Tinggi) = (2)(0. 25) = 0. 5 f(X) 0. 25 2 3 4 5 6 X

Distribusi Eksponensial n Digunakan untuk mengukur waktu antara dua kejadian n Contoh: n Waktu antara kedatangan 2 truk di tempat pembongkaran muatan n Waktu antara kedatangan bahan baku n Waktu antara pemesanan produk dari pelanggan

n Probability Density Function (pdf): n n x ≥ 0 dan μ>0. μ mean atau nilai yang diharapkan.

Bentuk lain: μ =

n n Hanya mempunyai 1 parameter, yaitu mean (= λ) Probabilitas bahwa suatu kejadian kurang dari waktu tertentu X adalah: e = 2. 71828 λ = jumlah kejadian periode waktu = mean populasi 1/ adalah rata-rata (mean) waktu antara kejadian X = nilai variabel kontinyu 0 < X <

Jika banyaknya kejadian periode waktu terdistribusi Poisson dengan mean , maka waktu antar kejadian terdistribusi eksponensial dengan rata-rata waktu 1/ Contoh: Jika rata-rata 10 pelanggan mengunjungi sebuah restoran dalam 2 jam, maka waktu rata-rata antar kedatangan pelanggan adalah: 120/10=12 minutes. Oleh karena itu, interval waktu antar kedatangan pelanggan terdistribusi eksponensial dengan mean=12 minutes.

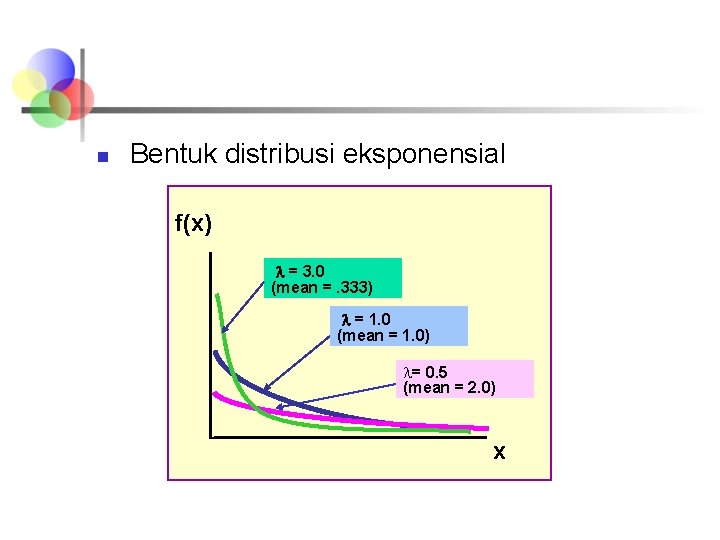
n Bentuk distribusi eksponensial f(x) = 3. 0 (mean =. 333) = 1. 0 (mean = 1. 0) = 0. 5 (mean = 2. 0) x

Contoh Pelanggan datang dengan laju 15 orang per jam (terdistribusi Poisson). Berapa probabilitas bahwa waktu kedatangan antar pelanggan secara berturutan kurang dari 5 menit? § P(x < 5) = 1 - e- x = 1 – e-(. 25)(5) =. 7135

Daya ingat yang terbatas n n n Distribusi eksponensial mempunyai sifat “Memorylessness” atau “Lack of memory”. Dalam bentuk matematika: Contoh: P(menunggu lebih dari 10 menit | menunggu lebih dari 3 menit) =P(menunggu lebih dari 7+3 menit | menunggu lebih dari 3 menit) =P(menunggu lebih dari 7 menit)

Mean dan Variansi Distirbusi Eksponensial n E(X)= μ or n Var(X)= μ 2 or