Distribusi Frekuensi Pengertian Susunan data menurut kelaskelas interval

Distribusi Frekuensi

Pengertian Susunan data menurut kelas-kelas interval tertentu atau menurut kategori tertentu dalam sebuah daftar Dari distribusi frekuensi dapat diperoleh keterangan atau gambaran sederhana dan sistematis dari data yang diperoleh.

Bagian-bagian distribusi frekuensi Kelas-kelas (class) Batas kelas (class limits) Tepi kelas (class boundary) Titik tengah kelas/tanda kelas (class mid point/class marks) Interval kelas (class interval) Panjang Interval kelas atau kelas (interval kelas) Frekuensi kelas (class frequency)

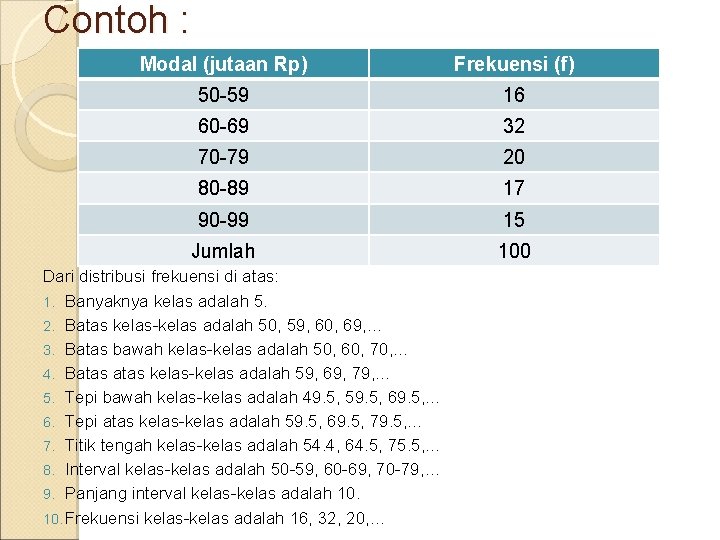
Contoh : Modal (jutaan Rp) Frekuensi (f) 50 -59 16 60 -69 32 70 -79 20 80 -89 17 90 -99 15 Jumlah 100 Dari distribusi frekuensi di atas: 1. Banyaknya kelas adalah 5. 2. Batas kelas-kelas adalah 50, 59, 60, 69, … 3. Batas bawah kelas-kelas adalah 50, 60, 70, … 4. Batas kelas-kelas adalah 59, 69, 79, … 5. Tepi bawah kelas-kelas adalah 49. 5, 59. 5, 69. 5, … 6. Tepi atas kelas-kelas adalah 59. 5, 69. 5, 79. 5, … 7. Titik tengah kelas-kelas adalah 54. 4, 64. 5, 75. 5, … 8. Interval kelas-kelas adalah 50 -59, 60 -69, 70 -79, … 9. Panjang interval kelas-kelas adalah 10. Frekuensi kelas-kelas adalah 16, 32, 20, …

Penyusunan Distribusi Frekuensi Mengurutkan data dari yang terkecil ke yang terbesar. 2. Menentukan jangkauan (range) dari data. 1. Jangkauan = data terbesar – data terkecil 3. Menentukan banyaknya kelas (k). k = 1 + 3. 3 log n; k Є bulat ket : k = banyaknya kelas n = banyaknya data Hasil dibulatkan, biasanya ke atas. Menentukan panjang interval kelas. Panjang interval kelas (i) = jangkauan (R) / banyaknya kelas (k) 5. Menentukan batas bawah kelas pertama. 6. Menuliskan frekuensi kelas secara melidi dalam kolom turus sesuai banyaknya data. 4.

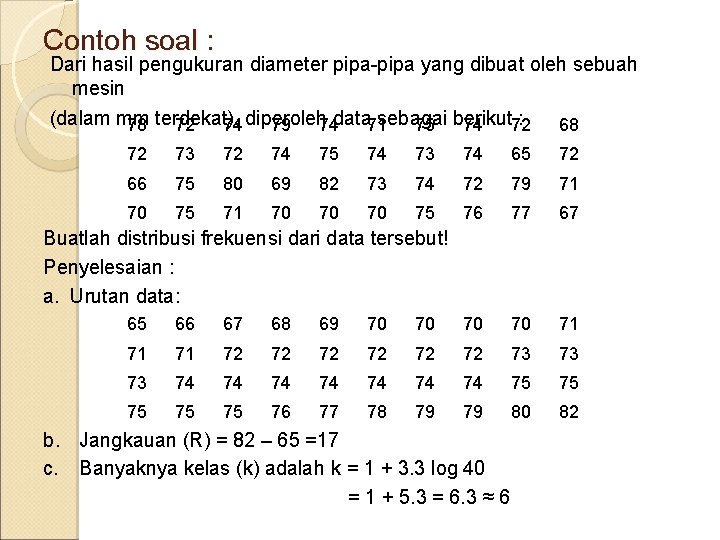
Contoh soal : Dari hasil pengukuran diameter pipa-pipa yang dibuat oleh sebuah mesin (dalam mm sebagai : 78 terdekat), 72 74 diperoleh 79 74 data 71 75 berikut 74 72 68 72 73 72 74 75 74 73 74 65 72 66 75 80 69 82 73 74 72 79 71 70 75 71 70 70 70 75 76 77 67 Buatlah distribusi frekuensi dari data tersebut! Penyelesaian : a. Urutan data: 65 66 67 68 69 70 70 71 71 71 72 72 72 73 73 73 74 74 75 75 75 76 77 78 79 79 80 82 b. Jangkauan (R) = 82 – 65 =17 c. Banyaknya kelas (k) adalah k = 1 + 3. 3 log 40 = 1 + 5. 3 = 6. 3 ≈ 6

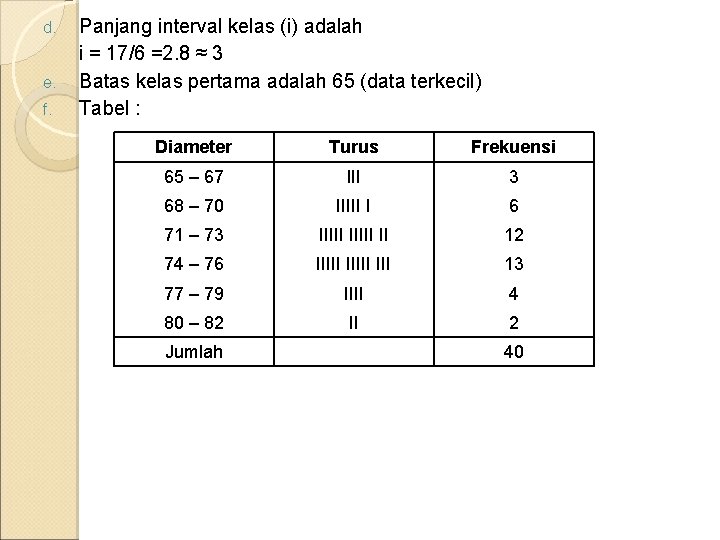
d. e. f. Panjang interval kelas (i) adalah i = 17/6 =2. 8 ≈ 3 Batas kelas pertama adalah 65 (data terkecil) Tabel : Diameter Turus Frekuensi 65 – 67 III 3 68 – 70 IIIII I 6 71 – 73 IIIII II 12 74 – 76 IIIII III 13 77 – 79 IIII 4 80 – 82 II 2 Jumlah 40

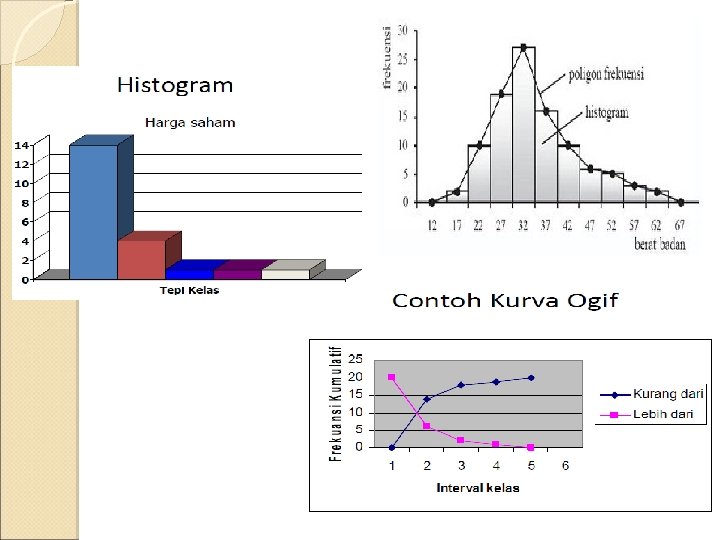
Histogram, Poligon, Frekuensi, dan Kurva Histogram dan Poligon Frekuensi Histogram dan poigon frekuensi adalah dua grafik yang sering digunakan untuk menggambarkan distribusi frekuensi. Histogram merupakan grafik batang dari distribusi frekuensi dan poligon frekuensi merupakan grafik garisnya. Batang-batang pada histogram saling melekat atau berimpitan. Poligon frekuensi dibuat dengan cara menarik garis dari satu titik tengah batang histogram ke titiktengah batang histogram yang lain. Pada pembuatan histogram digunakan sistem salin sumbu. Sumbu-sumbu mendatar (sumbu X) menyatakan interval kelas (tepi bawah kelas dan tepi

Histogram, Poligon, Frekuensi, dan Kurva Bentuk Kurva Frekuensi Simetris atau berbentuk lonceng, cirinya ialah nilai variabel di samping kiri dan kanan yang berjarak sama terhadap titik tengah (frekuensi terbesar) mempunyai frekuensi yang sama. Dinamakan juga distribusi normal. Tidak simetris/condong. Condong ke kanan (kocondongan positif) , Condong ke kiri (kecondongan negatif).

Histogram, Poligon, Frekuensi, dan Kurva Bentuk Kurva Frekuensi Bentuk J atau J terbalik, ciri-cirinya ialah satu nilai ujung kurva memiliki frekuensi maksimum. Bentuk U, dengan ciri kedua ujung kurva memiliki frekuensi maksimum. Bimodal, dengan ciri mempunyai dua maksimal. Multimodal, dengan ciri mempunyai lebih dari dua maksimal. Uniform, terjadi bila nilai-nilai variabel dalam suatu interval mempunyai frekuensi yang sama.

Jenis-jenis Distribusi Frekuensi Biasa adalah distribusi frekuensi ysng hanya berisikan jumlah frekuensi dari setiap kelompok data atau kelas. Jenis DFB: üDistribusi Frekuensi Numerik adalah distribusi frekuensi yang pembagian kelasnya dinyatakan dalam angka. Contoh : Tabel Frekuensi pelamar suatu perusahaan berdasarkan umur. üDistribusi Frekuensi Peristiwa atau kategori adalah yang pembagian kelasnya dinyatakan berdasarkan data atau golongan data yang ada. Contoh : Tabel banyaknya peristiwa pada hasil pelemparan dadu berdasarkan anga dadu.

Jenis-jenis Distribusi Frekuensi Relatif adalah distribusi frekuensi yang berisikan nilai-nilai hasil bagi antara frekuensi kelas dan jumlah pengamatan yang terkandung dalam kumpulan data yang terdistribusi tertentu. Rumus :

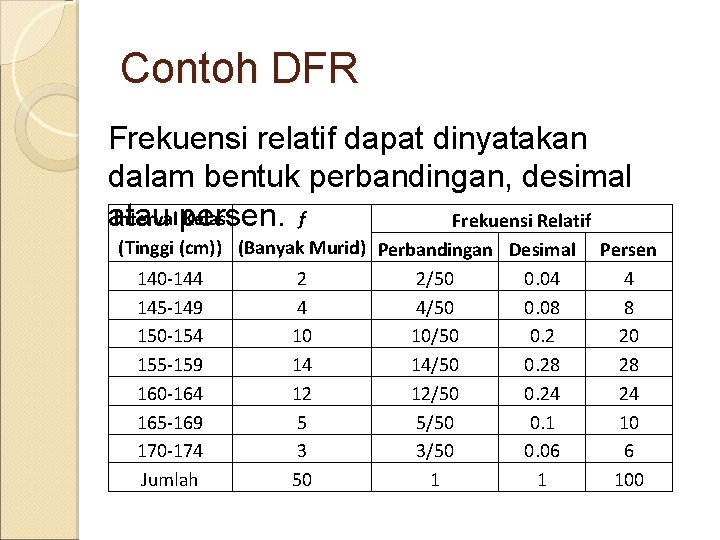
Contoh DFR Frekuensi relatif dapat dinyatakan dalam bentuk perbandingan, desimal Interval persen. Kelas f atau Frekuensi Relatif (Tinggi (cm)) (Banyak Murid) Perbandingan Desimal 140 -144 2 2/50 0. 04 145 -149 4 4/50 0. 08 150 -154 10 10/50 0. 2 155 -159 14 14/50 0. 28 160 -164 12 12/50 0. 24 165 -169 5 5/50 0. 1 170 -174 3 3/50 0. 06 Jumlah 50 1 1 Persen 4 8 20 28 24 10 6 100

Jenis-jenis Distribusi Frekuensi Kumulatif Adalah distribusi frekuensi yang berisikan frekuensi kumulatif. Frekuensi kumulatif adalah frekuensi yang dijumlahkan. Distribusi frekuensi kumulatif memiliki grafik atau kurva yang disebut ogif. Jenis DFK ü Distribusi Frekuensi Kumulatif Kurang Dari adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai kurang dari nilai batas kelas suatu interval tertentu. ü Distribusi Frekuensi Kumulatif Lebih Dari adalah distribusi frekuensi yang memuat jumlah frekuensi yang memiliki nilai lebih dari nilai batas kelas suatu interval tertentu.

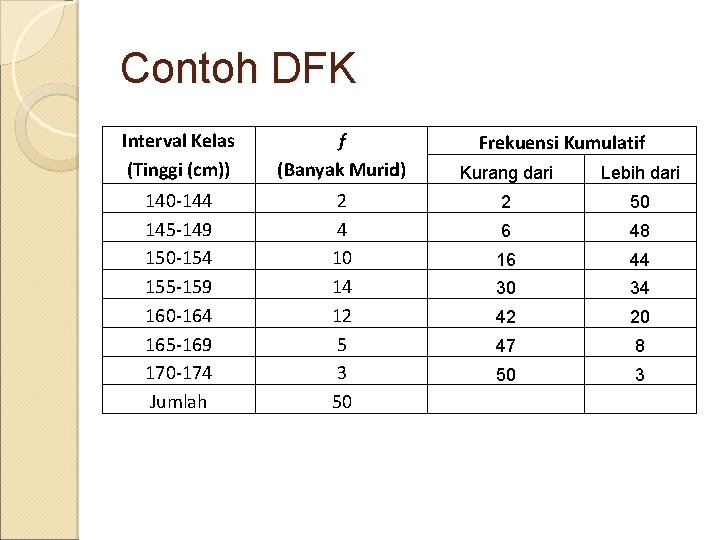
Contoh DFK Interval Kelas (Tinggi (cm)) f (Banyak Murid) 140 -144 145 -149 150 -154 155 -159 160 -164 165 -169 170 -174 Jumlah 2 4 10 14 12 5 3 50 Frekuensi Kumulatif Kurang dari Lebih dari 2 50 6 48 16 44 30 34 42 20 47 8 50 3