DISTRIBUCIONES BIDIMENSIONALES Tema 12 Angel Prieto Benito Matemticas

DISTRIBUCIONES BIDIMENSIONALES Tema 12 @ Angel Prieto Benito Matemáticas Aplicadas CS I 1

TABLAS DE DOBLE ENTRADA Tema 12. 1 * 1º BCS @ Angel Prieto Benito Matemáticas Aplicadas CS I 2

Tablas de doble entrada xi yi 39 40 41 42 15 130 90 60 50 16 75 110 95 65 17 55 70 80 120 xi=Edad de las personas de la muestra yi=Número de calzado de las personas de la muestra. n=130+90+60+50+75+110+95+65+55+70+80+120 = 1000 personas Para estudiarlo como hasta ahora necesitaríamos una tabla de 1000 filas. La tabla de tabulación pasa a ser tabla de frecuencias. @ Angel Prieto Benito Matemáticas Aplicadas CS I 3

Tablas de doble entrada xi yi 39 40 41 42 15 130 90 60 50 16 75 110 95 65 17 55 70 80 120 @ Angel Prieto Benito Matemáticas Aplicadas CS I 4

Parámetros • En una distribución bidimensional existen los siguientes parámetros a calcular: • • MEDIA MARGINAL de xi: Es la media respecto de xi. x = ∑ xi. fi / ∑ fi • • MEDIA MARGINAL de yi: Es la media respecto de yi. y = ∑ yi. fi / ∑ fi • Al punto (x, y) se le llama centro de gravedad de la distribución. • • DESVIACIÓN TÍPICA MARGINAL de xi: sx = √ [ ( ∑ fi. xi 2 / ∑ fi ) – x 2 ] • • DESVIACIÓN TÍPICA MARGINAL de yi: sy = √ [ ( ∑ fi. yi 2 / ∑ fi ) – y 2 ] @ Angel Prieto Benito Matemáticas Aplicadas CS I 5

• COVARIANZA: Es un parámetro estadístico conjunto. • ∑ fi. xi. yi • Vxy = ----- - x. y • xy ∑ fi • COEFICIENTE DE CORRELACIÓN LINEAL • Igual que sin doble entrada. • COEFICIENTE DE DETERMINACIÓN • Igual que sin doble entrada. • RECTAS DE REGRESIÓN O AJUSTE • Igual que sin doble entrada. @ Angel Prieto Benito Matemáticas Aplicadas CS I 6

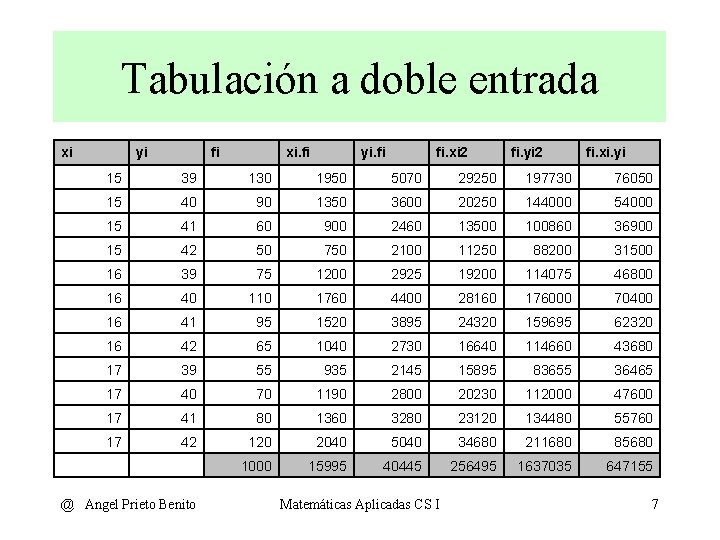
Tabulación a doble entrada xi yi fi xi. fi yi. fi fi. xi 2 fi. yi 2 fi. xi. yi 15 39 130 1950 5070 29250 197730 76050 15 40 90 1350 3600 20250 144000 54000 15 41 60 900 2460 13500 100860 36900 15 42 50 750 2100 11250 88200 31500 16 39 75 1200 2925 19200 114075 46800 16 40 110 1760 4400 28160 176000 70400 16 41 95 1520 3895 24320 159695 62320 16 42 65 1040 2730 16640 114660 43680 17 39 55 935 2145 15895 83655 36465 17 40 70 1190 2800 20230 112000 47600 17 41 80 1360 3280 23120 134480 55760 17 42 120 2040 5040 34680 211680 85680 1000 15995 40445 256495 1637035 647155 @ Angel Prieto Benito Matemáticas Aplicadas CS I 7

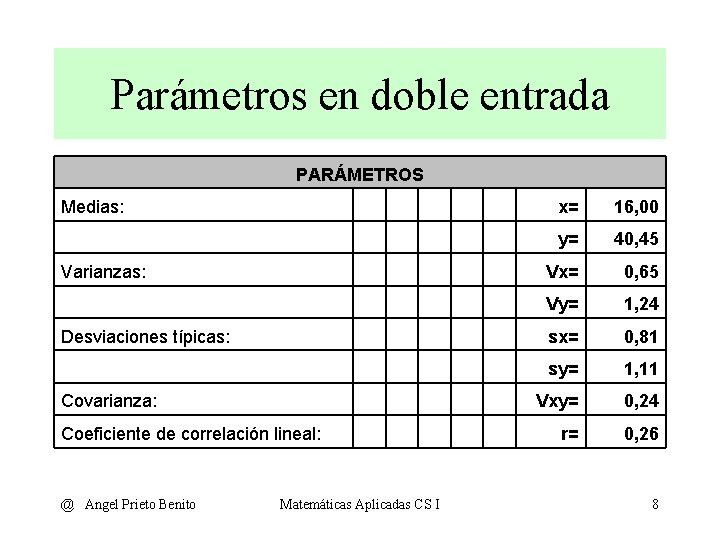
Parámetros en doble entrada PARÁMETROS Medias: x= 16, 00 y= 40, 45 Varianzas: Vx= 0, 65 Vy= 1, 24 Desviaciones típicas: sx= 0, 81 sy= 1, 11 Covarianza: Vxy= 0, 24 Coeficiente de correlación lineal: r= 0, 26 @ Angel Prieto Benito Matemáticas Aplicadas CS I 8

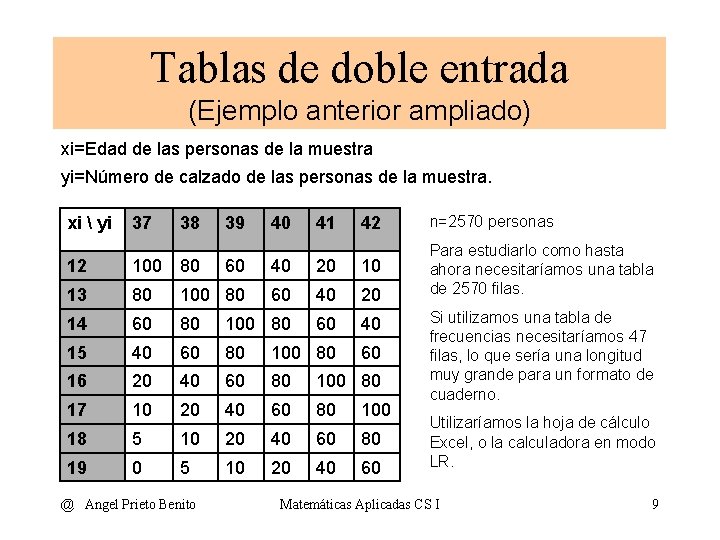
Tablas de doble entrada (Ejemplo anterior ampliado) xi=Edad de las personas de la muestra yi=Número de calzado de las personas de la muestra. xi yi 37 38 12 100 80 13 39 40 41 42 n=2570 personas Para estudiarlo como hasta ahora necesitaríamos una tabla de 2570 filas. 60 40 20 10 80 100 80 60 40 20 14 60 80 100 80 60 40 15 40 60 80 100 80 60 16 20 40 60 80 100 80 17 10 20 40 60 80 100 18 5 10 20 40 60 80 19 0 5 10 20 40 60 @ Angel Prieto Benito Si utilizamos una tabla de frecuencias necesitaríamos 47 filas, lo que sería una longitud muy grande para un formato de cuaderno. Utilizaríamos la hoja de cálculo Excel, o la calculadora en modo LR. Matemáticas Aplicadas CS I 9

• Hoja de cálculo Excel. • • La utilizaríamos para una tabla de frecuencias de 48 filas o registros. Tiene la ventaja de tener todo a la vista, pudiendo corregir fácilmente los errores de entrada de datos cometidos. Nos proporciona además el trazado gráfico de la recta de regresión, aunque sólo el de Y sobre X. Calculadora científica en modo LR. • • Volcamos los datos de la tabla a la calculadora directamente. Tiene la ventaja de no tener que teclear o buscar fórmulas como hay que hacer en la hoja de cálculo. Presenta la desventaja de tener que ser muy cuidadosos al meter los datos, al no tenerlos a la vista, aunque se pueden comprobar alguno de ellos sobre la marcha. No nos proporciona el trazado gráfico de la recta de regresión, salvo que sea además una calculadora gráfica. @ Angel Prieto Benito Matemáticas Aplicadas CS I 10