Distribucin NORMAL Es la distribucin ms importante en

Distribución NORMAL Es la distribución más importante en probabilidad y estadística. Muchas poblaciones tienen distribución normal o pueden ajustarse muy bien a ella. Ejemplos: • Estatura, peso y otras características físicas. • Errores de medición en experimentos científicos • Tiempos de reacción en experimentos psicológicos • Mediciones de inteligencia y aptitud. • Calificaciones en diversas pruebas. • Muchas medidas e indicadores económicos. 1 En 1835, Poisson acuñó la frase “ley de los grandes números” y demostró que había estabilidad estadística en cuestiones sociales.

Distribución NORMAL l 2 Se dice que una va X continua tiene una distribución normal con parámetros m y s (ó m y s 2) si su fdp es:

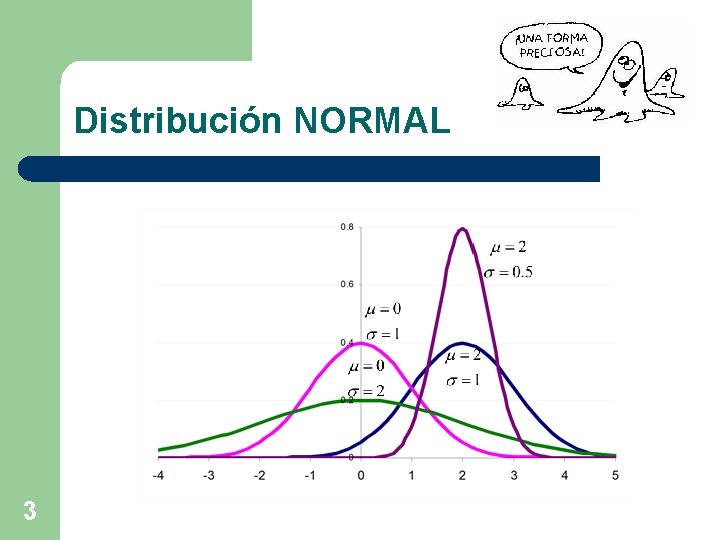
Distribución NORMAL 3

Distribución NORMAL l 4 Probabilidad de que una variable aleatoria normal se encuentre a y b:

Distribución NORMAL ESTÁNDAR l l l 5 La distribución normal con parámetros m = 0 y s = 1 recibe el nombre de distribución normal estándar. La variable aleatoria normal estándar se denota por Z y su fdp es: Su función de probabilidad acumulada se denota por:

Distribución NORMAL ESTÁNDAR Uso de tablas Si Z es una variable aleatoria Normal Estándar, determine: a) b) c) d) P(Z < 1. 5) el valor de z tal que P(Z > z) = 0. 975 P(-2. 33 < Z < 2. 33) el valor de w tal que la variable Z lo excede sólo con probabilidad 0. 001 e) el valor de z tal que P(-z < Z < z) = 0. 5 f) el percentil 95 de la distribución normal estándar. 6 a) 0. 9332; b) -1. 96; c) 0. 98; d) 3. 09; e) z = 0. 67; f) 1. 64.

Distribución NORMAL Si X tiene distribución normal con parámetros m y s, entonces: N (0, 1) Así, cualquier probabilidad que esté en términos de X se puede “estandarizar” poniéndola en términos de Z. 7

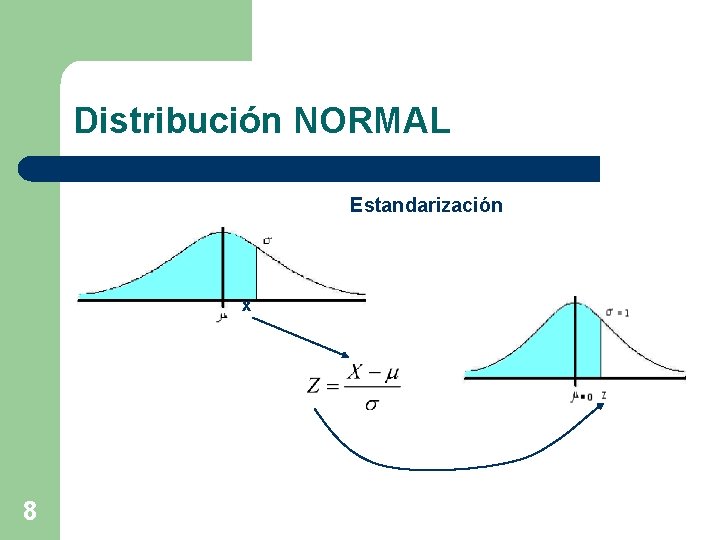
Distribución NORMAL Estandarización x 8

Distribución NORMAL Ejercicio: El tiempo que tarda un automovilista en reaccionar a las luces de freno traseras de otro vehículo que frena es crítico para ayudar a evitar una colisión. El artículo “Fast-Rice Brake Lamp as a Collision-Prevention Device” sugiere que el tiempo de reacción para una respuesta en tránsito, a una señal de frenado de luces de freno estándar se puede modelar con una distribución normal que tenga un valor medio de 1. 25 seg. y una desviación estándar de 0. 46 seg. ¿Cuál es la probabilidad de que el tiempo de reacción se encuentre 1. 00 y 1. 75 seg. ? 9 R: 0. 5653

Distribución NORMAL Ejercicio: Los resultados de la prueba de inteligencia Stanford-Binet IQ tiene distribución normal con media 100 y desviación estándar de 16. ¿Cuál es la probabilidad de que una persona seleccionada al azar obtenga una calificación… a) Mayor a 138? b) A menos de 2 desviaciones de la media? c) Hallar el percentil 90. 10 R: 0. 008704, 0. 9545, 120. 5

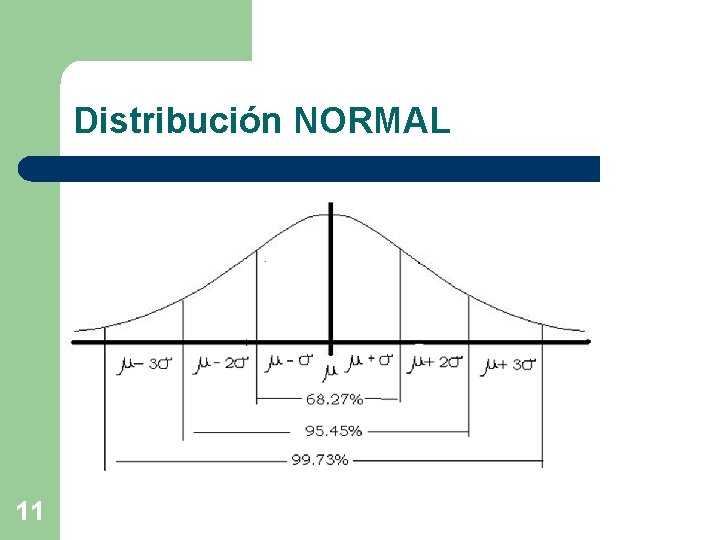
Distribución NORMAL 11

Distribución NORMAL l 12 Un producto de consumo diario en el hogar se envasa en paquetes cuyo contenido neto al llegar al consumidor es una variable aleatoria con distribución normal de media 12. 5 gr y desviación estándar de 2 gr. ¿Qué proporción de paquetes llegan al consumidor con menos de 8. 54 gr? R = 0. 0239

Distribución NORMAL Ejercicio Según el número de noviembre de 1993 de la revista Harper’s, los niños estadounidenses pasan entre 1200 y 1800 horas al año viendo televisión. Suponga que el tiempo que los niños pasan frente al televisor se distribuye normalmente con una media igual a 1500 horas y una desviación estándar de 100 horas. a. ¿Qué porcentaje vio televisión entre 1400 y 1600 horas? b. ¿Qué porcentaje vio televisión entre 1200 y 1800 horas? 13 R: 0. 6826, 0. 9973

Distribución NORMAL La calificación en una práctica de laboratorio es una variable aleatoria normalmente distribuida, con media de 6. 7 y desviación estándar de 1. 37. ¿Cuál es la calificación mínima aprobatoria si el 30. 5% reprueba la práctica? R = 6. 0013 14

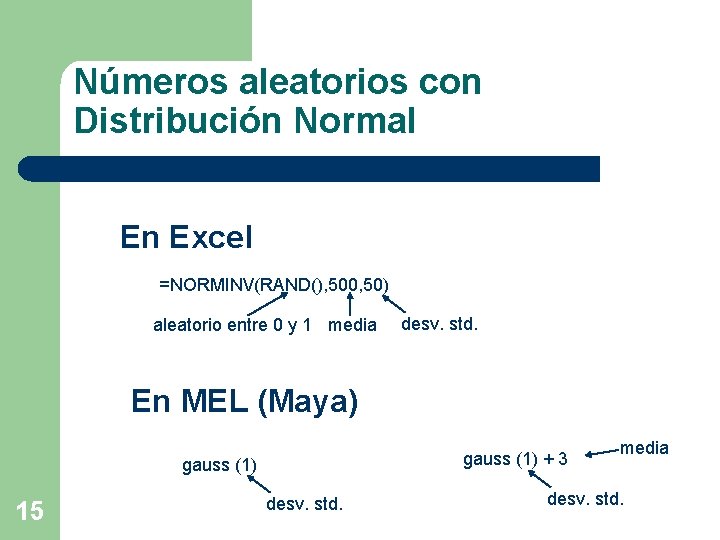
Números aleatorios con Distribución Normal En Excel =NORMINV(RAND(), 500, 50) aleatorio entre 0 y 1 media desv. std. En MEL (Maya) gauss (1) + 3 gauss (1) 15 desv. std. media desv. std.

Aleatorios 2. mel 16

Aleatorios 2. mel 17