Distribucin muestral de la Media RECUERDA Un elemento

Distribución muestral de la Media RECUERDA Un elemento muestral o punto de muestreo es cada uno de los posibles resultados de un evento. El conjunto de elementos muestrales o puntos de muestreo constituye el espacio muestral o universo de resultados posibles de un evento.

Distribución muestral de la Media «Teorema central del límite» Si de una población normal con media μx y una varianza , se extraen reiteradas muestras al azar, de tamaño N, la distribución de las medias de las muestras será normal con media μx y varianza.
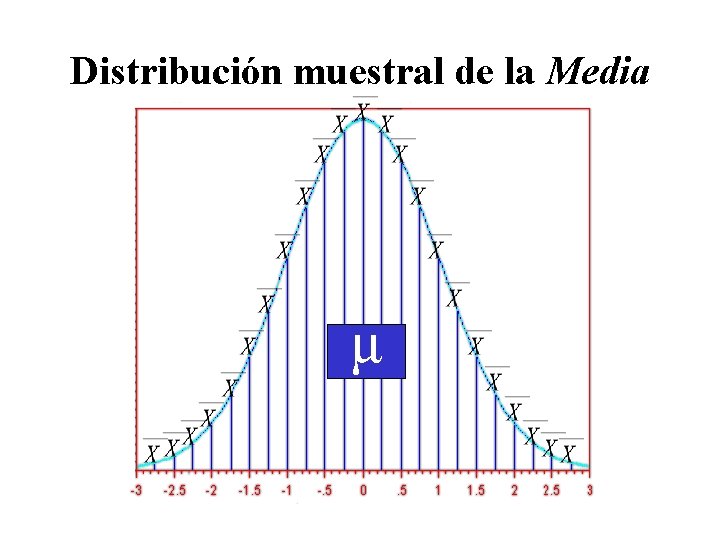
Distribución muestral de la Media μ

Distribución muestral de la Media «Ley de los grandes números» : Si se extraen diversas muestras del tamaño N al azar de una población cualquiera con media μx y una varianza , entonces, a medida que N crece, la distribución de muestreo de las medias de las muestras se aproxima a la normalidad con media μx y la varianza.
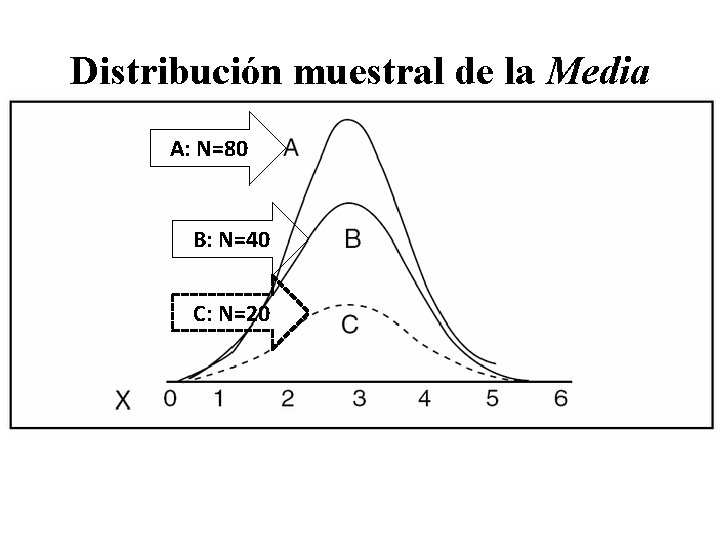
Distribución muestral de la Media A: N=80 B: N=40 C: N=20
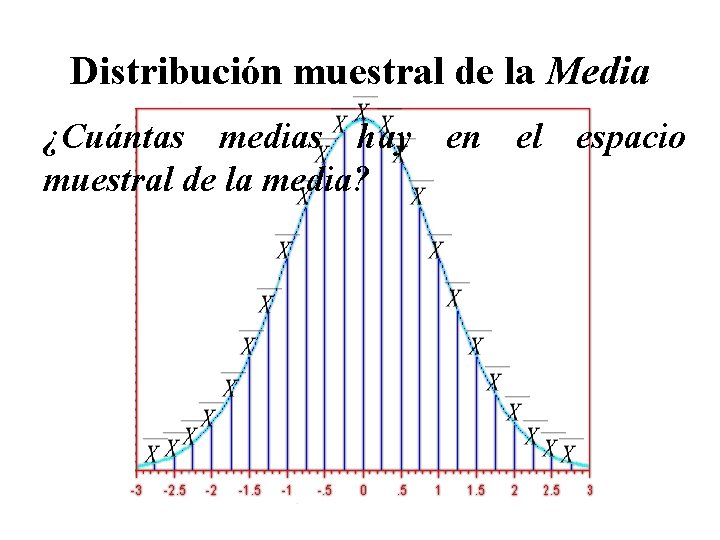
Distribución muestral de la Media ¿Cuántas medias hay en el espacio muestral de la media?

Distribución muestral de la Media La DISTRIBUCIÓN MUESTRAL de un estadístico es la distribución de frecuencias de los valores que estadístico toma en un número infinito de muestras del mismo tipo y tamaño, y la probabilidad de obtener cada valor, suponiendo que éste es producto del azar.

Distribución muestral de la Media La distribución muestral de la media proporciona todos los valores que puede asumir la media, junto con la probabilidad de obtener cada valor si el muestreo es aleatorio a partir de la población de la H 0.
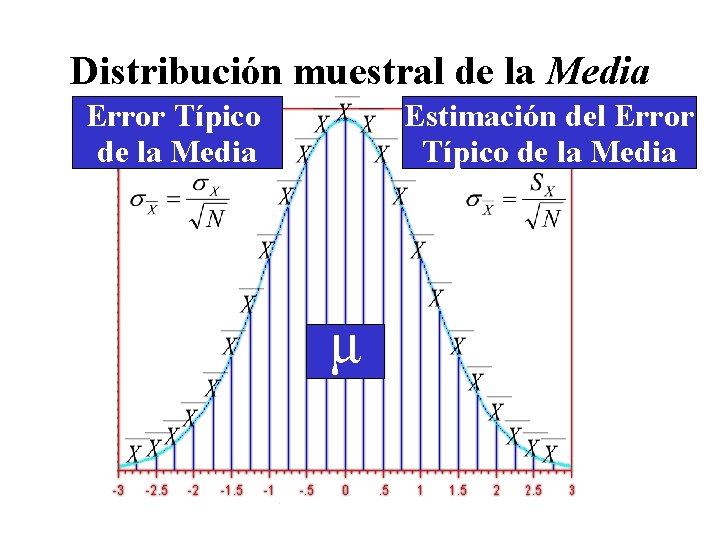
Distribución muestral de la Media Error Típico de la Media Estimación del Error Típico de la Media μ
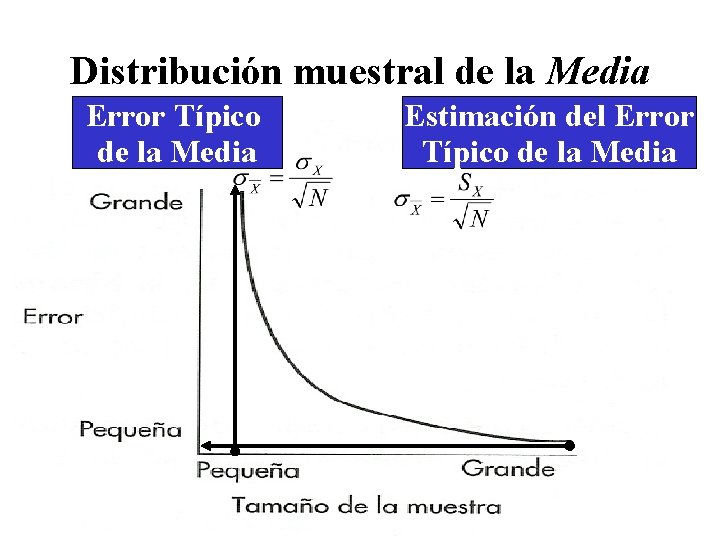
Distribución muestral de la Media Error Típico de la Media Estimación del Error Típico de la Media
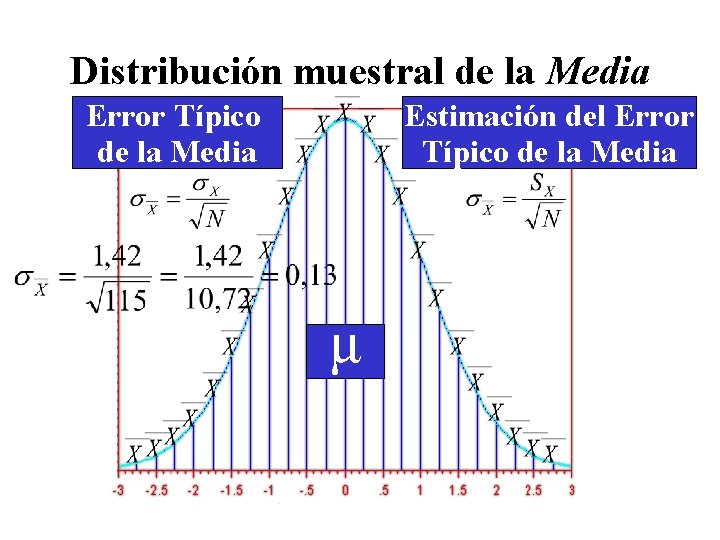
Distribución muestral de la Media Error Típico de la Media Estimación del Error Típico de la Media μ
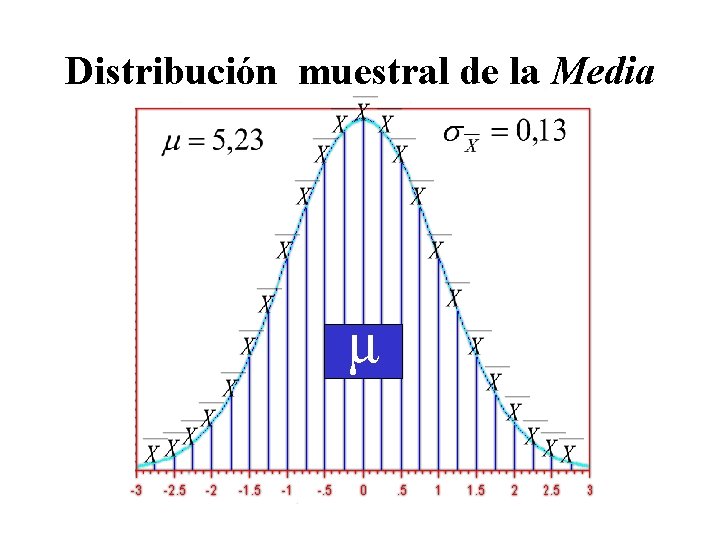
Distribución muestral de la Media μ
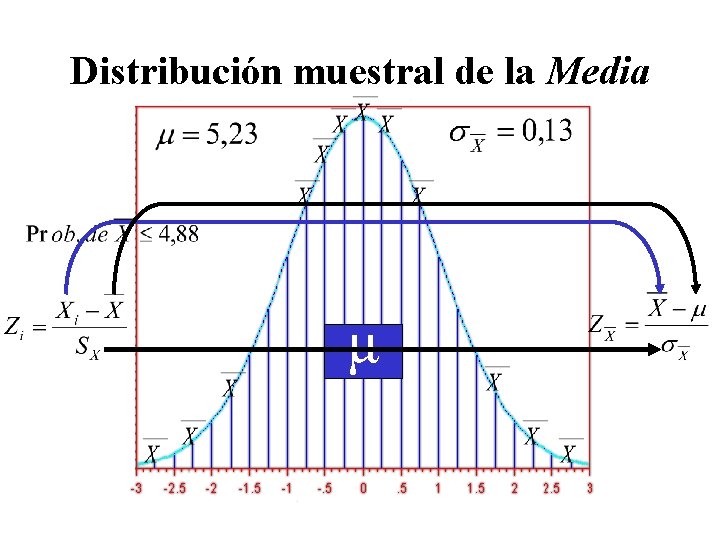
Distribución muestral de la Media μ
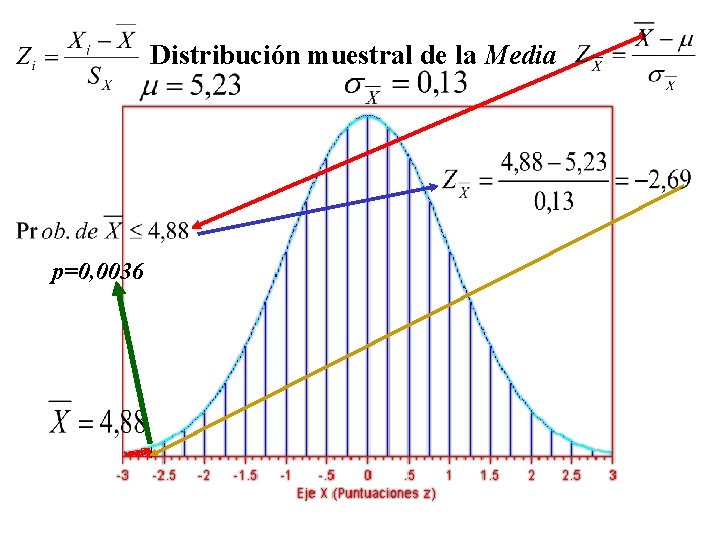
Distribución muestral de la Media p=0, 0036
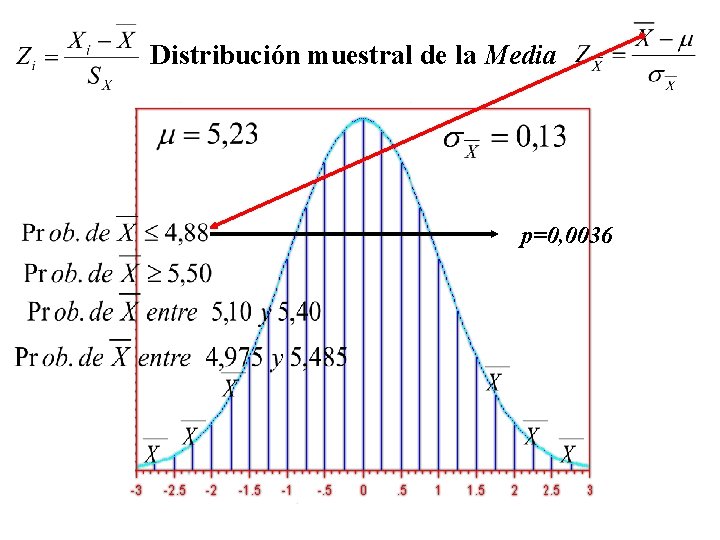
Distribución muestral de la Media p=0, 0036

INTERVALO CONFIDENCIAL μ desconocido μ estimado a través de la Media Muestral

INTERVALO CONFIDENCIAL Estimación puntual Estimación por intervalo Intervalo Confidencial Límites Confidenciales En general, el Intervalo Confidencial viene dado por las puntuaciones directas (medias muestrales) entre las cuales afirmamos, a un nivel de confianza dado (nc), nc que se encuentra el parámetro (μ) que consideramos. Nivel de Confianza p=0, 95 Margen de error p= =0, 05
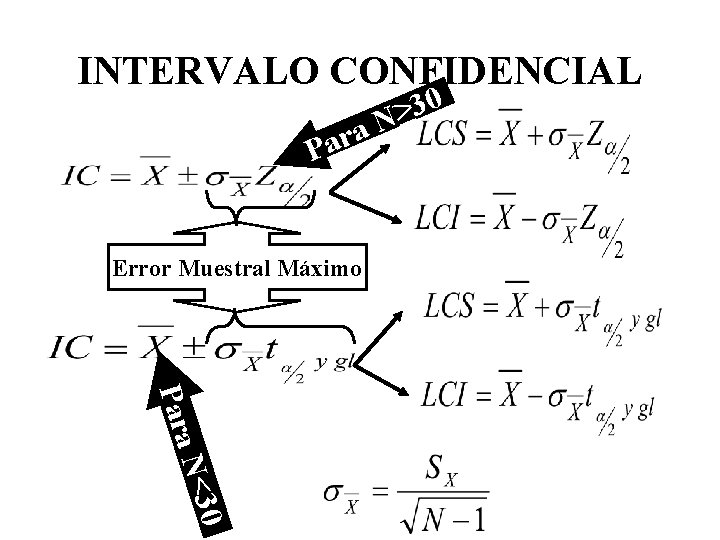
INTERVALO CONFIDENCIAL a r a P Error Muestral Máximo 0 3 ≥ N Para 0 N<3
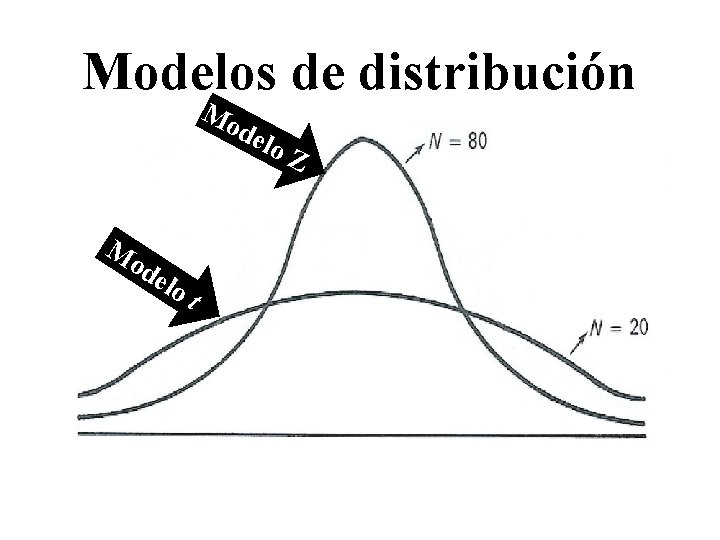
Modelos de distribución Mo del M od elo t o. Z
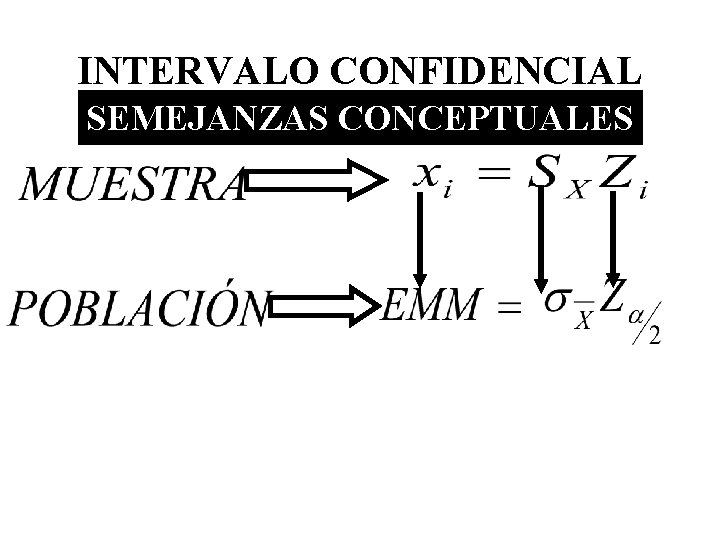
INTERVALO CONFIDENCIAL SEMEJANZAS CONCEPTUALES
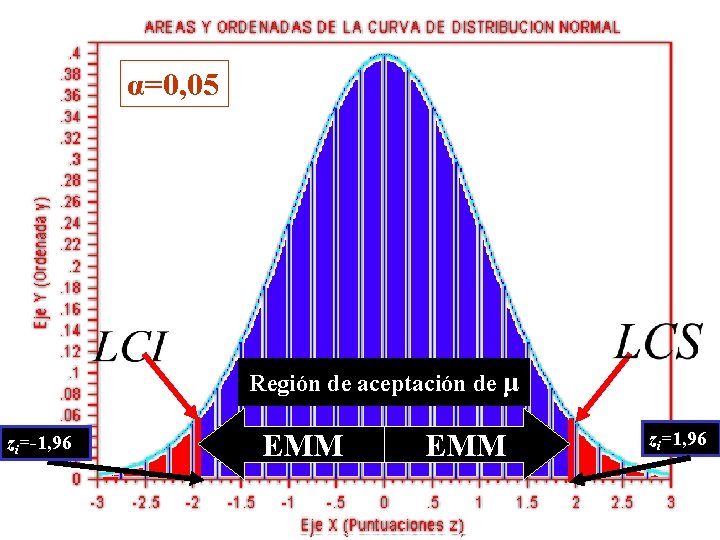
Distribución muestral de la Media α=0, 05 Región de aceptación de μ zi=-1, 96 EMM zi=1, 96

INTERVALO CONFIDENCIAL
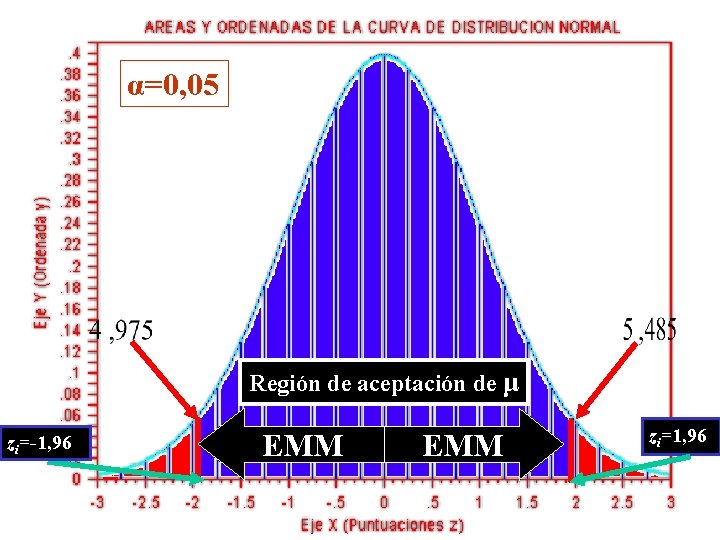
α=0, 05 Región de aceptación de μ zi=-1, 96 EMM zi=1, 96

INTERVALO CONFIDENCIAL

HIPÓTESIS • Se considera como HIPÓTESIS NULA (H 0) el POSTULADO DE NO DIFERENCIA entre los resultados obtenidos en la práctica y los teóricos. • Se considera como HIPÓTESIS ALTERNA(TIVA) (H 1) el POSTULADO DE DIFERENCIA entre los resultados obtenidos en la práctica y los teóricos.

HIPÓTESIS • HIPÓTESIS ALTERNA(TIVA) (H 1): 1) Bilateral, bidireccional, de dos colas 2) Unilateral, (uni)direccional, de una cola (1) HIPÓTESIS ALTERNA(TIVA) BILATERAL O BIDIRECCIONAL (H 1): El investigador afirma que las diferencias se pueden encontrar en cualquiera de los dos lados de la distribución muestral, a un nivel de confianza dado.
HIPÓTESIS
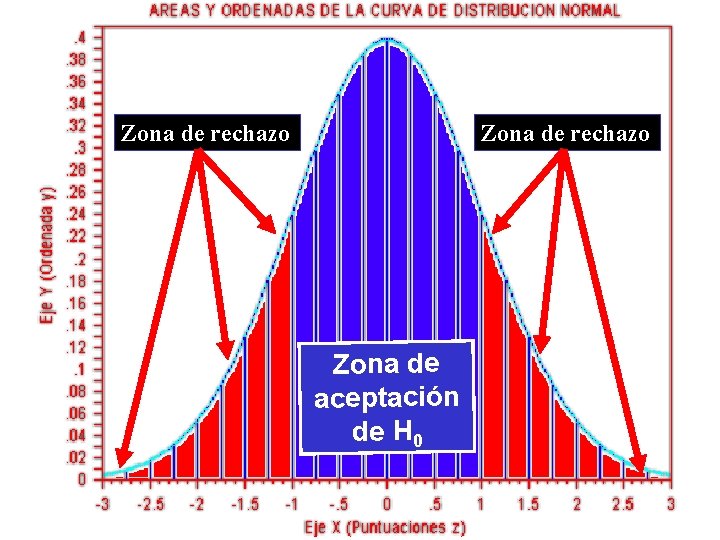
Zona de rechazo Zona de aceptación de H 0
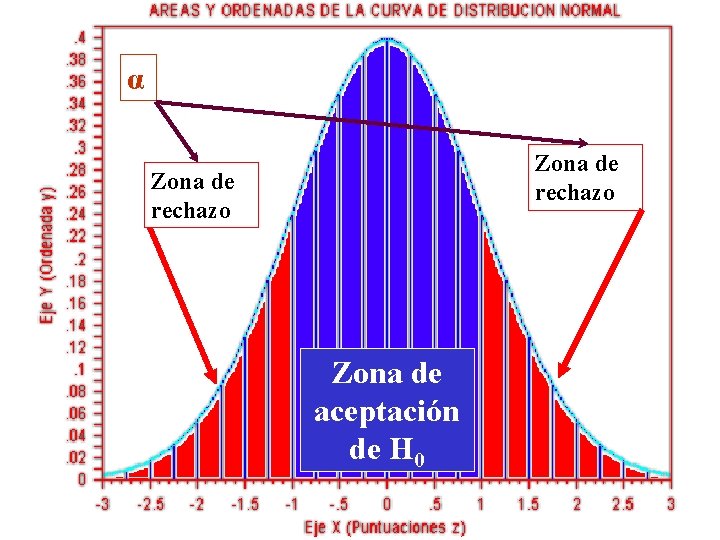
α Zona de rechazo Zona de aceptación de H 0
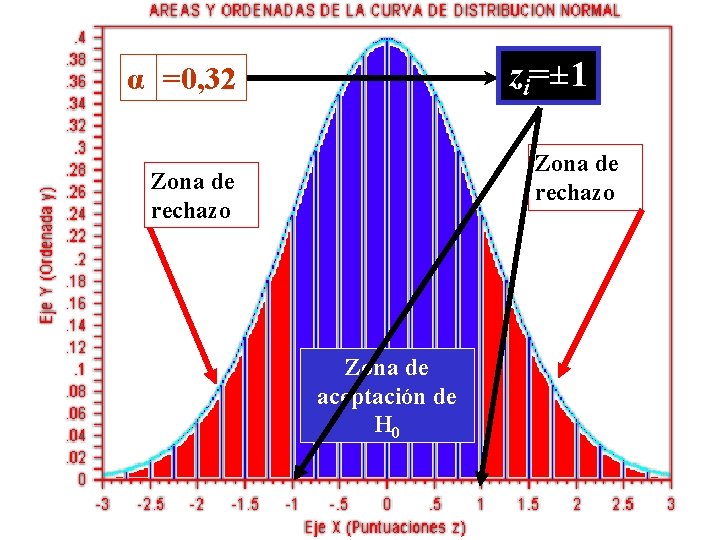
zi=± 1 α =0, 32 Zona de rechazo Zona de aceptación de H 0
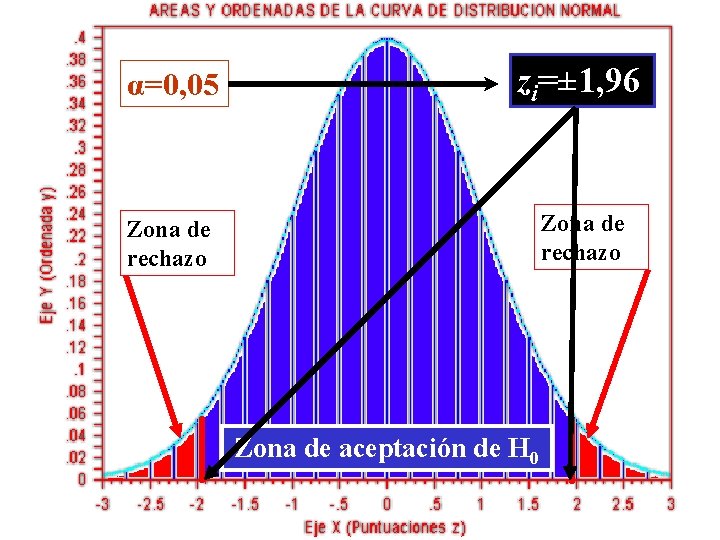
α=0, 05 zi=± 1, 96 Zona de rechazo Zona de aceptación de H 0
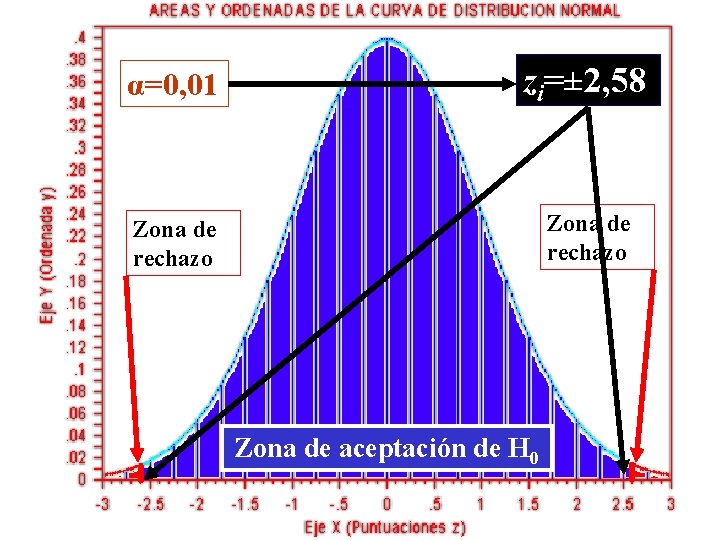
α=0, 01 zi=± 2, 58 Zona de rechazo Zona de aceptación de H 0

HIPÓTESIS (2) HIPÓTESIS ALTERNA(TIVA) UNILATERAL O DIRECCIONAL (H 1) : • El investigador afirma que las diferencias se encuentran en un determinado lado de la distribución muestral, a un nivel de confianza dado.
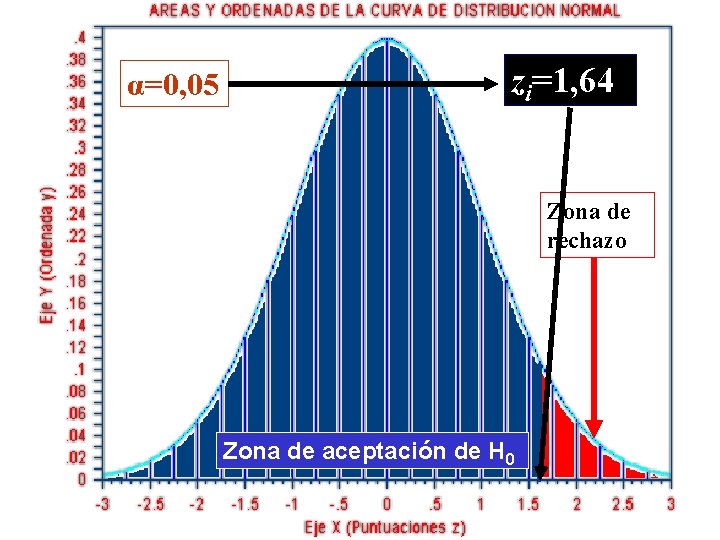
α=0, 05 zi=1, 64 Zona de rechazo Zona de aceptación de H 0

HIPÓTESIS Hipótesis sustantiva: El nivel de competencia percibida de la población de alumnos de 1º Grado es de unos 5, 50 puntos en una escala de 0 a 10. Se pretende probar la HIPÓTESIS de que la media poblacional (μ) en Competencia percibida hacia la estadística es igual a 5, 50 puntos, siendo el nivel de confianza del 95% (α=0, 05)

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 1) Formulación de la(s) H 0 y de su(s) correspondiente(s) H 1 2) Elección (justificada) de la Prueba Estadística 3) Especificación del Nivel de Error (α) 4) Definición de la Distribución Muestral 5) Zona de Rechazo/Aceptación de la(s) H 0 6) Cálculo del (los) estadístico(s): Prueba Estadística 7) Interpretación ESTADÍSTICA y PEDAGÓGICA

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 1. Formulación de la H 0 y de su correspondiente H 1 Hipótesis nula H 0: μ = 5, 50 La media poblacional de Competencia percibida es estadísticamente igual a 5, 50 Hipótesis alternativa H 1: μ ≠ 5, 50 La media poblacional de Competencia percibida no es estadísticamente igual a 5, 50

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 2. Elección de la Prueba Estadística Datos medidos a nivel de intervalo y N≥ 30, por tanto prueba estadística: Modelo zi o R. C. (Razón Crítica) para una muestra grande.

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 3. Especificación del Nivel de Error (α) Nivel de error (o de significación): En el problema se indica: α=0, 05.

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 4. Definición de la Distribución Muestral La distribución muestral es una distribución de probabilidad, que se forma con infinitas medias aritméticas obtenidas en infinitas muestras aleatorias de la misma población, todas del mismo tamaño que la del problema de investigación.

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 5. Zona de Rechazo/aceptación de H 0 La zona de rechazo de H 0 es una parte de la distribución muestral que está formada por todos los valores cuya probabilidad, si H 0 es verdadera, sea ≤ 0, 05. Puesto que H 1 no indica la dirección de las diferencias, la zona de rechazo está situada en ambos extremos de la distribución que incluye todos los valores cuya probabilidad sea ≤ 0, 05.

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 6. Cálculo del (los) estadístico(s): Prueba Estadística
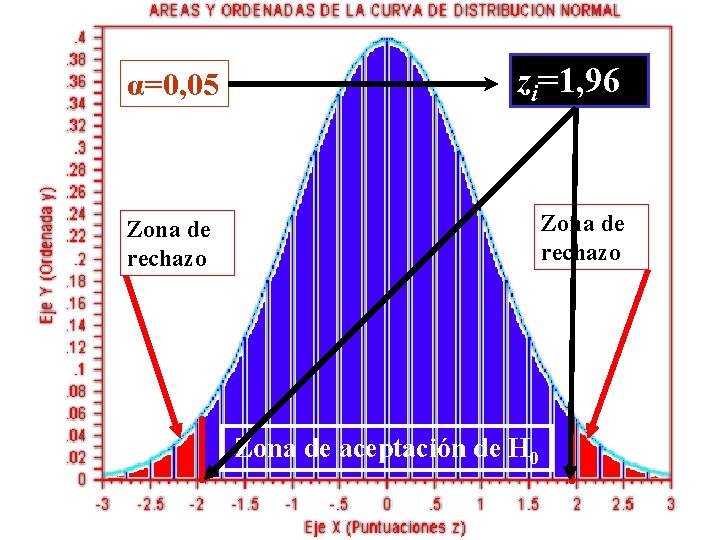
α=0, 05 zi=1, 96 Zona de rechazo Zona de aceptación de H 0
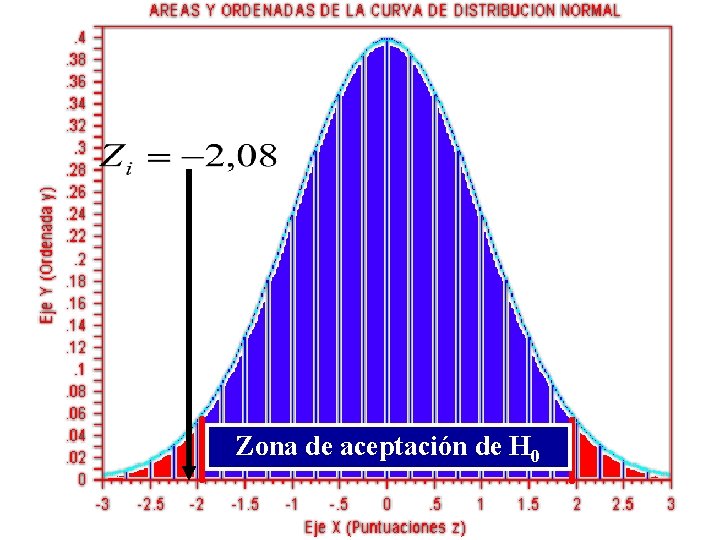
Zona de aceptación de H 0

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 7. Interpretación ESTADÍSTICA y PEDAGÓGICA Interpretación ESTADÍSTICA La probabilidad de obtener POR AZAR una zi = -2, 08 es menor que la de una zi =-1, 96 (α=0, 05); por tanto se rechaza H 0. Al tomar esta decisión se corre el riesgo de cometer Error del Tipo I.
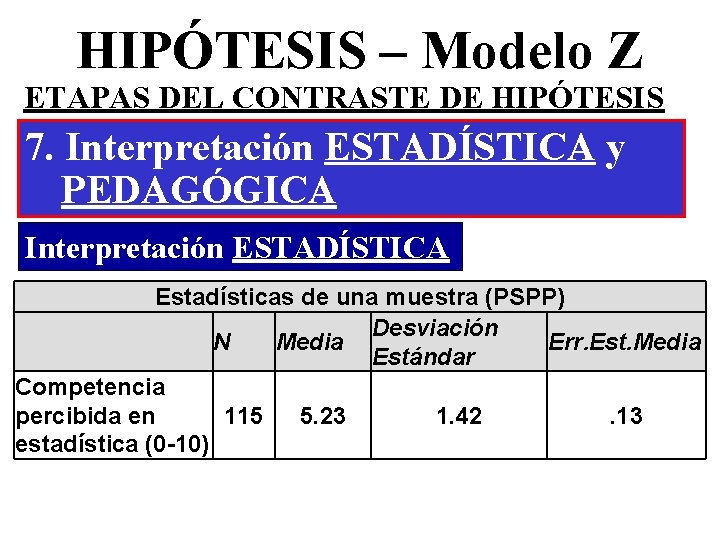
HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 7. Interpretación ESTADÍSTICA y PEDAGÓGICA Interpretación ESTADÍSTICA Estadísticas de una muestra (PSPP) Desviación N Media Err. Est. Media Estándar Competencia percibida en 115 5. 23 1. 42. 13 estadística (0 -10)

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 7. Interpretación ESTADÍSTICA y PEDAGÓGICA Interpretación ESTADÍSTICA Prueba de una muestra (PSPP) Valor de prueba = 5. 500000 Diferencia t df Sign. (2 -colas) Media Competencia -2. 06 114 percibida en estadística (0 -10) . 042 -. 27

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 7. Interpretación ESTADÍSTICA y PEDAGÓGICA Interpretación ESTADÍSTICA La probabilidad de obtener POR AZAR una tempírica=-2, 06 es de 0, 042, que es menor que (α) 0, 05; por tanto se rechaza H 0. Al tomar esta decisión se corre el riesgo de cometer el Error del Tipo I.

HIPÓTESIS – Modelo Z ETAPAS DEL CONTRASTE DE HIPÓTESIS 7. Interpretación ESTADÍSTICA y PEDAGÓGICA Interpretación PEDAGÓGICA Esto significa que la media poblacional (μ) de Competencia percibida hacia la estadística no es igual a 5, 50 puntos. La muestra no pertenece a esta población. ¿Podríamos estar equivocados con esta interpretación?
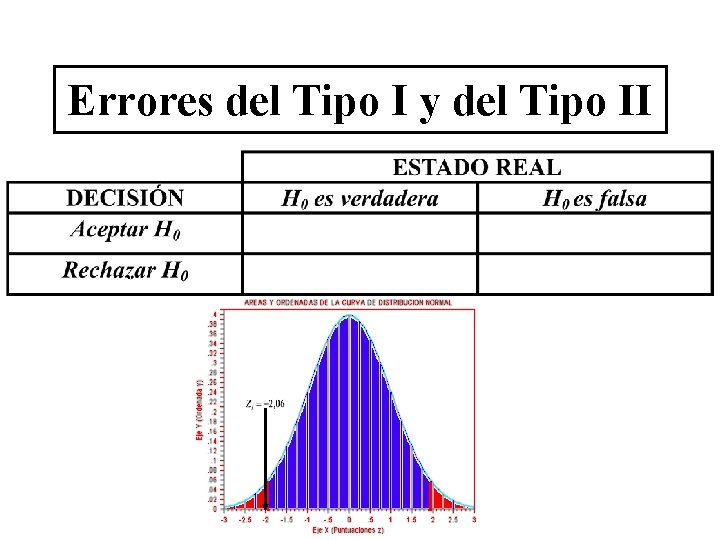
Errores del Tipo I y del Tipo II
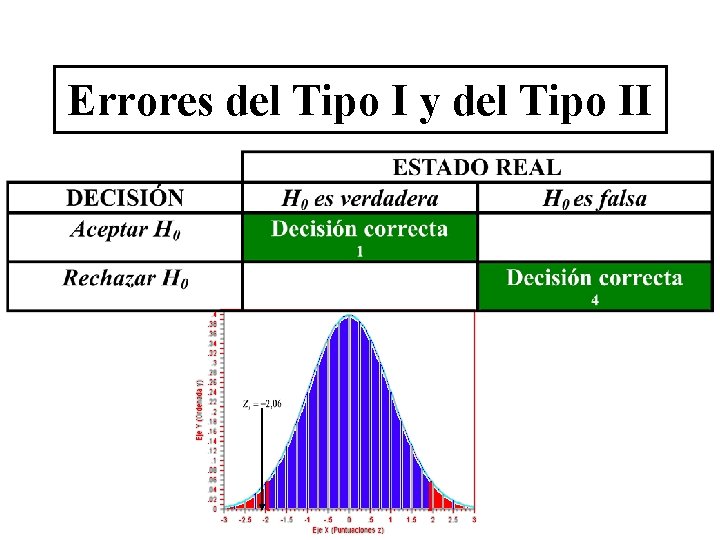
Errores del Tipo I y del Tipo II
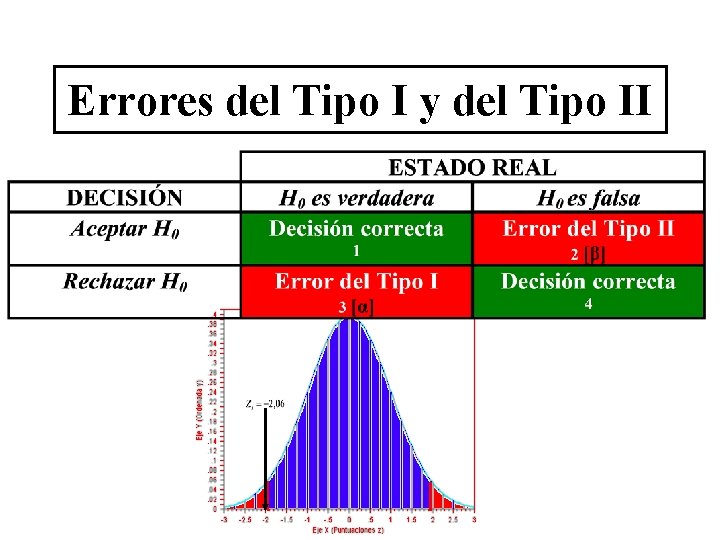
Errores del Tipo I y del Tipo II
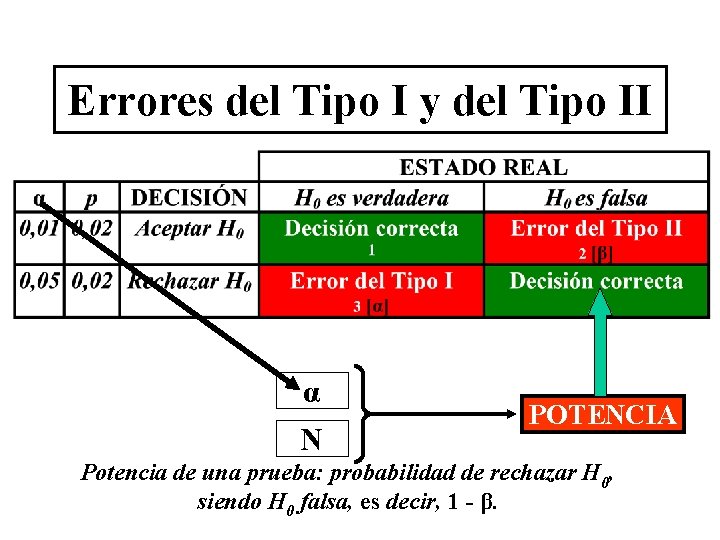
Errores del Tipo I y del Tipo II α N POTENCIA Potencia de una prueba: probabilidad de rechazar H 0, siendo H 0 falsa, es decir, 1 - β.
- Slides: 53