Distance measures Digital Image Processing M e a

M e a s u r e s • a. Various functions are used

d i s t a n c e De(p, q) = [(x-s)2 + (y-t)2]1/2

City Block (Manhattan) Distance • D 4(p, q) = |x-s| + |y-t| In this

Chess Board Distance: D 8(p, q) = max(|x-s|, |y-t|) • In this case, the

t i o n � • In the following arrangement of pixels, what’s the

i o n • In the following arrangement of pixels, what’s the value 6

Dm • Note that the D 4 and D 8 distances between p and

Example • Consider the following arrangement of pixels. p 3 p 4 p 1

Example • Now consider p 1 = 1 and p 3 = 0. 0

Example Calculate De, D 4 and D 8 distance between p and q in

Example Consider the image segment shown. (a) Let V={0, 1} and compute the lengths

Solution (a) V = {0, 1} 4 -path does not exist between p and

Solution (b) V = {1, 2} Shortest 4 -path length = 6 Shortest 8

Example Consider the image segments shown in figure. Compute the length of 4, 8

Solution (a) V = {1, 2} 4 2 3 3 2 3 (p)2 1

Solution (b) V = {2, 3} 4 2 3 3 2 3 (p)2 1

Exercise • Consider the image segment shown below in figure. • i) Let V

Slides: 20

Download presentation

Distance measures Digital Image. Processing

M e a s u r e s • a. Various functions are used to measure distance between two pixels Given 3 pixels p, q and z with coordinates (x, y), (s, t), (u, v) respectively, the distance function D has following properties: D(p, q) ≥ 0 [D(p, q) = 0, iff p = q] b. D(p, q) = D(q, p) c. D(p, z) ≤ D(p, q) + D(q, z) •

d i s t a n c e De(p, q) = [(x-s)2 + (y-t)2]1/2 • For this distance measure, the pixels having a distance less than or equal to some value r from (x, y) are the points contained in a disk of radius r centered at (x, y). r p

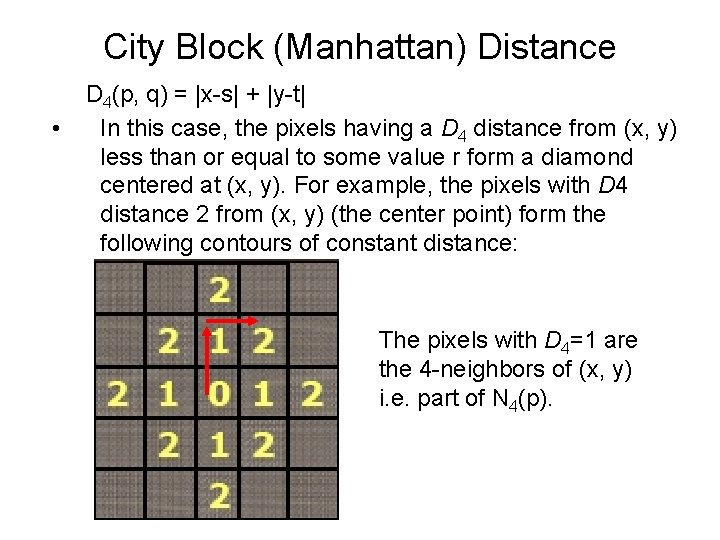
City Block (Manhattan) Distance • D 4(p, q) = |x-s| + |y-t| In this case, the pixels having a D 4 distance from (x, y) less than or equal to some value r form a diamond centered at (x, y). For example, the pixels with D 4 distance 2 from (x, y) (the center point) form the following contours of constant distance: The pixels with D 4=1 are the 4 -neighbors of (x, y) i. e. part of N 4(p).

Chess Board Distance: D 8(p, q) = max(|x-s|, |y-t|) • In this case, the pixels with. D 8 distance from (x, y) less than or equal to some valuer form a square centered at (x, y). For example, the pixels with D 8 distance 2 from (x, y) (the center point) form the following contours of constant distance: The pixels with D 8=1 are the 8 -neighbors of (x, y), i. e. part of N 8(x, y)

t i o n � • In the following arrangement of pixels, what’s the value of the chessboard distance between the circled two points? 0 0 0 0 1 1 0 0 0 0 0

t i o n � • In the following arrangement of pixels, what’s the value of the chessboard distance between the circled two points? 0 0 0 0 1 1 0 0 0 0 0 2

i o n • In the following arrangement of pixels, what’s the value 6 of the city-block distance between the circled two � points? 0 0 0 0 1 1 0 0 0 0 0

i o n • In the following arrangement of pixels, what’s the value 6 of the city-block distance between the circled two � points? 0 0 0 0 1 1 0 0 0 0 0 4

Dm • Note that the D 4 and D 8 distances between p and q are independent of any paths that might exist between the points because these distances involve only the coordinates of the end points. • If we elect to consider m-adjacency, however, the Dm distance between two points is defined as the shortest m-path between the points. In this case, the distance between two pixels will depend on the values of the pixels along the path, as well as the values of their neighbors.

Example • Consider the following arrangement of pixels. p 3 p 4 p 1 p 2 p • Let p= p 2 = p 4 =1 and that p 1 and p 3 can be 0 or 1. • First consider p 1 = p 3 = 0 and V = {1} 0 1 1 Dm (p, p 4) = 2

Example • Now consider p 1 = 1 and p 3 = 0. 0 1 1 p 2 and p are no longer be m-adjacent so, Dm (p, p 4) = 3 Path = p p 1 p 2 p 4. Now let p 1 = p 3 = 1. 1 1 1 p 2 and p 4 are no longer be m-adjacent so, Dm (p, p 4) = 4 Path = p p 1 p 2 p 3 p 4.

Example Calculate De, D 4 and D 8 distance between p and q in an image shown below. 0 1 1 1(q) 1 0 0 0 1 1 (p)1 1 0 1 1 (0, 3)1 1 0 1 0 1(3, 0) 0 1 1 De = √(9+9) = 4. 2 0 1 1 (0, 3)1 1 0 1 0 1(3, 0) 0 1 1 D 4 = 3 + 3 = 6 0 1 1 (0, 3)1 1 0 1 0 1(3, 0) 0 1 1 D 8 = max(3, 3) = 3

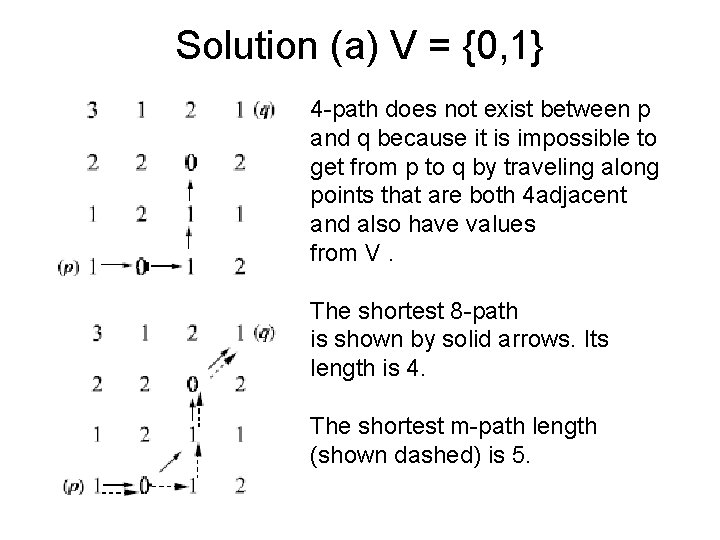
Example Consider the image segment shown. (a) Let V={0, 1} and compute the lengths of the shortest 4 -, 8 -, and m-path between p and q. If a particular path does not exist between these two points, explain why. (b) Repeat for V={1, 2}. 3 1 2 1(q) 2202 1211 (p) 1 0 1 2

Solution (a) V = {0, 1} 4 -path does not exist between p and q because it is impossible to get from p to q by traveling along points that are both 4 adjacent and also have values from V. The shortest 8 -path is shown by solid arrows. Its length is 4. The shortest m-path length (shown dashed) is 5.

Solution (b) V = {1, 2} Shortest 4 -path length = 6 Shortest 8 - path length = 4 Shown by solid arrows Shortest m-path length = 5 Shown by dashed arrows

Example Consider the image segments shown in figure. Compute the length of 4, 8 & m-path between 'p' and 'q' where V = {1, 2} & repeat for V = {2, 3} 4 2 1 2(q) 3313 2322 (p)2 1 2 3

Solution (a) V = {1, 2} 4 2 3 3 2 3 (p)2 1 1 1 2 2 2(q) 3 2 3 4 -path = 6 4 2 3 3 2 3 (p)2 1 1 1 2 2 2(q) 3 2 3 8 -path = 4 4 2 3 3 2 3 (p)2 1 1 1 2 2 2(q) 3 2 3 m-path = 6

Solution (b) V = {2, 3} 4 2 3 3 2 3 (p)2 1 1 1 2 2 2(q) 3 2 3 4 -path = 6 4 2 3 3 2 3 (p)2 1 1 1 2 2 2(q) 3 2 3 8 -path = 4 4 2 3 3 2 3 (p)2 1 1 1 2 2 2(q) 3 2 3 m-path = 6

Exercise • Consider the image segment shown below in figure. • i) Let V = {1, 2} and compute the length of shortest 4 -, 8 and m- path between P and Q. If a particular path does not exist. Explain why.