Distance Displacement Velocity and Acceleration RECAP b Distance

Distance, Displacement, Velocity and Acceleration

RECAP b Distance b Displacement b Velocity b Acceleration

Distance b Distance (d) – how far an object travels. • Does not depend on direction. b Imagine an ant crawling along a ruler. 0 cm 1 2 3 4 5 6 7 8 b What distance did the ant travel? • d = 3 cm 9 10

Distance b Distance does not depend on direction. b Here’s our intrepid ant explorer again. 0 cm 1 2 3 4 5 6 7 8 9 b Now what distance did the ant travel? • d = 3 cm b Does his direction change the answer? 10

Displacement b Displacement – difference between an object’s final position and its starting position. b Displacement = final position – initial position = dfinal – dinitial b In order to define displacement, we need directions. b Examples of directions: b • • • + and – N, S, E, W Angles

Displacement vs. Distance b Example of distance: • The ant walked 3 cm. b Example of displacement: • The ant walked 3 cm EAST. b An object’s distance traveled and its displacement aren’t always the same!

Example John walks from the point A to B to C. What does the distance he travel? What is the displacement? Let's calculate first the distance that john travels. While calculating distance, we look at the numeric value of interval between traveled points. As you can see from Figure he travels from A to B to C. Distance from A to B is 4 m and B to C is 3 m. Their sum will give us total distance; 4+3=7 Displacement vector is an between the final position and initial poistions. As it clearly seen in the Figure between A to C is 5 m. So, our displacement vector is 5 m and it's direction is from the point A to C.

Displacement vs. Distance b An athlete runs around a track that is 100 meters long three times, then stops. • What is the athlete’s distance and displacement? b Distance = 300 m b Displacement = 0 m b Why?

Speed b A force is a push or a pull b When a force acts on an object, one possible result is motion.

Speed b A reference point is generally a stationary object such as a tree, a street sign, or a line on the road. b Once a reference point has been established, it is possible to define the motion of an object in terms of speed, position, and direction.

Speed b The speed of an object refers to how fast an object moves. • To determine speed you need to know both the distance an object moves and the amount of time needed to travel.

Speed b Calculations using formulas b b Most objects do not move at a constant, unchanging speed. When you use the formula to find the speed of an object you’re actually finding the object’s average speed.

Speed b The diagram shows how two automobiles with different speeds move during the same amount of time.
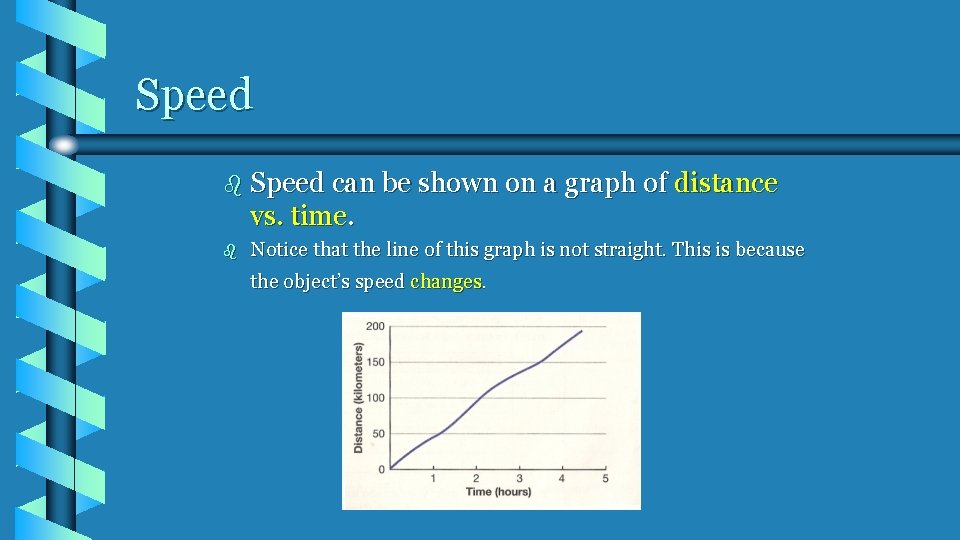
Speed b Speed can be shown on a graph of distance vs. time. b Notice that the line of this graph is not straight. This is because the object’s speed changes.

Velocity b Velocity is the speed of an object in a particular direction. b Suppose that two cars traveled at 50 kilometers per hour on the same highway for 2 hours. After two hours, the cars are 200 kilometers away from each other. How is this possible? b Answer: They were traveling in opposite directions.

Velocity b Speed describes distance and time, but does not indicate direction. b When the direction of an object’s movement is included, you are describing an object’s velocity.

Velocity b Velocity speed with direction • If a sailboat’s speed goes from 4 knots to 7 knots, its velocity has changed. If the sailboat continues moving at 7 knots, but changes direction, its velocity has again changed.

Acceleration b Acceleration is the rate at which an object’s velocity changes. • Velocity changes when an object’s speed and direction changes. • Acceleration of an object also changes if its speed or its direction changes. • Can be an: – Increase in speed – Decrease in speed – Change in direction

Acceleration b You can calculate the average acceleration of an object by using the following equation. ¡ Units of acceleration: l m/s 2

Acceleration b Acceleration is recorded in units such as meters per second squared (m/s 2). Acceleration of a car b Based on this data, you can see that the acceleration of the car at any time is 5 m/s/s or 5 m/s 2. Every second, the velocity of the car increases by 5 m/s.
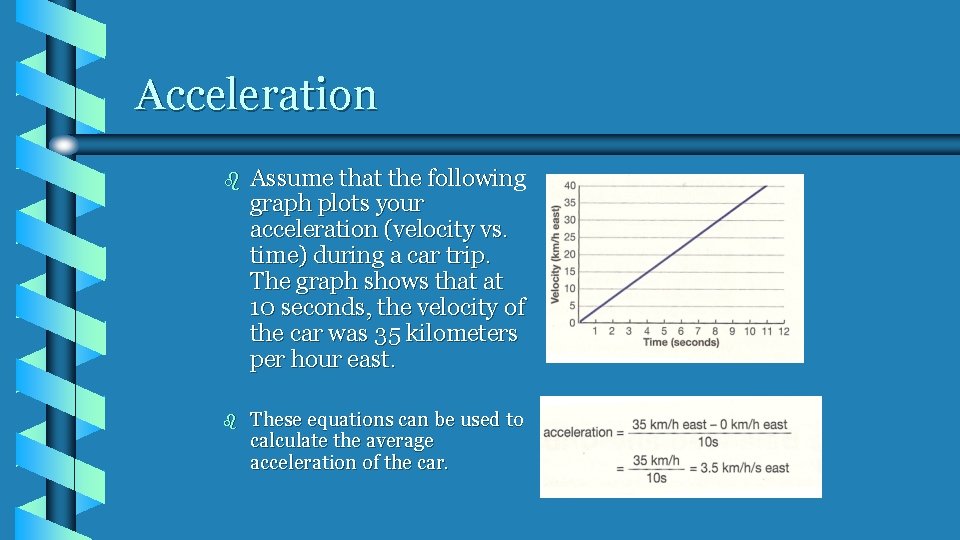
Acceleration b Assume that the following graph plots your acceleration (velocity vs. time) during a car trip. The graph shows that at 10 seconds, the velocity of the car was 35 kilometers per hour east. b These equations can be used to calculate the average acceleration of the car.

Graphing Acceleration b Can use 2 kinds of graphs • Speed vs. time • Distance vs. time
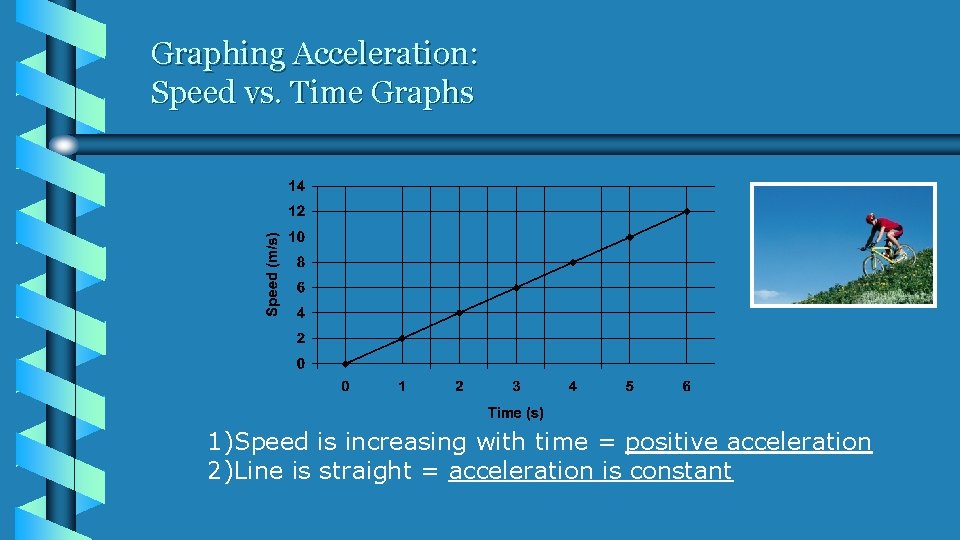
Graphing Acceleration: Speed vs. Time Graphs 1)Speed is increasing with time = positive acceleration 2)Line is straight = acceleration is constant
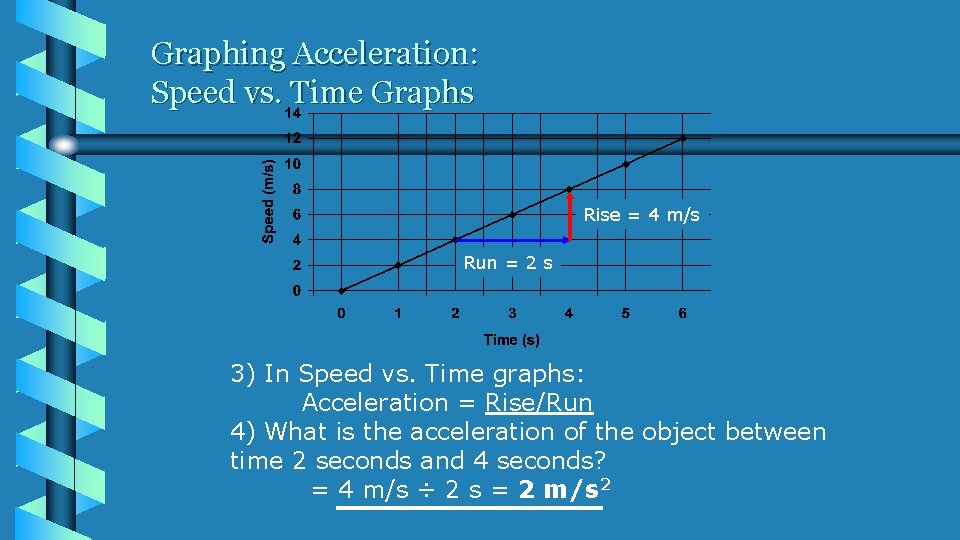
Graphing Acceleration: Speed vs. Time Graphs Rise = 4 m/s Run = 2 s 3) In Speed vs. Time graphs: Acceleration = Rise/Run 4) What is the acceleration of the object between time 2 seconds and 4 seconds? = 4 m/s ÷ 2 s = 2 m/s 2
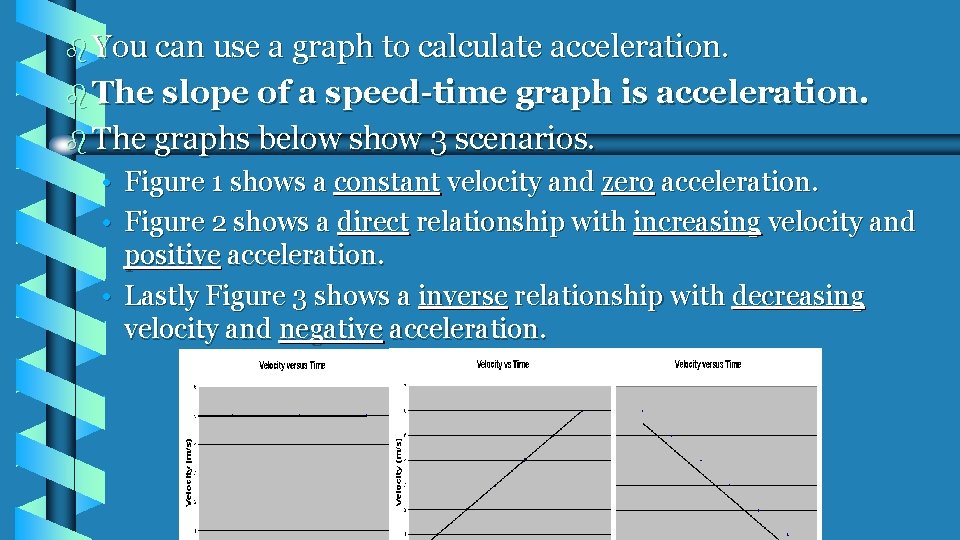
b You can use a graph to calculate acceleration. b The slope of a speed-time graph is acceleration. b The graphs below show 3 scenarios. • Figure 1 shows a constant velocity and zero acceleration. • Figure 2 shows a direct relationship with increasing velocity and positive acceleration. • Lastly Figure 3 shows a inverse relationship with decreasing velocity and negative acceleration.
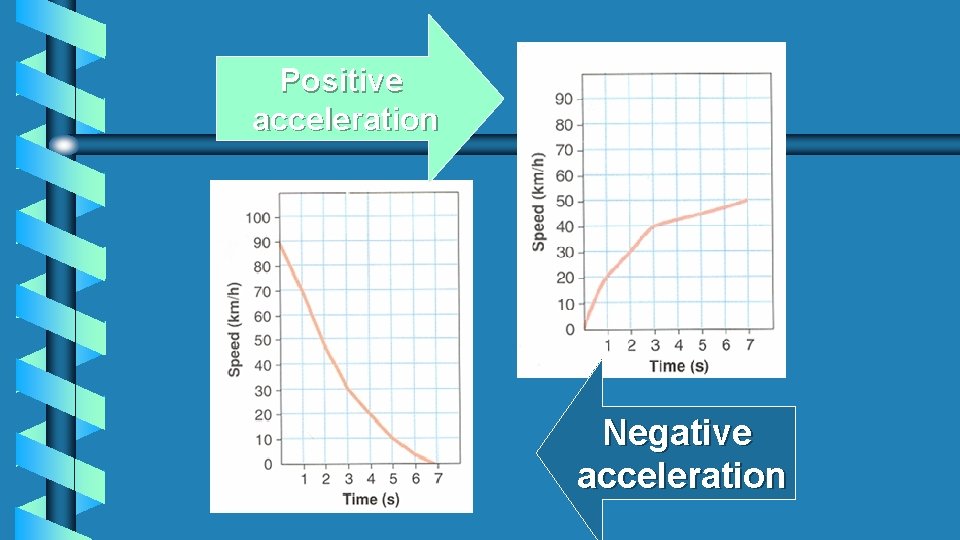
Positive acceleration Negative acceleration
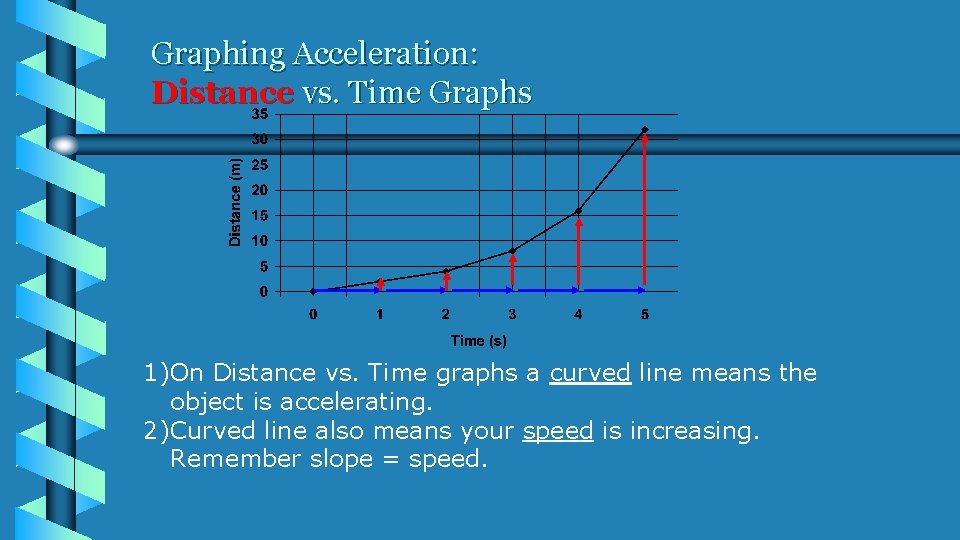
Graphing Acceleration: Distance vs. Time Graphs 1)On Distance vs. Time graphs a curved line means the object is accelerating. 2)Curved line also means your speed is increasing. Remember slope = speed.
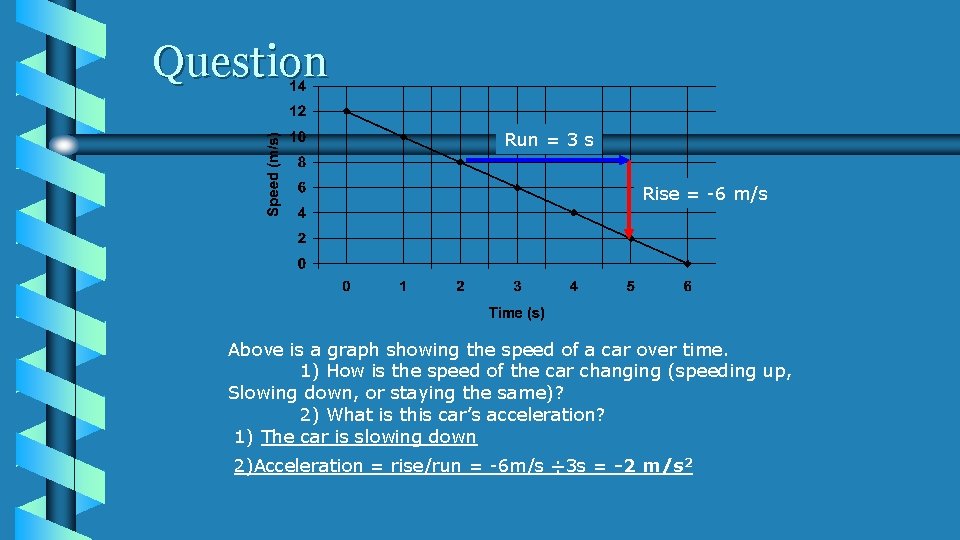
Question Run = 3 s Rise = -6 m/s Above is a graph showing the speed of a car over time. 1) How is the speed of the car changing (speeding up, Slowing down, or staying the same)? 2) What is this car’s acceleration? 1) The car is slowing down 2)Acceleration = rise/run = -6 m/s ÷ 3 s = -2 m/s 2
- Slides: 28