Dissociative Electron Attachment to H 2 O via

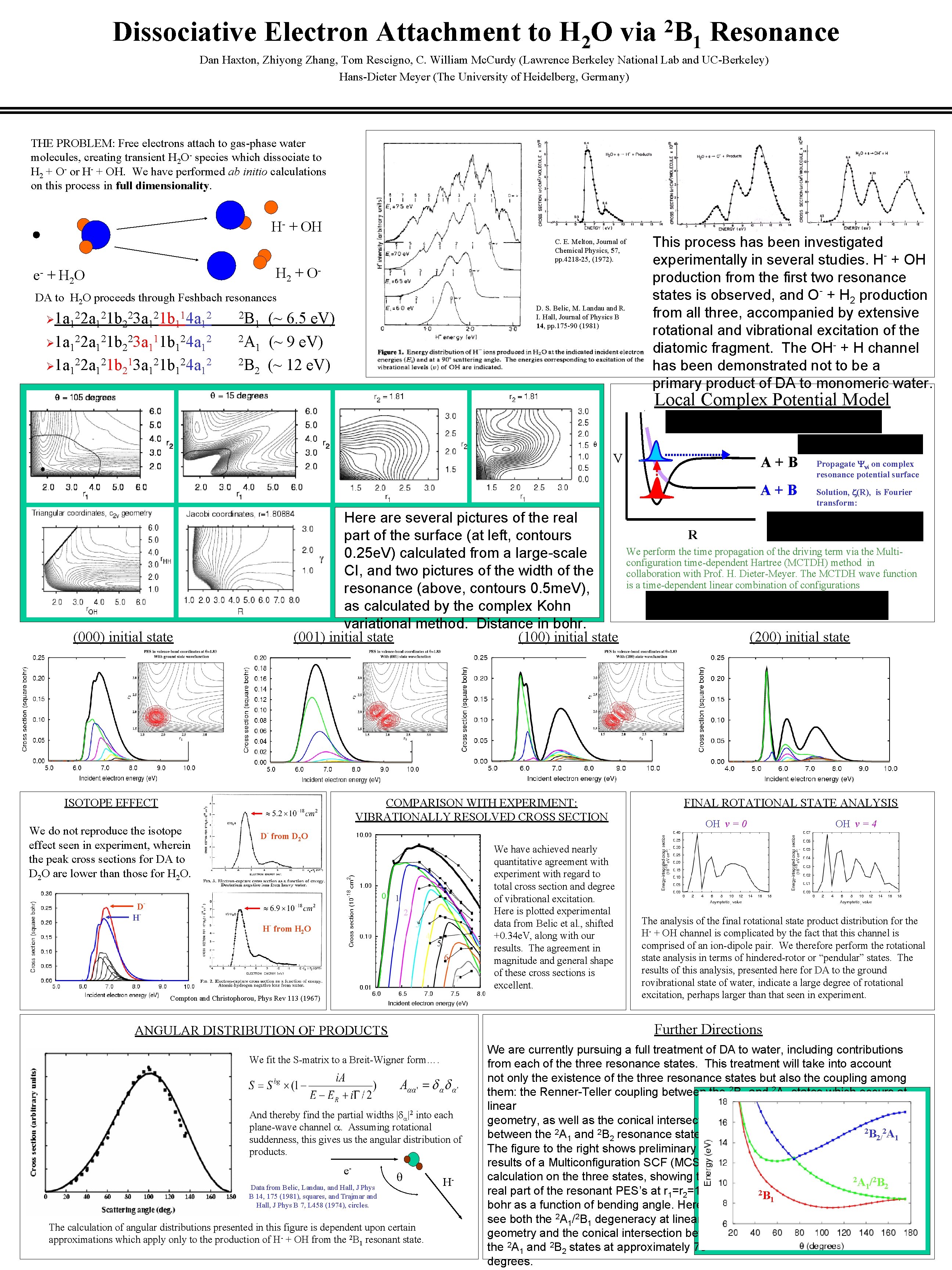
Dissociative Electron Attachment to H 2 O via 2 B Resonance 1 Dan Haxton, Zhiyong Zhang, Tom Rescigno, C. William Mc. Curdy (Lawrence Berkeley National Lab and UC-Berkeley) Hans-Dieter Meyer (The University of Heidelberg, Germany) THE PROBLEM: Free electrons attach to gas-phase water molecules, creating transient H 2 O- species which dissociate to H 2 + O- or H- + OH. We have performed ab initio calculations on this process in full dimensionality. H- + OH C. E. Melton, Journal of Chemical Physics, 57, pp. 4218 -25, (1972). e- H 2 + O - + H 2 O DA to H 2 O proceeds through Feshbach resonances 2 2 1 2 Ø 1 a 1 2 a 1 1 b 2 3 a 1 1 b 1 4 a 1 Ø 1 a 122 a 121 b 223 a 111 b 124 a 12 Ø 1 a 122 a 121 b 213 a 121 b 124 a 12 2 B D. S. Belic, M. Landau and R. I. Hall, Journal of Physics B 14, pp. 175 -90 (1981) (~ 6. 5 e. V) 2 A (~ 9 e. V) 1 2 B (~ 12 e. V) 2 1 This process has been investigated experimentally in several studies. H + OH production from the first two resonance states is observed, and O + H 2 production from all three, accompanied by extensive rotational and vibrational excitation of the diatomic fragment. The OH- + H channel has been demonstrated not to be a primary product of DA to monomeric water. Local Complex Potential Model V A+B - A+B Here are several pictures of the real part of the surface (at left, contours 0. 25 e. V) calculated from a large-scale CI, and two pictures of the width of the resonance (above, contours 0. 5 me. V), as calculated by the complex Kohn variational method. Distance in bohr. (001) initial state (100) initial state (000) initial state ISOTOPE EFFECT COMPARISON WITH EXPERIMENT: VIBRATIONALLY RESOLVED CROSS SECTION We do not reproduce the isotope effect seen in experiment, wherein the peak cross sections for DA to D 2 O are lower than those for H 2 O. D H- D- from D 2 O 0 - 1 2 3 - H from H 2 O 4 5 6 7 Compton and Christophorou, Phys Rev 113 (1967) We fit the S-matrix to a Breit-Wigner form…. And thereby find the partial widths | |2 into each plane-wave channel . Assuming rotational suddenness, this gives us the angular distribution of products. Data from Belic, Landau, and Hall, J Phys B 14, 175 (1981), squares, and Trajmar and Hall, J Phys B 7, L 458 (1974), circles. Solution, z(R), is Fourier transform: R We perform the time propagation of the driving term via the Multiconfiguration time-dependent Hartree (MCTDH) method in collaboration with Prof. H. Dieter-Meyer. The MCTDH wave function is a time-dependent linear combination of configurations (200) initial state FINAL ROTATIONAL STATE ANALYSIS OH v = 0 OH v = 4 The analysis of the final rotational state product distribution for the H- + OH channel is complicated by the fact that this channel is comprised of an ion-dipole pair. We therefore perform the rotational state analysis in terms of hindered-rotor or “pendular” states. The results of this analysis, presented here for DA to the ground rovibrational state of water, indicate a large degree of rotational excitation, perhaps larger than that seen in experiment. Further Directions ANGULAR DISTRIBUTION OF PRODUCTS e- We have achieved nearly quantitative agreement with experiment with regard to total cross section and degree of vibrational excitation. Here is plotted experimental data from Belic et al. , shifted +0. 34 e. V, along with our results. The agreement in magnitude and general shape of these cross sections is excellent. Propagate i on complex resonance potential surface The calculation of angular distributions presented in this figure is dependent upon certain approximations which apply only to the production of H- + OH from the 2 B 1 resonant state. H- We are currently pursuing a full treatment of DA to water, including contributions from each of the three resonance states. This treatment will take into account not only the existence of the three resonance states but also the coupling among them: the Renner-Teller coupling between the 2 B 1 and 2 A 1 states which occurs at linear geometry, as well as the conical intersection 2 B 2 A between the 2 A 1 and 2 B 2 resonance states. 2/ 1 The figure to the right shows preliminary results of a Multiconfiguration SCF (MCSCF) calculation on the three states, showing the 2 A /2 B 1 2 real part of the resonant PES’s at r 1=r 2=1. 81 2 B 1 bohr as a function of bending angle. Here you see both the 2 A 1/2 B 1 degeneracy at linear geometry and the conical intersection between the 2 A 1 and 2 B 2 states at approximately 75 degrees.