Disorder and chaos in quantum systems II Lecture

Disorder and chaos in quantum systems II. Lecture 2. Boris Altshuler Physics Department, Columbia University

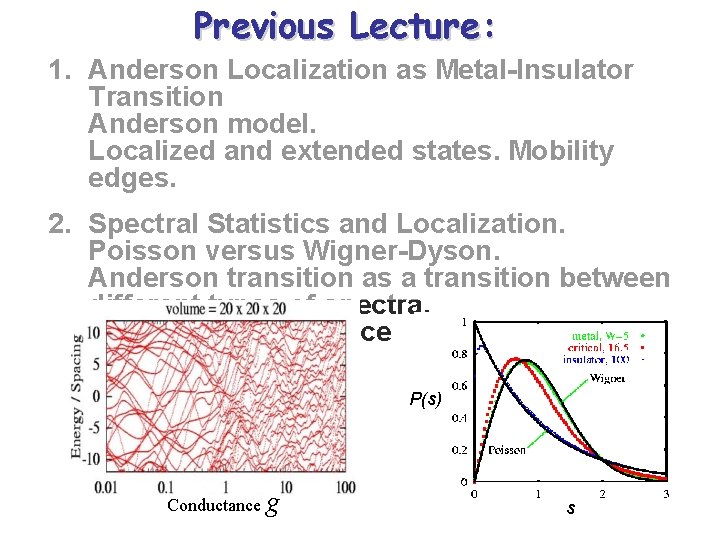
Previous Lecture: 1. Anderson Localization as Metal-Insulator Transition Anderson model. Localized and extended states. Mobility edges. 2. Spectral Statistics and Localization. Poisson versus Wigner-Dyson. Anderson transition as a transition between different types of spectra. Thouless conductance P(s) Conductance g s

Lecture 2. 1. Quantum Chaos, Integrability and Localization

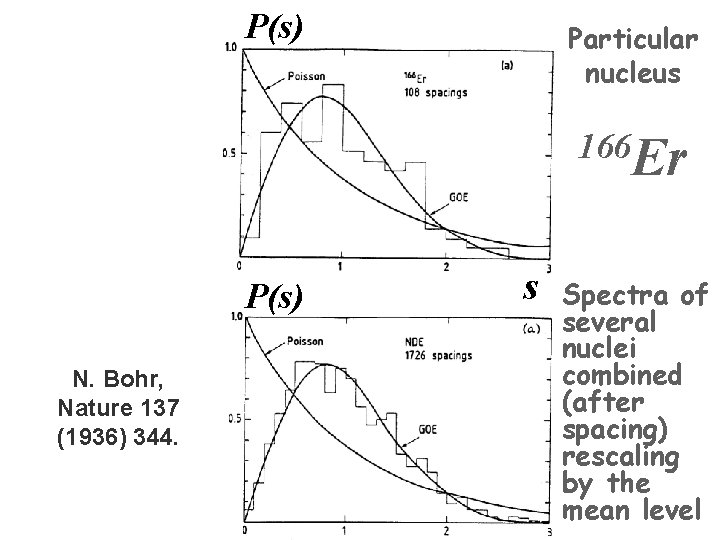
P(s) Particular nucleus 166 Er P(s) N. Bohr, Nature 137 (1936) 344. s Spectra of several nuclei combined (after spacing) rescaling by the mean level

Q: Why the random matrix theory (RMT) works so well for nuclear spectra Original answer: Later it became clear that These are systems with a large number of degrees of freedom, and therefore the “complexity” is high ? there exist very “simple” systems with as many as 2 degrees of freedom (d=2), which demonstrate RMT like spectral statistics

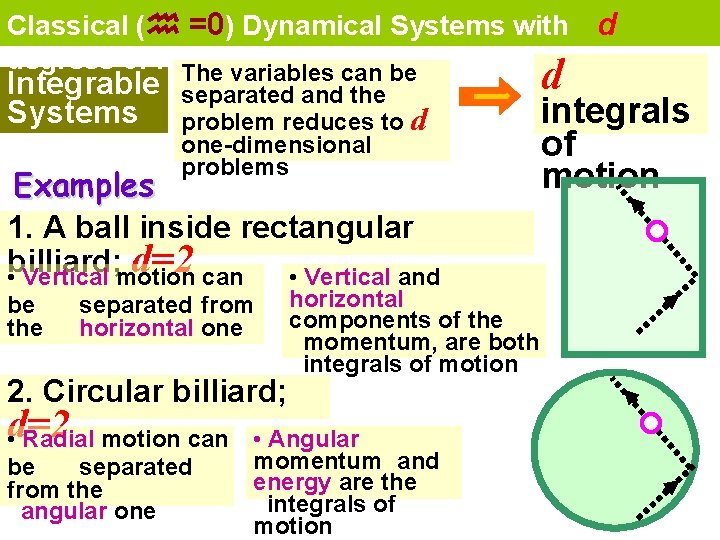
Classical (h =0) Dynamical Systems with degrees of freedom The variables can be Integrable Systems separated and the problem reduces to d one-dimensional problems Examples 1. A ball inside rectangular billiard; d=2 • Vertical motion can • Vertical and be the separated from horizontal one 2. Circular billiard; d=2 • Radial motion can be separated from the angular one horizontal components of the momentum, are both integrals of motion • Angular momentum and energy are the integrals of motion d d integrals of motion

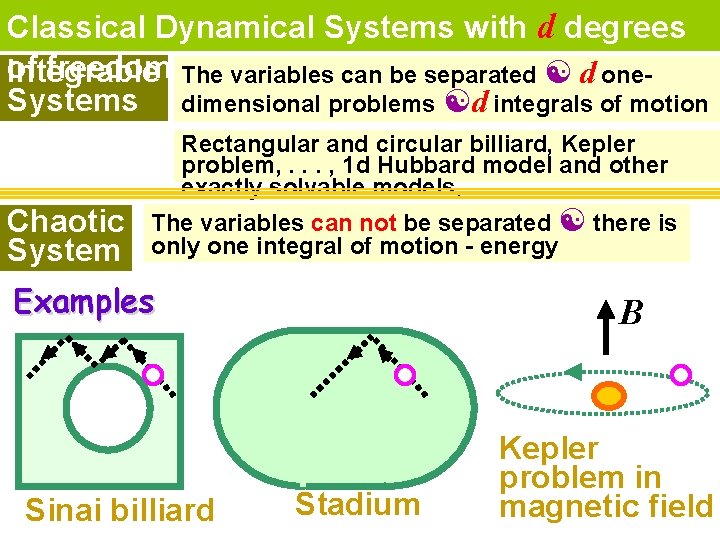
Classical Dynamical Systems with d degrees of freedom The variables can be separated [ d one. Integrable Systems dimensional problems [d integrals of motion Rectangular and circular billiard, Kepler problem, . . . , 1 d Hubbard model and other exactly solvable models, . . The variables can not be separated [ there is only one integral of motion - energy Chaotic System s Examples Sinai billiard B Stadium Kepler problem in magnetic field

Classical Chaos h =0 • Nonlinearities • Exponential dependence on the original conditions (Lyapunov exponents) • Ergodicity Quantum description of any System with a finite number of the degrees of freedom is a linear problem – Shrodinger equation Q: What does it mean Quantum

Bohigas – Giannoni – Schmit conjecture Chaotic classical analog Wigner- Dyson spectral statistics No quantum numbers except energy

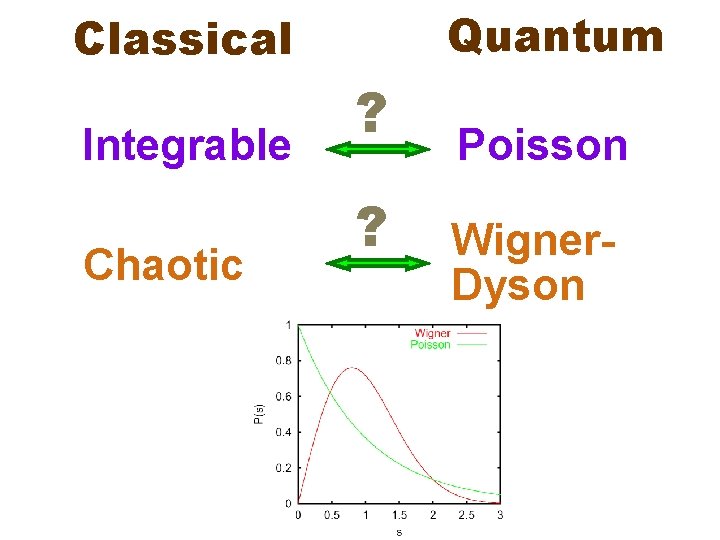
Quantum Classical Integrable Chaotic ? ? Poisson Wigner. Dyson

Lecture 1. 2. Localization beyond real space

Kolmogorov – Arnold – Moser (KAM) theory A. N. Kolmogorov, Dokl. Akad. Nauk SSSR, 1954. Proc. 1954 Int. Congress of Mathematics, North. Holland, 1957 Andrey Kolmogorov Vladimir Arnold Jurgen Moser Integrable classical Hamiltonian Separation of variables: action-angle variables d , d>1: sets of

1 D classical motion – action-angle variables

Kolmogorov – Arnold – Moser (KAM) theory A. N. Kolmogorov, Dokl. Akad. Nauk SSSR, 1954. Proc. 1954 Int. Congress of Mathematics, North. Holland, 1957 Integrable classical Hamiltonian Separation of variables: action-angle variables d , d>1: sets of Quasiperiodic motion: set of the frequencies, which are in general incommensurate. Actions are integrals of motion Andrey Kolmogorov …=> Vladimir Arnold Jurgen Moser tori

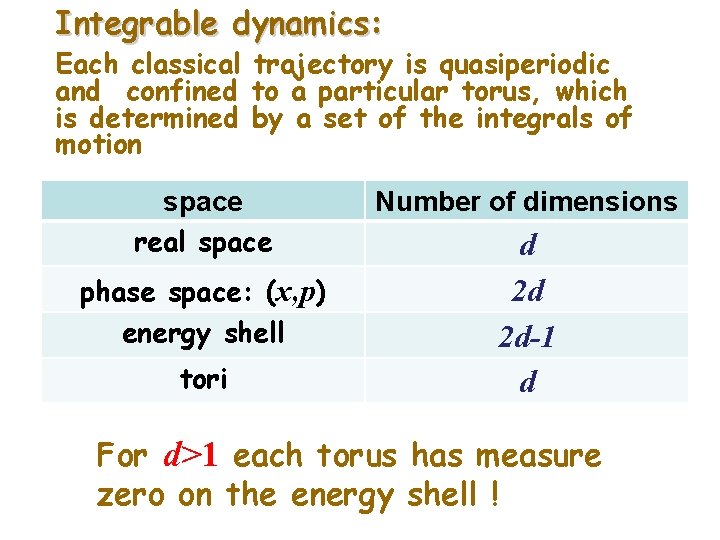
Integrable dynamics: Each classical trajectory is quasiperiodic and confined to a particular torus, which is determined by a set of the integrals of motion space real space phase space: (x, p) energy shell tori Number of dimensions d 2 d 2 d-1 d For d>1 each torus has measure zero on the energy shell !

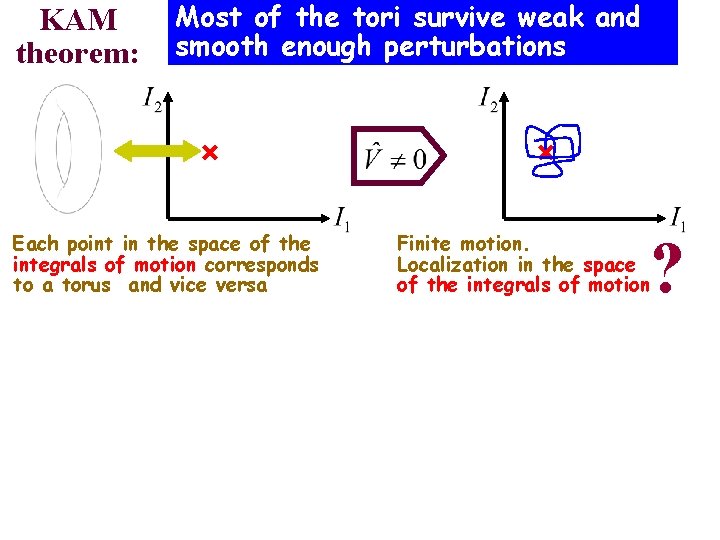
Kolmogorov – Arnold – Moser (KAM) theory A. N. Kolmogorov, Integrable classical Hamiltonian Dokl. Akad. Nauk SSSR, 1954. Proc. 1954 Int. Congress of Mathematics, North. Holland, 1957 Separation of variables: variables d , d>1: sets of action-angle Quasiperiodic motion: set of the frequencies, which are in general incommensurate Actions are integrals of motion …=> Q: Andrey Kolmogorov Vladimir Arnold Jurgen Moser A: Will an arbitrary weak perturbation of the integrable Hamiltonian destroy the tori and make the motion ergodic (when each point at the energy shell will be reached sooner or later) ? Most of the tori survive KAM weak and smooth enough theorem perturbations

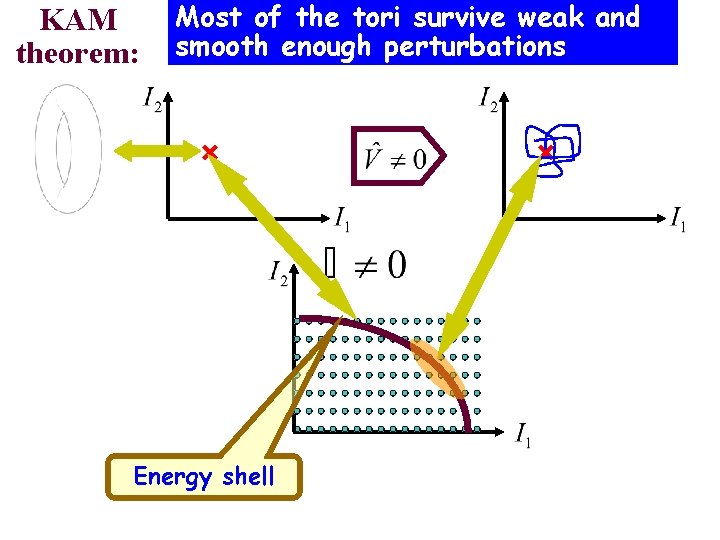
KAM theorem: Most of the tori survive weak and smooth enough perturbations Each point in the space of the integrals of motion corresponds to a torus and vice versa ? Finite motion. Localization in the space of the integrals of motion

KAM theorem: Most of the tori survive weak and smooth enough perturbations Energy shell

Consider an integrable system. Each state is characterized by a set of quantum numbers. It can be viewed as a point in the space of quantum numbers. The whole set of the states forms a lattice in this space. A perturbation that violates the integrability provides matrix elements of the hopping between different sites (Anderson model !? ) Weak enough hopping: Localization - Poisson Strong hopping: transition to Wigner-Dyson

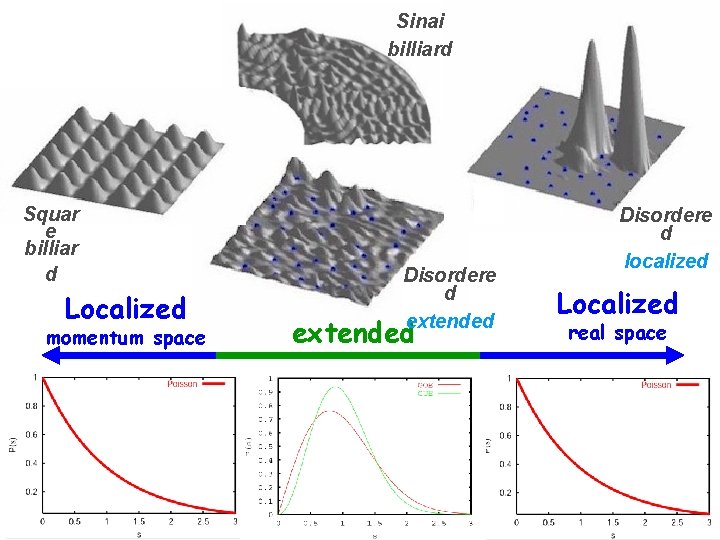
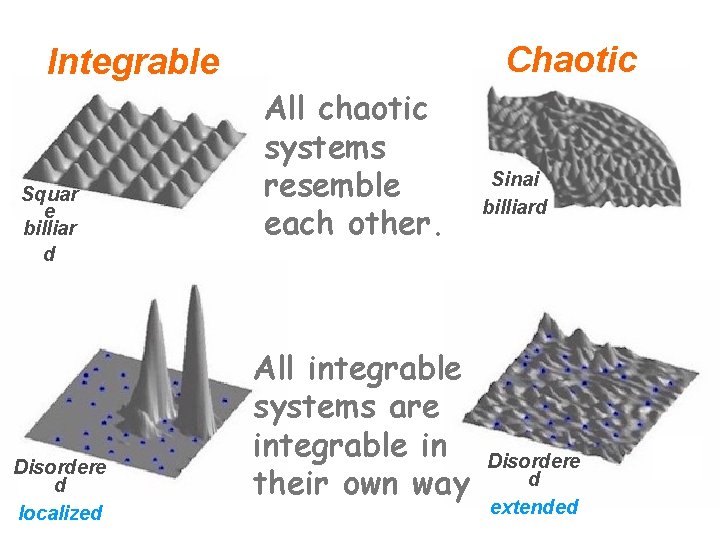
Sinai billiard Squar e billiar d Localized momentum space Disordere d extended Disordere d localized Localized real space

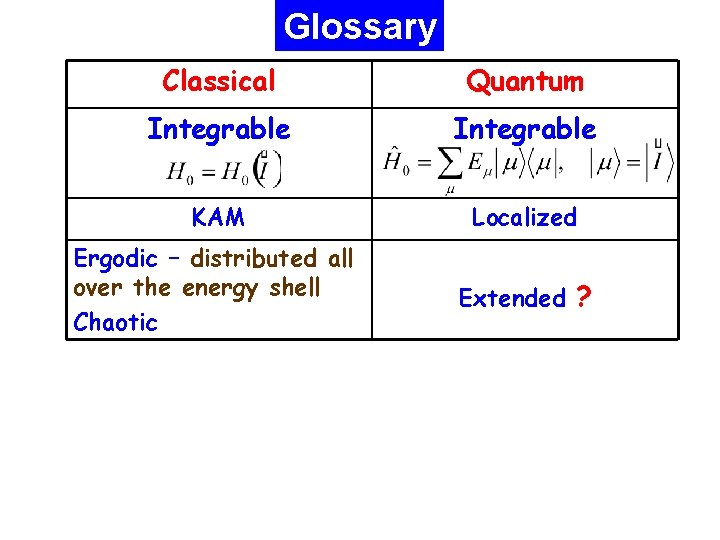
Glossary Classical Quantum Integrable KAM Localized Ergodic – distributed all over the energy shell Chaotic Extended ?

Extended Level repulsion, anticrossings, Wigner-Dyson spectral statistics states: Localized Poisson spectral statistics states: Invariant (basis independent) definition

Chaotic Integrable Squar e billiar d Disordere d localized All chaotic systems resemble each other. All integrable systems are integrable in their own way Sinai billiard Disordere d extended

Q: Consider a finite system of quantum particles, e. g. , fermions. Let the one-particle spectra be chaotic (Wigner. Dyson). ? What is the statistics of the many-body spectra? a. The particles do not interact with each other. Poisson: individual energies are conserving quantum numbers. b. The particles do interact. ? ?

Lecture 2. 3. Many-Body excitation in finite systems

Decay of a quasiparticle with an energy Landau Fermi liquid Fermi Sea in

Quasiparticle decay rate at T = 0 in a clean Fermi Liquid. I. d=3 Fermi Sea Reasons: • At small the energy transfer, , is small and the integration over and gives the factor 2. ………………………………… • The momentum transfer, q , is large and thus the scattering probability at given and does not depend on , or

Quasiparticle decay rate at T = 0 in a clean Fermi Liquid. II. Low dimensions Small moments transfer, q , become important at low dimensions because the scattering probability is proportional to the squared time of the interaction, (qv. F. )-2 1/q e v. F

Quasiparticle decay rate at T Fermi Liquid. Quasiparticle decay at =T 0 =in 0 ainclean a clean Fermi Liquid. Fermi Sea Conclusions: 1. For d=3, 2 from it follows that , i. e. , that the qusiparticles are well determined and the Fermi-liquid approach is applicable. 2. For d=1 is of the order of , i. e. , that the Fermi-liquid approach is not valid for 1 d systems of interacting fermions. Luttinger liquids

Decay of a quasiparticle with an energy Fermi liquid in Landau Quantum dot – zero-dimensional case -w 1+w 1 Fermi Sea

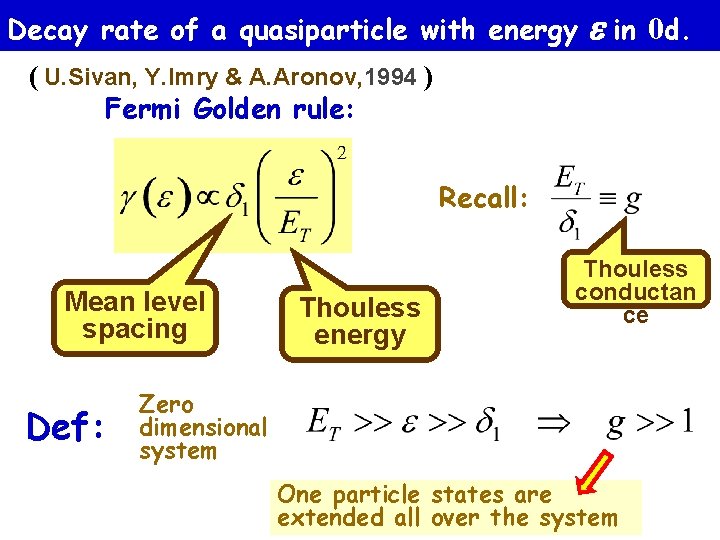
Decay of a quasiparticle with an energy Fermi liquid in Landau Quantum dot – zero-dimensional case -w 1+w Decay rate of a quasiparticle with energy Y. Imry & A. Aronov, 1994 ) ( U. Sivan, Fermi Golden rule: 1 Fermi Sea Mean level spacing Thouless energy

Decay rate of a quasiparticle with energy in 0 d. ( U. Sivan, Y. Imry & A. Aronov, 1994 ) Fermi Golden rule: Recall: Mean level spacing Def: Thouless energy Thouless conductan ce Zero dimensional system One particle states are extended all over the system

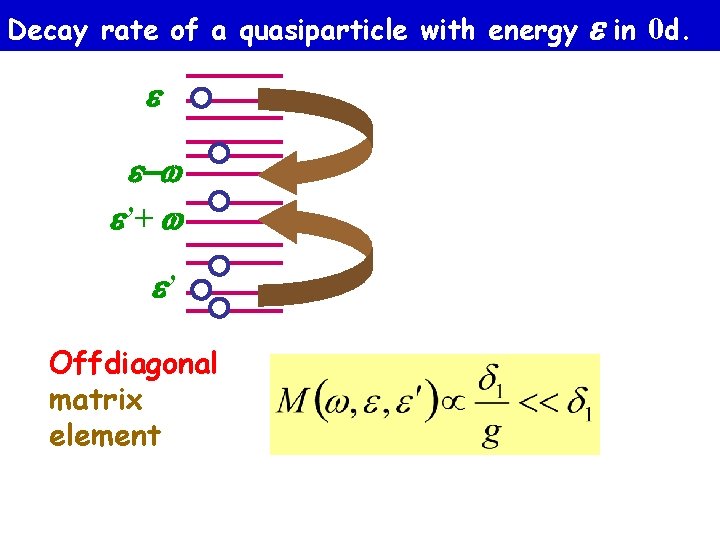
Decay rate of a quasiparticle with energy in 0 d. Problem: zero-dimensional case -w 1+w 1 Fermi Sea one-particle spectrum is discrete equation 1 2 = ’ 1 ’ 2 can not be satisfied exactly Recall: in the Anderson model the site-to-site hopping does not conserve the energy

Decay rate of a quasiparticle with energy ’+ ’ Offdiagonal matrix element in 0 d.

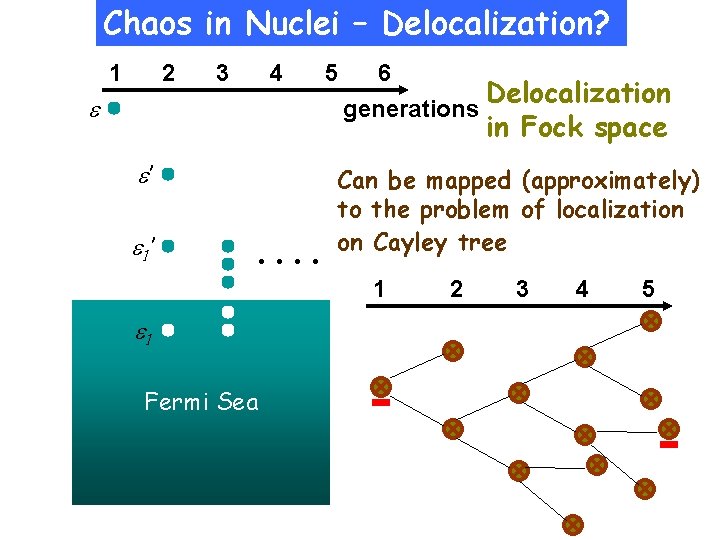
Chaos in Nuclei – Delocalization? 1 2 3 4 5 6 Delocalization generations in Fock space ’ 1’ . . Can be mapped (approximately) to the problem of localization on Cayley tree 1 1 Fermi Sea 2 3 4 5

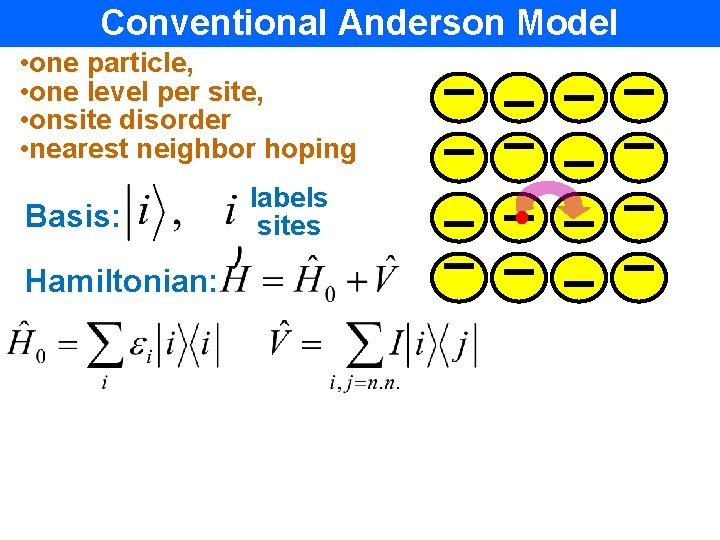
Conventional Anderson Model • one particle, • one level per site, • onsite disorder • nearest neighbor hoping Basis: Hamiltonian: labels sites

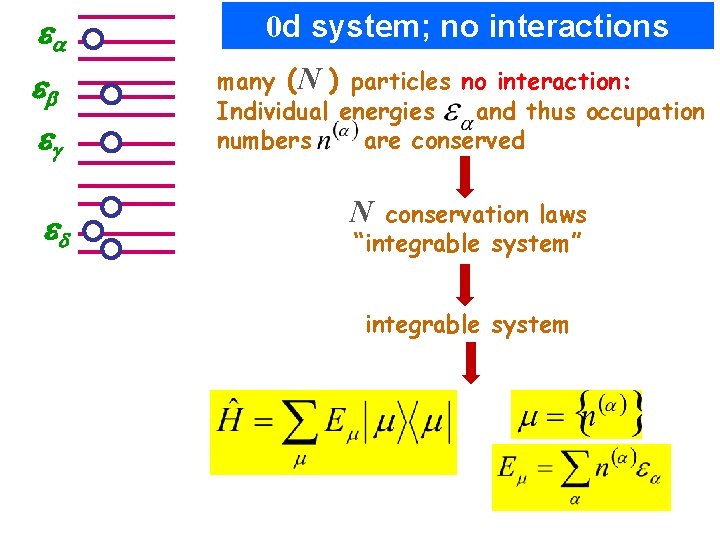
a 0 d system; no interactions b many (N ) particles no interaction: Individual energies and thus occupation numbers are conserved g d N conservation laws “integrable system” integrable system

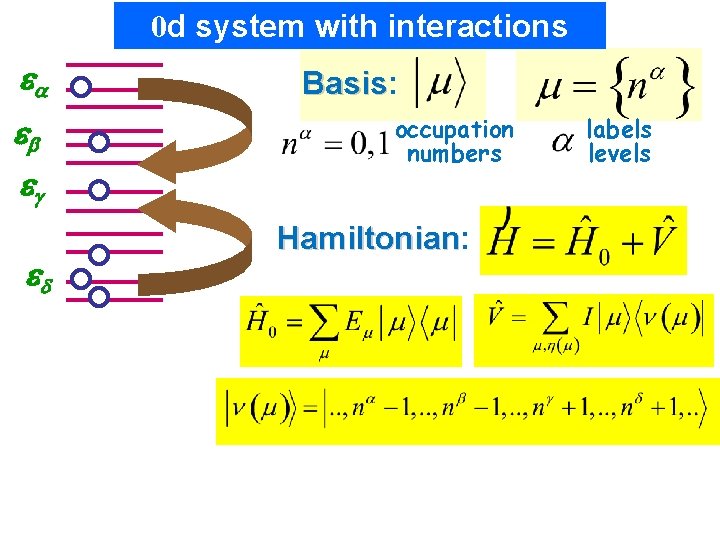
0 d system with interactions a b g d Basis: Basis occupation numbers Hamiltonian: Hamiltonian labels levels

Conventional Anderson Model Basis: Many body Andersonlike Model Basis: Basis labels levels labels sites “nearest neighbors”: occupation numbers

Isolated quantum dot – 0 d system of fermions Exact many-body states: Ground state, excited states Exact means that the imaginary part of the energy is zero! Quasiparticle excitations: Finite decay rate Q: What is the connection ?

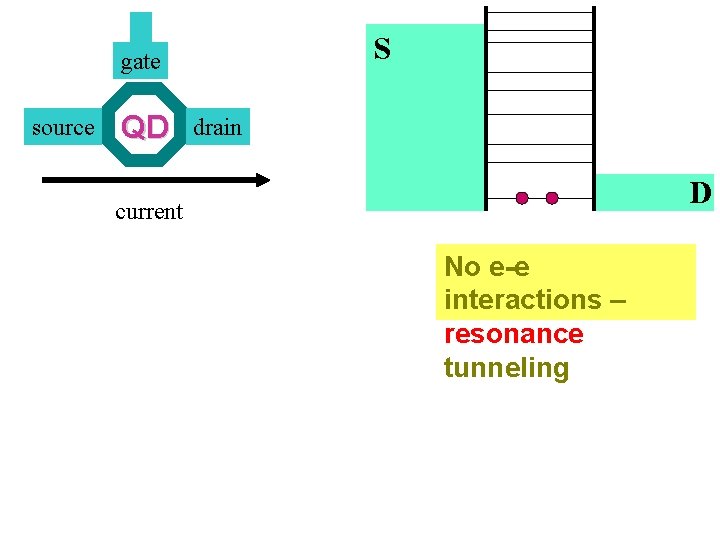
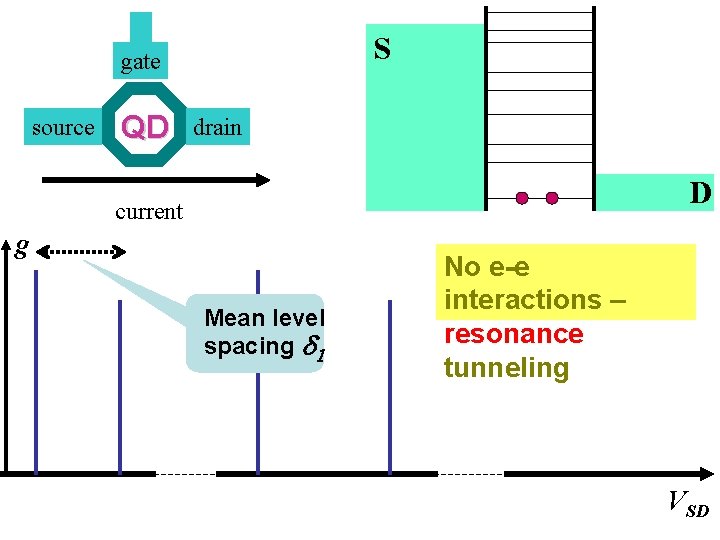
S gate source QD drain D current No e-e interactions – resonance tunneling

S gate source QD drain D current g Mean level spacing d 1 No e-e interactions – resonance tunneling VSD

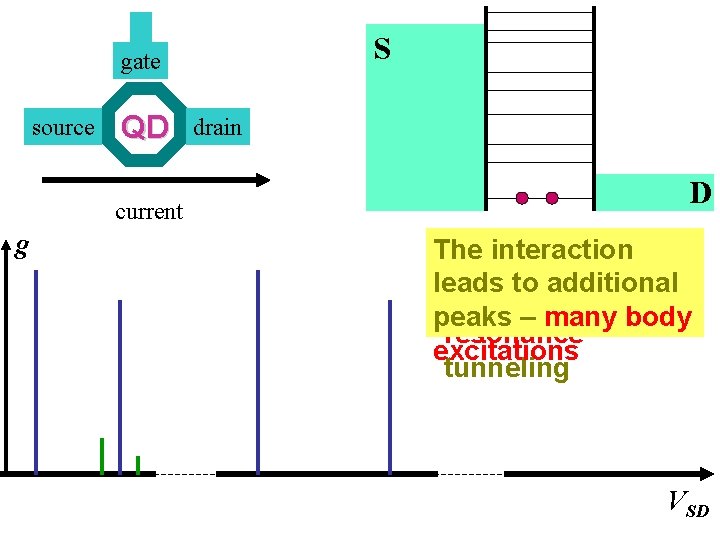
S gate source QD current g drain D The interaction No e-e leads to additional interactions – peaks – many body resonance excitations tunneling VSD

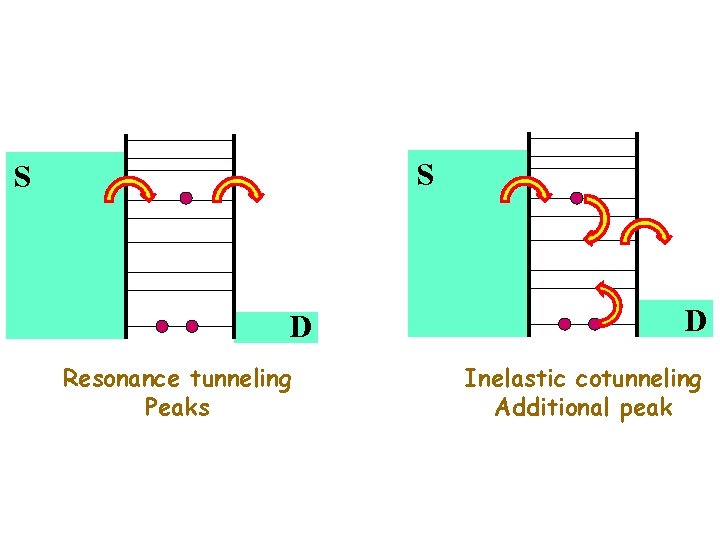
S S D Resonance tunneling Peaks D Inelastic cotunneling Additional peak

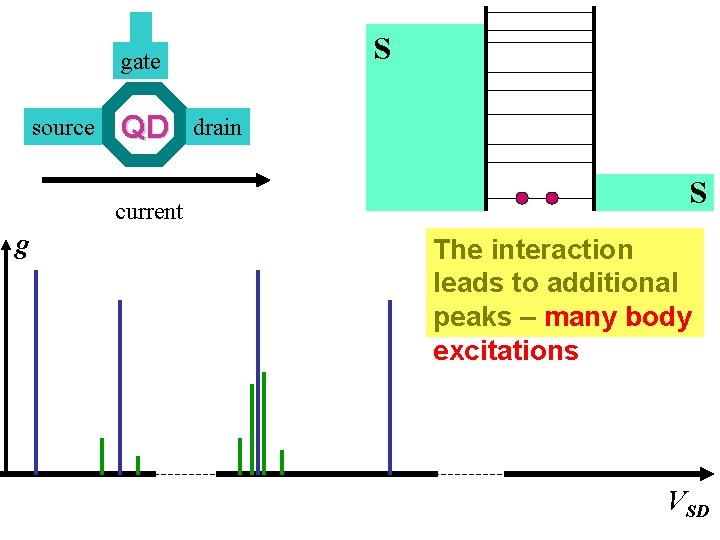
S gate source QD current g drain S The interaction leads to additional peaks – many body excitations VSD

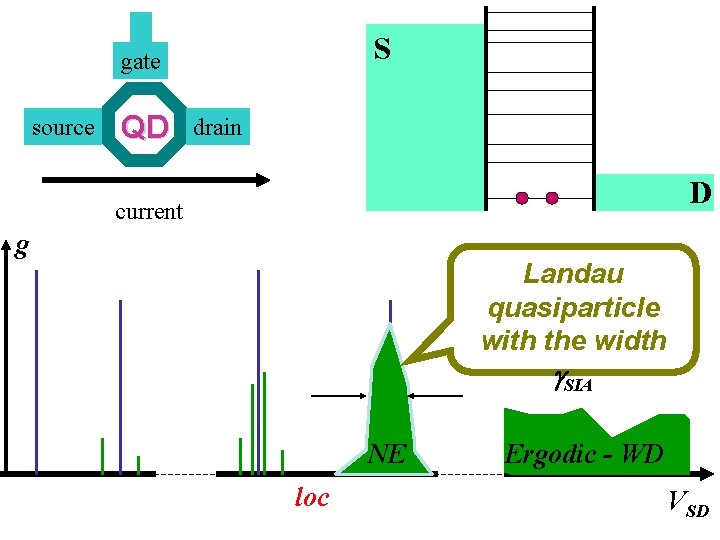
S gate source QD drain D current g Landau quasiparticle with the width g. SIA NE loc Ergodic - WD VSD

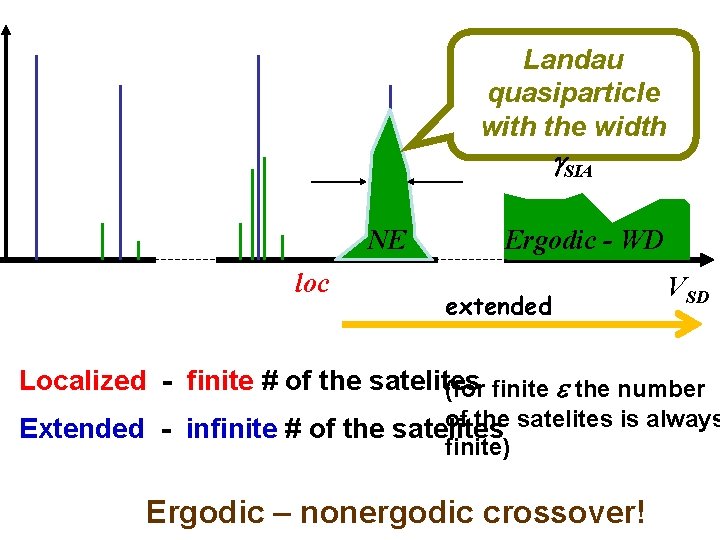
Landau quasiparticle with the width g. SIA NE loc Ergodic - WD extended VSD Localized - finite # of the satelites (for finite the number of the satelites is always Extended - infinite # of the satelites finite) Ergodic – nonergodic crossover!

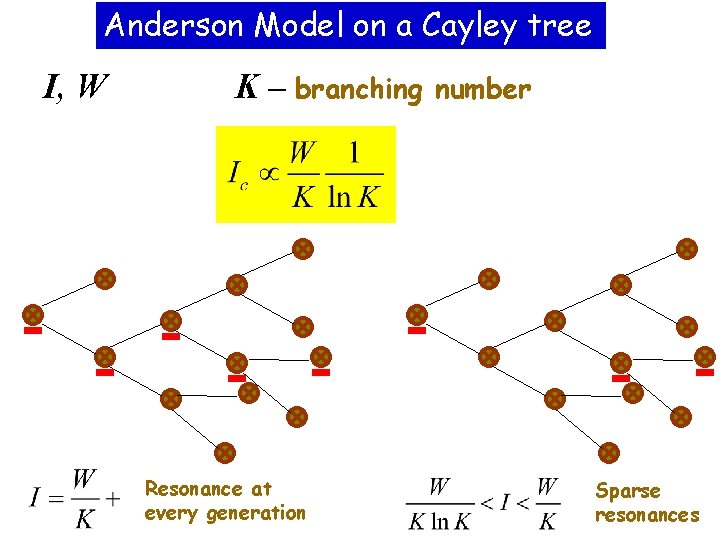
Anderson Model on a Cayley tree

Anderson Model on a Cayley tree I, W K – branching Resonance at every generation number Sparse resonances

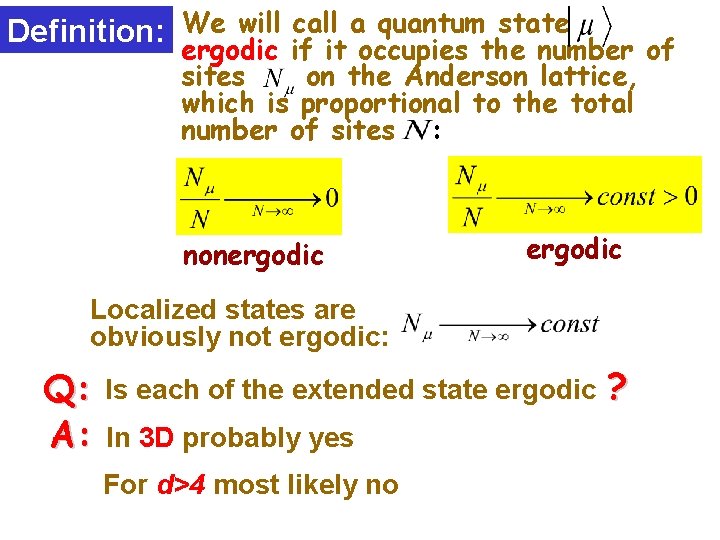
Definition: We will call a quantum state ergodic if it occupies the number of sites on the Anderson lattice, which is proportional to the total number of sites : nonergodic Localized states are obviously not ergodic: Q: A: Is each of the extended state ergodic In 3 D probably yes For d>4 most likely no ?

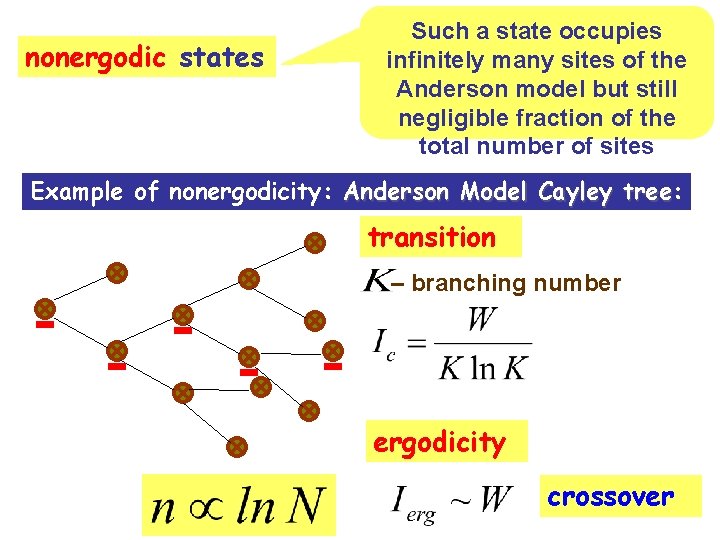
nonergodic states Such a state occupies infinitely many sites of the Anderson model but still negligible fraction of the total number of sites Example of nonergodicity: Anderson Model Cayley tree: tree transition – branching number ergodicity crossover

Resonance is typically far localized Typically there is no resonance at the next step nonergodic Typically there is a resonance at every step nonergodic Typically each pair of nearest neighbors is at ergodic