DISK ACCRETION in YOUNG STARS BROWN DWARFS THEORY

DISK ACCRETION in YOUNG STARS & BROWN DWARFS: THEORY vs OBSERVATIONS Subhanjoy Mohanty (Imperial College London) Frank H. Shu (UC San Diego), Isabelle Baraffe (ENS Lyon)
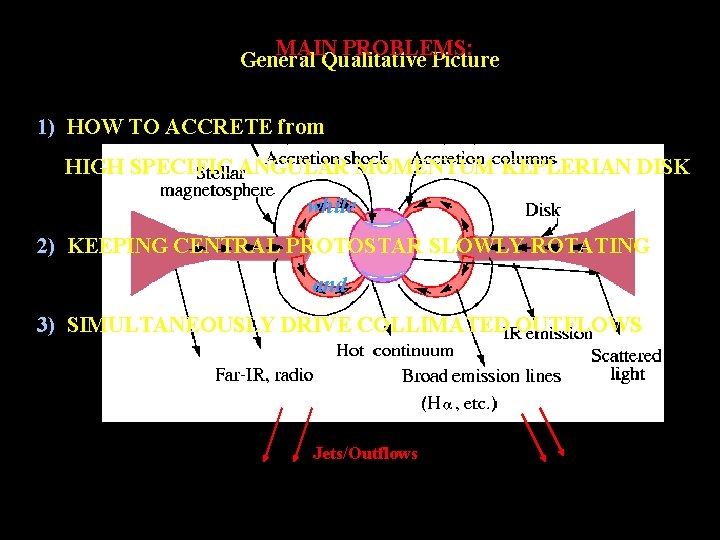
MAIN PROBLEMS: General Qualitative Picture 1) HOW TO ACCRETE from HIGH SPECIFIC ANGULAR MOMENTUM KEPLERIAN DISK while 2) KEEPING CENTRAL PROTOSTAR SLOWLY ROTATING and 3) SIMULTANEOUSLY DRIVE COLLIMATED OUTFLOWS Jets/Outflows
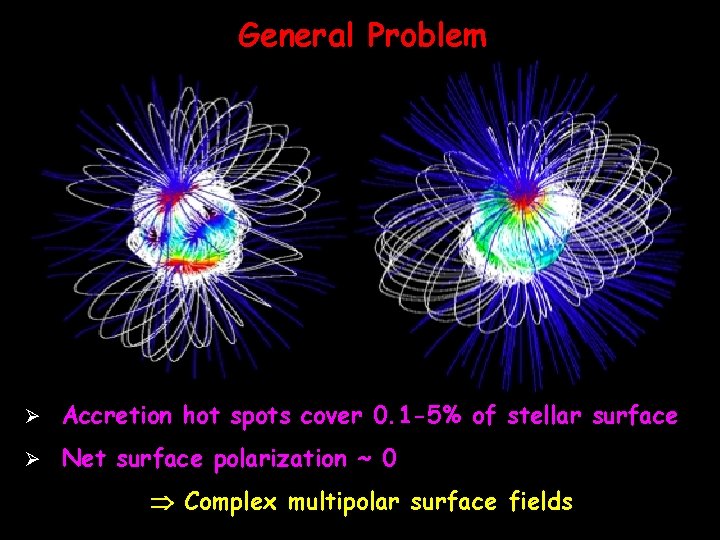
General Problem All current magnetospheric accretion models assume a dipolar stellar magnetic field. However Polarization studies: stellar surface field NOT dipolar. Ø Average field strengths: ~few k. G (Zeeman) Ø Strong polarization in lines formed in accretion shock accretion occurs along ordered field lines BUT Ø Accretion hot spots cover 0. 1 -5% of stellar surface Ø Net surface polarization ~ 0 Complex multipolar surface fields
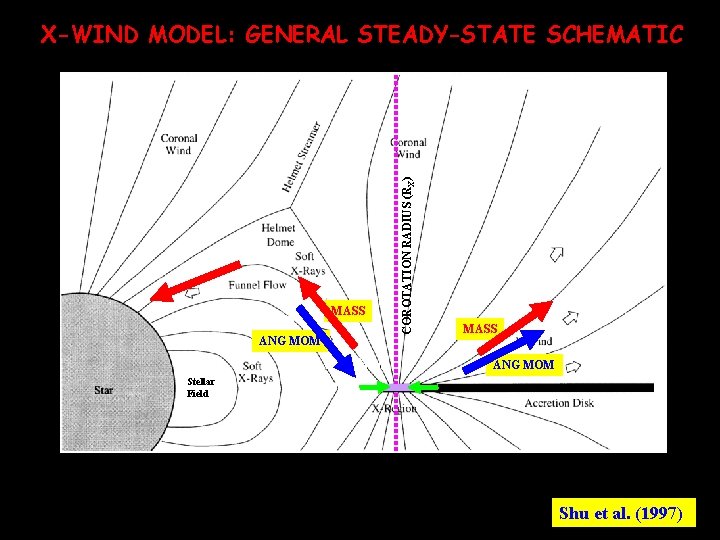
MASS ANG MOM COROTATION RADIUS (RX) X-WIND MODEL: GENERAL STEADY-STATE SCHEMATIC MASS ANG MOM Stellar Field Shu et al. (1997)

GENERALIZED X-WIND MODEL • Trapped Flux at X-point: Φt • Fraction of trapped flux involved in accretion (funnel flow): Φt / 3 • Same field lines flow into hot spot: (2π R*2) Fh Bh = Φt / 3 • Angular momentum removed by trapped flux from funnel flow gas: • (1 -J ) R 2Ω = ∮[r (T • n) ^ d. S] (Φ 2 / R ) (1 -f) M D * X X t X • Disk-locking: ΩX = Ω* = (GM*/RX 3)1/2 general: Fh R*2 Bh (G M* M • D / Ω*)1/2 • dipole: R*3 Bh (G M*5/3 MD / Ω*7/3)1/2 Mohanty & Shu (2008)
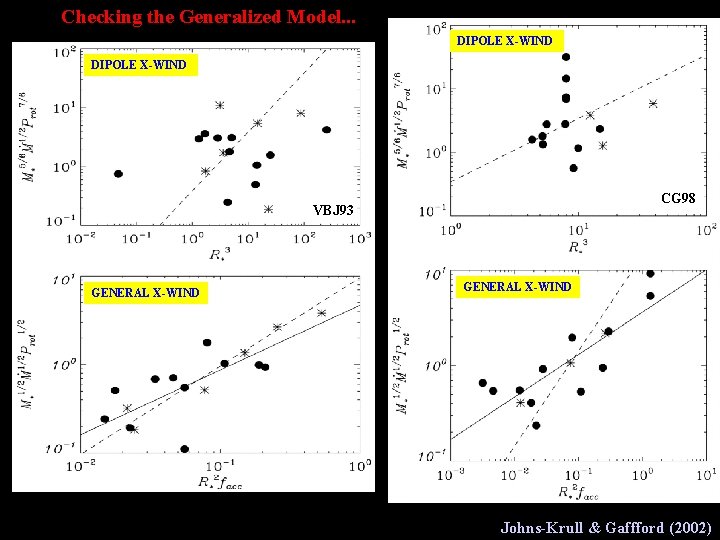
Checking the Generalized Model. . . DIPOLE X-WIND CG 98 VBJ 93 GENERAL X-WIND Johns-Krull & Gaffford (2002)

The Cases of V 2129 Oph & BP Tau (Mdot, Fh, Bh directly measured simultaneously) V 2129 Oph: • M = 1. 35 M , R = 2. 4 R , Mdot = 1 X 10 M /yr • P = 6. 53 day R (=R ) = 6. 67 R • B = 2 k. G, F = 5% measured F B = 100 G • Multipole X-wind equation (with f = 1/3, ß = 1. 21): * * * -8 COROTATION h X h * (Donati et al. 2007) h h predicted Fh. Bh = 79 G BP Tau: • M = 0. 8 M , R = 1. 95 R , Mdot = 3 X 10 M /yr • P = 7. 6 day R (=R ) = 7. 5 R • B = 9 k. G, F = 2% measured F B = 180 G • Multipole X-wind equation (with f = 1/3, ß = 1. 21): * * h * COROTATION h -8 X * h h (Donati et al. 2008) predicted Fh. Bh = 170 G
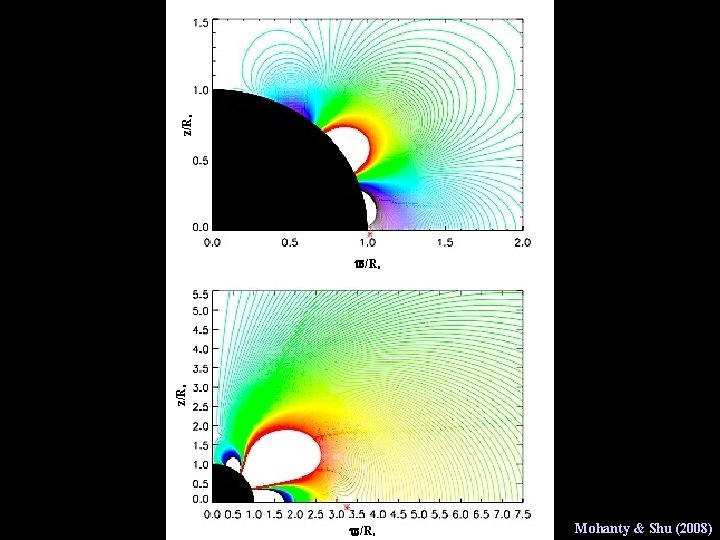
z/R* Mohanty & Shu (2008)
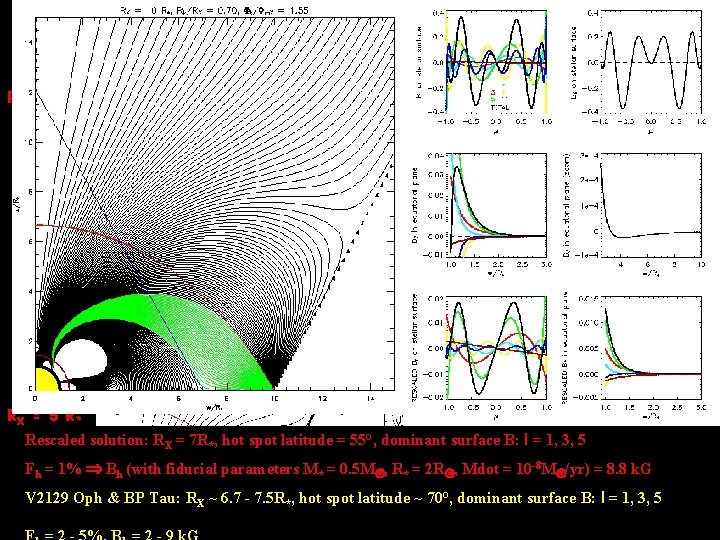
RX = 10 R* RX = 5 R * Rescaled solution: RX = 7 R*, hot spot latitude = 55°, dominant surface B: l = 1, 3, 5 RX = 7. 5 R* RX = 2 R * Fh = 1% Bh (with fiducial parameters M* = 0. 5 M , R* = 2 R , Mdot = 10 -8 M /yr) = 8. 8 k. G V 2129 Oph & BP Tau: RX ~ 6. 7 - 7. 5 R*, hot spot latitude ~ 70°, dominant surface B: l = 1, 3, 5 Mohanty & Shu (2008)

X-Wind Conclusions • X-Wind theory: Main ingredient is trapped flux; • Dipole field not necessary; makes general unique prediction consistent with obs. • Multipole fields can match both the observational constraints on surface field and the X-point geometry Requirement for flux trapping: Field diffusivity (η) << Gas viscosity (ν) Prandtl # (= ν/η) >> 1 (consistent with Prandtl # from MRI analysis: Shu et al. 2007)

Disk Winds • Requires fast (turbulent) diffusion, and Prandtl # ~ 1, for sufficient mass-loading and flinging • disk-gas radial velocity ~ sonic (e. g. , Ferreira et al 95) • If disk-wind is primary accretion mechanism out to, say, 300 AU (Td ~ 20 K), then entire disk empties onto star in ~ 5000 years • If disk wind over small inner region of disk, then inner regions of disk will be very optically thin (e. g. , Combet et al. ‘ 08). Does not appear consistent with majority of CTTS (except perhaps transition disks)

Effect of accretion on evolutionary models Assumptions: Phenomenological approach (Gallardo, Baraffe, Chabrier 2009) • Accretion through a disk or magnetospheric accretion (non spherical) ---> disturbs only a small portion of the surface Lphot=4πR 2(1 - ) Teff 4 -----> 0 • Accreted matter brings internal energy: GMdot. M/R (accretion from a thin disk: ≤ 0. 5) Fraction absorbed by the central object radiated away absorbed intrinsic ≤ 1 mass increase
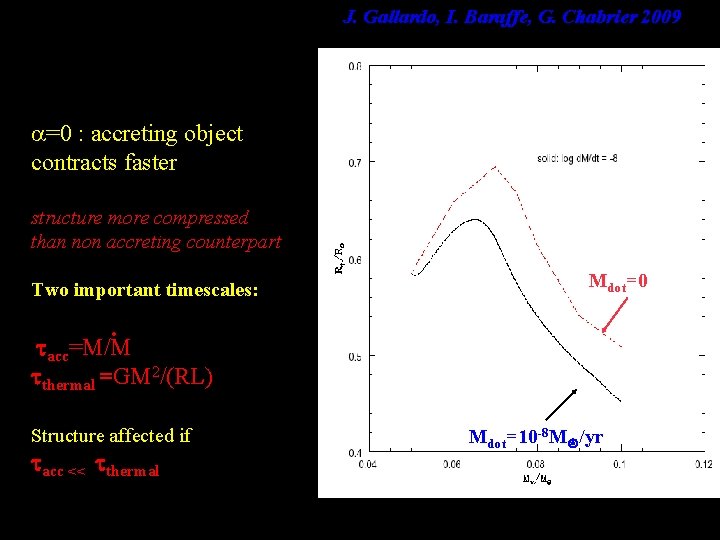
J. Gallardo, I. Baraffe, G. Chabrier 2009 =0 : accreting object contracts faster structure more compressed than non accreting counterpart Two important timescales: Mdot=0 . acc=M/M thermal =GM 2/(RL) Structure affected if acc << thermal Mdot=10 -8 M /yr
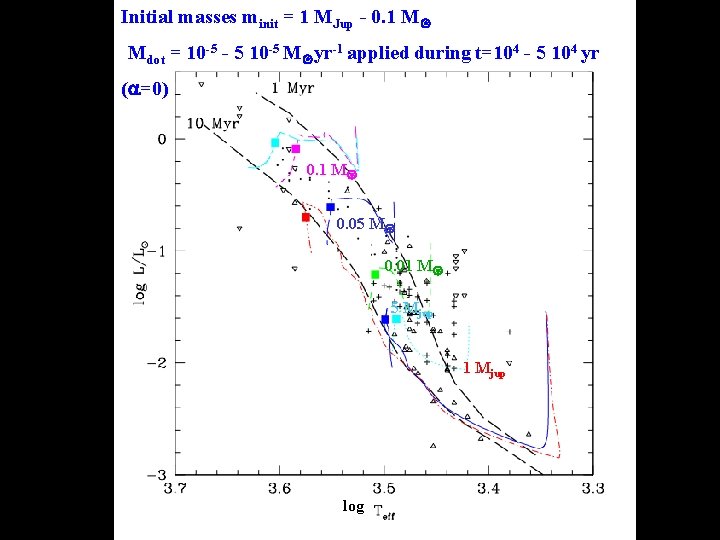
Initial masses minit = 1 MJup - 0. 1 M Mdot = 10 -5 - 5 10 -5 M yr-1 applied during t=104 - 5 104 yr ( =0) 0. 1 M 0. 05 M 0. 01 M 5 Mjup 1 Mjup log

Conclusion on accretion effects • Initial rates Mdot ≤ 10 -6 M yr-1 produce small luminosity scatter in HRD at ages of ~ Myr • A scenario based on very early stages of non steady accretion (series of short episodes of vigorous accretion Mdot 10 -4 M yr-1 of a few 100 yr): - naturally produces a spread in the HRD at ages of a few Myr: provides an explanation for the presence of underluminous objects in star formation regions which « look » significantly older - Produces a significant radius spread as a function of Teff - Consistent with recent observations of protostars and revised lifetimes of class 0 - I

Conclusion on accretion effects • Concept of a birthline not valid: depends on the accretion history • IMF of very young (<~ few Myr) clusters/SFRs is elusive!! • Accretion effects cannot explain the objects that appear significantly above the non-accreting tracks; possibly need to invoke magnetic field effects on convection (a la 2 M 0535: young eclipsing binary in ONC with Teff reversal: Mohanty et al. 2009). This is further bad news for IMF determination in very young regions

THE END
FUTURE • X-wind theory: Include viscous torque (if disk fields present); Tilted Fields; Non-Axisymmetry; • Simulations: non-dipole fields with flux-trapping • Disk + B-fields Theory: understand disk viscosity vs. resistivity better (require MRI simulations with global and non-zero fields) • Observations required!!!! : Disk field strength + geometry, Disk inner edge / jet field geometry, Jet launch region (e. g. , from rotation, vel. , density…)

Why Important? • End-game of star formation, IMF: • Accretion + Outflow + Blowout of surrounding envelope by outflow Final mass of star • Injection of turbulence from combined outflows into cloud Regulated star formation • Disk accretion lifetime + disk physics planet formation timescale + formation/migration physics

Connection with Planet Formation • Mass accretion vs. Outflow rates • Size of stellar field / disk interaction region • Location and extent of jet launching region… SPECIFICS of ACCRETION / OUTFLOW DEPEND on: Ø Efficiency of disk magneto-rotational instability (MRI) Ø Turbulent viscosity vs. Field diffusivity from MRI DISK PARAMETERS, Ø Degree of disk ionization Ø Thickness of ionized surface vs. dead zone in interior Ø Stellar field geometry Ø Strength of stellar field vs. Global disk fields… v Efficiency of grain sedimentation & coagulation v Efficiency of core-accretion near ice line v Orbital migration & Eccentricity pumping… which also CONTROL: PLANET FORMATION / MIGRATION
Insights from Brown Dwarfs Mohanty et al. , 2009, in prep.

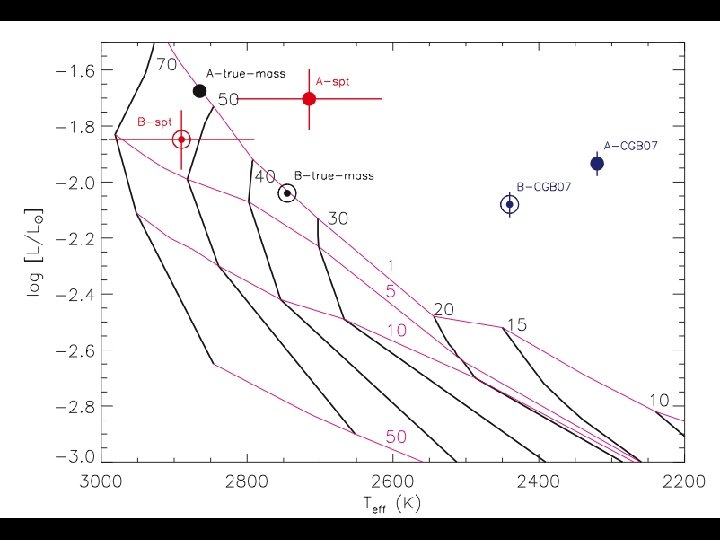
• Truncation radius from rotation velocity: Ω* = (GM*/RX 3)1/2 (RX/R*) = (GM*/v*2 R*)1/3 CTTS: RX ~ 6 --7 R* , BDs: RX ~ 4 --5 R* • Remember: F B = f h h 1/2 (G M* MD 2 / R*5)1/4 (RX / R*)3/4 in CTTS: Fh. Bh ~ 77 G , in BDs: Fh. Bh ~ 17 G If Fh roughly same in both cases (few %), Bh in BDs ~ 1/5 Bh in CTTS: ~ 2 k. G in BDs: ~ 500 G Observationally true!! (Reiners & Basri 2009, submitted)

Maybe expected: Field VLMS/BDs: ~ few k. G, 1/3 R* young: few 100 G BUT WHY? ? ? Why should field generation mechanism produce field strengths just right to truncate disk at about the same RX/R* in T Tauri stars and BDs, with vastly different masses and accretion rates? ? ? Mystery thickens, or solution: The RX/R* in CTTS (~6 -7) and in BDs (~4 -5) imply: TDISK ~ 1200 K Minimum temperature for good field/disk coupling!!

ACCRETION DISKS + JETS AROUND YOUNG STARS: REAL IMAGES

ACCRETION DISK AROUND A YOUNG STAR: ARTIST’S IMPRESSION
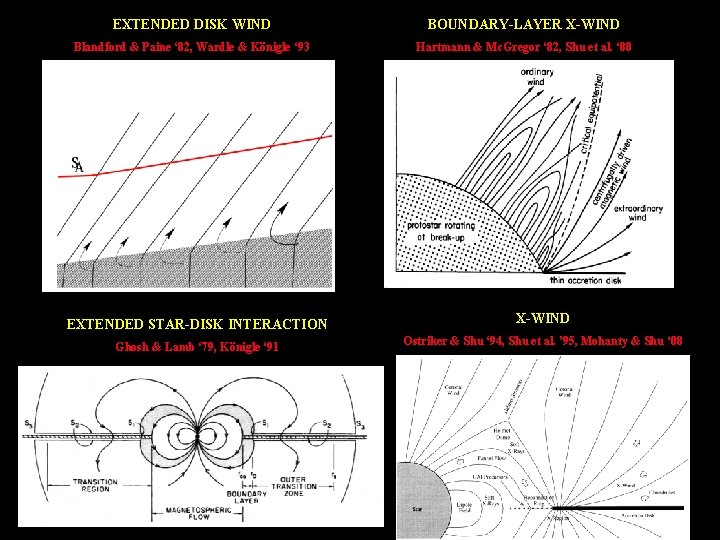
EXTENDED DISK WIND BOUNDARY-LAYER X-WIND Blandford & Paine ‘ 82, Wardle & Königle ‘ 93 Hartmann & Mc. Gregor ‘ 82, Shu et al. ‘ 88 EXTENDED STAR-DISK INTERACTION X-WIND Ghosh & Lamb ‘ 79, Königle ‘ 91 Ostriker & Shu ‘ 94, Shu et al. ’ 95, Mohanty & Shu ‘ 08

CONSTANT of PROPORTIONALITY • • • With: f MW / MD and ∫ 01 ( )d , where B = ( ) u (i. e. , =mean magnetic field to mass flux ratio in X-wind) • • Wind dynamics: Φt / 3 = 2 f 1/2 (G M* MD 2 RX 3)1/4 • Recall: (2π R*2) Fh Bh = Φt / 3 and ΩX = Ω* = [GM*/RX 3]1/2 • • Fh Bh = f 1/2 Bnorm (RX / R*)3/4 where Bnorm (G M* MD 2 / R*5)1/4 • F R 2 B = Φ / 6 = f 1/2(GM M • /Ω )1/2 h * h t * D * • Angular momentum balance in X-region (entering = leaving): • R 2Ω = (1 -f) M • J R 2Ω + f M • J R 2Ω + M D X X D * X X D W X X f = (1 - J* - ) / (JW - J*) • Assume: J* ≈ 0 , ≈ 0 JW ≈ 1 / f ; f = 1/3 = 1. 21 (Cai et al. 2008) Mohanty & Shu (2008)
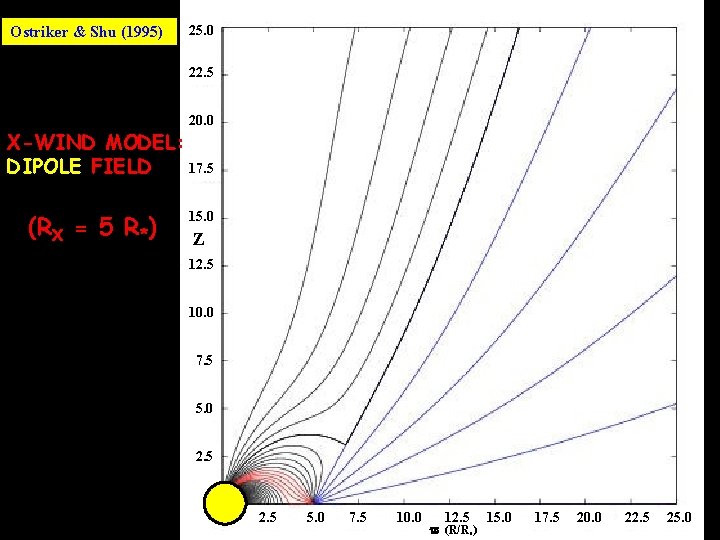
Ostriker & Shu (1995) 25. 0 22. 5 20. 0 X-WIND MODEL: DIPOLE FIELD 17. 5 (RX = 5 R*) 15. 0 Z 12. 5 10. 0 7. 5 5. 0 2. 5 5. 0 7. 5 10. 0 12. 5 (R/R*) 15. 0 17. 5 20. 0 22. 5 25. 0

Observational Constraints on Surface Field • Low Net Surface Polarization • High Polarization within Accretion Flow • Small Hot-Spot Covering Fraction (~few %)

2012 onwards. . : Average polarization direction of disk field 690 hrs ‘ 08 -’ 12: (toroidal or poloidal) Inner disk & surface fields First data coming in. . ESPa. DOn. S / CFHT Cornell Caltech Atacama Telescope Sims by Bessolaz et al. ’ 08 and Zanni et al. ‘ 07 2012 onwards. . : Field strength + geometry in disk + jet ALMA on 1 AU scales
- Slides: 32