Discriminative Approach for Wavelet Denoising Yacov HelOr and

Discriminative Approach for Wavelet Denoising Yacov Hel-Or and Doron Shaked I. D. C. - Herzliya HPL-Israel

Motivation – Image denoising - Can we clean Lena?

Some reconstruction problems Sapiro et. al. Images of Venus taken by the Russian lander Ventra-10 in 1975 - Can we “see” through the missing pixels?

Image Inpainting Sapiro et. al.

Image De-mosaicing - Can we reconstruct the color image?

Image De-blurring Can we sharpen Barbara?

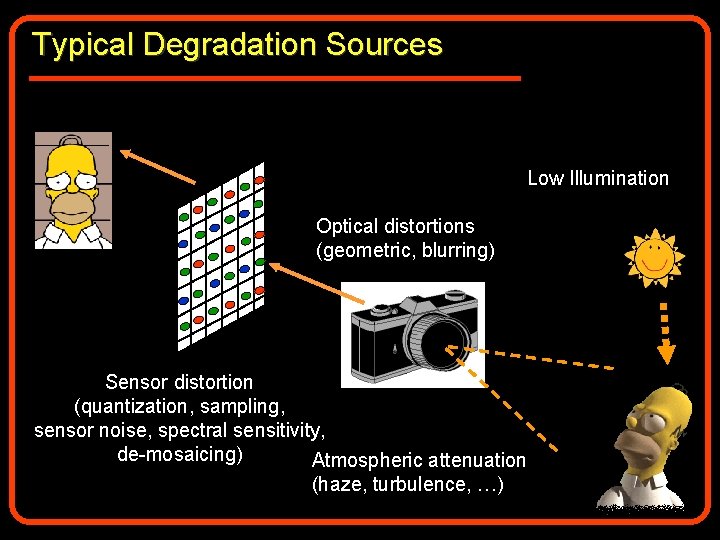
• • Inpainting De-blurring De-noising De-mosaicing • All the above deal with degraded images. • Their reconstruction requires solving an inverse problem

Typical Degradation Sources Low Illumination Optical distortions (geometric, blurring) Sensor distortion (quantization, sampling, sensor noise, spectral sensitivity, de-mosaicing) Atmospheric attenuation (haze, turbulence, …)

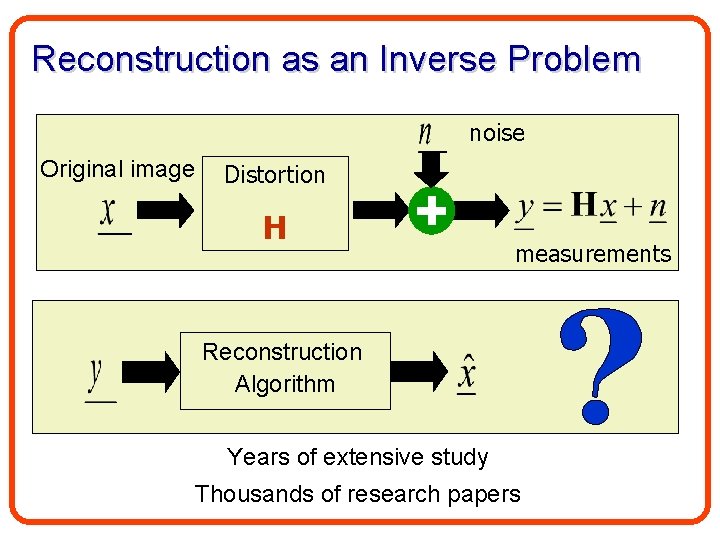
Reconstruction as an Inverse Problem noise Original image Distortion H measurements Reconstruction Algorithm Years of extensive study Thousands of research papers

• Typically: – The distortion H is singular or ill-posed. – The noise n is unknown, only its statistical properties can be learnt.

Key point: Stat. Prior of Natural Images

The Image Prior Px(x) 1 Image space 0

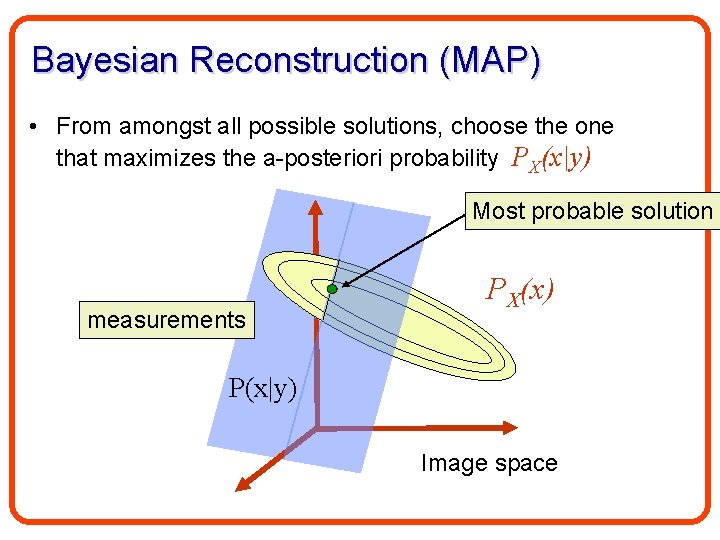
Bayesian Reconstruction (MAP) • From amongst all possible solutions, choose the one that maximizes the a-posteriori probability PX(x|y) Most probable solution measurements PX(x) P(x|y) Image space

So, are we set? Unfortunately not! • The p. d. f. Px defines a prior dist. over natural images: – Defined over a huge dim. space (1 E 6 for 1 Kx 1 K grayscale image) – Sparsely sampled. – Known to be non Gaussian. – Complicated to model.

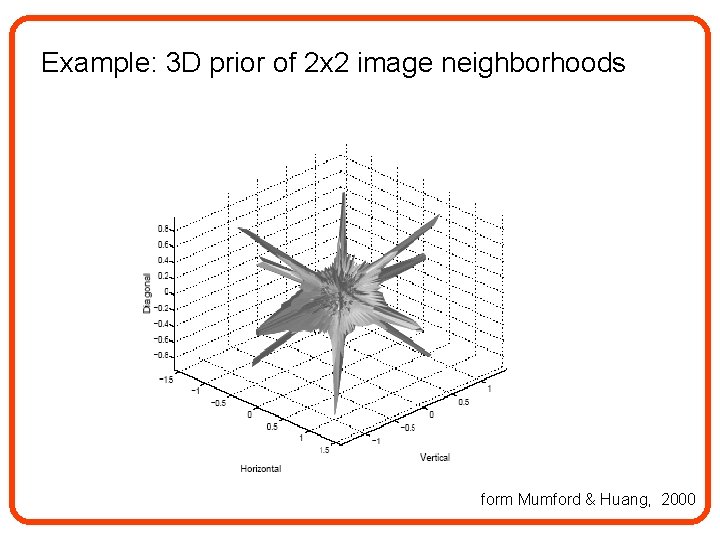
Example: 3 D prior of 2 x 2 image neighborhoods form Mumford & Huang, 2000

Marginalization of Image Prior • Observation 1: The Wavelet transform tends to decorrelate pixel dependencies of natural images. W. T.

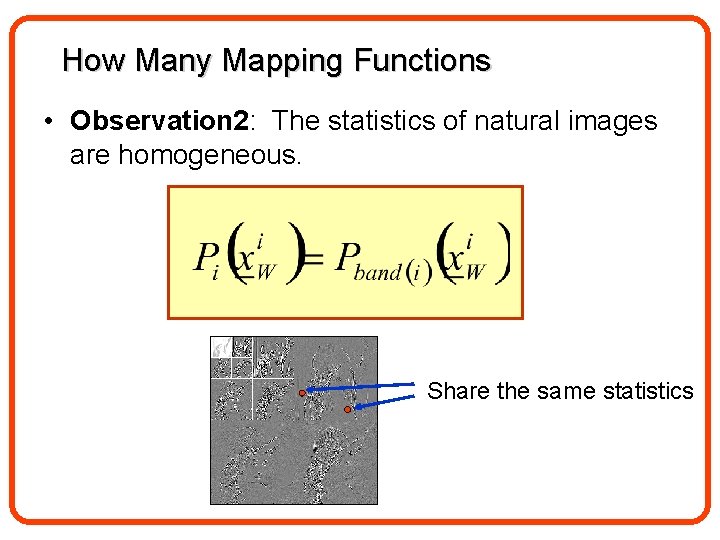
How Many Mapping Functions • Observation 2: The statistics of natural images are homogeneous. Share the same statistics

Wavelet Shrinkage Denoising Donoho & Johnston 94 (unitary case) • Degradation Model: • The MAP estimator:

• The MAP estimator gives:

• The MAP estimator diagonalizes the system: This leads to a very useful property: Scalar mapping functions:

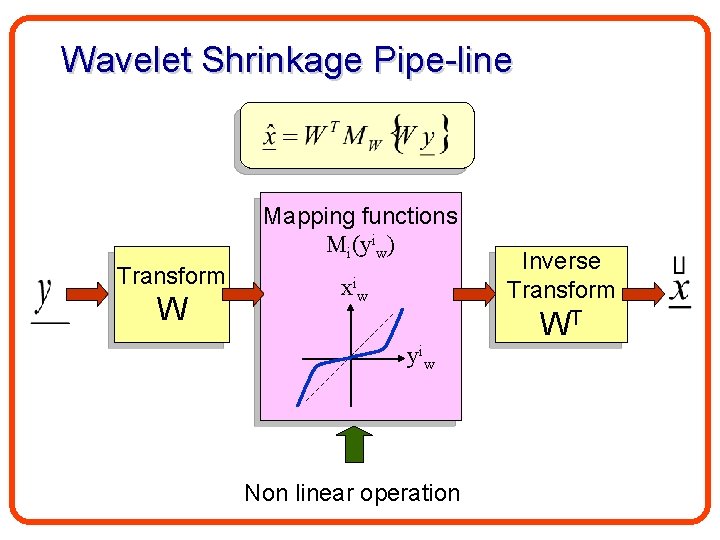
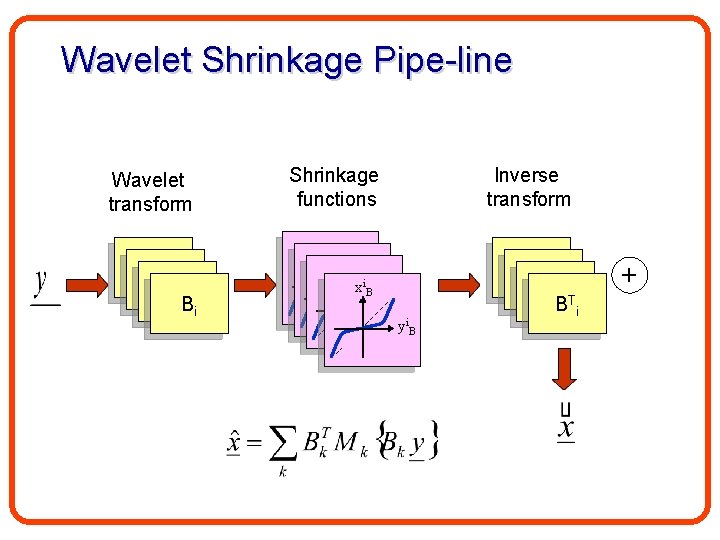
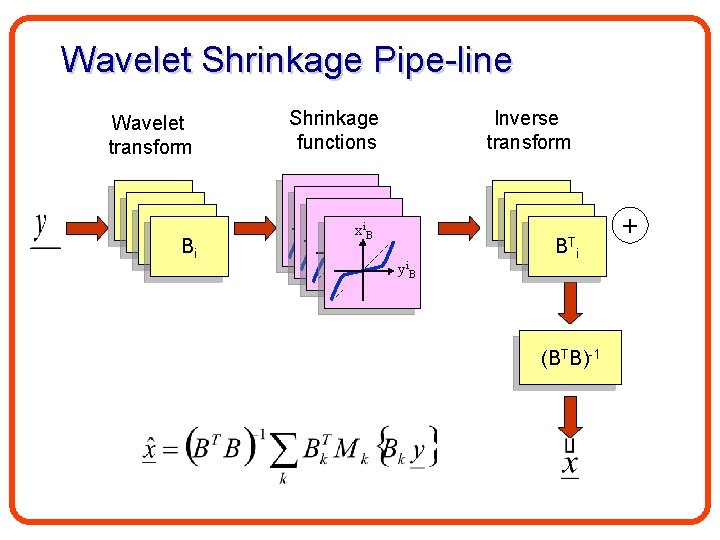
Wavelet Shrinkage Pipe-line Mapping functions Mi(yiw) Transform W xiw Inverse Transform WT yiw Non linear operation

How Many Mapping Functions? • Due to the fact that: • N mapping functions are needed for N subbands.

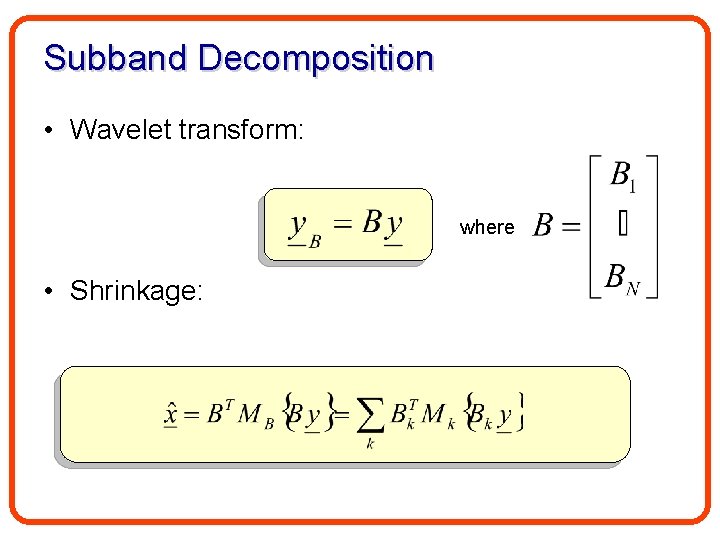
Subband Decomposition • Wavelet transform: where • Shrinkage:

Wavelet Shrinkage Pipe-line Wavelet transform B 1 B 1 Bi Shrinkage functions Inverse transform xi. B yi. B B 1 B 1 T B i +

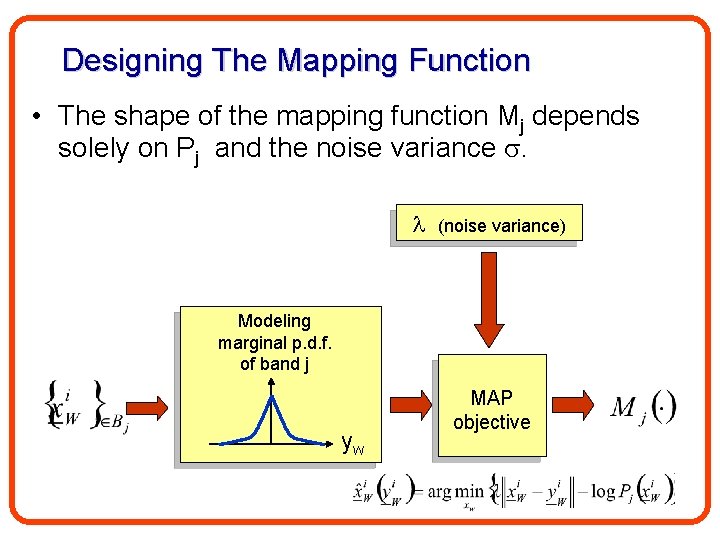
Designing The Mapping Function • The shape of the mapping function Mj depends solely on Pj and the noise variance . (noise variance) Modeling marginal p. d. f. of band j yw MAP objective

• Commonly Pj(yw) are approximated by GGD: for p<1 from: Simoncelli 99

Hard Thresholding Soft Thresholding Linear Wiener Filtering MAP estimators for GGD model with three different exponents. The noise is additive Gaussian, with variance one third that of the signal. from: Simoncelli 99

• Due to its simplicity Wavelet Shrinkage became extremely popular: – Thousands of applications. – Hundreds of related papers (984 citations of D&J paper in Google Scholar). • What about efficiency? – Denoising performance of the original Wavelet Shrinkage technique is far from the state-of-the-art results. • Why? – Wavelet coefficients are not really independent.

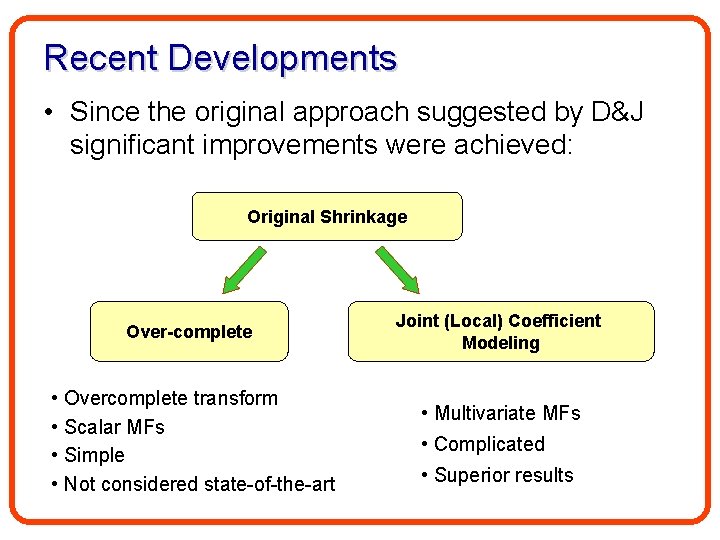
Recent Developments • Since the original approach suggested by D&J significant improvements were achieved: Original Shrinkage Over-complete • Overcomplete transform • Scalar MFs • Simple • Not considered state-of-the-art Joint (Local) Coefficient Modeling • Multivariate MFs • Complicated • Superior results

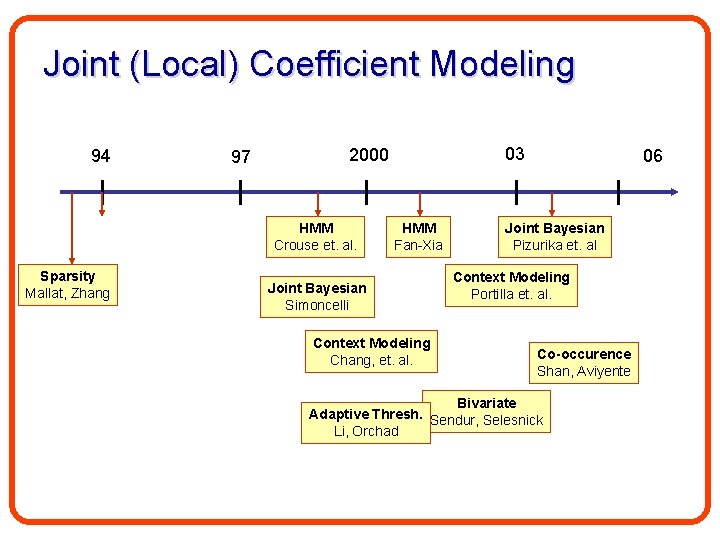
Joint (Local) Coefficient Modeling 94 97 HMM Crouse et. al. Sparsity Mallat, Zhang 03 2000 HMM Fan-Xia Joint Bayesian Simoncelli Context Modeling Chang, et. al. 06 Joint Bayesian Pizurika et. al Context Modeling Portilla et. al. Co-occurence Shan, Aviyente Bivariate Adaptive Thresh. Sendur, Selesnick Li, Orchad

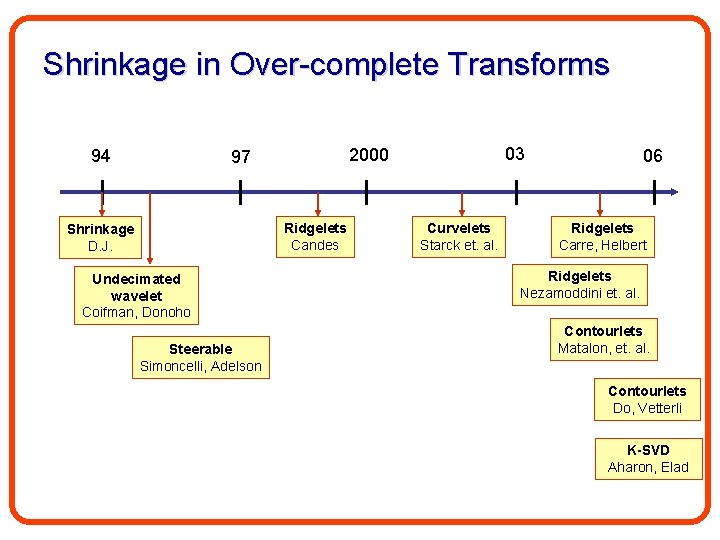
Shrinkage in Over-complete Transforms 94 Ridgelets Candes Shrinkage D. J. Undecimated wavelet Coifman, Donoho Steerable Simoncelli, Adelson 03 2000 97 Curvelets Starck et. al. 06 Ridgelets Carre, Helbert Ridgelets Nezamoddini et. al. Contourlets Matalon, et. al. Contourlets Do, Vetterli K-SVD Aharon, Elad

Over-Complete Shrinkage Denoising • Over-complete transform: where • Shrinkage: • Mapping Functions: Naively borrowed from the Unitary case.

What’s wrong with existing MFs? 1. Map criterion: – Solution is biased towards the most probable case. 2. Independent assumption: – In the overcomplete case, the wavelet coefficients are inherently dependent. 3. Minimization domain: – For the unitary case MFs optimality is expressed in the transform domain. This is incorrect in the overcomplete case. 4. White noise assumption: – Image noise is not necessarily white i. i. d.

Why unitary based MFs are being used? • Non-marginal statistics. • Multivariate minimization. • Multivariate MFs. • Non-white noise.

Suggested Approach: • Maintain simplicity – Use scalar LUTs. • Improve Efficiency – Use Over-complete Transforms. – Design optimal MFs with respect to a given set of images. – Express optimality in the spatial domain. – Attain optimality with respect to MSE.

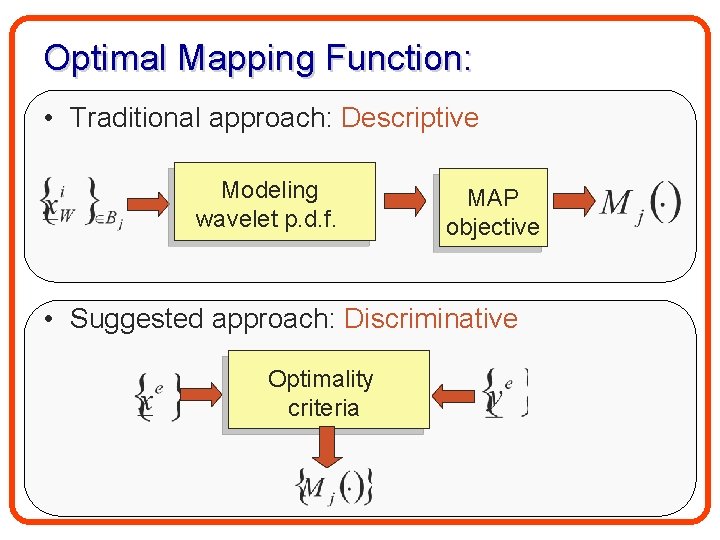
Optimal Mapping Function: • Traditional approach: Descriptive Modeling wavelet p. d. f. MAP objective • Suggested approach: Discriminative Optimality criteria

The optimality Criteria • Design the MFs with respect to a given set of examples: {xei} and {yei} • Critical problem: How to optimize the non-linear MFs

The Spline Transform • Let x R be a real value in a bounded interval [a, b). • We divide [a, b) into M segments q=[q 0, q 1, . . . , q. M] • w. l. o. g. assume x [qj-1, qj) • Define residue r(x)=(x-qj-1)/(qj-qj-1) q 0 a q 1 qj-1 qj r(x) x qj+(1 -r(x)) x=[0, , 0 x=r(x) , 1 -r(x), r(x) , 0, ]q =q. S j-1 q(x)q q. M b

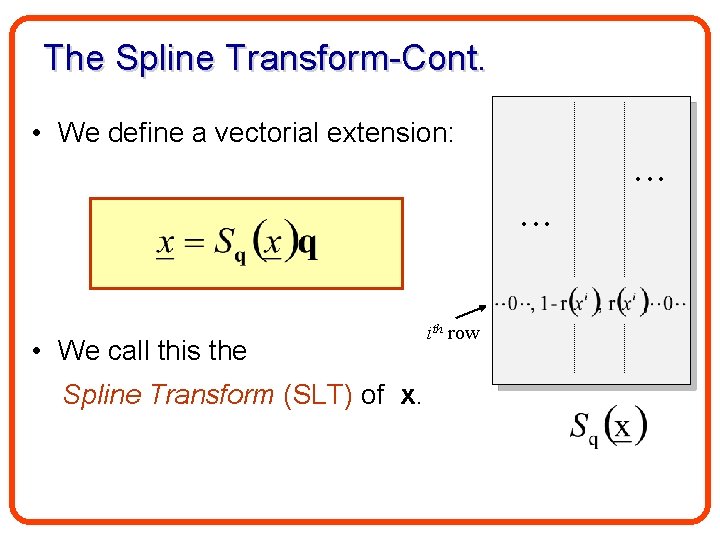
The Spline Transform-Cont. • We define a vectorial extension: • We call this the Spline Transform (SLT) of x. ith row

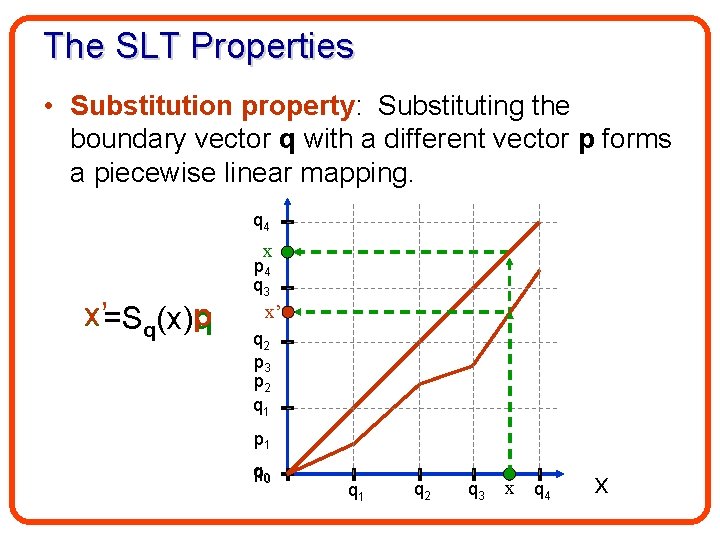
The SLT Properties • Substitution property: Substituting the boundary vector q with a different vector p forms a piecewise linear mapping. q 4 x x’=Sq(x)p q p 4 q 3 x’ q 2 p 3 p 2 q 1 p 1 q p 0 q 1 q 2 q 3 x q 4 x

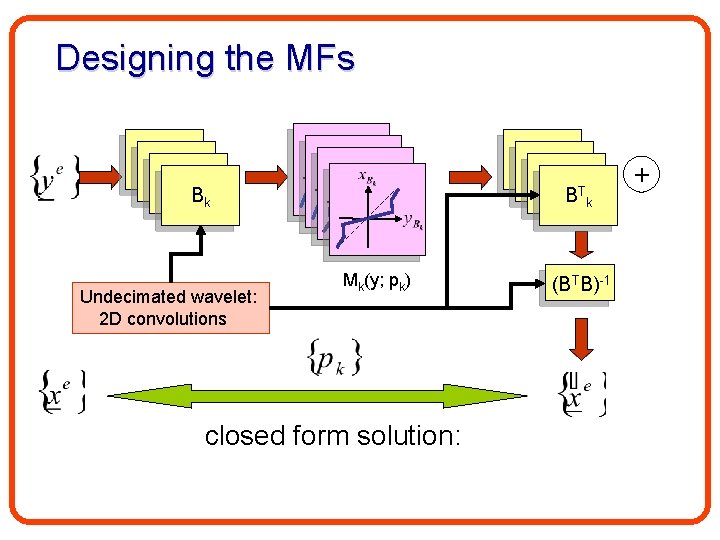
Back to the MFs Design • We approximate the non-linear {Mk} with piece-wise linear functions: • Finding {pk} is a standard LS problem with a closed form solution!

Designing the MFs B 1 B 1 Bk Undecimated wavelet: 2 D convolutions B 1 B 1 T B k Mk(y; pk) closed form solution: (BTB)-1 +

Results

Training Images

Tested Images

Simulation setup • • Transform used: Undecimated DCT Noise: Additive i. i. d. Gaussian Number of bins: 15 Number of bands: 3 x 3. . 10 x 10

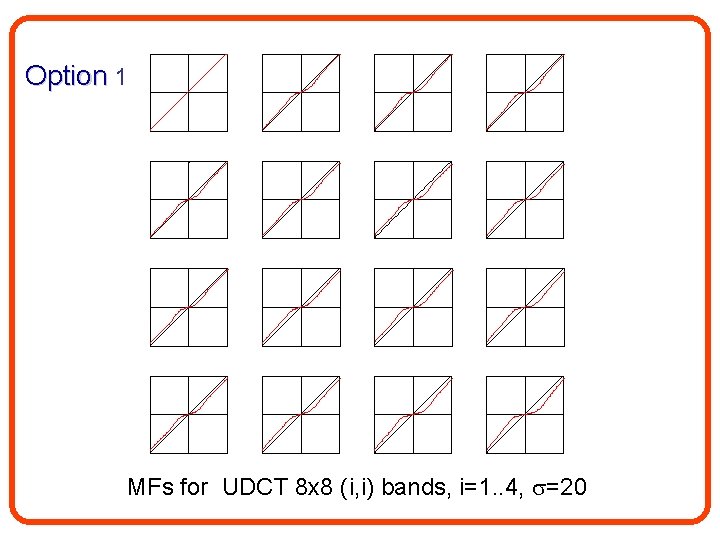
Option 1: Transform domain – independent bands BB 1 k BB 1 B 1 Tk (BTB)-1 Mk(y; pk) BB 1 k

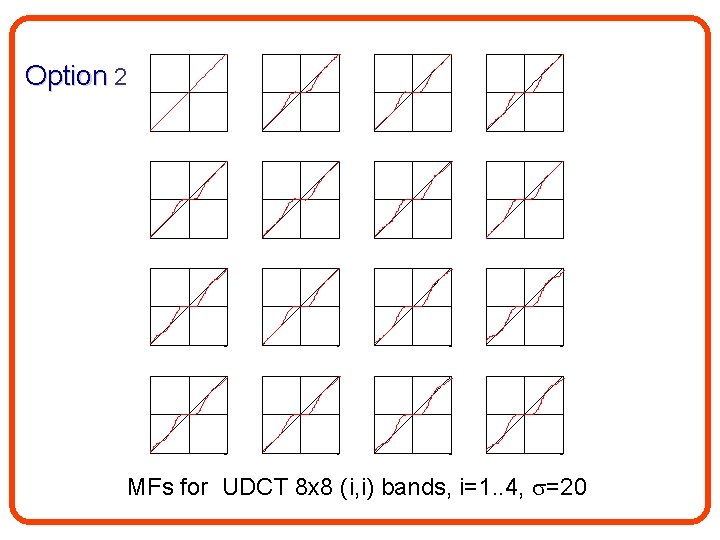
Option 2: Spatial domain – independent bands BB 1 k BB 1 B 1 Tk (BTB)-1 Mk(y; pk) BB 1 k

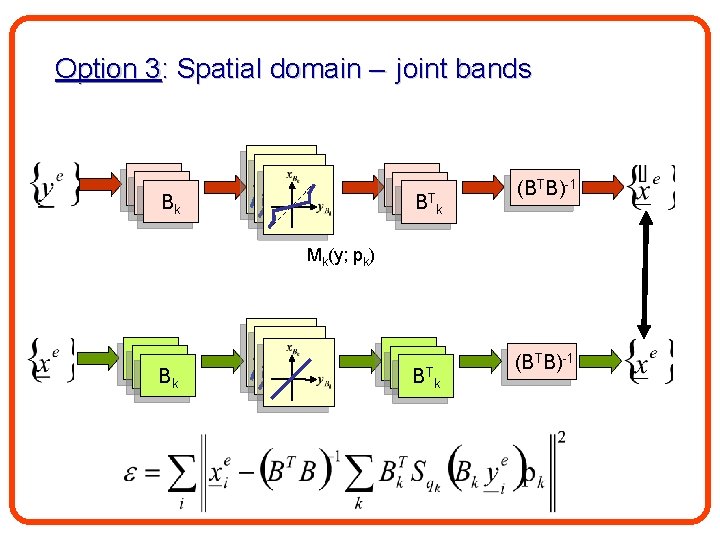
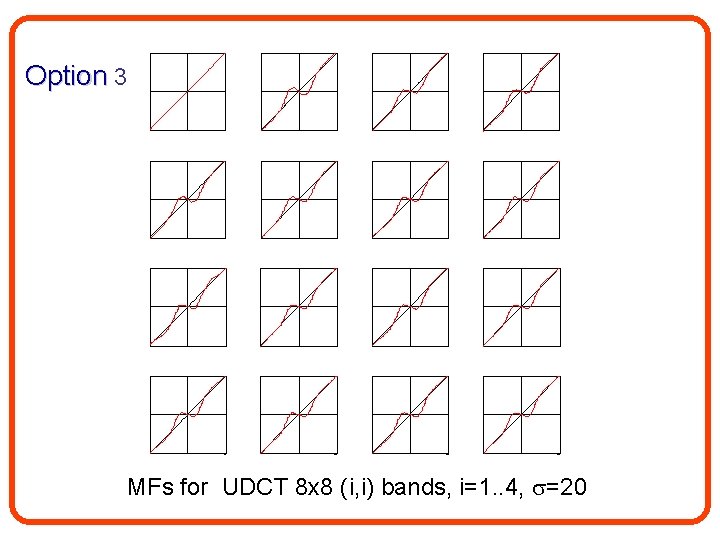
Option 3: Spatial domain – joint bands BB 1 k BB 1 B 1 Tk (BTB)-1 Mk(y; pk) BB 1 k

Option 1 Option 2 Option 3 MFs for UDCT 8 x 8 (i, i) bands, i=1. . 4, =20

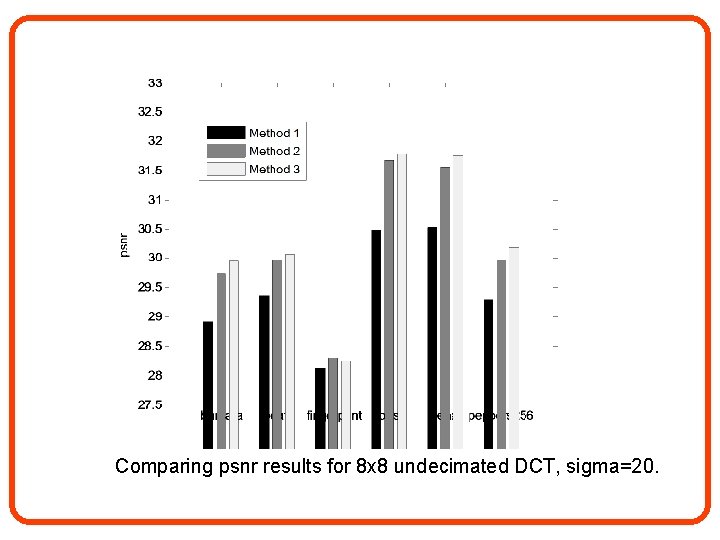
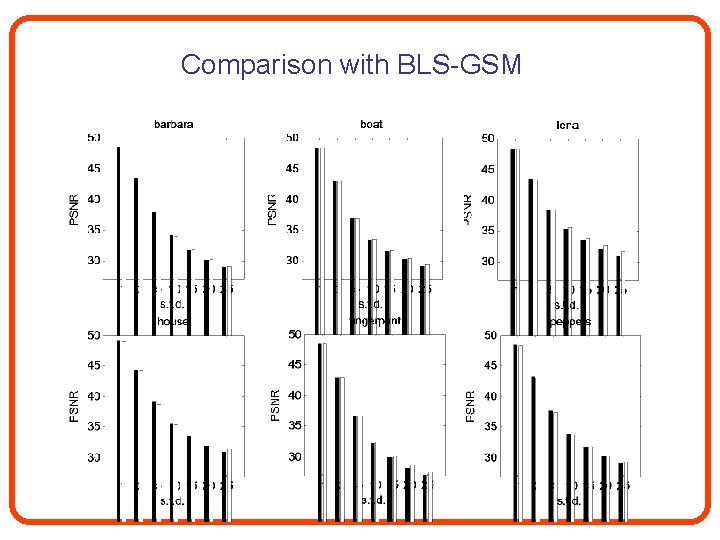
Comparing psnr results for 8 x 8 undecimated DCT, sigma=20.

8 x 8 UDCT =10

8 x 8 UDCT =20

8 x 8 UDCT =10

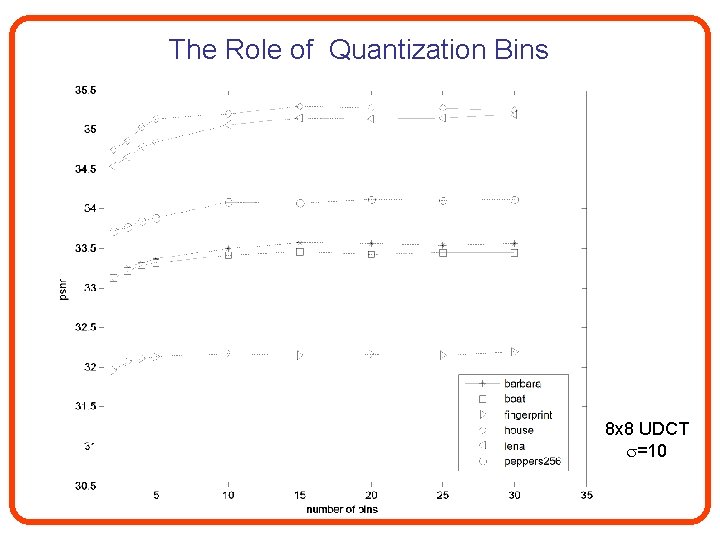
The Role of Quantization Bins 8 x 8 UDCT =10

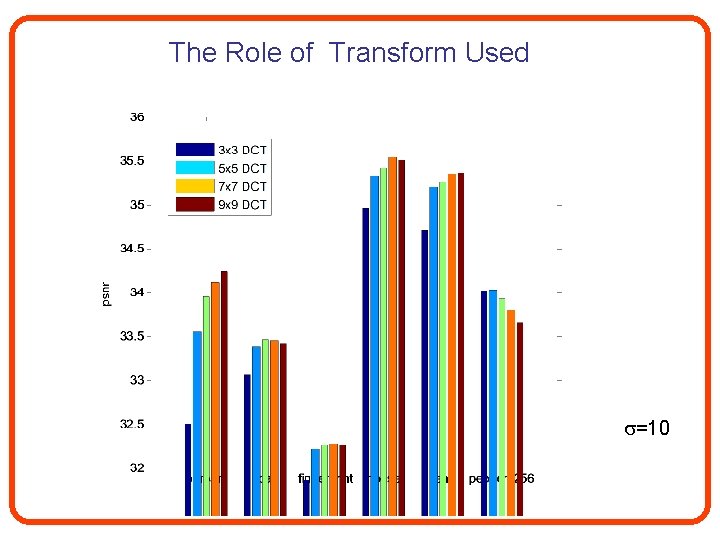
The Role of Transform Used =10

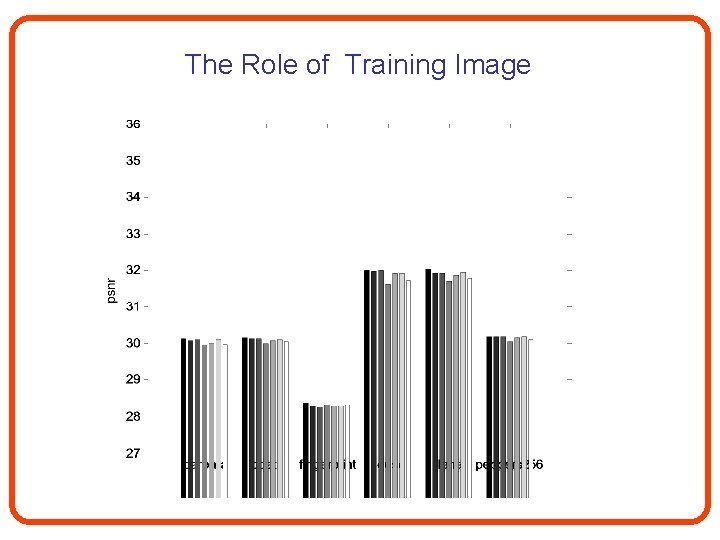
The Role of Training Image

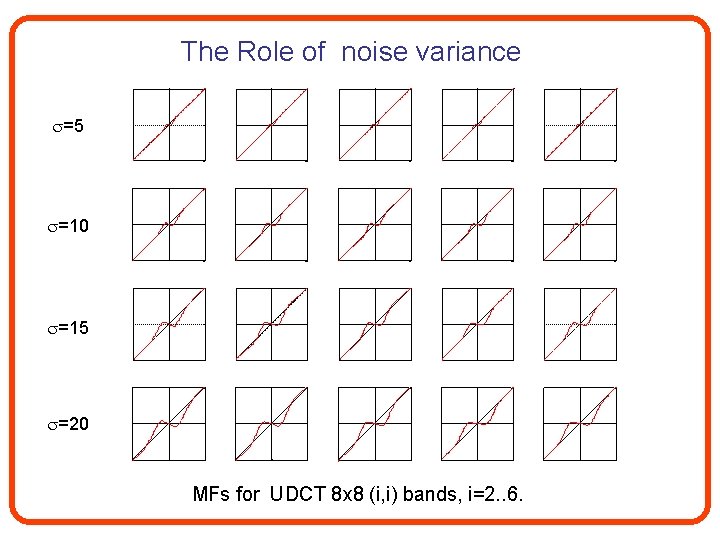
The Role of noise variance =5 =10 =15 =20 MFs for UDCT 8 x 8 (i, i) bands, i=2. . 6.

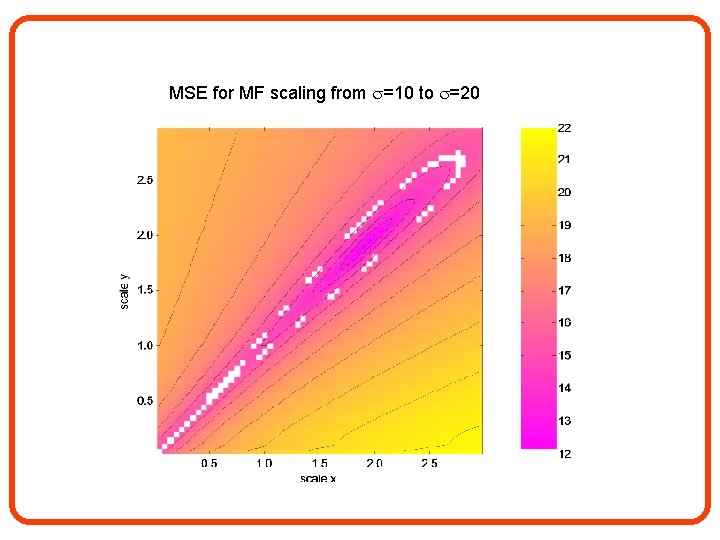
The role of noise variance • Observation: The obtained MFs for different noise variances are similar up to scaling:

Comparison between M 20(v) and 0. 5 M 10(2 v) for basis [2: 4]X[2: 4]

Comparison with BLS-GSM

Comparison with BLS-GSM

Other Degradation Models

JPEG Artifact Removal

JPEG Artifact Removal

Image Sharpening

Image Sharpening

Conclusions • New and simple scheme for over-complete transform based denoising. • MFs are optimized in a discriminative manner. • Linear formulation of non-linear minimization. • Eliminating the need for modeling complex statistical prior in high-dim. space. • Seamlessly applied to other degradation problems as long as scalar MFs are used for reconstruction.

Conclusions – cont. • Extensions: – Filter-cascade based denoising. – Multivariate MFs (activity level). – Non-homogeneous noise characteristics. • Open problems: – What is the best transform for a given image? – How to choose training images that form faithful representation?

Thank You

MSE for MF scaling from =10 to =20

MSE for MF scaling from =15 to =20

MSE for MF scaling from =25 to =20

Image Sharpening

Wavelet Shrinkage Pipe-line Wavelet transform B 1 B 1 Bi Shrinkage functions Inverse transform xi. B yi. B B 1 B 1 T B i (BTB)-1 +

Option 1 MFs for UDCT 8 x 8 (i, i) bands, i=1. . 4, =20

Option 2 MFs for UDCT 8 x 8 (i, i) bands, i=1. . 4, =20

Option 3 MFs for UDCT 8 x 8 (i, i) bands, i=1. . 4, =20

Comparing psnr results for 8 x 8 undecimated DCT, sigma=20.

Comparing psnr results for 8 x 8 undecimated DCT, sigma=10.