Discrimination and Classification Discrimination Situation We have two










![Proof: ECM = E[Cost of Misclassification] = c 2|1 P[1] P[2|1] + c 1|2 Proof: ECM = E[Cost of Misclassification] = c 2|1 P[1] P[2|1] + c 1|2](https://slidetodoc.com/presentation_image/01c9ef970231d2046c2312d019608b1d/image-11.jpg)



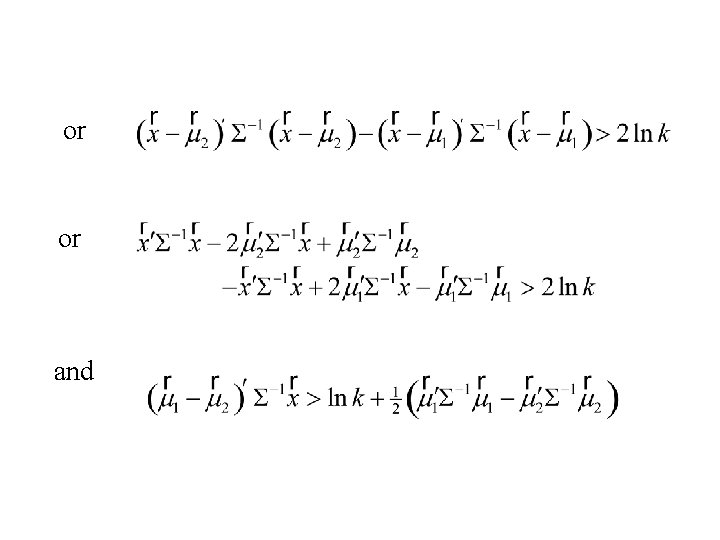





























- Slides: 45

Discrimination and Classification

Discrimination Situation: We have two or more populations p 1, p 2, etc (possibly p-variate normal). The populations are known (or we have data from each population) We have data for a new case (population unknown) and we want to identify the which population for which the new case is a member.

The Basic Problem Suppose that the data from a new case x 1, … , xp has joint density function either : p 1: g(x 1, … , xn) or p 2: h(x 1, … , xn) We want to make the decision to D 1: Classify the case in p 1 (g is the correct distribution) or D 2: Classify the case in p 2 (h is the correct distribution)

The Two Types of Errors 1. Misclassifying the case in p 1 when it actually lies in p 2. Let P[1|2] = P[D 1|p 2] = probability of this type of error 2. Misclassifying the case in p 2 when it actually lies in p 1. Let P[2|1] = P[D 2|p 1] = probability of this type of error This is similar Type I and Type II errors in hypothesis testing.

Note: A discrimination scheme is defined by splitting p – dimensional space into two regions. 1. C 1 = the region were we make the decision D 1. (the decision to classify the case in p 1) 2. C 2 = the region were we make the decision D 2. (the decision to classify the case in p 2)

There can be several approaches to determining the regions C 1 and C 2. All concerned with taking into account the probabilities of misclassification P[2|1] and P[1|2] 1. Set up the regions C 1 and C 2 so that one of the probabilities of misclassification , P[2|1] say, is at some low acceptable value a. Accept the level of the other probability of misclassification P[1|2] = b.

2. Set up the regions C 1 and C 2 so that the total probability of misclassification: P[Misclassification] = P[1] P[2|1] + P[2]P[1|2] is minimized P[1] = P[the case belongs to p 1] P[2] = P[the case belongs to p 2]

3. Set up the regions C 1 and C 2 so that the total expected cost of misclassification: E[Cost of Misclassification] = ECM = c 2|1 P[1] P[2|1] + c 1|2 P[2]P[1|2] is minimized P[1] = P[the case belongs to p 1] P[2] = P[the case belongs to p 2] c 2|1= the cost of misclassifying the case in p 2 when the case belongs to p 1. c 1|2= the cost of misclassifying the case in p 1 when the case belongs to p 2.

The Optimal Classification Rule Suppose that the data x 1, … , xp has joint density function f(x 1, … , xp ; q) where q is either q 1 or q 2. Let g(x 1, … , xp) = f(x 1, … , xn ; q 1) and h(x 1, … , xp) = f(x 1, … , xn ; q 2) We want to make the decision D 1: q = q 1 (g is the correct distribution) against D 2: q = q 2 (h is the correct distribution)

then the optimal regions (minimizing ECM, expected cost of misclassification) for making the decisions D 1 and D 2 respectively are C 1 and C 2 and where
![Proof ECM ECost of Misclassification c 21 P1 P21 c 12 Proof: ECM = E[Cost of Misclassification] = c 2|1 P[1] P[2|1] + c 1|2](https://slidetodoc.com/presentation_image/01c9ef970231d2046c2312d019608b1d/image-11.jpg)
Proof: ECM = E[Cost of Misclassification] = c 2|1 P[1] P[2|1] + c 1|2 P[2]P[1|2]

Therefore Thus ECM is minimized if C 1 contains all of the points (x 1, …, xp) such that the integrand is negative

Fishers Linear Discriminant Function. Suppose that x 1, … , xp is either data from a p-variate Normal distribution with mean vector: The covariance matrix S is the same for both populations p 1 and p 2.

The Neymann-Pearson Lemma states that we should classify into populations p 1 and p 2 using: That is make the decision D 1 : population is p 1 if l > k
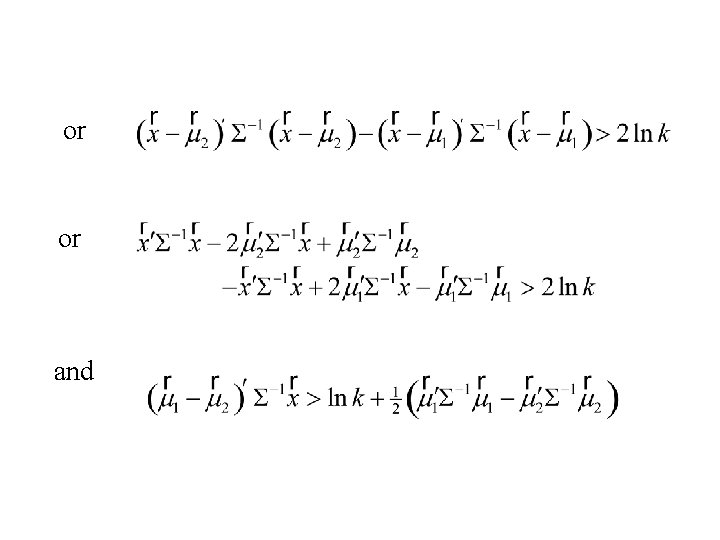
or or and

Finally we make the decision D 1 : population is p 1 if where and Note: k = 1 and ln k = 0 if c 1|2 = c 2|1 and P[1] = P[2].

The function Is called Fisher’s linear discriminant function

In the case where the populations are unknown but estimated from data Fisher’s linear discriminant function




Example 2 Annual financial data are collected for firms approximately 2 years prior to bankruptcy and for financially sound firms at about the same point in time. The data on the four variables • x 1 = CF/TD = (cash flow)/(total debt), • x 2 = NI/TA = (net income)/(Total assets), • x 3 = CA/CL = (current assets)/(current liabilties, and • x 4 = CA/NS = (current assets)/(net sales) are given in the following table.

The data are given in the following table:

Examples using SPSS

Classification or Cluster Analysis Have data from one or several populations

Situation • Have multivariate (or univariate) data from one or several populations (the number of populations is unknown) • Want to determine the number of populations and identify the populations

Example


Hierarchical Clustering Methods The following are the steps in the agglomerative Hierarchical clustering algorithm for grouping N objects (items or variables). 1. 2. 3. Start with N clusters, each consisting of a single entity and an N X N symmetric matrix (table) of distances (or similarities) D = (dij). Search the distance matrix for the nearest (most similar) pair of clusters. Let the distance between the "most similar" clusters U and V be d. UV. Merge clusters U and V. Label the newly formed cluster (UV). Update the entries in the distance matrix by a) b) deleting the rows and columns corresponding to clusters U and V and adding a row and column giving the distances between cluster (UV) and the remaining clusters.

4. Repeat steps 2 and 3 a total of N-1 times. (All objects will be a single cluster a termination of this algorithm. ) Record the identity of clusters that are merged and the levels (distances or similarities) at which the mergers take place.

Different methods of computing inter-cluster distance

Example To illustrate the single linkage algorithm, we consider the hypothetical distance matrix between pairs of five objects given below:

Treating each object as a cluster, the clustering begins by merging the two closest items (3 & 5). To implement the next level of clustering we need to compute the distances between cluster (35) and the remaining objects: d(35)1 = min{3, 11} = 3 d(35)2 = min{7, 10} = 7 d(35)4 = min{9, 8} = 8 The new distance matrix becomes:

The new distance matrix becomes: The next two closest clusters ((35) & 1) are merged to form cluster (135). Distances between this cluster and the remaining clusters become:

Distances between this cluster and the remaining clusters become: d(135)2 = min{7, 9} = 7 d(135)4 = min{8, 6} = 6 The distance matrix now becomes: Continuing the next two closest clusters (2 & 4) are merged to form cluster (24).

Distances between this cluster and the remaining clusters become: d(135)(24) = min{d(135)2, d(135)4)= min{7, 6} = 6 The final distance matrix now becomes: At the final step clusters (135) and (24) are merged to form the single cluster (12345) of all five items.

The results of this algorithm can be summarized graphically on the following "dendogram"

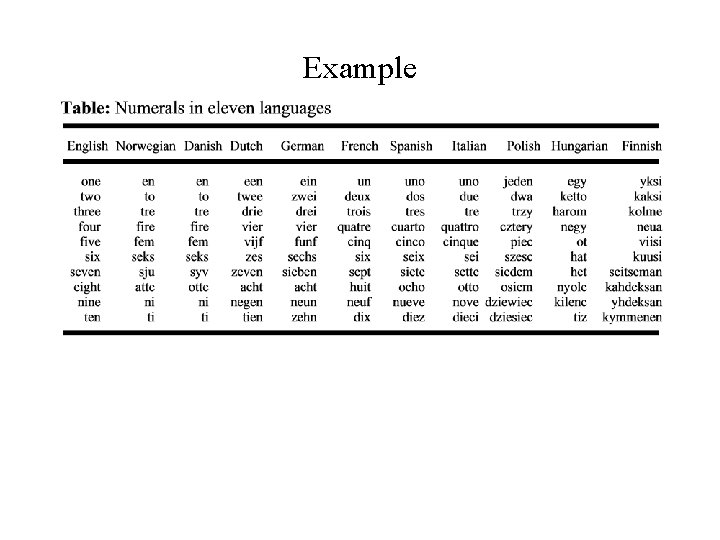
Dendograms for clustering the 11 languages on the basis of the ten numerals






Dendogram Cluster Analysis of N=22 Utility companies Euclidean distance, Average Linkage

Dendogram Cluster Analysis of N=22 Utility companies Euclidean distance, Single Linkage