DiscreteTime System Equations General Difference equation If we

Discrete-Time System Equations General Difference equation If we put n = n -N

Ex [n] = x [n + 1] E 2 x [n] = x [n + 2]. . . E N x [n] = x [n + N] For example y[n + 1] − ay[n] = x [n + 1] Ey[n] − ay[n] = E x[n] (E − a)y[n] = E x[n]

Q[E] y 0[n] = 0 The equation states that a linear combination of y 0 [n] and advanced y 0 [n] is zero not for some values of n but for all n. Such situation is possible if and only if y 0 [n] and advanced y 0 [n] have the same form. This is true only for an exponential function γ n+m = γ m γ n γn.

Therefore, if y 0[n] = cγ n we have Ey 0 [n] = y 0 [n + 1] = cγ n+1 = c γ γ n E 2 y 0 [n] = y 0 [n + 2] = cγ n+2 = c γ 2 γ n. . . EN y 0 [n] = y 0 [n + N] = cγ n+N = c γ N γ n System response to Internal Conditions: The Zero-Input Response cont. Substitution of these results to the system equation yields

The Unit Impulse Response h[n] Q[E] y[n] = P[E] x[n] The unit impulse response h[n] is the solution of this equation for the input δ[n] with all the initial conditions zero; that is Q[E] h[n] = P[E] δ[n] …. . (I) subject to initial conditions h[-1] = h[-2] = · · · = h[-n] = 0

The Unit Impulse Response h[n] •

The Unit Impulse Response h[n] •

The Unit Impulse Response h[n] •

The Unit Impulse Response h[n] •

Example Determine the unit impulse response h[n] for a system specified by the equation This equation can be expressed in the advance operator form as OR

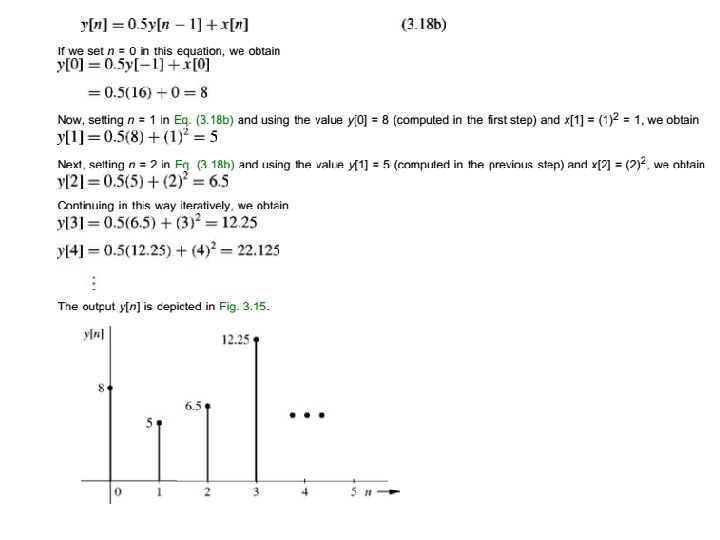
we have a. N = -0. 16 and b = 0. To determine c 1 and N c , we need to find two values of h[n] iteratively. 2

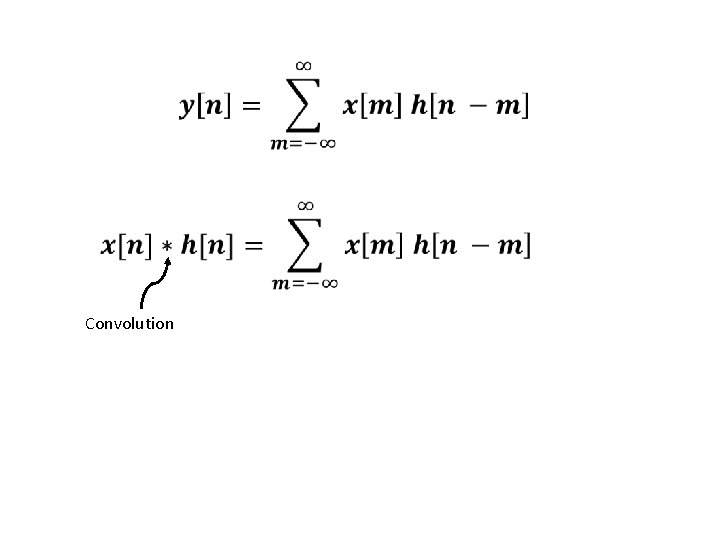
System Response to External Input The Zero-State Response • The zero-state response y[n] is the system response to an input x[n] when the system is in zero state. • Like in the continuous-time case an arbitrary input x[n] can be expressed as a sum of impulse components.

to indicate the input and the corresponding response of the system By using Linearity Property Again by using Linearity Property

Convolution

CAUSALITY AND ZERO-STATE RESPONSE • we assumed the system to be linear and time invariant. • In our applications, almost all the input signals are causal, and a majority of the systems are also causal. • If the input x[n] is causal, x[m] = 0 for m < 0. • if the system is causal (i. e. , if h[n] is causal), then h[x] = 0 for negative x, so that • h[n - m] = 0 when m > n • the product x[m]. h[n - m] = 0 for m < 0 and m > n, • it is nonzero only for the range 0 ≤ m ≤ n. •

Determine c[n] = x[n] ∗ g[n] for x[n] and g[n] both are causal because of u[n]

Using geometric progression with common ratio