Discretetime Sliding Mode Control S Janardhanan Sliding Mode

Discrete-time Sliding Mode Control S. Janardhanan

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Rethink: Quasi –Sliding mode n n Advantage : Is in discrete-time, more practical Disadvantage : n n Is Quasi. Not Exactly Sliding Mode There is always chattering. Even in theory.

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Why the chattering ? n QSMC is derived from ‘discretizing’ continuous SMC logic. n The signum term is required in CSMC

Sliding Mode Lectures : Lecture 12 : DSMC Chattering. . Why ? n In discrete-time system n n n The sign(s) changes abruptly near s=0 Control cannot be changed at any time Result : Always chattering S. Janardhanan

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Fresh Approach n n Let us again see the aim of sliding mode control. But, now in discrete-time systems Aim : To get the system to the sliding surface and maintain the state on the surface n n To get to the surface : s(k+1)=0 (with s(k) 0) To maintain : Again s(k+1)=0

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Discrete-time sliding mode n n So, apparently the reaching law is simply s(k+1)=0 For this the control would be

Sliding Mode Lectures : Lecture 12 : DSMC Problem n The control action n Problem n n Brings the system to sliding mode in one step Keeps RP on sliding surface thereafter. Probability of too much control in the ‘one step’ Solution n n GO SLOW But, be sure you are going forward S. Janardhanan

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Mathematically speaking … n n Let the maximum applicable control be u 0 Use the control as

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan To go in right direction n n The control u 1 tries to make s(k+1)=0 But, it may require too much ‘effort’. So, with limited resources we can apply a maximum of only u 0. Now, to be sure this is ‘enough’. Ie. , we are moving forward, we get the condition

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan The condition n Thus, the condition for this logic to work is See : G. Bartolini, A. Ferrara and V. Utkin, “Adaptive sliding mode control in discrete-time systems”, Automatica, Vol. 31, No. 5, pp. 769 -773, May 1995.

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Extension to Uncertain Systems n n The same algorithm can be extended to systems with matched uncertainty. In this case, the condition would become

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Another Algorithm n n Another approach to the DSMC problem is to design a control algorithm that would inherently ‘go slow’. Instead of trying to reach the surface in one step. Try to reach it in say k* steps.

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan The Problem Statement n Consider the design of DSMC for system c. Tx=s(k) is the desired sliding surface n Bartoszewicz proposed the reaching law See : A. Bartoszewicz, “Discrete-time quasi-sliding mode control strategies”, IEEE Trans. Ind. Electron. , Vo. 45, No. 1, pp. 633 -637, 1998

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Bartoszewicz QSMC … n sd is an a priori known function such that sd(k) is always of the same sign

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Feasible Sd(k) n A feasible function for sd(k) that satisfies the above said conditions can be given as

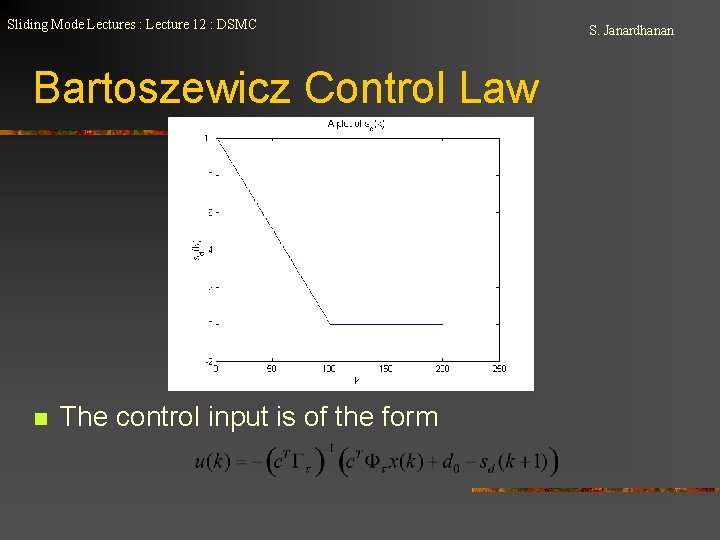
Sliding Mode Lectures : Lecture 12 : DSMC Bartoszewicz Control Law n The control input is of the form S. Janardhanan

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Proof of Convergence n The Bartoszewicz control law satisfies the reaching condition n For n hence and to s(k)=0 in deterministic systems atleast in theory.

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Proposed Algorithm n n Combines Bartoszewicz’s approach and FOS to get multirate output feedback based QSMC control strategy that does not have switching function and hence no chatter. Reaching Law Modified

Sliding Mode Lectures : Lecture 12 : DSMC Proposed Control Law n The Control is of the form S. Janardhanan

Sliding Mode Lectures : Lecture 12 : DSMC S. Janardhanan Proof of Convergence n The proposed control law satisfies the reaching condition n For n Hence and to s(k)=0 in deterministic systems atleast in theory.