Discrete Structures Discrete Mathematics Amanullah Kariapper Email amanullah




































- Slides: 47

Discrete Structures (Discrete Mathematics) Amanullah Kariapper Email: amanullah. jiffrey@ucp. edu. pk

Discrete World: • What is Discrete Mathematics? • Adjective: Individually separate and distinct. • Synonyms: separate - detached - distinct - abstract.

Discrete World: • What is Discrete Mathematics? • Adjective: Individually separate and distinct. • Synonyms: separate - detached - distinct - abstract. • What is mathematics? The study of numbers? In part, but you also study functions and lines and triangles and parallelepipeds and vectors and …. Or perhaps you want to say that mathematics is a collection of tools that allow you to solve problems. What sort of problems? Okay, those that involve numbers, functions, lines, triangles, …. Whatever your conception of what mathematics is, try applying the concept of “discrete” to it, as defined above. Some math fundamentally deals with stuff that is individually separate and distinct.

The Problems we solve: • One way to get a feel for the subject is to consider the types of problems you solve in discrete math. Here a few simple examples:

The Problems we solve: Counting possible passwords Each user on a computer system has a password, which is six to eight characters long, where each character is an uppercase letter or a digit. Each password must contain at least one digit. How many possible passwords are there?

The Problems we solve: Counting possible passwords Each user on a computer system has a password, which is six to eight characters long, where each character is a letter or a digit. Each password must contain at least ONE DIGIT, ONE UPPER CASE and ONE LOWER CASE letter. How many possible passwords are there?

Examples – The Problems we solve: The most popular mathematician in the world is throwing a party for all of his friends. As a way to kick things off, they decide that everyone should shake hands. Assuming all 10 people at the party each shake hands with every other person (but not themselves, obviously) exactly once, how many handshakes take place?

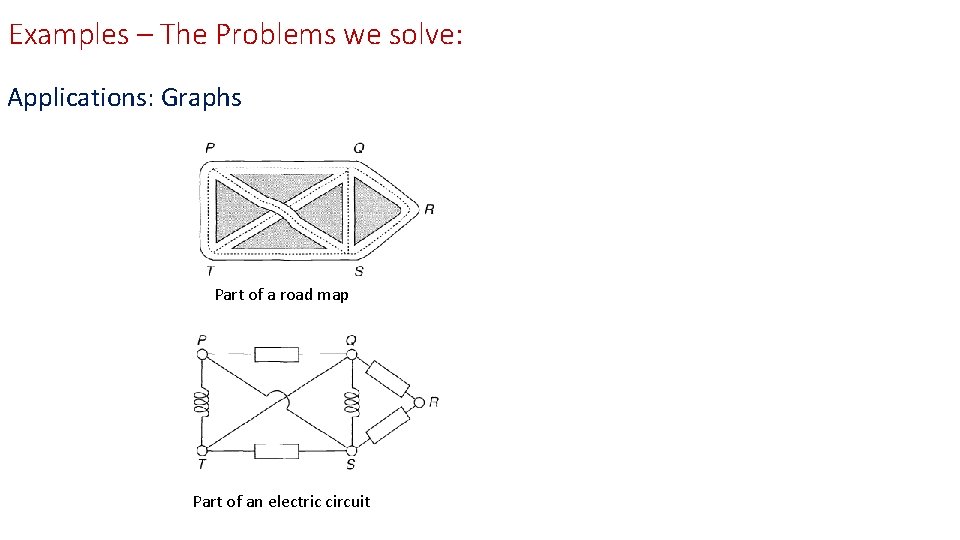
Examples – The Problems we solve: Applications: Graphs Part of a road map Part of an electric circuit

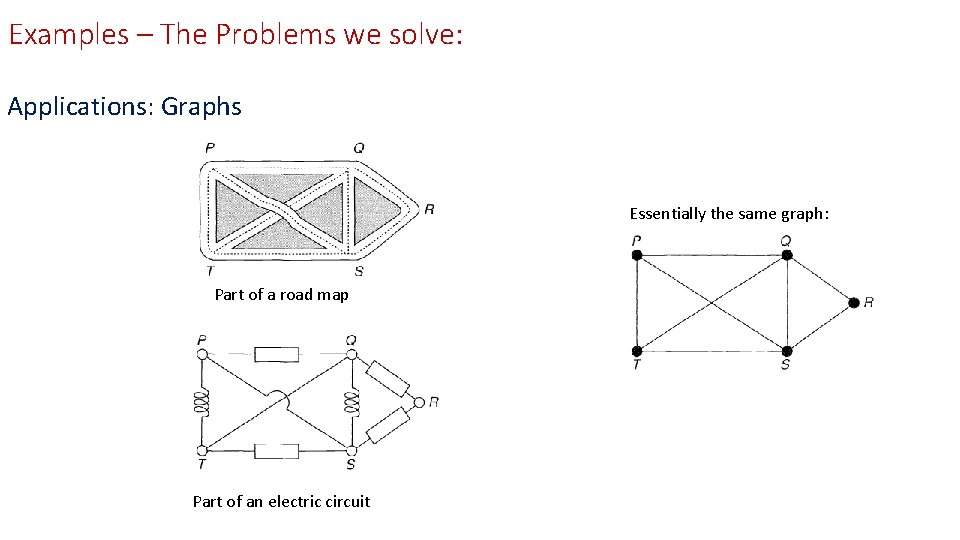
Examples – The Problems we solve: Applications: Graphs Essentially the same graph: Part of a road map Part of an electric circuit

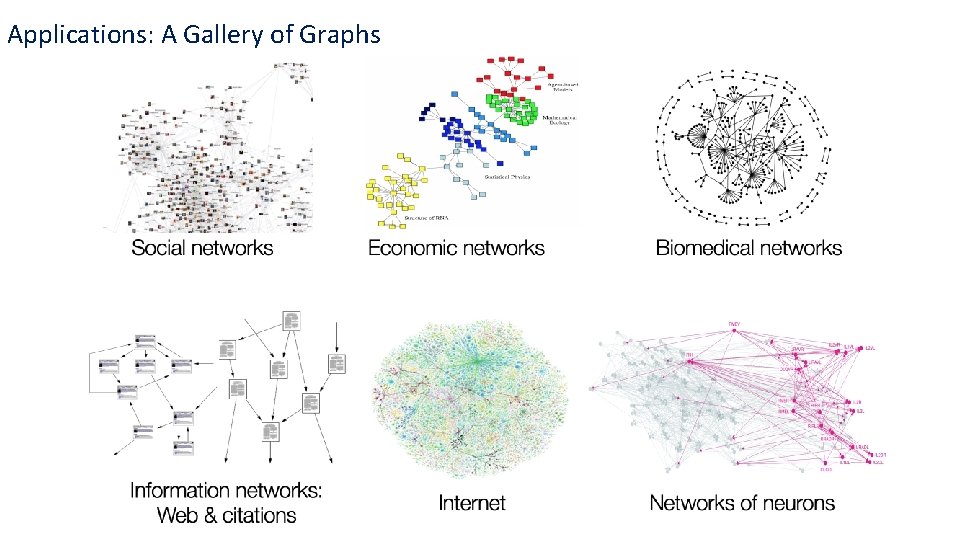
Applications: A Gallery of Graphs

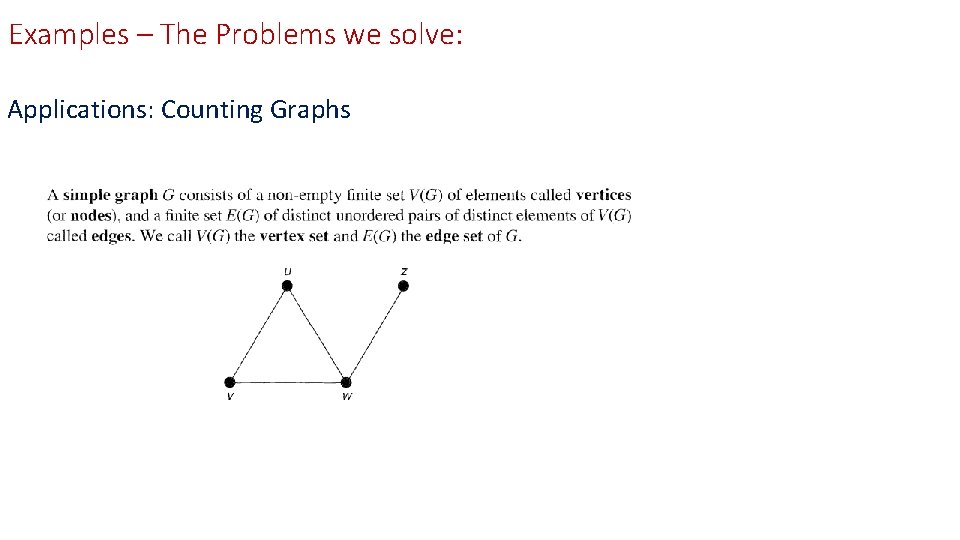
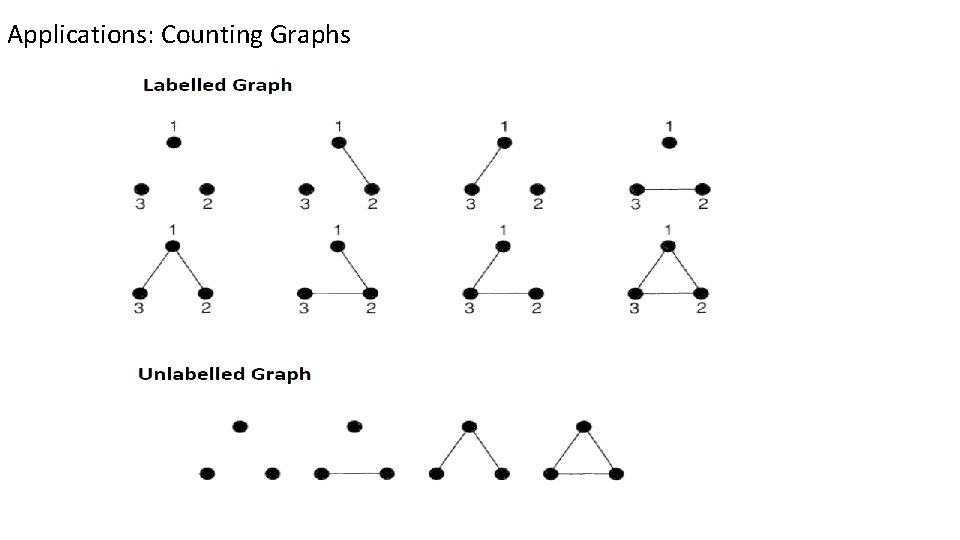
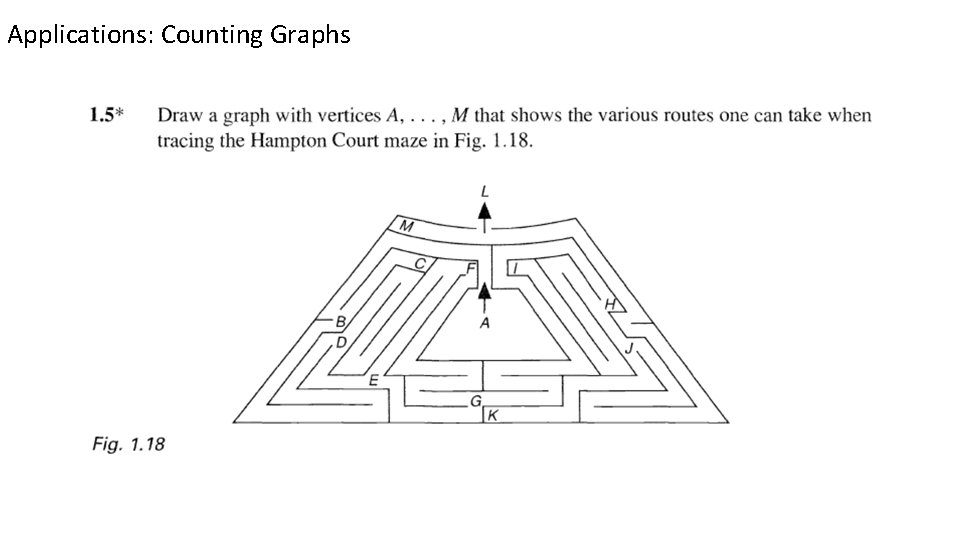
Examples – The Problems we solve: Applications: Counting Graphs

Examples – The Problems we solve: Applications: Counting Graphs

Applications: Counting Graphs

Applications: Counting Graphs

Examples – The Problems we solve: Bijections (or the art of noticing equivalences) The three Guddoo siblings, Ali, Bilal, and Camaal, have integer ages that sum to 15. How many possible distributions of ages are there? Note: It is possible that an age can be 0, which means that the child was just born.

Bijections (or the art of noticing equivalences) •

Bijections (or the art of noticing equivalences) The three Gudoo siblings, Ali, Bilal, and Camaal, have integer ages that sum to 15. How many possible distributions of ages are there? Note: It is possible that an age can be 0, which means that the child was just born. One can establish a bijection between the set of distributions of ages and a set of combinations. Consider the arrangement of stars and bars below: ⋆⋆∣⋆⋆⋆⋆⋆⋆⋆⋆⋆ This arrangement corresponds to the following distribution of ages: Ali - 2, Bilal - 4, Camaal - 9. How many ways to place the 2 bars among the 15 stars?

Bijections (or the art of noticing equivalences)

Examples – The Problems we solve: In the world of Indiana Jones,

Examples – The Problems we solve: Proofs •

Examples – The Problems we solve: Proofs •

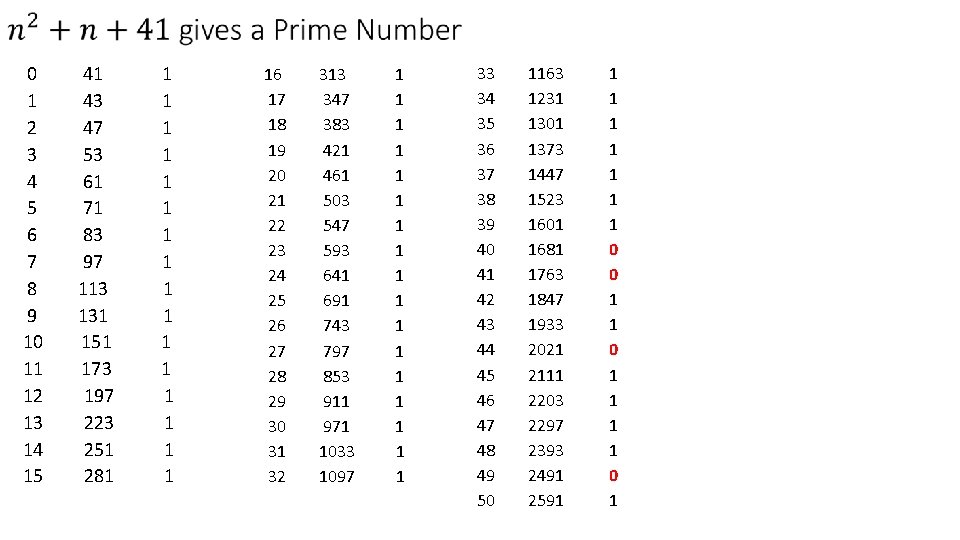
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 41 43 47 53 61 71 83 97 113 131 151 173 197 223 251 281 1 1 1 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 313 347 383 421 461 503 547 593 641 691 743 797 853 911 971 1033 1097 1 1 1 1 1 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 1163 1231 1301 1373 1447 1523 1601 1681 1763 1847 1933 2021 2111 2203 2297 2393 2491 2591 1 1 1 0 0 1 1 1 1 0 1

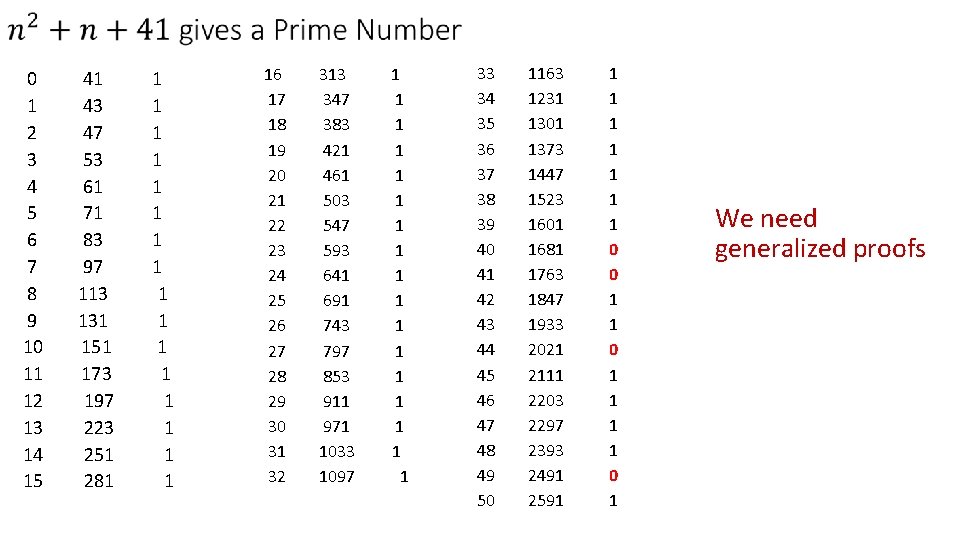
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 41 43 47 53 61 71 83 97 113 131 151 173 197 223 251 281 1 1 1 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 313 347 383 421 461 503 547 593 641 691 743 797 853 911 971 1033 1097 1 1 1 1 1 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 1163 1231 1301 1373 1447 1523 1601 1681 1763 1847 1933 2021 2111 2203 2297 2393 2491 2591 1 1 1 0 0 1 1 1 1 0 1 We need generalized proofs


What’s wrong in this Proof ? ? ?

At times, we think in a non-conventional way

At times, we think in a non-conventional way Please watch: https: //www. youtube. com/watch? v=jc. KRGp. Mi. VTw

At times, we think in a non-conventional way Do watch: Genius of Ramanujan: https: //www. youtube. com/watch? v=f. GFK 7 rhpb. Wk&t=74 s

Always think rational, think imaginative, think out of the box What is color of the bear A bear starting from point P, walked one mile due south, then he changed direction and walked one mile due east, then he turned again and walked one mile due north, and arrived exactly at the point P where he started from. What color is the bear?

Always think rational, think imaginative, think out of the box

A Computer Scientist is a person who can construct algorithms based on conjectures he/she can prove.

A Computer Scientist is a person who can construct algorithms based on conjectures he/she can prove. Algorithms: Efficient and Correct How do we approach: Solve a Problem Construct an Algorithm Develop Code

• A Computer Scientist is a person who can construct algorithms based on conjectures he/she can prove. Algorithms: Efficient and Correct How do we approach: Solve a Problem (proofs – problem solving – Discrete Maths) Construct an Algorithm (Analysis of Algorithms – Data Structures) Develop Code (All other relevant skills)

A Computer Scientist is a person who can construct algorithms based on conjectures he/she can prove. Algorithms: Efficient and Correct How do we approach: Solve a Problem (proofs – problem solving – Discrete Maths) Construct an Algorithm (Analysis of Algorithms – Data Structures) Develop Code (All other relevant skills) A GOOD PROOF: Existence of a book where God writes nice proofs for al mathematical results.

Course Outlines: 1: Counting a. b. c. d. e. f. Sets Graphs Functions Relations Combinations and Permutations Tools: Induction, Pigeonhole principle, Principle of inclusion-exclusion MIDTERM 2: Logic and Proofs a. Propositional logic b. Basic techniques of proofs c. Mathematical induction FINAL

Course Outlines: Assessments: • Assignments (25%) • – Each assignment is worth 2. 5% • - Weekly assignment, issued on every Tuesday, submit on next Wednesday • Quizzes (15 %) • Paper based short-quizzes in class, (during 1 st 10 min of class – don’t be late) • Project/Report (5%) • Writing paper on a discrete mathematics problem (we shall provide you list of problems, after mid-term. You have to choose one and work on it) • Mid Term Exam (20%) • Final Exam (35%) • Comprehensive Final Exam

Textbook: • Main Text: • K. Rosen: Discrete Structures and its Applications • Weekly Readings: • L. Lovasz: Discrete Mathematics, Elementary and Beyond • Reference: • R. J. Wilson: Graph Theory

Therefore O students, study mathematics and do not build without foundations - Leonardo da Vinci (1452 -1519)

Therefore O students, study mathematics and do not build without foundations - Leonardo da Vinci (1452 -1519) - Go through the reading material: Lovasz’s book – Chapter 1, Section 1. 1 – 1. 2

Therefore O students, study mathematics and do not build without foundations - Leonardo da Vinci (1452 -1519) - My office: Centre For Game Design, R-205, B-Building Email: amanullah. jiffrey@ucp. edu. pk Office Hours: Monday: 14: 30 – 15: 30 Wednesday : 14: 30 – 15: 30 or by appointment (email)

Good Practices • Be on time in class • Be regular (do not miss a single class) • Start assignments on time • Do not miss any assignment or quiz • Come up with good questions (ask in class/after class) • Visit during office hours to discuss problems/assignments your

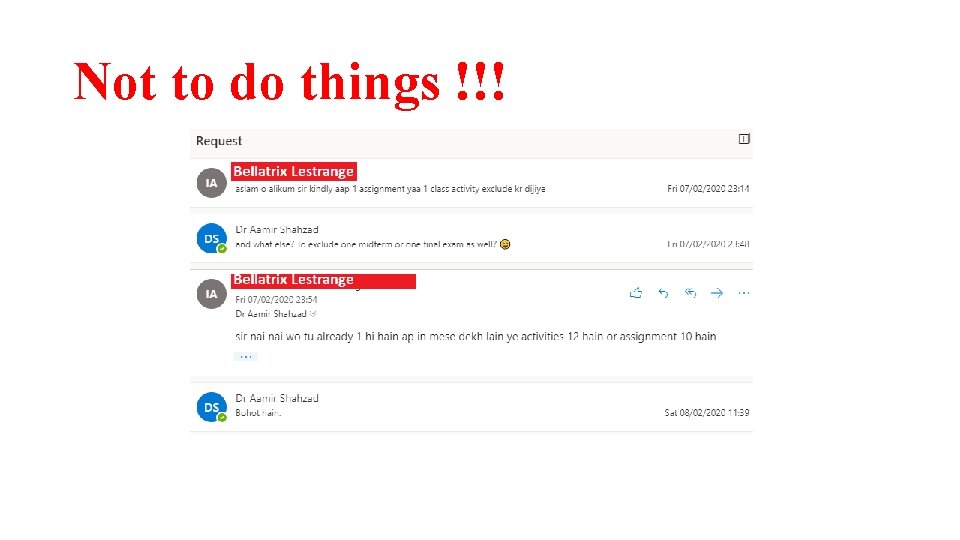
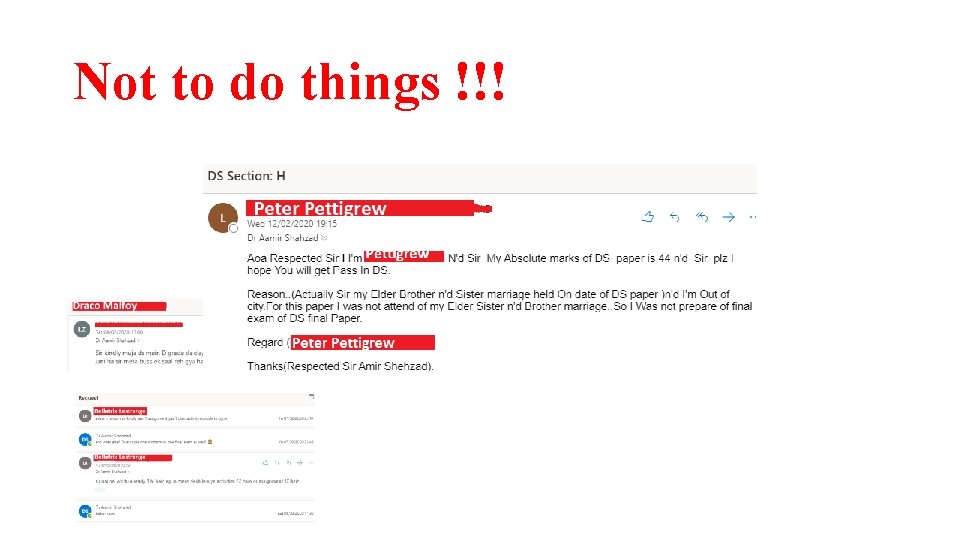
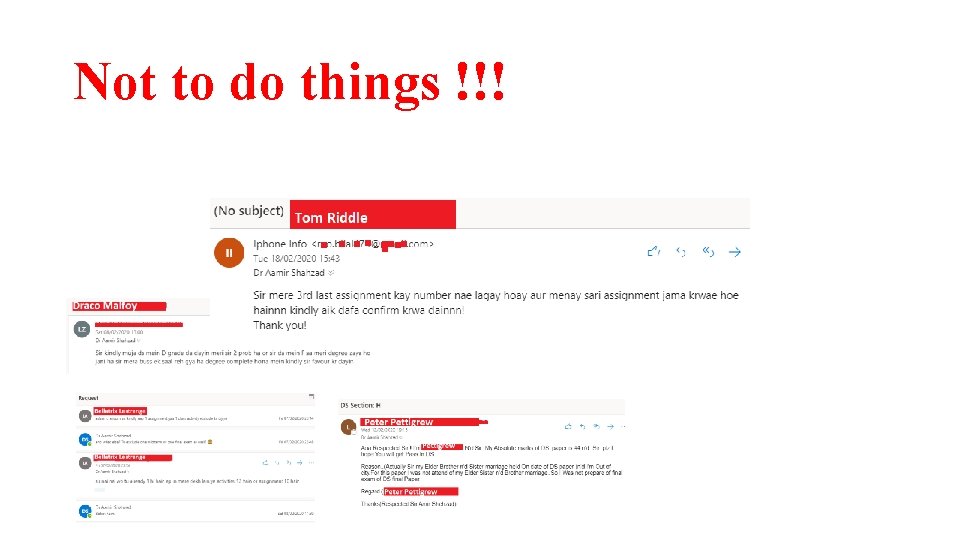
Bad Practices • Excuses • Coming late in class (remember: quiz will be in 1 st 10 min of class) • Come to class without pen and notebooks • Asking for leaves --- Teacher has no authority to grant leaves. Manage your 6 absents as emergency leaves, or request Ho. D/Dean for extra leaves. • Requesting to increase marks • Coming to class without reading the required text/notes • Copying / plagiarism • Asking to extend the deadline

Not to do things !!!

Not to do things !!!

Not to do things !!!

Not to do things !!!

Therefore O students, study mathematics and do not build without foundations - Leonardo da Vinci (1452 -1519) - My office: Centre For Game Design, R-205, B-Building Thank you …!!!