Discrete Structures CSC 102 Lecture 31 Graphs and

Discrete Structures (CSC 102) Lecture 31

Graphs and Trees

Previous Lecture v Euler Circuits v Finding an Euler Circuit v Euler Trails v Finding an Euler Trail v Hamiltonian Circuits v A Traveling Salesman Problem

Today’s Lecture v Matrices and Graphs v Matrices and Directed Graphs v Matrices and undirected Graphs v Matrices and Connected Components v Trees v Characterizing Trees v Rooted Trees

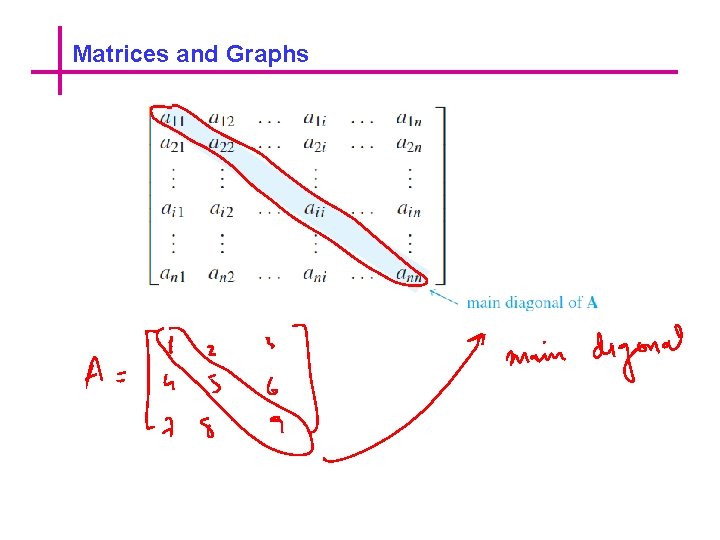
Matrices and Graphs How can graphs be represented inside a computer? It happens that all the information needed to specify a graph can be conveyed by a structure called a matrix, and matrices are easy to represent inside computers.

Matrices and Graphs The entry ai j in the ith row and j th column of A is called the ijth entry of A. An m × n matrix is said to have size m × n. If A and B are matrices, then A = B if, and only if, A and B have the same size and the corresponding entries of A and B are all equal; that is, ai j = bi j for all i = 1, 2, . . . , m and j = 1, 2. . . , n. A matrix for which the numbers of rows and columns are equal is called a square matrix. If A is a square matrix of size n × n, then the main diagonal of A consists of all the entries a 11, a 22, . . . , ann

Matrices and Graphs

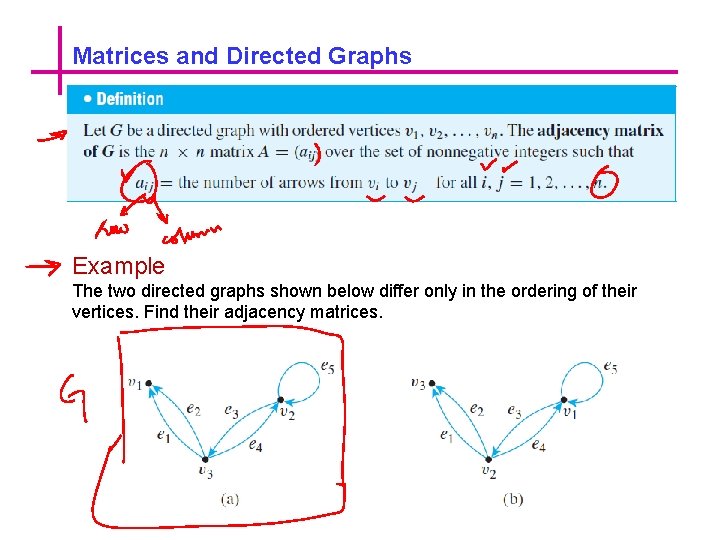
Matrices and Directed Graphs Example The two directed graphs shown below differ only in the ordering of their vertices. Find their adjacency matrices.

The Adjacency Matrix of a Graph Since both graphs have three vertices, both adjacency matrices are 3 × 3 matrices. For (a), all entries in the first row are 0 since there are no arrows from v 1 to any other vertex. For (b), the first two entries in the first row are 1 and the third entry is 0 since from v 1 there are single arrows to v 1 and to v 2 and no arrows to v 3. Continuing the analysis in this way, you obtain the following two adjacency matrices.

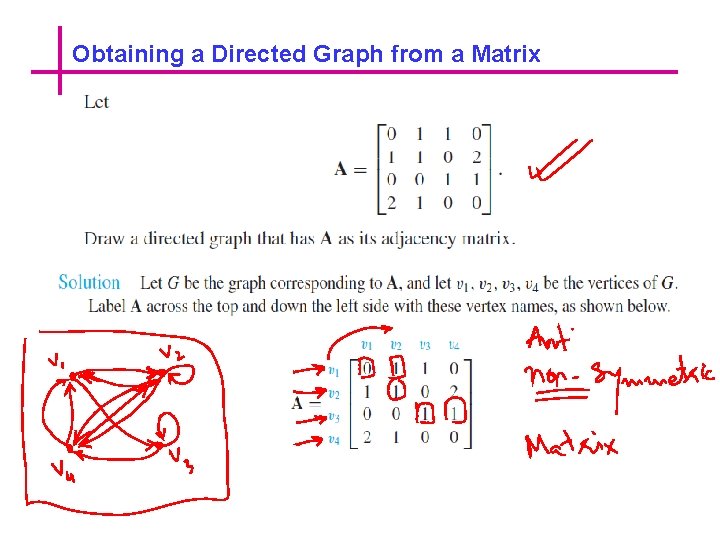
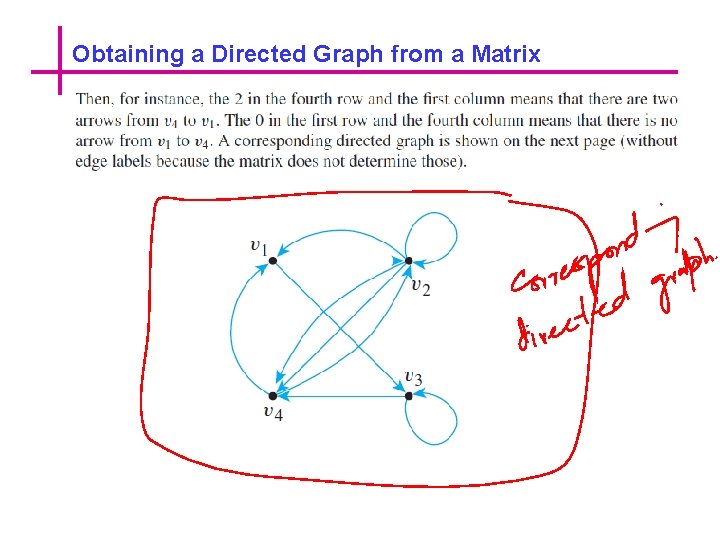
Obtaining a Directed Graph from a Matrix

Obtaining a Directed Graph from a Matrix

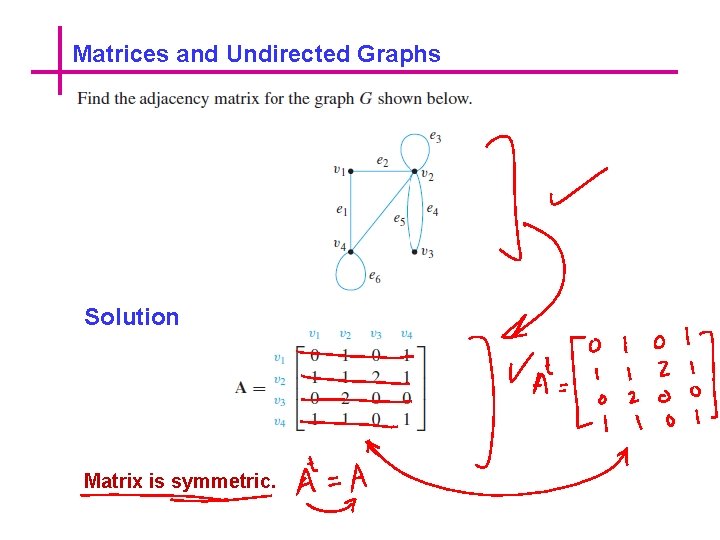
Matrices and Undirected Graphs

Matrices and Undirected Graphs Solution Matrix is symmetric.

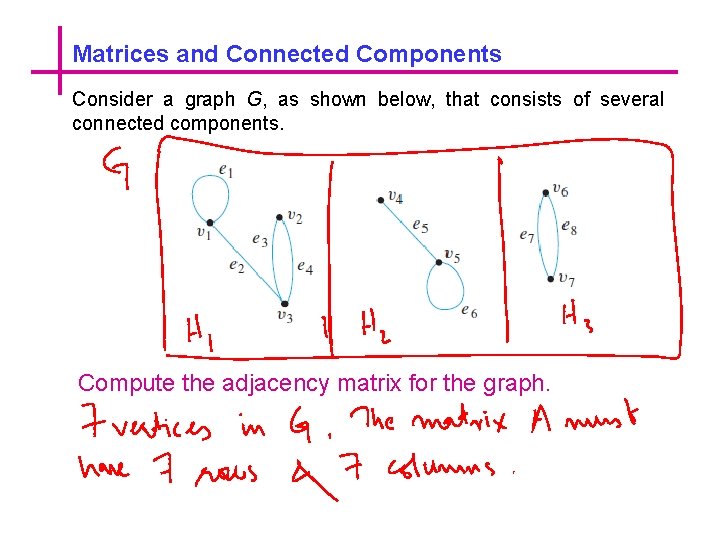
Matrices and Connected Components Consider a graph G, as shown below, that consists of several connected components. Compute the adjacency matrix for the graph.

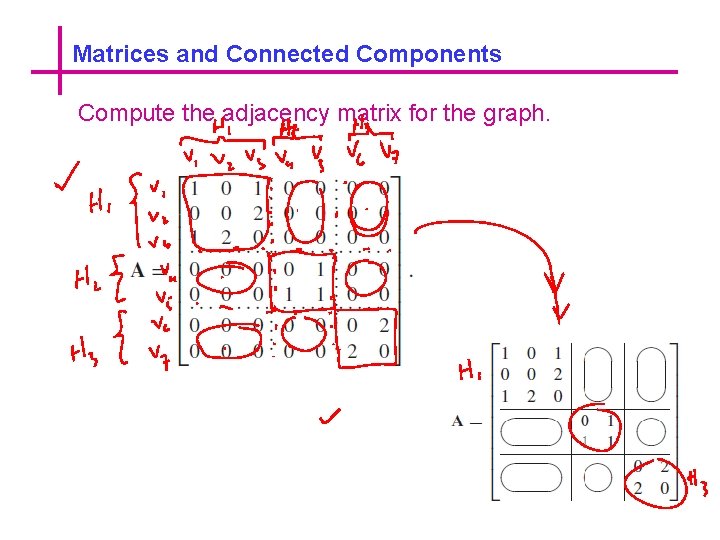
Matrices and Connected Components Compute the adjacency matrix for the graph.

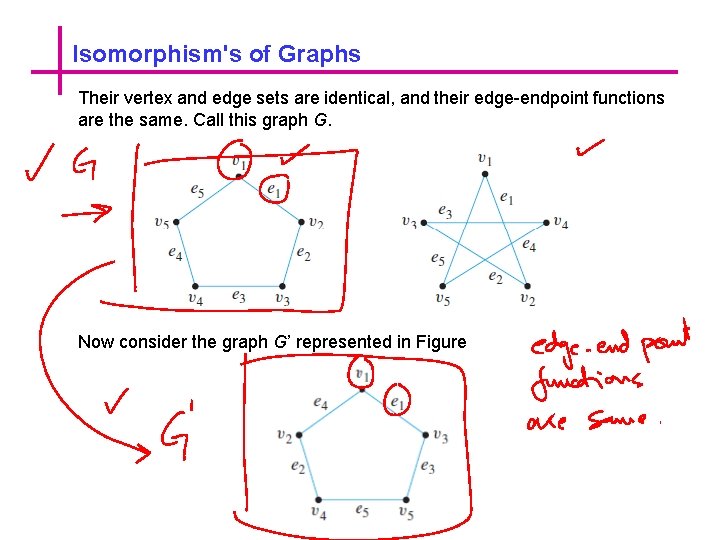
Isomorphism's of Graphs Their vertex and edge sets are identical, and their edge-endpoint functions are the same. Call this graph G. Now consider the graph G’ represented in Figure

Isomorphism's of Graphs Observe that G’ is a different graph from G (for instance, in G the endpoints of e 1 are v 1 and v 2 , whereas in G’ the endpoints of e 1 are v 1 and v 3). Yet G’ is certainly very similar to G. In fact, if the vertices and edges of G’ are relabeled, then G’ becomes the same as G. Note that these relabeling functions are one-to-one and onto. Two graphs that are the same except for the labeling of their vertices and edges are called isomorphic. The word isomorphism comes from the Greek, meaning “same form. ” Isomorphic graphs are those that have essentially the same form.

Isomorphism's of Graphs

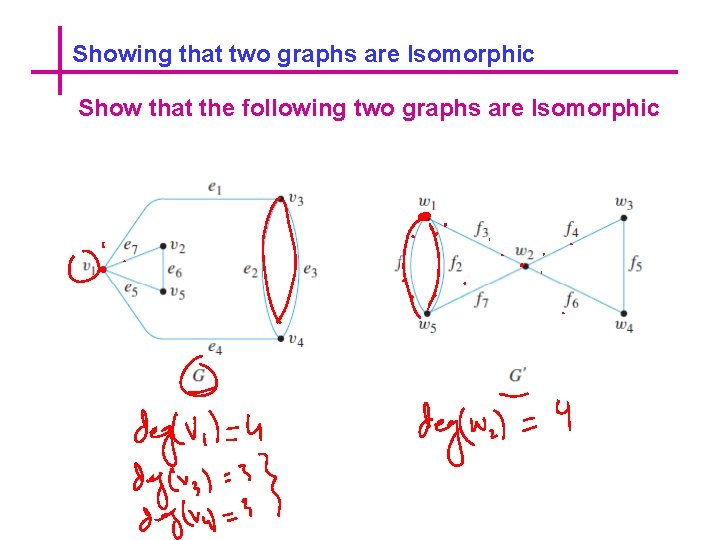
Showing that two graphs are Isomorphic Show that the following two graphs are Isomorphic

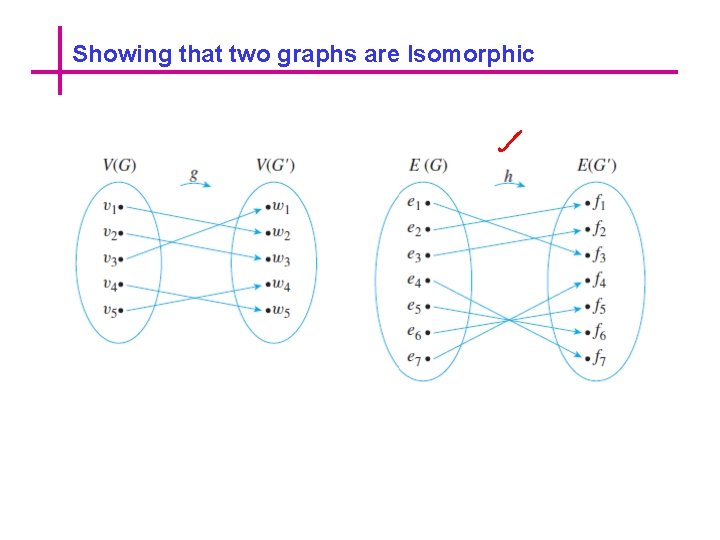
Showing that two graphs are Isomorphic

Showing that two graphs are Isomorphic

Invariant Property Theorem

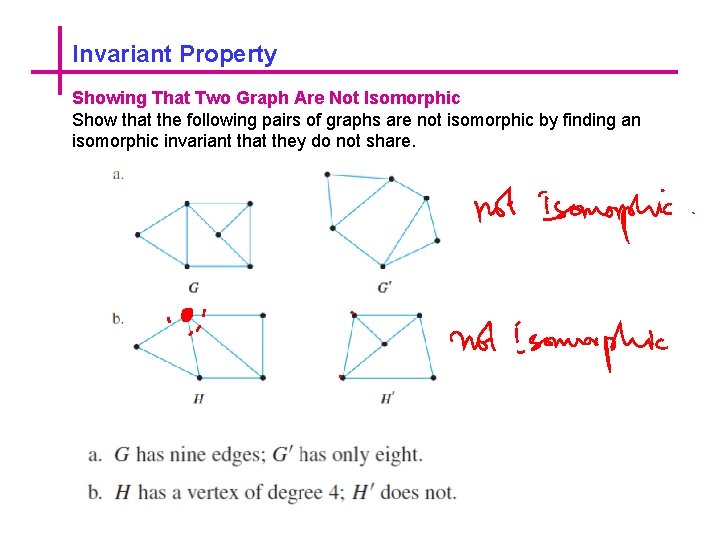
Invariant Property Showing That Two Graph Are Not Isomorphic Show that the following pairs of graphs are not isomorphic by finding an isomorphic invariant that they do not share.

Trees

Trees and Non Trees

Trees and Non Trees

Examples of Trees A Decision Tree During orientation week, a college administers an exam to all entering students to determine placement in the mathematics curriculum. The exam consists of two parts, and placement recommendations are made as indicated by the tree shown in figure. Read the tree from left to right to decide what course should be recommended for a student who scored 9 on part I and 7 on part II.

Characterizing Trees Theorems • Any tree that has more than one vertex has at least one vertex of degree 1. • For any positive integer n, any tree with n vertices has n − 1 edges. • For any positive integer n, if G is a connected graph with n vertices and n − 1 edges, then G is a tree.

Characterizing Trees Example Find all terminal vertices and all internal vertices in the following tree: The terminal vertices are v 0, v 2, v 4, v 5, v 7, and v 8. The internal vertices are v 6, v 1, and v 3.

Characterizing Trees Example A graph G has ten vertices and twelve edges. Is it a tree? No. By Theorem, any tree with ten vertices has nine edges, not twelve. Example A Graph with n Vertices and n − 1 Edges That Is Not a Tree. By Theorem, such a graph cannot be connected. One example of such an unconnected graph is shown below.

Rooted Trees

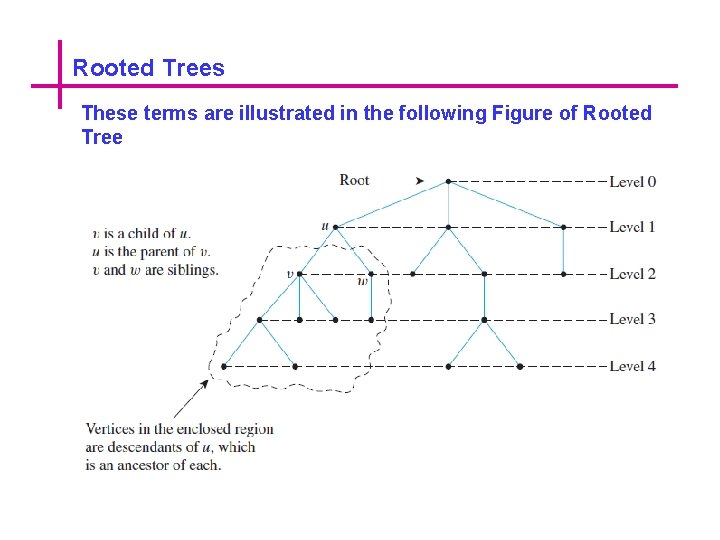
Rooted Trees These terms are illustrated in the following Figure of Rooted Tree

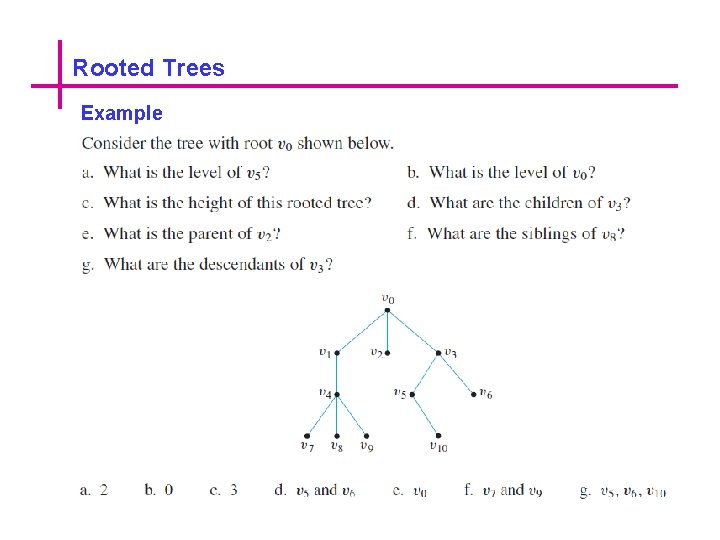
Rooted Trees Example

Binary Trees

Representation of Algebraic Expressions a/b ((a − b)·c) + (d/e) a/(c+d)

Lecture Summary v Subgraphs v The Concept of Degree v Walks, Trails, Paths and Circuits v Connectedness v Connected Component of a Graph v Euler Circuits v Finding an Euler Circuit