Discrete Structures CSC 102 Lecture 26 Counting Rules

Discrete Structures (CSC 102) Lecture 26

Counting Rules II

Previous Lecture v Introduction v Multiplication Rule v Permutations of Objects Around a Circle v Property of P(n, r)

Today Lecture v Counting Elements v Difference Rule v Inclusion/Exclusion Rule v Pigeon Hole Principle v Generalized Pigeon Hole Principle

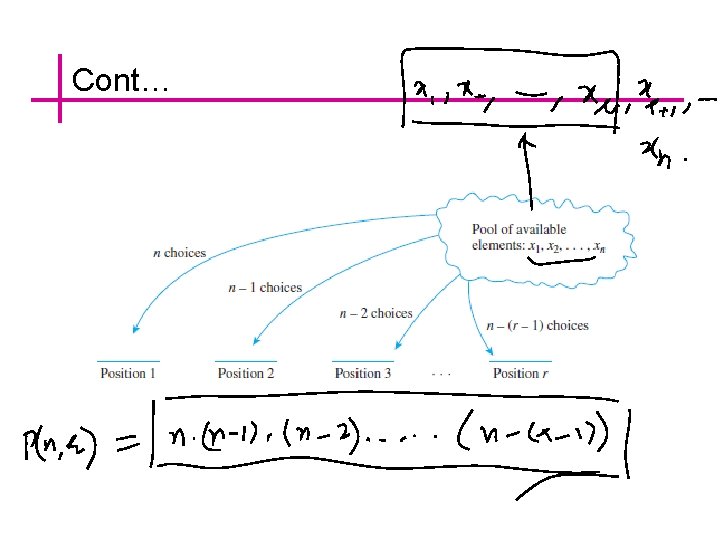
Permutations A permutation of a set of objects is an ordering of the objects in a row. For example, the set of elements a, b, and c has six permutations. abc, acb, cba, bac, bca, cab In general, given a set of n objects, how many permutations does the set have? Imagine forming a permutation as an n-step operation:

Cont…

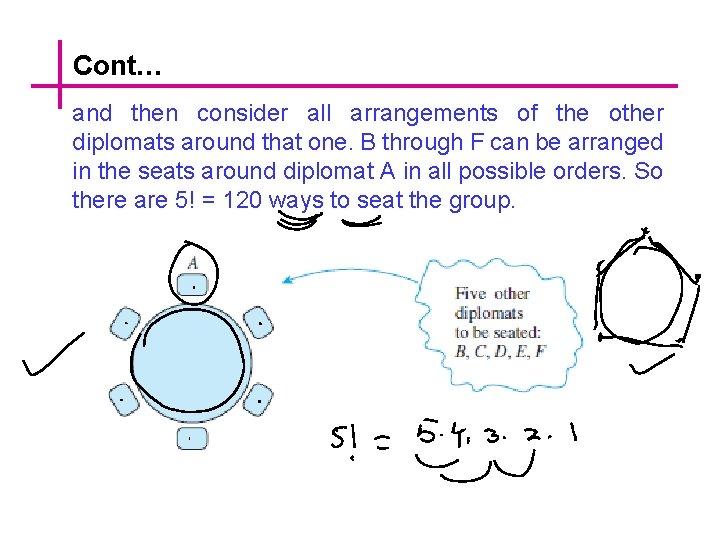
Permutations of Objects Around a Circle At a meeting of diplomats, the six participants are to be seated around a circular table. Since the table has no ends to confer particular status, it doesn’t matter who sits in which chair. But it does matter how the diplomats are seated relative to each other. In other words, two seating's are considered the same if one is a rotation of the other. How many different ways can the diplomats be seated? Solution: Call the diplomats by the letters A, B, C, D, E, and F. Since only relative position matters, you can start with any diplomat (say A), place that diplomat anywhere

Cont… and then consider all arrangements of the other diplomats around that one. B through F can be arranged in the seats around diplomat A in all possible orders. So there are 5! = 120 ways to seat the group.

Permutations of Selected Elements

Cont…

Evaluating r-Permutations a. Evaluate P(5, 2). b. How many 4 -permutations are there of a set of seven objects? c. How many 5 -permutations are there of a set of five objects?

Permutations of Selected Letters of a Word a. How many different ways can three of the letters of the word BYTES be chosen and written in a row? b. How many different ways can this be done if the first letter must be B?

Cont…

Proving a Property of P(n, r) Prove that for all integers n ≥ 2, P(n, 2) + P(n, 1) = n 2

Counting Elements of Disjoint Sets: For example: A computer access password consists of from one to three letters chosen from the 26 in the alphabet with repetitions allowed. How many different passwords are possible? Sol: The set of all passwords can be partitioned into subsets consisting of those of length 1, those of length 2, and those of length 3 as shown in Figure

Cont…

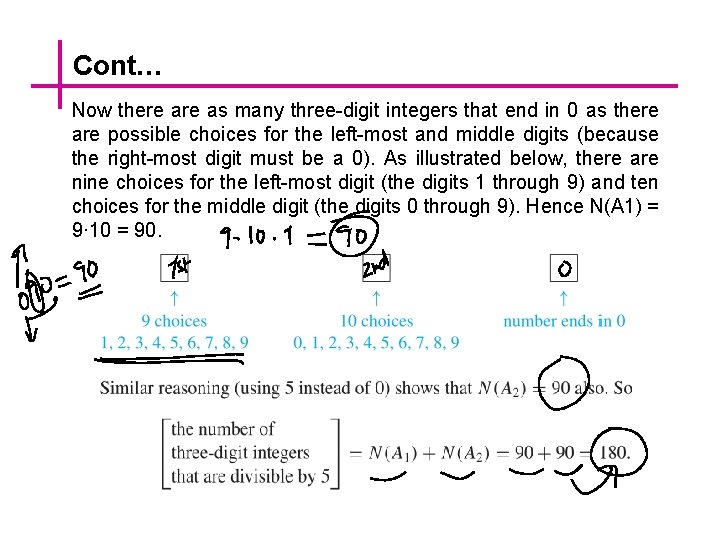
Counting the Number of Integers How many three-digit integers (integers from 100 to 999 inclusive) are divisible by 5? Solution: Integers that are divisible by 5 end either in 5 or in 0. Thus the set of all three-digit integers that are divisible by 5 can be split into two mutually disjoint subsets A 1 and A 2 as shown in Figure

Cont… Now there as many three-digit integers that end in 0 as there are possible choices for the left-most and middle digits (because the right-most digit must be a 0). As illustrated below, there are nine choices for the left-most digit (the digits 1 through 9) and ten choices for the middle digit (the digits 0 through 9). Hence N(A 1) = 9· 10 = 90.

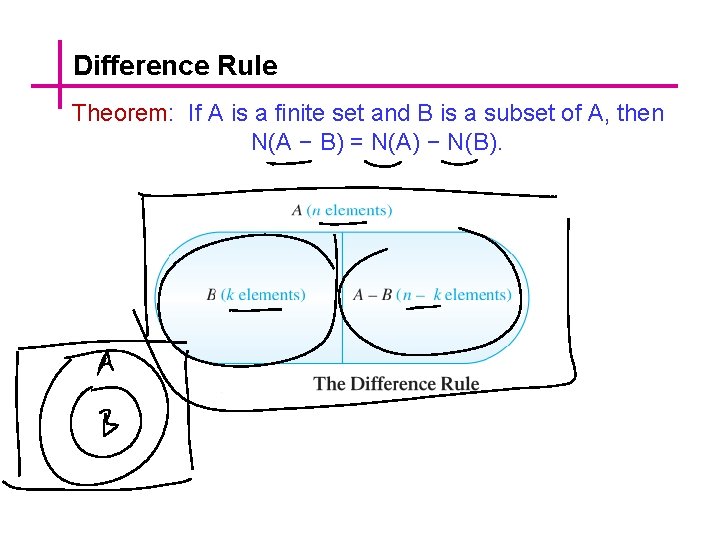
Difference Rule Theorem: If A is a finite set and B is a subset of A, then N(A − B) = N(A) − N(B).

Number of PINs with Repetition we formed PINs using four symbols, either letters of the alphabet or digits, and supposing that letters could be repeated. Now suppose that repetition is allowed. a. How many PINs contain repeated symbols? Solution: There are 364=1, 679, 616 PINs when repetition is allowed, and by there are 1, 413, 720 PINs when repetition is not allowed. Thus, by the difference rule, there are 1, 679, 616 − 1, 413, 720 = 265, 896

The Inclusion/Exclusion Rule Example Counting Elements of a General Union a. How many integers from 1 through 1, 000 are multiples of 3 or multiples of 5? b. How many integers from 1 through 1, 000 are neither multiples of 3 nor multiples of 5?

Cont… Solution: a. Let A = the set of all integers from 1 through 1, 000 that are multiples of 3. Let B = the set of all integers from 1 through 1, 000 that are multiples of 5. A ∪ B = the set of all integers from 1 through 1, 000 that are multiples of 3 or multiples of 5 A ∩ B = the set of all integers from 1 through 1, 000 that are multiples of both 3 and 5

Cont… There are 333 multiples of 3 from 1 through 1, 000, and so N(A) = 333 Similarly, each multiple of 5 from 1 through 1, 000 has the form 5 k, for some integer k from 1 through 200.

Cont… Thus there are 200 multiples of 5 from 1 through 1, 000 and N(B) = 200. Finally, each multiple of 15 from 1 through 1, 000 has the form 15 k, for some integer k from 1 through 66 (since 990 = 66· 15). b. There are 1, 000 integers from 1 through 1, 000, and by part (a), 467 of these are multiples of 3 or multiples of 5. Thus, by the set difference rule, there are 1, 000 − 467 = 533 that are neither multiples of 3 nor multiples of 5.

Pigeon Hole Principle

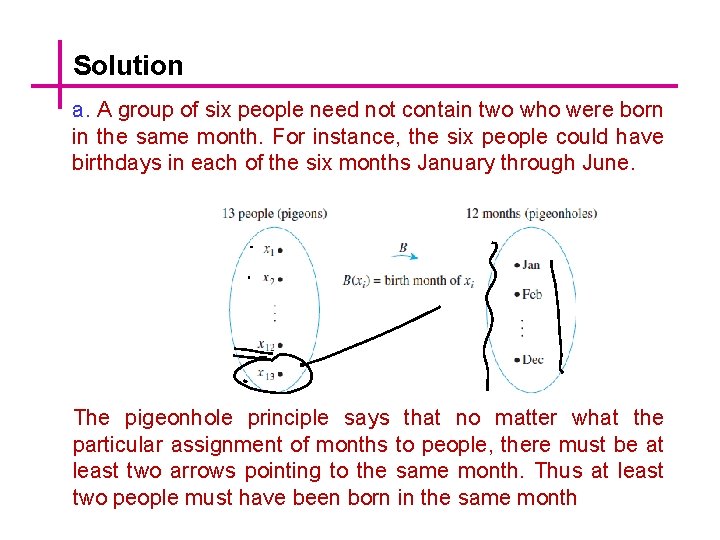
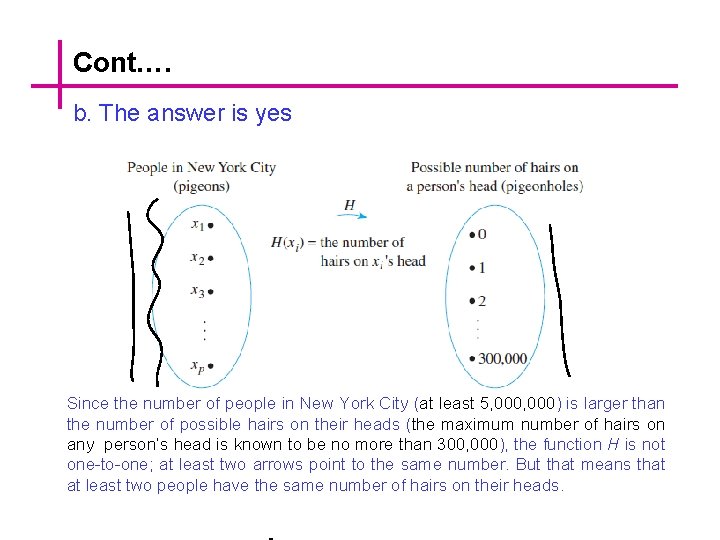
The Pigeonhole Principle A function from one finite set to a smaller finite set cannot be one-to-one: There must be a least two elements in the domain that have the same image in the co-domain. Applying the Pigeonhole Principle a. In a group of six people, must there be at least two who were born in the same month? In a group of thirteen people, must there be at least two who were born in the same month? Why? b. Among the residents of New York City, must there be at least two people with the same number of hairs on their heads? Why?

Solution a. A group of six people need not contain two who were born in the same month. For instance, the six people could have birthdays in each of the six months January through June. The pigeonhole principle says that no matter what the particular assignment of months to people, there must be at least two arrows pointing to the same month. Thus at least two people must have been born in the same month

Cont…. b. The answer is yes Since the number of people in New York City (at least 5, 000) is larger than the number of possible hairs on their heads (the maximum number of hairs on any person’s head is known to be no more than 300, 000), the function H is not one-to-one; at least two arrows point to the same number. But that means that at least two people have the same number of hairs on their heads.

Examples Finding the Number to Pick to Ensure a Result A drawer contains ten black and ten white socks. You reach in and pull some out without looking at them. What is the least number of socks you must pull out to be sure to get a matched pair? Explain how the answer follows from the pigeonhole principle. Solution: If you pick just two socks, they may have different colors. But when you pick a third sock, it must be the same color as one of the socks already chosen. Hence the answer is three

Cont… Selecting a Pair of Integers with a Certain Sum Let A = {1, 2, 3, 4, 5, 6, 7, 8}. a. If five integers are selected from A, must at least one pair of the integers have a sum of 9? b. If four integers are selected from A, must at least one pair of the integers have a sum of 9? Solution: a. Yes. Partition the set A into the following four disjoint subsets: {1, 8}, {2, 7}, {3, 6}, and {4, 5} Observe that each of the integers in A occurs in exactly one of the four subsets and that the sum of the integers in each subset is 9. Thus if five integers from A are chosen, then by the pigeonhole principle, two must be from the same subset. It follows that the sum of these two integers is 9.

Cont… More formally, by the pigeonhole principle, since P is not one-to-one, there are integers ai and aj such that P(ai ) = P(aj ) and ai = aj. But then, by definition of P, ai and aj belong to the same subset. Since the elements in each subset add up to 9, ai + aj = 9.

Cont… b. The answer is no. This is a case where the pigeonhole principle does not apply; the number of pigeons is not larger than the number of pigeonholes. For instance, if you select the numbers 1, 2, 3, and 4, then since the largest sum of any two of these numbers is 7, no two of them add up to 9. Generalized Pigeonhole Principle For any function f from a finite set X with n elements to a finite set Y with m elements and for any positive integer k, if k < n/m, then there is some y ∈ Y such that y is the image of at least k + 1 distinct elements of X.

Applying the Generalized Pigeonhole Principle Show the generalized pigeonhole principle implies that in a group of 85 people, at least 4 must have the same last initial. Solution: In this example the pigeons are the 85 people and the pigeonholes are the 26 possible last initials of their names. Note that 3 < 85/26 ≈ 3. 27. Consider the function L from people to initials defined by the following arrow diagram

Applying the Generalized Pigeonhole Principle Since 3 < 85/26, the generalized pigeonhole principle states that some initial must be the image of at least four (3 + 1) people. Thus at least four people have the same last initial.

Counting the Number of Elements in an Intersection A professor in a discrete mathematics class passes out a form asking students to check all the mathematics and computer science courses they have recently taken. The finding is that out of a total of 50 students in the class, 30 took pre calculus; 16 took both pre calculus and Java; 18 took calculus; 8 took both calculus and Java; 26 took Java; 47 took at least one of the three courses. 9 took both pre calculus and calculus; Find a. How many students did not take any of the three courses? b. How many students took all three courses? c. How many students took pre calculus and calculus but not Java? How many students took pre calculus but neither calculus nor Java.

Cont… Solution: a. By the difference rule, the number of students who did not take any of the three courses equals the number in the class minus the number who took at least one course. Thus the number of students who did not take any of the three courses is 50 − 47 = 3. b. Let P = the set of students who took pre calculus C = the set of students who took calculus J = the set of students who took Java. Then, by the inclusion/exclusion rule, N(P ∪ C ∪ J ) = N(P) + N(C) + N(J ) − N(P ∩ C) − N(P ∩ J ) − N(C ∩ J ) + N(P ∩ C ∩ J )

Cont… Substituting known values, we get 47 = 30 + 18 + 26 − 9 − 16 − 8 + N(P ∩ C ∩ J ) = 6. c. To answer the questions of part (c), look at the diagram in Figure 16 − 6 = 10 students took pre calculus and calculus but not Java 11 students who took pre calculus but neither of the other two courses

Lecture Summary v Counting Elements v Difference Rule v Inclusion/Exclusion Rule v Pigeon Hole Principle v Generalized Pigeon Hole Principle