Discrete Structures CSC 102 Lecture 17 Previous Lectures

Discrete Structures (CSC 102) Lecture 17

Previous Lectures Summary v Properties of relations v Reflexive, Symmetric and Transitive Relations v Properties of “Less than” relations v Properties of Congruence Modulo 3

Relations

Today’s Lecture v Transitive closure of a relations v Combining Relations v The Relation Induced by a Partition v Equivalence Relations v Equivalence Classes of Congruence Modulo 3

The Transitive Closure of a Relation Let A be a set and R a relation on A. The transitive closure of R is the relation Rt on A that satisfies the following three properties: 1. Rt is transitive. 2. R ⊆ Rt. 3. If S is any other transitive relation that contains R, then Rt ⊆ S.

The Transitive Closure of a Relation Example Let A = {0, 1, 2, 3} and consider the relation R defined on A as follows: R = {(0, 1), (1, 2), (2, 3)}. Find the transitive closure of R. Solution: Every ordered pair in R is in Rt, so {(0, 1), (1, 2), (2, 3)} ⊆ Rt. Thus the directed graph of R contains the arrows shown below.

The Transitive Closure of a Relation Since there arrows going from 0 to 1 and from 1 to 2, Rt must have an arrow going from 0 to 2. Hence (0, 2) ∈ Rt. Then (0, 2) ∈ Rt and (2, 3) ∈ Rt, so since Rt is transitive, (0, 3) ∈ Rt. Also, since (1, 2) ∈ Rt and (2, 3) ∈ Rt, then (1, 3) ∈ Rt. Thus Rt contains at least the following ordered pairs: {(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)}. But this relation is transitive; hence it equals Rt. Note that the directed graph of Rt is as shown below.

Combining Relations • Relations are sets, and therefore, we can apply the usual set operations to them. • If we have two relations R 1 and R 2, and both of them are from a set A to a set B, then we can combine them to R 1 R 2, or R 1 – R 2. • In each case, the result will be another relation from A to B.

Combining Relations There is another important way to combine relations. Definition: Let R be a relation from a set A to a set B and S a relation from B to a set C. The composite of R and S is the relation consisting of ordered pairs (a, c), where a A, c C, and for which there exists an element b B such that (a, b) R and (b, c) S. We denote the composite of R and S by S R. In other words, if relation R contains a pair (a, b) and relation S contains a pair (b, c), then S R contains a pair (a, c).

Combining Relations Example: Let D and S be relations on A = {1, 2, 3, 4}. • D = {(a, b) | b = 5 - a} “b equals (5 – a)” • S = {(a, b) | a < b} “a is smaller than b” • D = {(1, 4), (2, 3), (3, 2), (4, 1)} • S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)} • S D = { (2, 4), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)} • D maps an element a to the element (5 – a), and afterwards S maps (5 – a) to all elements larger than (5 – a), resulting in S D = {(a, b) | 5 – a < b} or S D = {(a, b) | a + b > 5}.

The Relation Induced by a Partition A partition of a set A is a finite or infinite collection of nonempty, mutually disjoint subsets whose union is A. A partition of a set A by subsets A 1, A 2, . . . , A 6.

The Relation Induced by a Partition Definition Given a partition of a set A, the relation induced by the partition, R, is defined on A as follows: For all x, y ∈ A, x R y ⇔ there is a subset Ai of the partition such that both x and y are in Ai.

Example Let A = {0, 1, 2, 3, 4} and consider the following partition of A: {0, 3, 4}, {1}, {2}. Find the relation R induced by this partition. Solution Since {0, 3, 4} is a subset of the partition, 0 R 3 because both 0 and 3 are in {0, 3, 4}, 3 R 0 because both 3 and 0 are in {0, 3, 4}, 0 R 4 because both 0 and 4 are in {0, 3, 4}, 4 R 0 because both 4 and 0 are in {0, 3, 4}, 3 R 4 because both 3 and 4 are in {0, 3, 4}, 4 R 3 because both 4 and 3 are in {0, 3, 4}, Also, 0 R 0 because both 0 and 0 are in {0, 3, 4}, 3 R 3 because both 3 and 3 are in {0, 3, 4}, 4 R 4 because both 4 and 4 are in {0, 3, 4}.

Example (Contd. ) Since {1} is a subset of the partition, 1 R 1 because both 1 and 1 are in {1}, and since {2} is a subset of the partition, 2 R 2 because both 2 and 2 are in {2}. Hence R = { (0, 0), (0, 3), (0, 4), (1, 1), (2, 2), (3, 0), (3, 3), (3, 4), (4, 0), (4, 3), (4, 4) }.

Equivalence Relations Definition Let A be a set and R a relation on A. R is an equivalence relation if, and only if, R is reflexive, symmetric, and transitive. Example For all x, y ∈ A, x R y ⇔ there is a subset Ai of the partition such that both x and y are in Ai. R = { (0, 0), (0, 3), (0, 4), (1, 1), (2, 2), (3, 0), (3, 3), (3, 4), (4, 0), (4, 3), (4, 4) }.

Equivalence Relations Equivalence of Digital Logic Circuits Is an Equivalence Relation Let S be the set of all digital logic circuits with a fixed number n of inputs. Define a relation E on S as follows: For all circuits C 1 and C 2 in S, C 1 E C 2 ⇔ C 1 has the same input/output table as C 2. If C 1 E C 2, then circuit C 1 is said to be equivalent to circuit C 2. Prove that E is an equivalence relation on S. Proof: E is reflexive: Suppose C is a digital logic circuit in S. [We must show that C E C. ] Certainly C has the same input/output table as itself. Thus, by definition of E, C E C [as was to be shown].

Equivalence Relations Equivalence of Digital Logic Circuits Is an Equivalence Relation E is symmetric: Suppose C 1 and C 2 are digital logic circuits in S such that C 1 E C 2. [We must show that C 2 E C 1. ] By definition of E, since C 1 E C 2, then C 1 has the same input/output table as C 2. It follows that C 2 has the same input/output table as C 1. Hence, by definition of E, C 2 E C 1. E is transitive: Suppose C 1, C 2, and C 3 are digital logic circuits in S such that C 1 E C 2 and C 2 E C 3. [We must show that C 1 E C 3. ] By definition of E, since C 1 E C 2 and C 2 E C 3, then C 1 has the same input/output table as C 2 and C 2 has the same input/output table as C 3. It follows that C 1 has the same input/output table as C 3. Hence, by definition of E, C 1 E C 3. Since E is reflexive, symmetric, and transitive, E is an equivalence relation on S.

Equivalence Classes of an Equivalence Relation Suppose A is a set and R is an equivalence relation on A. For each element a in A, the equivalence class of a, denoted [a] and called the class of a, is the set of all elements x in A such that x is related to a by R. In symbols: [a] = {x ∈ A |x R a} Or for all x ∈ A, x ∈ [a] ⇔ x R a.

Equivalence Classes of a Relation Let A = {0, 1, 2, 3, 4} and define a relation R on A as follows: R = {(0, 0), (0, 4), (1, 1), (1, 3), (2, 2), (3, 1), (3, 3), (4, 0), (4, 4)}. The directed graph for R is as shown below. As can be seen by inspection, R is an equivalence relation on A. Find the distinct equivalence classes of R.

Equivalence Classes of a Relation R = {(0, 0), (0, 4), (1, 1), (1, 3), (2, 2), (3, 1), (3, 3), (4, 0), (4, 4)}. First find the equivalence class of every element of A. [0] = {x ∈ A |x R 0} = {0, 4} [1] = {x ∈ A |x R 1} = {1, 3} [2] = {x ∈ A |x R 2} = {2} [3] = {x ∈ A |x R 3} = {1, 3} [4] = {x ∈ A |x R 4} = {0, 4} Note that [0] = [4] and [1] = [3]. Thus the distinct equivalence classes of the relation are {0, 4}, {1, 3}, and {2}.

An Equivalence Relation on a Set of Subsets Let X be the set of all nonempty subsets of {1, 2, 3}. Then X = {{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} Define a relation R on X as follows: For all A and B in X, A R B ⇔ the least element of A equals the least element of B. Prove that R is an equivalence relation on X. R is reflexive: Suppose A is a nonempty subset of {1, 2, 3}. [We must show that A R A]. It is true to say that the least element of A equals the least element of A. Thus, by definition of R, A R A.

An Equivalence Relation on a Set of Subsets X = {{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} For all A and B in X, A R B ⇔ the least element of A equals the least element of B. Prove that R is an equivalence relation on X. R is symmetric: Suppose A and B are nonempty subsets of {1, 2, 3} and A R B. [We must show that B R A. ] Since A R B, the least element of A equals the least element of B. But this implies that the least element of B equals the least element of A, and so, by definition of R, B R A. R is transitive: Suppose A, B, and C are nonempty subsets of {1, 2, 3}, A R B, and B R C. [We must show that A R C. ] Since A R B, the least element of A equals the least element of B and since B R C, the least element of B equals the least element of C. Thus the least element of A equals the least element of C, and so, by definition of R, A R C.

An Equivalence Relation on a Set of Subsets The equivalence class of {1} is the set of all the nonempty subsets of {1, 2, 3} whose least element is 1. Thus [{1}] = {{1}, {1, 2}, {1, 3}, {1, 2, 3}}. The equivalence class of {2} is the set of all the nonempty subsets of {1, 2, 3} whose least element is 2. Thus [{2}] = {{2}, {2, 3}}. The equivalence class of {3} is the set of all the nonempty subsets of {1, 2, 3} whose least element is 3. There is only one such set, namely {3} itself. Thus [{3}] = {{3}}. Since all the nonempty subsets of {1, 2, 3} are in one of the equivalence classes, this is a complete listing. Moreover, these classes are all distinct.

An Equivalence Relation on a Set of Subsets Suppose A is a set, R is an equivalence relation on A, and a and b are elements of A. If a R b, then [a] = [b]. Let A be a set, let R be an equivalence relation on A, and suppose a and b are elements of A such that a R b. [We must show that [a] = [b]. ] Proof that [a] ⊆ [b]: Let x ∈ [a]. [We must show that x ∈ [b]]. Since x ∈ [a] then x R a by definition of class. But a R b by hypothesis. Thus, by transitivity of R, x R b. Hence x ∈ [b], by definition of class. [a] ⊆ [b]

An Equivalence Relation on a Set of Subsets Proof that [b] ⊆ [a]: Let x ∈ [b]. [We must show that x ∈ [a]]. Since x ∈ [b], then x R b by definition of class. Now a R b by hypothesis. Thus, since R is symmetric, b R a also. Then, since R is transitive and x R b and b R a, x R a. Hence, x ∈ [a] by definition of class. [This is what was to be shown]. Thus [b] ⊆ [a]. Since [a] ⊆ [b] and [b] ⊆ [a], it follows that [a] = [b] by definition of set equality.

An Equivalence Relation on a Set of Subsets Theorem: If A is a set, R is an equivalence relation on A, and a and b are elements of A, then either [a] ∩ [b] = ∅ or [a] = [b]. The statement of theorem has the form if p then (q or r ). where p is the statement “A is a set, R is an equivalence relation on A, and a and b are elements of A, ” q is the statement “[a] ∩ [b] = ∅, ” and r is the statement “[a] = [b]. ” To prove theorem, we will prove the logically equivalent statement if (p and not q) then r. That is, we will prove the following: If A is a set, R is an equivalence relation on A, a and b are elements of A, and [a] ∩ [b] ≠ ∅, then [a] = [b].

An Equivalence Relation on a Set of Subsets Proof: Suppose A is a set, R is an equivalence relation on A, a and b are elements of A, and [a] ∩ [b] ≠ ∅. [We must show that [a] = [b]. ] Since [a] ∩ [b] ≠ ∅, there exists an element x in A such that x ∈ [a] ∩ [b]. By definition of intersection, x ∈ [a] and x ∈ [b] and so x R a and x R b by definition of class. Since R is symmetric [being an equivalence relation] and x R a, then a R x. But R is also transitive [since it is an equivalence relation], and so, since a R x and x R b, a R b. Now a and b satisfy the hypothesis of previous theorem. Hence, by that theorem, [a] = [b].

Equivalence Classes of Congruence Modulo 3 Let R be the relation of congruence modulo 3 on the set Z of all integers. That is, for all integers m and n, m R n ⇔ 3 | (m − n) ⇔ m ≡ n (mod 3). Describe the distinct equivalence classes of R. For each integer a, [a] = {x ∈ Z |x R a} = {x ∈ Z | 3 | (x − a)} = {x ∈ Z | x − a = 3 k, for some integer k}. Therefore, [a] = {x ∈ Z | x = 3 k + a, for some integer k}. In particular, [0] = {x ∈ Z| x = 3 k + 0, for some integer k} = {x ∈ Z| x = 3 k, for some integer k} = {. . . − 9, − 6, − 3, 0, 3, 6, 9, . . . },

Equivalence Classes of Congruence Modulo 3 [1] = {x ∈ Z| x = 3 k + 1, for some integer k} = {. . . − 8, − 5, − 2, 1, 4, 7, 10, . . . }, [2] = {x ∈ Z| x = 3 k + 2, for some integer k} = {. . . − 7, − 4, − 1, 2, 5, 8, 11, . . . }. Now since 3 R 0, [3] = [0]. More generally, by the same reasoning, [0] = [3] = [− 3] = [6] = [− 6] =. . . , and so on. Similarly, [1] = [4] = [− 2] = [7] = [− 5] =. . . , and so on. And [2] = [5] = − 1 = [8] = [− 4] =. . . , and so on.

Equivalence Classes of Congruence Modulo 3 Notice that every integer is in class [0], [1], or [2]. Hence the distinct equivalence classes are {x ∈ Z| x = 3 k, for some integer k}, {x ∈ Z| x = 3 k + 1, for some integer k}, and {x ∈ Z| x = 3 k + 2, for some integer k}. In words, the three classes of congruence modulo 3 are (1) The set of all integers that are divisible by 3, (2) The set of all integers that leave a remainder of 1 when divided by 3, and (3) The set of all integers that leave a remainder of 2 when divided by 3.

Equivalence Classes of Congruence Modulo 3 [0] = {. . . − 9, − 6, − 3, 0, 3, 6, 9, . . . }, [1] = {. . . − 8, − 5, − 2, 1, 4, 7, 10, . . . }, [2] = {. . . − 7, − 4, − 1, 2, 5, 8, 11, . . . }. Partition of Z : Z = [0] U [1] U [2] And [0] ∩ [1] ∩ [2] = ø

Lecture Summery v Transitive closure of a relations v Combining Relations v The Relation Induced by a Partition v Equivalence Relations v Equivalence Classes of Congruence Modulo 3

Equivalence of Congruence Modulo n Is an Equivalence Relation If n is any integer with n > 1, congruence modulo n is an equivalence relation on the set of all integers. The distinct equivalence classes of the relation are the sets [0], [1], [2], . . . , [n − 1], where for each a = 0, 1, 2, . . . , n − 1, [a] = {m ∈ Z |m ≡ a (mod n)}, or, equivalently, [a] = {m ∈ Z | m = a + kn for some integer k}.

Equivalence of Congruence Modulo n Proof: Suppose n is any integer with n > 1. We must show that congruence modulo n is reflexive, symmetric, and transitive. Proof of reflexivity: Suppose a is any integer. To show that a ≡ a (mod n), we must show that n | (a − a). But a − a = 0, and n | 0 because 0 = n · 0. Therefore a ≡ a (mod n).

Equivalence of Congruence Modulo n Proof: Suppose n is any integer with n > 1. We must show that congruence modulo n is reflexive, symmetric, and transitive. Proof of symmetry: Suppose a and b are any integers such that a ≡ b (mod n). We must show that b ≡ a (mod n). But since a ≡ b (mod n), then n | (a − b). Thus, by definition of divisibility, a − b = nk, for some integer k. Multiply both sides of this equation by − 1 to obtain −(a − b) = −nk, or, equivalently, b − a = n(−k). Thus, by definition of divisibility n | (b − a), and so, by definition of congruence modulo n, b ≡ a (mod n).

Equivalence of Congruence Modulo n Proof: Suppose n is any integer with n > 1. We must show that congruence modulo n is reflexive, symmetric, and transitive. Proof of transitivity: Suppose a, b and c are any integers such that a ≡ b (mod n) and b ≡ c (mod n). We must show that a ≡ c (mod n). Since a ≡ b (mod n), then n | (a − b). And b ≡ c (mod n), then n | (b − c). As we know that if m | k and m | p then m | (k+p). Thus, n | (a – b + b − c) = (a − c) a ≡ c (mod n), Therefore Congruence Modulo n relation is an Equivalence relation

Properties of Congruence Modulo n Theorem: Let a, b, and n be any integers and suppose n > 1. The following statements are all equivalent: 1. n | (a − b) 2. a ≡ b (mod n) 3. a = b + kn for some integer k 4. a and b have the same (nonnegative) remainder when divided by n 5. a mod n = b mod n

Modular Arithmetic Theorem: Let a, b, c, d, and n be integers with n > 1, and suppose a ≡ c (mod n) and b ≡ d (mod n). Then 1. (a + b) ≡ (c + d) (mod n) 2. (a − b) ≡ (c − d) (mod n) 3. ab ≡ cd (mod n) 4. a·m ≡ c·m (mod n), for all integers m.

Modular Arithmetic Theorem: Let a, b, c, d, and n be integers with n > 1, and suppose a ≡ c (mod n) and b ≡ d (mod n). Then 3. ab ≡ cd (mod n) Proof of Part 3: Suppose a, b, c, d, and n are integers with n > 1, and suppose a ≡ c (mod n) and b ≡ d (mod n). There exist integers s and t such that a = c + sn and b = d + tn. Then ab = (c + sn)(d + tn) = cd + ctn + snd + sntn = cd + n(ct + sd + stn) Let k = ct + sd + stn. Then k is an integer and ab = cd + nk. Thus ab ≡ cd (mod n).

Modular Arithmetic Verify the following statements. a. 55 + 26 ≡ (3 + 2) (mod 4), b. 55 − 26 ≡ (3 − 2) (mod 4) c. 55· 26 ≡ (3· 2) (mod 4), d. 552 ≡ 32 (mod 4) a. Compute 55 + 26 = 81 and 3 + 2 = 5. By definition of congruence modulo n, to show that 81 ≡ 5 (mod 4), you need to show that 4 | (81 − 5). But this is true because 81 − 5 = 76, and 4 | 76 since 76 = 4· 19. b. Compute 55 − 26 = 29 and 3 − 2 = 1. By definition of congruence modulo n, to show that 29 ≡ 1 (mod 4), you need to show that 4 | (29 − 1). But this is true because 29 − 1 = 28, and 4 | 28 since 28 = 4· 7. c. Compute 55· 26 = 1430 and 3· 2 = 6. By definition of congruence modulo n, to show that 1430 ≡ 6 (mod 4), you need to show that 4 | (1430 − 6). But this is true because 1430 − 6 = 1424, and 4 | 1424 since 1424 = 4· 356. d. Compute 552 = 3025 and 32 = 9. By definition of congruence modulo n, to show that 3025 ≡ 9 (mod 4), you need to show that 4 | (3025 − 9). But this is true because 3025 − 9 = 3016, and 4 | 3016 since 3016 = 4· 754.

Modular Arithmetic Let a, b, and n be integers with n > 1. Then ab ≡ [(a mod n)(b mod n)] (mod n), or, equivalently, ab mod n = [(a mod n)(b mod n)] mod n. In particular, if m is a positive integer, then am ≡ [(a mod n)m] (mod n). Example Find the residue of 55· 26 modulo 4. (55· 26) mod 4 = {(55 mod 4)(26 mod 4)} mod 4 ≡ (3· 2) mod 4 ; because 55 mod 4 = 3 and 26 mod 4 = 2 ≡ 6 mod 4 ≡ 2

Modular Arithmetic Computing ak mod n When k Is a Power of 2 Find 1444 mod 713. Solution: We can write 1444 = (1442)2. Then 1444 mod 713 = (1442)2 mod 713 = (1442 mod 713)2 mod 713 = (20736 mod 713)2 mod 713 because 1442 = 20736 = 592 mod 713 because 20736 mod 713 = 59 = 3481 mod 713 because 592 = 3481 = 629 because 3481 mod 713 = 629.

Modular Arithmetic Computing ak mod n When k Is Not a Power of 2 Find 1243 mod 713. Solution: First write the exponent as a sum of powers of 2: 43 = 25 + 23 + 2 + 1 = 32 + 8 + 2 + 1. Next compute powers of 12. 12 mod 713 = 12 122 mod 713 = 144 124 mod 713 = 1442 mod 713 = 59 128 mod 713 = 592 mod 713 = 629 1216 mod 713 = 6292 mod 713 = 639 1232 mod 713 = 6392 mod 713 = 485

Modular Arithmetic 1243 = 1232+8+2+1 = 1232 · 128 · 122 · 121 1243 mod 713 = {(1232 mod 713)·(128 mod 713)·(122 mod 713)·(12 mod 713)} mod 713 = (485· 629· 144· 12) mod 713 = 527152320 mod 713 = 48.

Modular Arithmetic Caesar cipher Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described it in 1978

Partial Order Relations Definition Let R be a relation defined on a set A. R is a partial order relation if, and only if, R is reflexive, antisymmetric, and transitive. Example: The “Subset” Relation Let A be any collection of sets and define the “subset” relation, ⊆, on A as follows: For all U, V ∈ A , U ⊆ V ⇔ for all x, if x ∈ U then x ∈ V. Prove that the subset relation is a partial order relation.

Partial Order Relations The “Subset” Relation U ⊆ V ⇔ for all x, if x ∈ U then x ∈ V. For ⊆ to be antisymmetric means that for all sets U and V in A if U ⊆ V and V ⊆ U then U = V. But this is true by definition of equality of sets.

Partial Order Relations The “Less Than or Equal to” Relation Let S be a set of real numbers and define the “less than or equal to” relation, ≤, on S as follows: For all real numbers x and y in S, x ≤ y ⇔ x < y or x = y. Show that ≤ is a partial order relation. ≤ is reflexive: For ≤ to be reflexive means that x ≤ x for all real numbers x in S. But x ≤ x means that x < x or x = x, and x = x is always true. ≤ is antisymmetric: For ≤ to be antisymmetric means that for all real numbers x and y in S, if x ≤ y and y ≤ x then x = y. This follows immediately from the definition of ≤ and the trichotomy property, which says that given any real numbers, x and y, exactly one of the following holds: x < y or x = y or x > y.

Partial Order Relations ≤ is transitive: For ≤ to be transitive means that for all real numbers x, y, and z in S if x ≤ y and y ≤ z then x ≤ z. This follows from the definition of ≤ and the transitivity property of order, which says that given any real numbers x, y, and z, if x < y and y < z then x < z. Because ≤ is reflexive, antisymmetric, and transitive, it is a partial order relation.

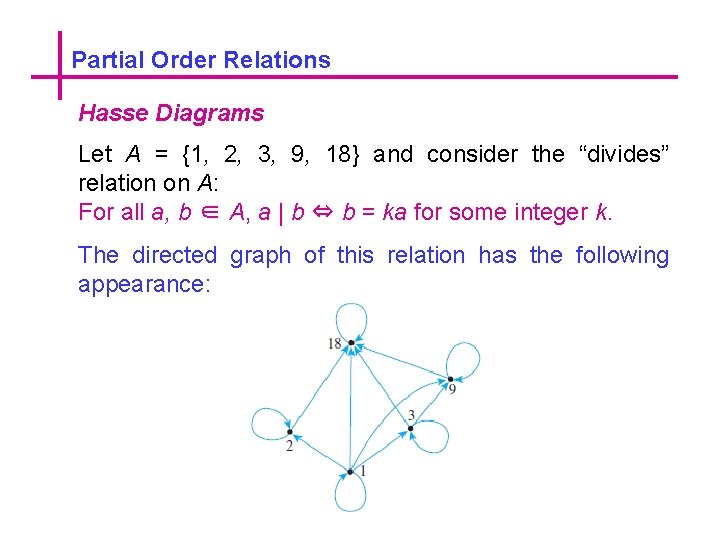
Partial Order Relations Hasse Diagrams Let A = {1, 2, 3, 9, 18} and consider the “divides” relation on A: For all a, b ∈ A, a | b ⇔ b = ka for some integer k. The directed graph of this relation has the following appearance:

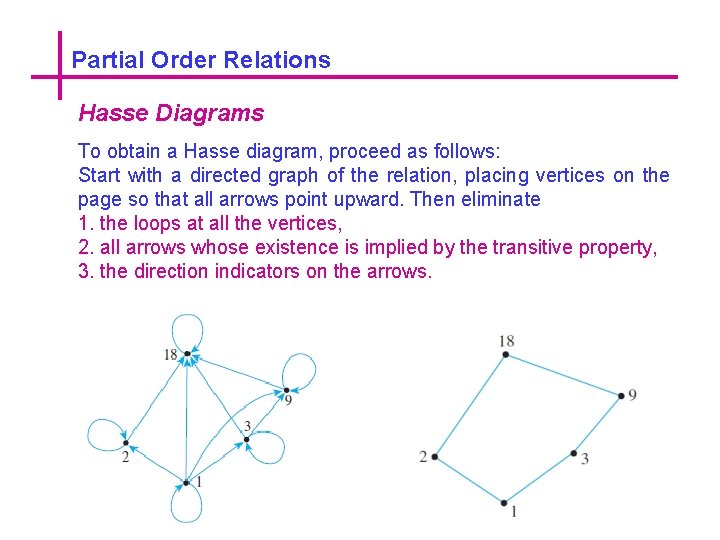
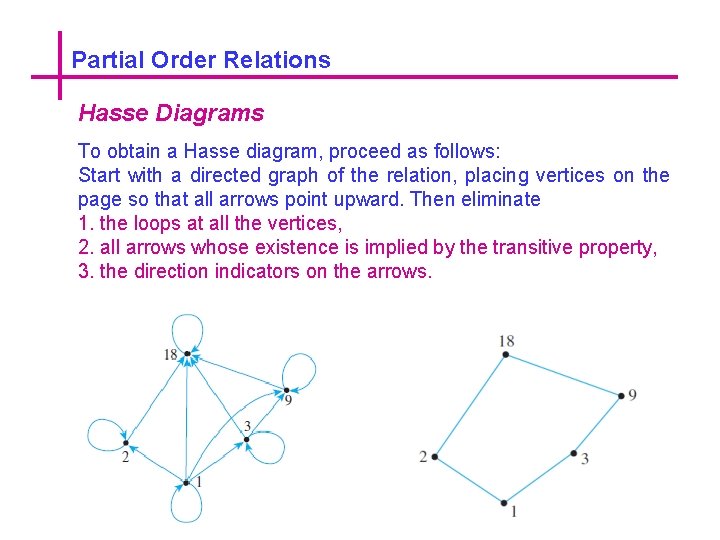
Partial Order Relations Hasse Diagrams To obtain a Hasse diagram, proceed as follows: Start with a directed graph of the relation, placing vertices on the page so that all arrows point upward. Then eliminate 1. the loops at all the vertices, 2. all arrows whose existence is implied by the transitive property, 3. the direction indicators on the arrows.

Partial Order Relations Hasse Diagrams To obtain a Hasse diagram, proceed as follows: Start with a directed graph of the relation, placing vertices on the page so that all arrows point upward. Then eliminate 1. the loops at all the vertices, 2. all arrows whose existence is implied by the transitive property, 3. the direction indicators on the arrows.

Lecture Summery v Properties of relations v Reflexive, Symmetric and Transitive Relations v Properties of “Less than” relations v Properties of Congruence Modulo 3 v Transitive closure of a relations v Combining Relations v The Relation Induced by a Partition