Discrete Structures CSC 102 Lecture 12 Previous Lecture










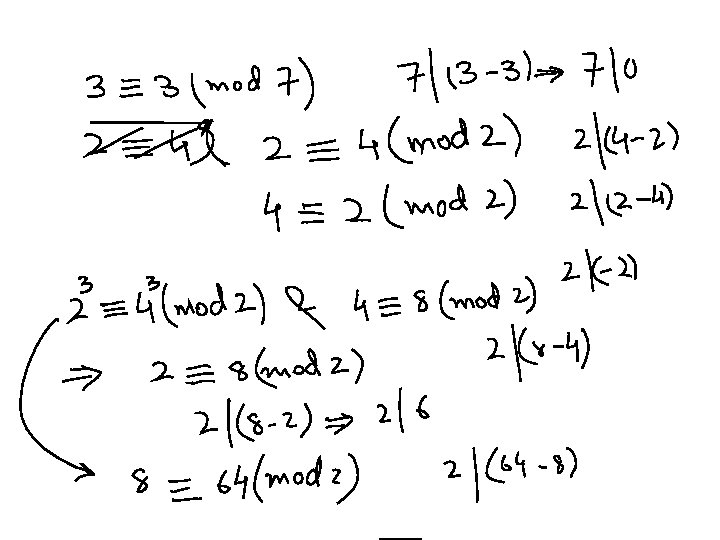











- Slides: 25

Discrete Structures (CSC 102) Lecture 12

Previous Lecture Summary • Floor and Ceiling Functions • Definition of Proof • Methods of Proof • Direct Proof • Disproving by Counterexample. • Indirect Proof: Proof by Contradiction

Methods of Proof and Number Theory

Today's Lecture • Mod Functions • Divisibility and Floor • Mod Congruence • Indirect Proofs • Proof by Contra-positive • Relation between Contradiction and Contra-positive methods of Proof

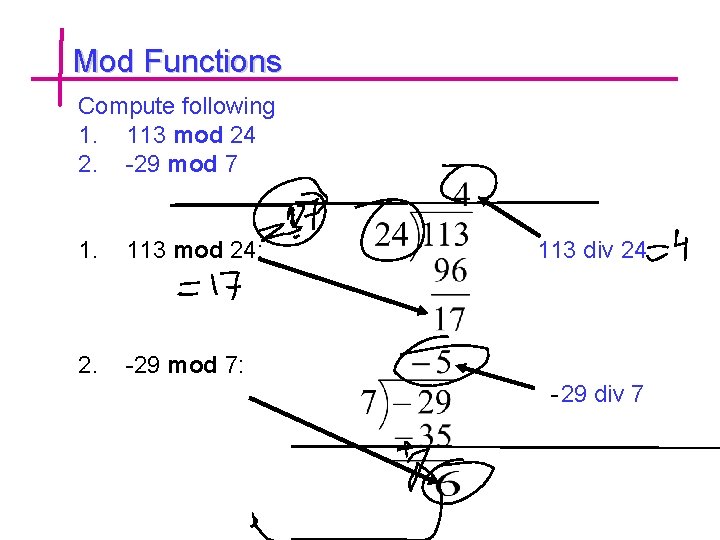
Mod Functions Compute following 1. 113 mod 24 2. -29 mod 7 1. 113 mod 24: 2. -29 mod 7: 113 div 24 -29 div 7

Mod and div Definitions

Divisibility and Floor Theorem

Cont…

Computing div and mod Use the floor notation to compute 3850 div 17 and 3850 mod 17. Sol:

Mod Congruence's Let a, b be integers and n be a positive integer. We say that a is congruent to b modulo n (i. e. a b(mod n) ) iff n | (b-a), implies that there exist some integer k such that b-a = n·k. Note: a mod n = b mod n Which of the following are true? 1. 3 3 (mod 17) 2. 3 -3 (mod 17) 3. 172 177 (mod 5) 4. -13 13 (mod 26)

Cont… 1. 3 3 (mod 17) True: any number is congruent to itself (3 -3 = 0, divisible by all) 2. 3 -3 (mod 17) False: (-3 -3) = 6 isn’t divisible by 17. 3. 172 177 (mod 5) True: 177 -172 = 5 is a multiple of 5 4. -13 13 (mod 26) True: 13 -(-13) = 26 divisible by 26.

Congruence's Identities Let n > 1 be fixed and a, b, c, d be arbitrary integers. Then the following properties holds: a) (Reflexive Property ) a a (mod n). b) (Symmetric Property) If a b(mod n) then b a(mod n). c) ( Transitive Property) If a b(mod n) and b c (mod n) then a c(mod n). d) If a b(mod n) and c d (mod n) then a + c (b + d ) (mod n) and a·c b·d(mod n). e) If a b(mod n) then a + c b+c(mod n) and a·c b·c(mod n). f) If a b(mod n) then a k b k (mod n) for any positive integer k.
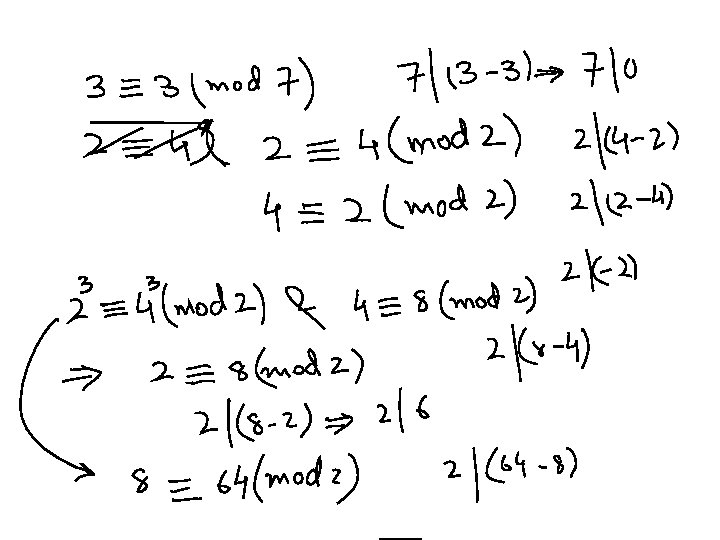


Theorem If k is any integer such that k 1 (mod 3), then k 3 1 (mod 9). Proof: k Z, k 1(mod 3) k 3 1(mod 9) k 1(mod 3) n, k-1 = 3 n n, k = 3 n + 1 n, k 3 = (3 n + 1)3 n, k 3 = 27 n 3 + 27 n 2 + 9 n + 1 n, k 3 -1 = 27 n 3 + 27 n 2 + 9 n n, k 3 -1 = (3 n 3 + 3 n 2 + n)· 9 m, k 3 -1 = m· 9 where m = 3 n 3 + 3 n 2 + n k 3 1(mod 9)

Indirect Proofs Method of Proof by Contra-Positive 1. Express the statement to be proved in the form ∀x in D, if P(x) then Q(x). 2. Rewrite this statement in the contra positive form ∀x in D, if Q(x) is false then P(x) is false. 3. Prove the contra-positive by a direct proof. a. Suppose x is a (particular but arbitrarily chosen) element of D such that Q(x) is false (or ¬Q(x) is true). b. Show that P(x) is false (or ¬P(x) is true).

Proof by Contra-positive Proposition: For all integers n, if n 2 is even then n is even. Contra positive: For all integers n, if n is not even then n 2 is not even. Proof: Suppose n is any odd integer. [We must show that n 2 is odd. ] By definition of odd, n = 2 k + 1 for some integer k. By substitution and algebra, n 2 = (2 k+1)2 = 4 k 2 + 4 k + 1 = 2(2 k 2 + 2 k) + 1. But 2 k 2 + 2 k is an integer because products and sums of integers are integers. So n 2 = 2·(an integer) + 1, and thus, by definition of odd, n 2 is odd.

Relation ship between Contra-positive and Contradiction Proofs In a proof by contraposition, the statement ∀x in D, if P(x) then Q(x) is proved by giving a direct proof of the equivalent statement ∀x in D, if ∼Q(x) then ∼P(x). To do this, you suppose you are given an arbitrary element x of D such that ∼Q(x). You then show that ∼P(x). This is illustrated in Figure

Cont…. To rewrite the proof as a proof by contradiction, you suppose there is an x in D such that P(x) and ¬Q(x). You then follow the steps of the proof by contraposition to deduce the statement ¬P(x). But ¬P(x) is a contradiction to the supposition that P(x) and ¬Q(x). (Because to contradict a conjunction of two statements, it is only necessary to contradict one of them. ) This process is illustrated in Figure

Proof by Contradiction Proposition: For all integers n, if n 2 is even then n is even. Proof: Suppose n is not even integer. Then n is odd integer. By definition of odd, n = 2 k + 1 for some integer k. By substitution and algebra, n 2 = (2 k+1)2 = 4 k 2 + 4 k + 1 = 2(2 k 2 + 2 k) + 1. But 2 k 2 + 2 k is an integer because products and sums of integers are integers. So n 2 = 2·(an integer) + 1, and thus, by definition of odd, n 2 is odd. But n 2 is even in hypothesis. Which is a contradiction because any integer cannot be both even and odd. Thus our supposition was wrong. Hence n is even.

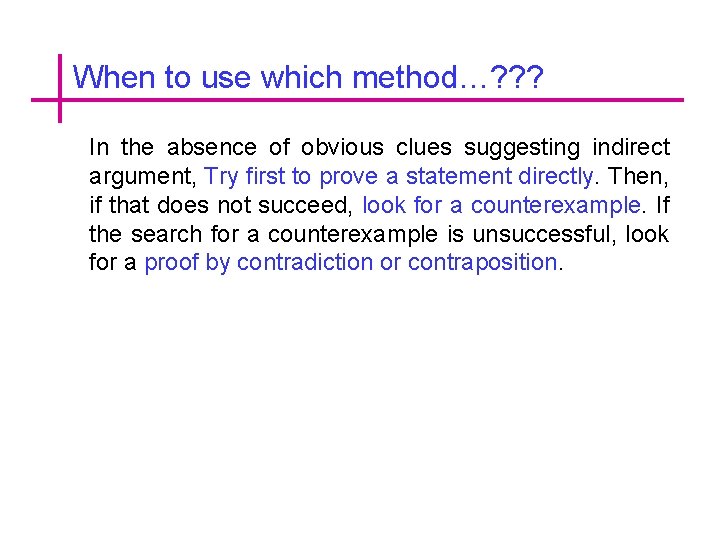
When to use which method…? ? ? In the absence of obvious clues suggesting indirect argument, Try first to prove a statement directly. Then, if that does not succeed, look for a counterexample. If the search for a counterexample is unsuccessful, look for a proof by contradiction or contraposition.

Two Classical Theorems Theorem 1: Proof: is an irrational number.

Cont… m = 2 k for some integer k. m 2 = (2 k)2 = 4 k 2 = 2 n 2. n 2=2 k 2 Consequently, n 2 is even, and so n is even. But we also know that m is even. Hence both m and n have a common factor of 2. But this contradicts the supposition that m and n have no common factors. [Hence the supposition is false and so theorem is true. ]

Theorem 2

Lecture Summary • Mod Functions • Divisibility and Floor • Mod Congruence • Indirect Proofs • Proof by Contra-positive • Relation between Contradiction and Contra-positive methods of Proof