Discrete Structures Counting Ch 6 Dr Muhammad Humayoun










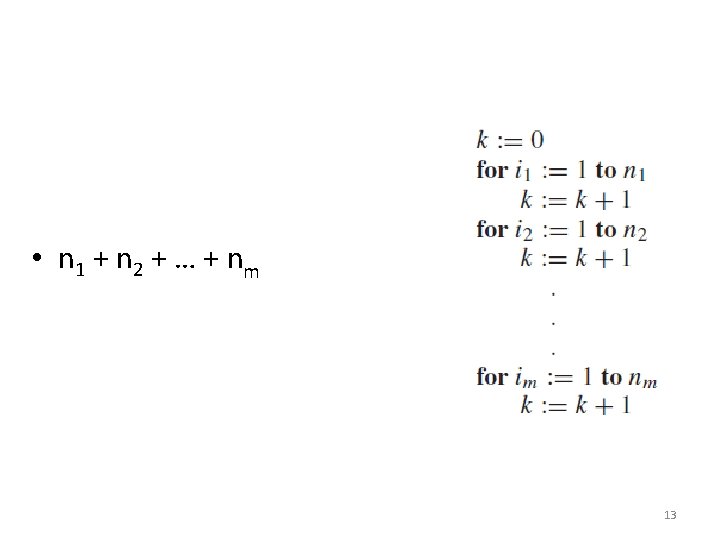
















- Slides: 29

Discrete Structures Counting (Ch. 6) Dr. Muhammad Humayoun Assistant Professor COMSATS Institute of Computer Science, Lahore. mhumayoun@ciitlahore. edu. pk https: //sites. google. com/a/ciitlahore. edu. pk/dstruct/ Modified slides of Dr. M. Atif 1

First Reaction Counting? ? What? ? Are we first graders? ? 2

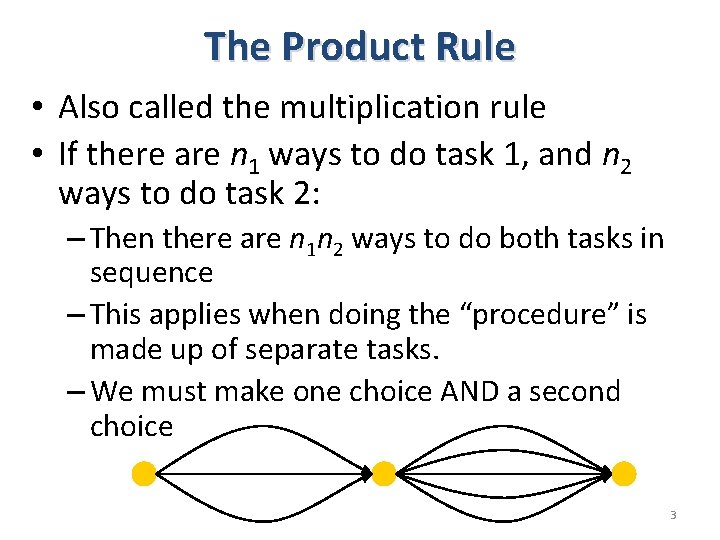
The Product Rule • Also called the multiplication rule • If there are n 1 ways to do task 1, and n 2 ways to do task 2: – Then there are n 1 n 2 ways to do both tasks in sequence – This applies when doing the “procedure” is made up of separate tasks. – We must make one choice AND a second choice 3

Product Rule Example • Sample question – There are 18 math majors and 25 CS majors – How many ways are there to pick one math major and one CS major? • Total is 18 * 25 = 450 possible ways 4

Product Rule Examples Ex. 2: p-386. The chairs of an auditorium are to be labeled with a letter and a positive integer not exceeding 100. What is the largest number of chairs that can be labeled different? Largest Number of chairs = 26 * 100 = 2600 Ex. 3: There are 32 microcomputers in a computer center. Each microcomputer has 24 ports. How many different ports to a microcomputer in the center are there. Two tasks – first picking a microcomputer and then picking a post on this microcomputer. Total no. of ways = 32 * 24 = 768 ports 5

Product Rule Examples Ex. 1: p-386. A new company with just two employees, rents a floor of a building with 12 offices. How many ways are there to assign different offices to these two employees? Possible ways of allotment of any office to first employee = 12 Possible ways of allotment of any of the remaining office to second employee = 11 All possible ways of allotment of offices to two employees = 12 * 11 = 132 See Example 4, 5 6

Product Rule Examples More sample questions… • How many strings of 4 decimal digits… a) Do not contain the same digit twice? We want to chose a digit, then another that is not the same, then another… • • First digit: 10 possibilities Second digit: 9 possibilities (all but first digit) Third digit: 8 possibilities Fourth digit: 7 possibilities Total = 10*9*8*7 = 5040 b) End with an even digit? First three digits have 10 possibilities Last digit has 5 possibilities Total = 10*10*10*5 = 5000 7

More examples • How many different bit strings of length 7 are there? • 27 = 128 different bit strings of length seven. • How many different license plates are available if each plate contains a sequence of three upper case letters followed by three digits. • Choices for 3 upper case letter: 26 * 26 • Choices for 3 digits: 10 * 10 • Total choices: 263 · 103 8

More Examples • What is the value of k after the following code, where n 1, n 2, . . . , nm are +ve integers: n 1* n 2*. . . * nm 9

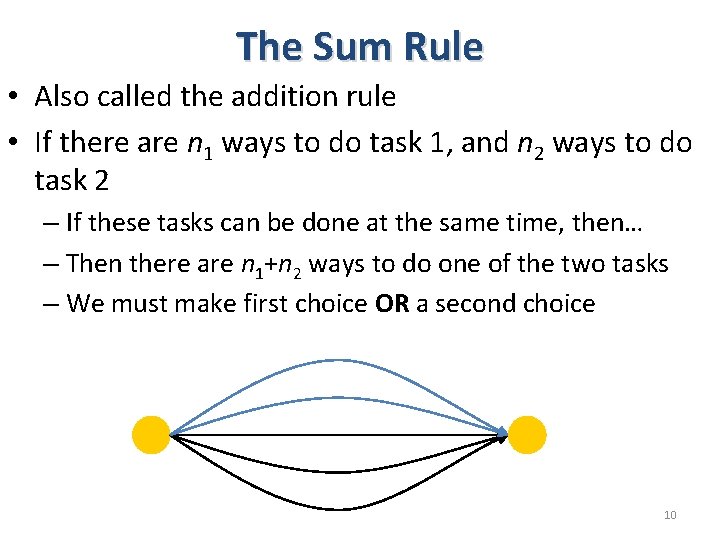
The Sum Rule • Also called the addition rule • If there are n 1 ways to do task 1, and n 2 ways to do task 2 – If these tasks can be done at the same time, then… – Then there are n 1+n 2 ways to do one of the two tasks – We must make first choice OR a second choice 10

Sum Rule Examples More sample questions • How many strings of 4 decimal (non-zero)digits… • Have exactly three digits that are 9 s? – The string can have: • • • – – The non-9 as the first digit OR the non-9 as the second digit OR the non-9 as the third digit OR the non-9 as the fourth digit Thus, we use the sum rule For each of those cases, there are 9 possibilities for the non 9 digit (any number other than 9) Thus, the answer is 9+9+9+9 = 36 11

Sum Rule Examples • Sample question – There are 18 math majors and 25 CS majors – How many ways are there to pick one math major or one CS major? • Total is 18 + 25 = 43 12
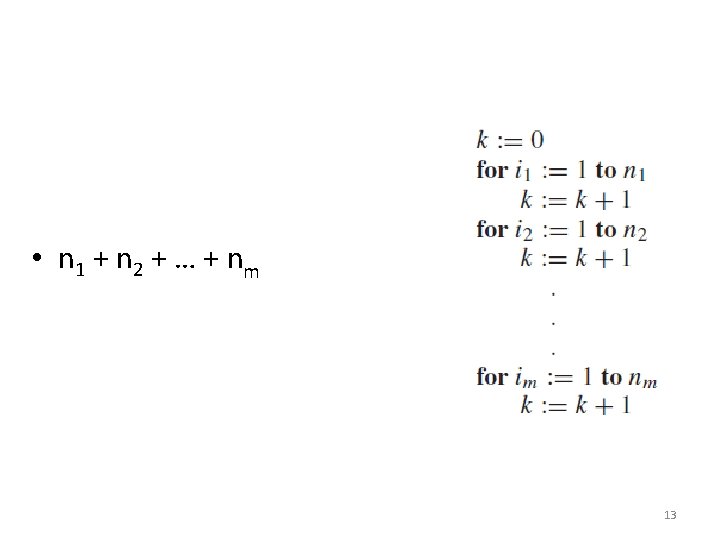

Sum Rule Examples Ex. 11: Suppose that either a member of the mathematics faculty or a student who is mathematics major is chosen as a representative to a university committee. How many different choices are there for this representative if there are 37 members of the math faculty and 83 math students. All possible ways to pick a representative = 37 + 83 = 120 See Ex. 12. Exercise Q. 1, 3 14

Misc Examples There are 18 mathematics majors and 325 computer science majors at a college • In how many ways can two representatives be picked so that one is a mathematics major and the other is a computer science major? 18. 325 • In how many ways can one representative be picked who is either a mathematics major or a computer science major? 18 + 325 15

• A multiple-choice test contains 10 questions. There are four possible answers for each question. – In how many ways can a student answer the questions on the test if the student answers every question? 4 * …. * 4 (10 times)= 410 – In how many ways can a student answer the questions on the test if the student can leave answers blank? 510 16

• A particular brand of shirt comes in 12 colors, has a male version and a female version, and comes in three sizes for each gender. How many different types of this shirt are made? • 12 * ( 3 + 3) 17

How many strings of three decimal digits • do not contain the same digit three times? – 10*10*10 – 10 = 990 • begin with an odd digit? – 5* 10*10 = 500 • have exactly two digits that are 4 s? – 10 + 10 = 30 18

• A committee is formed consisting of one representative from each of the 50 states in the United States, where the representative from a state is either the governor or one of the two senators from that state. How many ways are there to form this committee? • (1+1+1)50 19

• How many license plates can be made using either three digits followed by three uppercase English letters or three uppercase English letters followed by three digits? • 10^3 * 26^3 + 26^3 * 10^3 20

• How many license plates can be made using either two uppercase English letters followed by four digits or two digits followed by four uppercase English letters? • 26^2*10^4 + 10^2*26^4 21

6. 2 The Pigeonhole Principle • Suppose that there are 9 pigeonholes for a flock of 10 pigeons. Because there are 10 pigeons but only 9 pigeonholes, a least one of these 9 pigeonholes must have at least two pigeons in it. • This illustrates the pigeonhole principle. If there are more pigeons than pigeonholes, then there must be at least one pigeonhole with at least two pigeons in it. 22

The Pigeonhole Principle • If k is a positive integer and k + 1 or more objects are placed into k boxes, then there is at least one box containing two or more of the objects. 23

Can be used to demonstrate possibly unexpected results • Among a group of 367 people (randomly chosen), there must be at least two with the same birthday, because there are only 365 possible birthdays. • In any group of 27 English words (randomly chosen), there must be at least two that begin with the same letter, because there are 26 letters in the English alphabet. • Among a set of 15 or more students, at least 3 are born on the same day of the week. 24

More examples Question: How many students must be in a class to guarantee that at least two students receive the same score on the final exam, if the exam is graded on a scale from 0 to 100 points? Ans: There are 101 possible scores on the final. The pigeonhole principle shows that among any 102 students there must be at least 2 students with the same score. 25

The Generalized Pigeonhole Principle • Even more can be said when the number of objects exceeds a multiple of the number of boxes. • Among any set of 21 decimal digits there must be 3 that are the same. • Why? when 21 objects are distributed into 10 boxes, one box must have more than 2 objects. 26

27

28

The Last slide. VIS • How many numbers must be selected from the set {1, 2, 3, 4 , 5, 6} to guarantee that at least one pair of these numbers add up to 7? • Sol: • Total numbers = 6 • Possible ways to add up to 7= (1, 6), (2, 5), (3, 4) • We have to select at least 4 numbers, so that at least one pair from above 3 pairs is selected. 29