Discrete Structures Algorithms More on Methods of Proof

Discrete Structures & Algorithms More on Methods of Proof / Mathematical Induction EECE 320 — UBC

Announcements First assignment due Friday • drop-box Quiz during next lecture 2

Quiz sample 1. ) Show that the following statement: For every positive integer n, 2 n n 2 is false 2. ) Show that if x is irrational, then sqrt(x) is irrational. 3

What have we explored so far? Propositional logic Rules of inference Methods of proof Proofs by induction 4

The essential elements of mathematical induction are: • The proposition of interest • The base case • The inductive step 5

Example Prove that 2 n < n! for all n > 3 6

Example Prove that n 3 -n is divisible by 3 for all integers n Do you need to use ‘strong induction’? 7

Example Consider the following game: • Two players. • Players take turns removing any positive number of matches from one of two piles of matches. • The player who takes the last match(es) wins. Show that if the two piles contain the same number of matches, the second player has a guaranteed winning strategy 8

What’s wrong with the following proof using ‘strong induction’? For all non-negative integer n, 5 n=0 Proof: Base case: 5*0=0 Induction step: Suppose that 5 j = 0 for all non-negative integers j, 0 j k. Aim to show that 5(k+1)=0. We can write k+1=i+j with 0 i, j k. 5(k+1)=5(i+j)=5 i+5 j=0+0=0. 9

Recursive definitions Series: Sn = 1 + 2 + 3 + … + n Can be defined as: S 1 = 1 Sn+1 = Sn + (n+1) 10

Recursive definitions Sets: S 3 = {n| n>0, n divisible by 3} Can recursively be defined as: Base step: 3 S 3 Recursive step: if x S 3 and y S 3 then x+y S 3 11

Recursive definitions Structures: A list Ln …is formed by its cells C 1, C 2 , , , Cn A list recursively be defined as: Base step: an empty list is a list. Recursive step: Ln+1 is a list if it is formed by adding a cell C to a list Ln 12

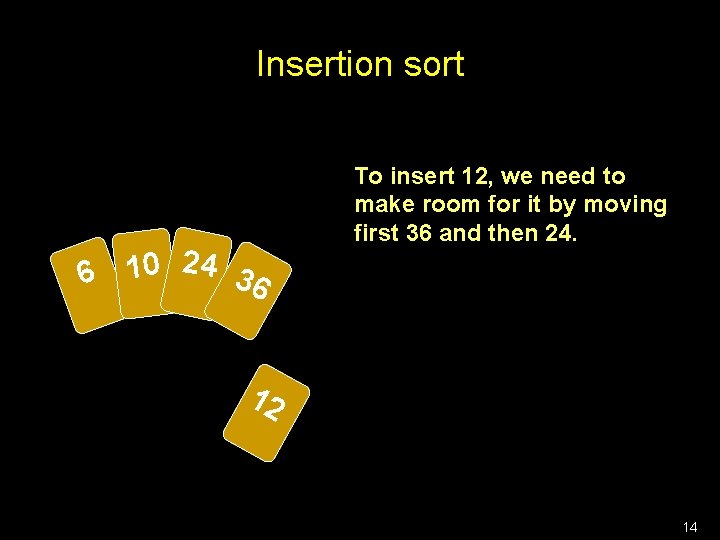
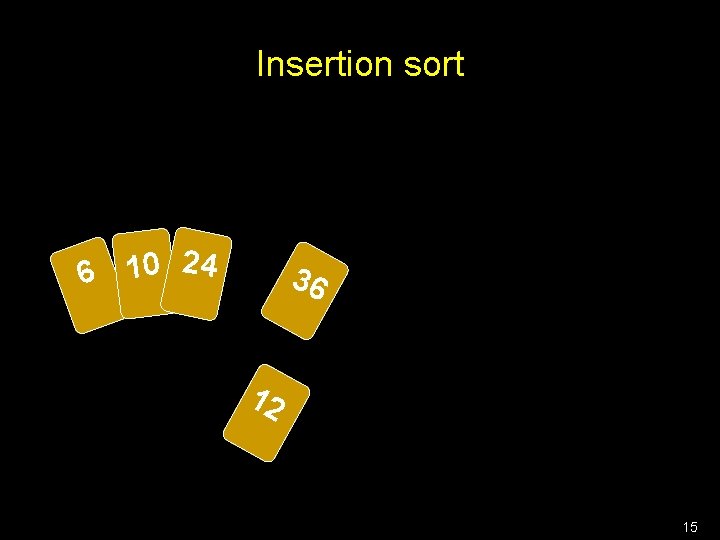
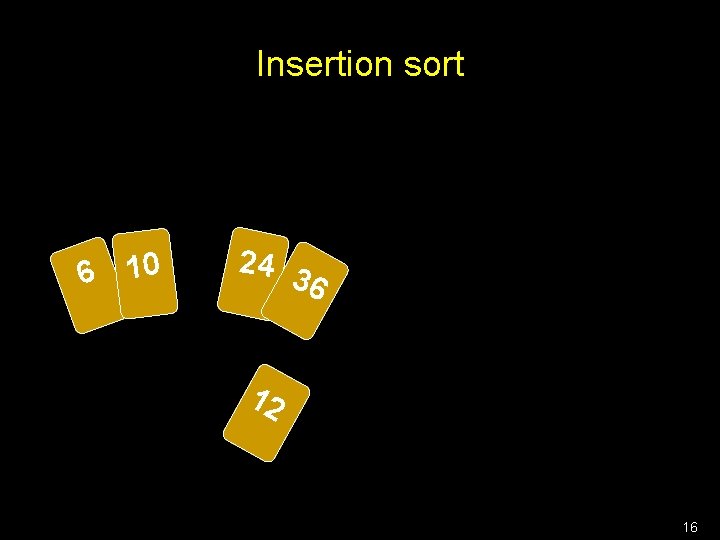
Recursive algorithms Naturally work on all recursive definitions! Example: Insertion sort 13

Insertion sort 6 10 24 36 To insert 12, we need to make room for it by moving first 36 and then 24. 12 14

Insertion sort 6 10 24 36 12 15

Insertion sort 6 10 24 3 6 12 16

Insertion sort Procedure sort (List L): if length(L) 1 return L else C = head (L) T = tail (L) return insert (C, sort(T)) 17

(auxiliary procedure: Insertion) Procedure insert (Cell C, List L): if length(L) = 0 return list(C) else if C < head (L) return list(C, L) else return list(head(L), insert (C, tail(L)) 18

Induction proofs and recursive procedures You can use proofs based on induction to prove: • Correctness invariants • Complexity limits 19

Insertion sort – correctness Procedure sort (List L): if length(L) 1 return L else L 1 sorted C = head (L) if LN sorted T = tail (L) then LN+1 return insert (C, sort(T)) sorted To prove: LN sorted for all lengths N 20

Insertion sort – complexity Procedure sort (List L): if length(L) 1 return L else C = head (L) T = tail (L) return insert (C, sort(T)) P 1 = 0 PN+1 = PN + complexity (insert. N) To find: PN – the average number of operations to sort L 21

In class exercise Give a recursive algorithm to find the maximum of a list of non-negative integers. • Use structural induction to prove correctness • Analyze complexity 22

Better sorting 23

Procedure mergesort (L=a 1, a 2, …. an): if n>1 then m: = n/2 L 1 = a 1, a 2, …. am L 2 = am+1, …. an L = merge (mergesort(L 1), mergesort(L 2)) return L Recursive proof à Correctness àComplexity 24

The essential elements of mathematical induction are: • The proposition of interest • The base case • The inductive step 25

Various uses of induction • Normal • Strong induction Recursive definitions • Induction: To prove correctness properties (invariants) • Induction: To analyze algorithm complexity 26

To understand how to perform computations efficiently, we need to know • How to count! • How to sum a sequence of steps. • Reason about the complexity/efficiency of an algorithm. • Prove the correctness of our analysis. – – – Logic Methods of inference Proof strategies Induction … • (and eventually) How to create better algorithms. 27