Discrete Structures Algorithms Functions Asymptotic Complexity To understand

Discrete Structures & Algorithms Functions & Asymptotic Complexity

To understand how to perform computations efficiently, we need to know – – How to count! How to sum a sequence of steps. Reason about the complexity/efficiency of an algorithm. Prove the correctness of our analysis. • • • Logic Methods of inference Proof strategies Induction … – (and eventually) How to create better algorithms. 2

Functions • We can represent the number of steps needed to achieve a goal as a function of the size of the problem. • Next: A quick refresher on functions – You should know (most of this) from other math/engineering courses. 3

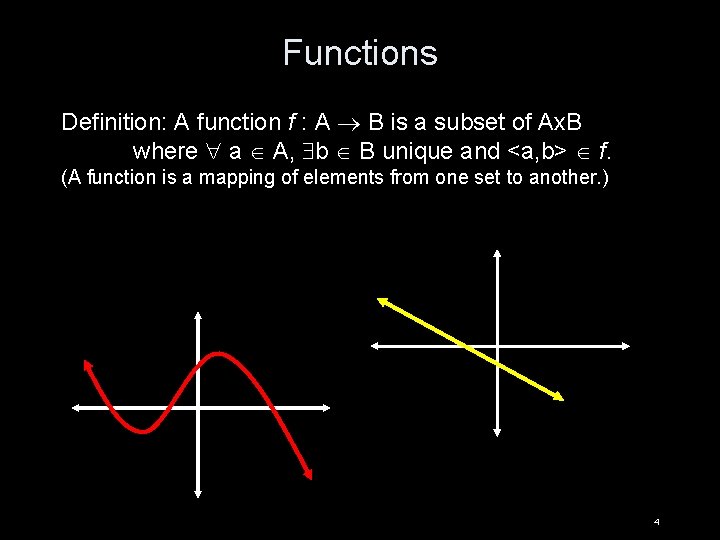
Functions Definition: A function f : A B is a subset of Ax. B where a A, b B unique and <a, b> f. (A function is a mapping of elements from one set to another. ) 4

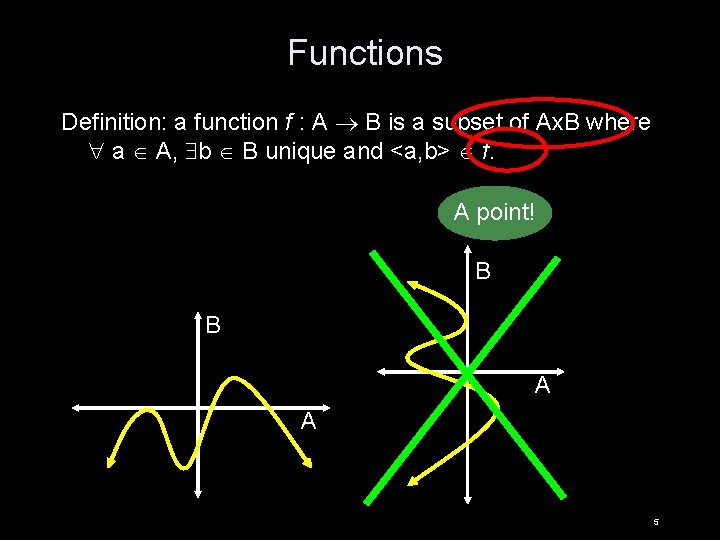
Functions Definition: a function f : A B is a subset of Ax. B where a A, b B unique and <a, b> f. A point! B B A A 5

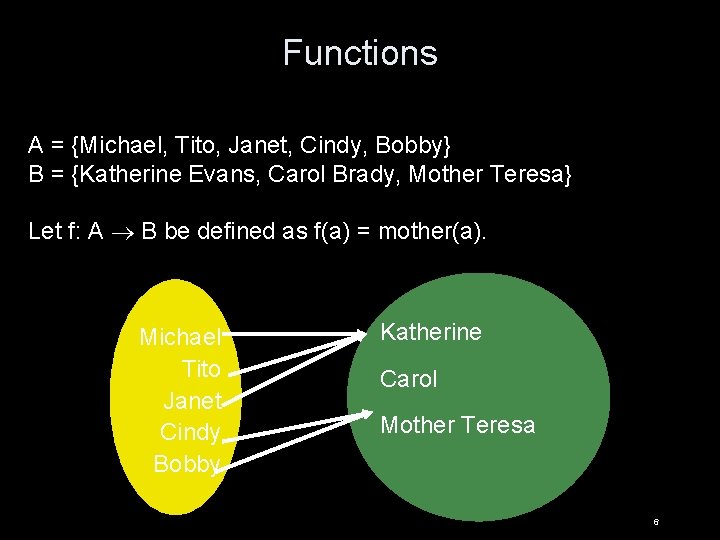
Functions A = {Michael, Tito, Janet, Cindy, Bobby} B = {Katherine Evans, Carol Brady, Mother Teresa} Let f: A B be defined as f(a) = mother(a). Michael Tito Janet Cindy Bobby Katherine Carol Mother Teresa 6

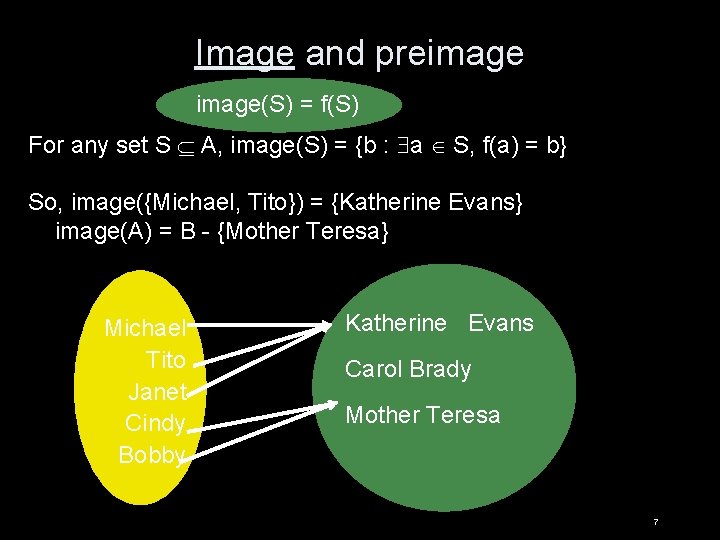
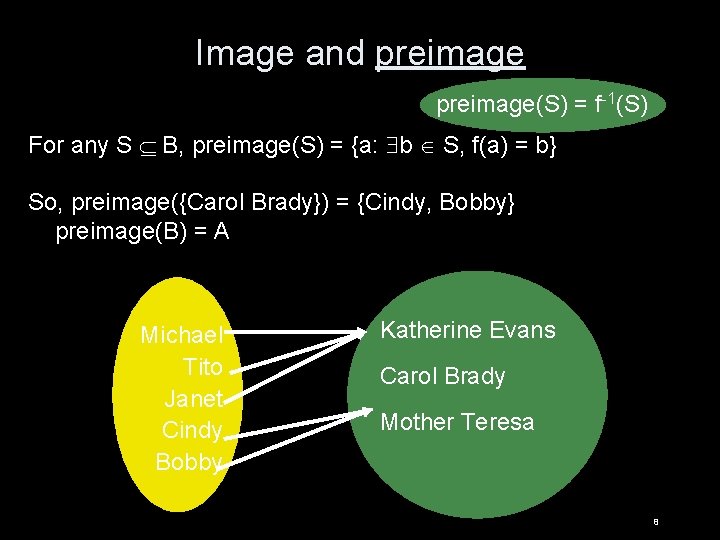
Image and preimage(S) = f(S) For any set S A, image(S) = {b : a S, f(a) = b} So, image({Michael, Tito}) = {Katherine Evans} image(A) = B - {Mother Teresa} Michael Tito Janet Cindy Bobby Katherine Evans Carol Brady Mother Teresa 7

Image and preimage(S) = f-1(S) For any S B, preimage(S) = {a: b S, f(a) = b} So, preimage({Carol Brady}) = {Cindy, Bobby} preimage(B) = A Michael Tito Janet Cindy Bobby Katherine Evans Carol Brady Mother Teresa 8

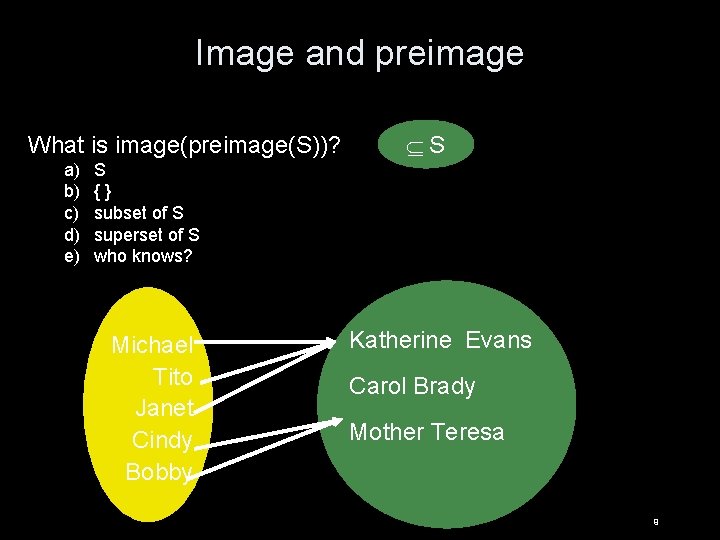
Image and preimage What is image(preimage(S))? a) b) c) d) e) S S {} subset of S superset of S who knows? Michael Tito Janet Cindy Bobby Katherine Evans Carol Brady Mother Teresa 9

Functions and their properties • You should be familiar with these properties (past classes) or • Functions derive many of their properties from sets (they are defined on sets) • As you already know much about sets -> should be able to derive these properties 10

Functions and their properties f(A B) f(A) f(B)? Choose an arbitrary b f(A B), and show that it must also be an element of f(A) f(B). f(A B) = {y : x (A B), f(x) = y} So, x (A B) such that f(x) = y. If x A (it is), then f(x) = y f(A). If x B (it is), then f(x) = y f(B). y f(A), and y f(B), so b f(A) f(B). 11

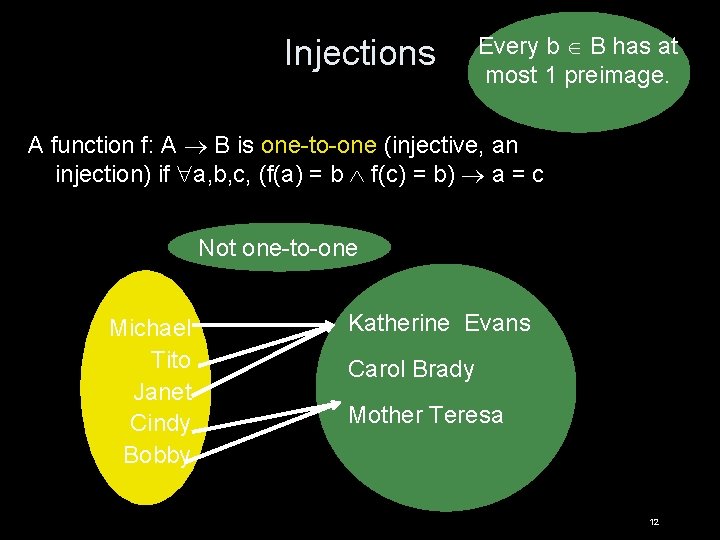
Injections Every b B has at most 1 preimage. A function f: A B is one-to-one (injective, an injection) if a, b, c, (f(a) = b f(c) = b) a = c Not one-to-one Michael Tito Janet Cindy Bobby Katherine Evans Carol Brady Mother Teresa 12

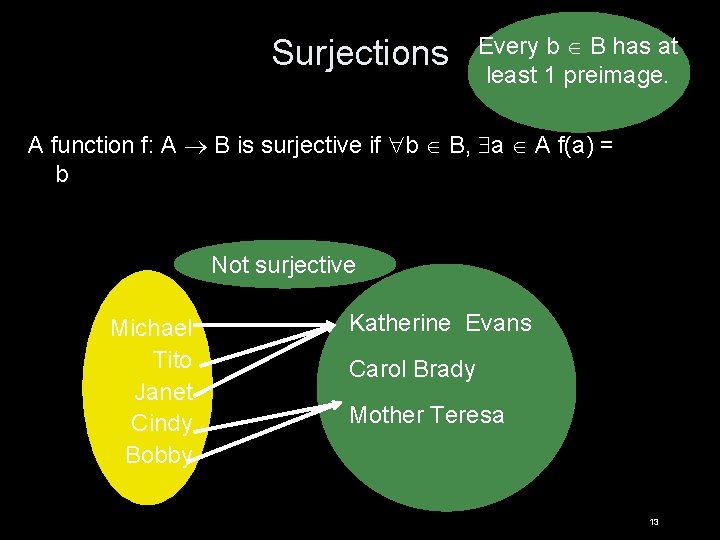
Surjections Every b B has at least 1 preimage. A function f: A B is surjective if b B, a A f(a) = b Not surjective Michael Tito Janet Cindy Bobby Katherine Evans Carol Brady Mother Teresa 13

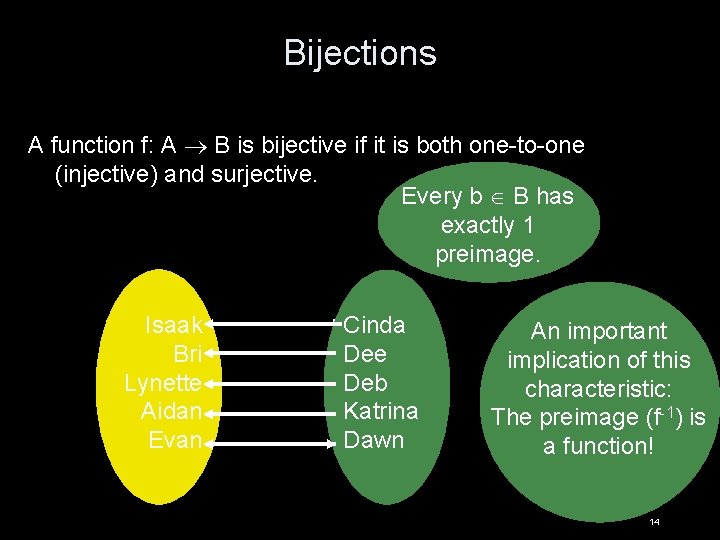
Bijections A function f: A B is bijective if it is both one-to-one (injective) and surjective. Every b B has exactly 1 preimage. Isaak Bri Lynette Aidan Evan Cinda Dee Deb Katrina Dawn An important implication of this characteristic: The preimage (f-1) is a function! 14

Examples Suppose f: R+ R+, f(x) = x 2. Is f one-to-one? yes Is f surjective? yes Is f bijective? yes 15

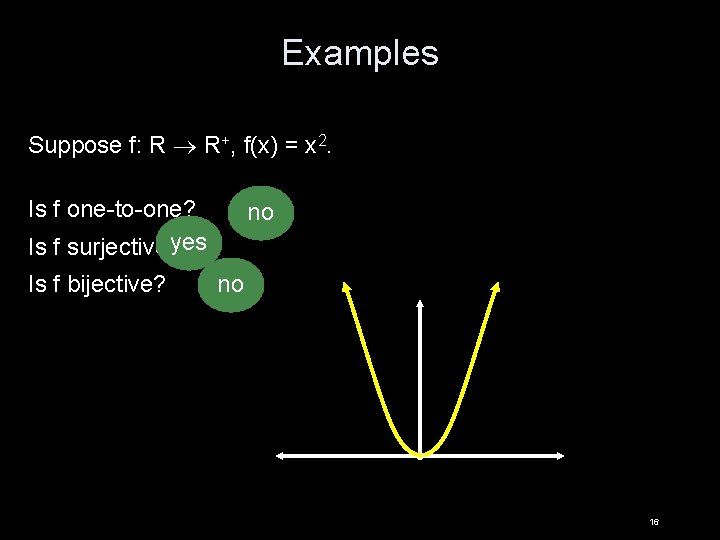
Examples Suppose f: R R+, f(x) = x 2. Is f one-to-one? Is f surjective? yes Is f bijective? no no 16

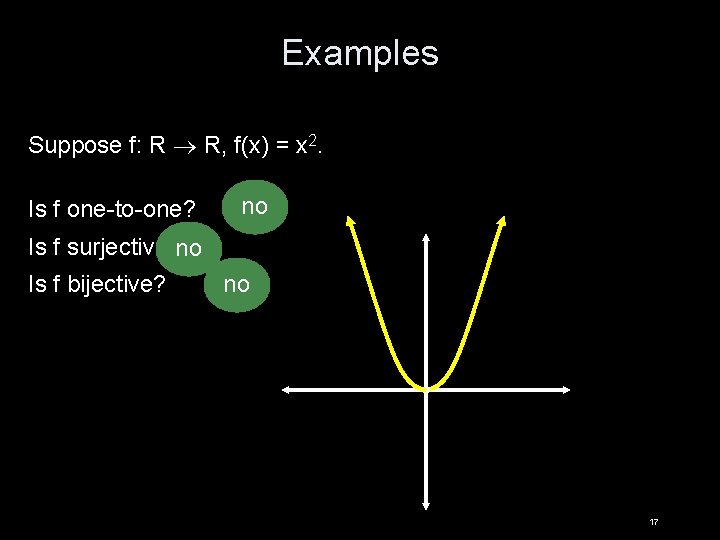
Examples Suppose f: R R, f(x) = x 2. Is f one-to-one? no Is f surjective? no Is f bijective? no 17

Composition of functions Let g: X Y, and f: Y Z be functions. Then the composition of f and g is: (f o g)(x) = f(g(x)) g f 18

Asymptotic complexity

Asymptotic complexity • Goal: Estimate properties (e. g. , running time) of an algorithm as a function of input size n for large n. • Expressed using only the highest-order term in the expression for the exact running time. – Instead of exact running time, say (n 2). • Describes behavior of function in the limit. 20

Asymptotic notation • , O, , o, w • Defined for functions over the natural numbers. – Example: f(n) (n 2). – Describes how f(n) grows in comparison to n 2. • (n 2) define a set of functions; in practice used to compare two function sizes. • The notations describes the rate-of-growth for a set of functions. 21

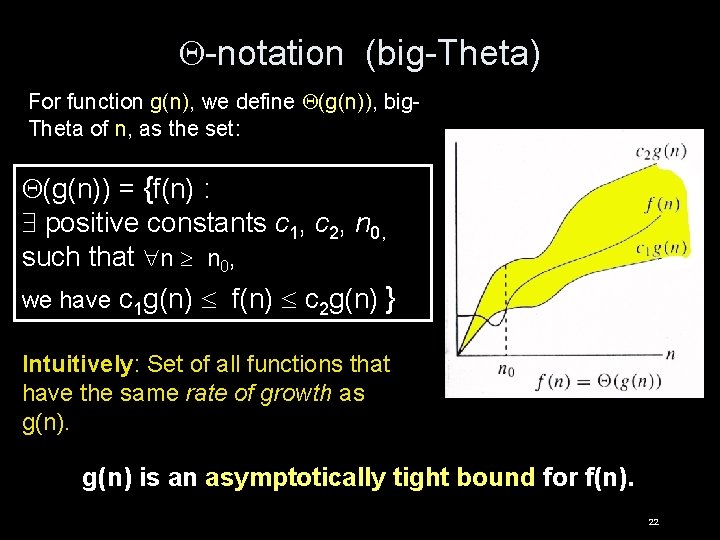
-notation (big-Theta) For function g(n), we define (g(n)), big. Theta of n, as the set: (g(n)) = {f(n) : positive constants c 1, c 2, n 0, such that n n 0, we have c 1 g(n) f(n) c 2 g(n) } Intuitively: Set of all functions that have the same rate of growth as g(n) is an asymptotically tight bound for f(n). 22

-notation For function g(n), we define (g(n)), big. Theta of n, as the set: (g(n)) = {f(n) : positive constants c 1, c 2, n 0, such that n n 0, we have c 1 g(n) f(n) c 2 g(n) } Technically, f(n) (g(n)). Older usage, f(n) = (g(n)). I’ll accept either… g(n) is an asymptotically tight bound for f(n). 23

-notation For function g(n), we define (g(n)), big. Theta of n, as the set: (g(n)) = {f(n) : positive constants c 1, c 2, n 0, such that n n 0, we have c 1 g(n) f(n) c 2 g(n) } If f(n) (g(n)) Then ? (0, ∞, or a constant ) 24

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, c 1 g(n) f(n) c 2 g(n)} For f(n) = 10 n 2 - 3 n (n 2) • What constants for n 0, c 1, and c 2 will work? • Make c 1 a little smaller than the leading coefficient, and c 2 a little bigger. • To compare orders of growth, look at the leading term. Exercise: Prove that n 2/2 -3 n (n 2) 25

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, c 1 g(n) f(n) c 2 g(n)} • Does n 5 (n 4)? • Does 300 n 3 (n 4)? • How about 22 n (2 n)? • Does lg(n!) (n lg n)? – Proof using Stirling’s approximation (in the text) for lg(n!). 26

O-notationf(n) = (g(n)) f(n) = O(g(n)). For function g(n), we define O(g(n)), big. O of n, as the set: (g(n)) O(g(n)) = {f(n): positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } Intuitively: Set of all functions f whose rate of growth is the same as or lower than that of g(n). O(g(n)) is an asymptotic upper bound for f(n). 27

Examples O(g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } • Any linear function an + b is in O(n 2). How? • Show that 3 n 3 O(n 4) for appropriate c and n 0. 28

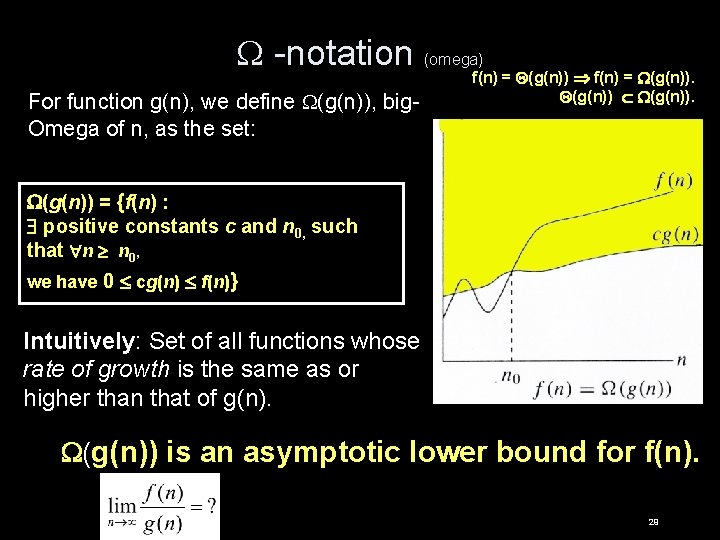
-notation (omega) For function g(n), we define (g(n)), big. Omega of n, as the set: f(n) = (g(n)). (g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 cg(n) f(n)} Intuitively: Set of all functions whose rate of growth is the same as or higher than that of g(n). (g(n)) is an asymptotic lower bound for f(n). 29

Example (g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 cg(n) f(n)} • n (lg n). Choose c and n 0. 30

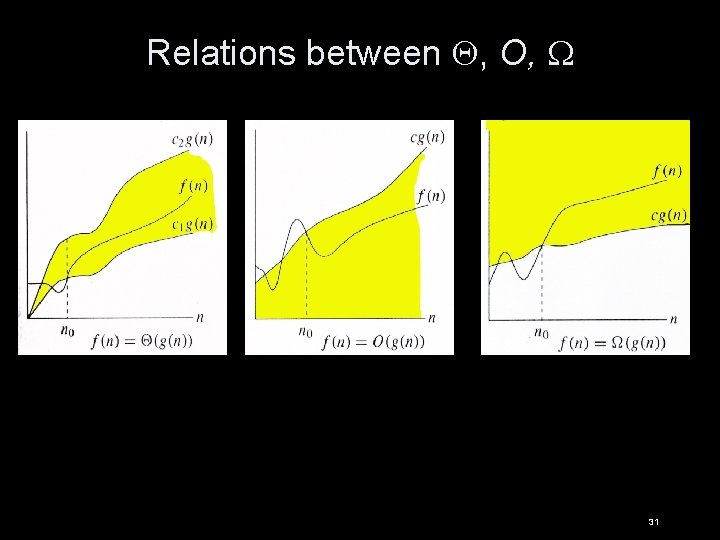
Relations between , O, 31

Relations between , , O Theorem: For any two functions g(n) and f(n), f(n) (g(n)) iff f(n) O(g(n)) and f(n) (g(n)). • (g(n)) = O(g(n)) • In practice, asymptotically tight bounds are obtained from asymptotic upper and lower bounds. 32

Example • Insertion sort takes (n 2) in the worst case, so sorting (as a problem) is O(n 2). Why? • Any sort algorithm must look at each item, so sorting is (n). • In fact, using (e. g. ) merge sort, sorting is Q(n lg n) in the worst case. – No comparison sort to do better in the worst case. [We may not see a proof of this result in this course. ] 33

Asymptotic notation in equations • Can use asymptotic notation in equations to replace expressions containing lower-order terms. • For example, 4 n 3 + 3 n 2 + 2 n + 1 = 4 n 3 + 3 n 2 + (n) = 4 n 3 + (n 2) = (n 3). How do we interpret this? • In equations, (f(n)) always stands for an anonymous function g(n) = (f(n)) – In the example above, (n 2) stands for 3 n 2 + 2 n + 1. 34

o-notation For a given function g(n), the set little-o: o(g(n)) = {f(n): c > 0, n 0 > 0 such that n n 0, we have 0 f(n) < cg(n)}. f(n) becomes insignificant relative to g(n) as n approaches infinity: lim [f(n) / g(n)] = 0. n g(n) is an upper bound for f(n) that is not asymptotically tight. Observe the difference in this definition from previous ones. Why? 35

w –notation (little-omega) For a given function g(n), the set little-omega: (g(n)) = {f(n): c > 0, n 0 > 0 such that n n 0, we have 0 cg(n) < f(n)}. f(n) becomes arbitrarily large relative to g(n) as n approaches infinity: lim [f(n) / g(n)] = . n g(n) is a lower bound for f(n) that is not asymptotically tight. 36

Limits • lim [f(n) / g(n)] = 0 f(n) o(g(n)) n • lim [f(n) / g(n)] < f(n) O(g(n)) n • 0 < lim [f(n) / g(n)] < f(n) (g(n)) n • 0 < lim [f(n) / g(n)] f(n) (g(n)) n • lim [f(n) / g(n)] = f(n) (g(n)) n • lim [f(n) / g(n)] undefined can not say n 37

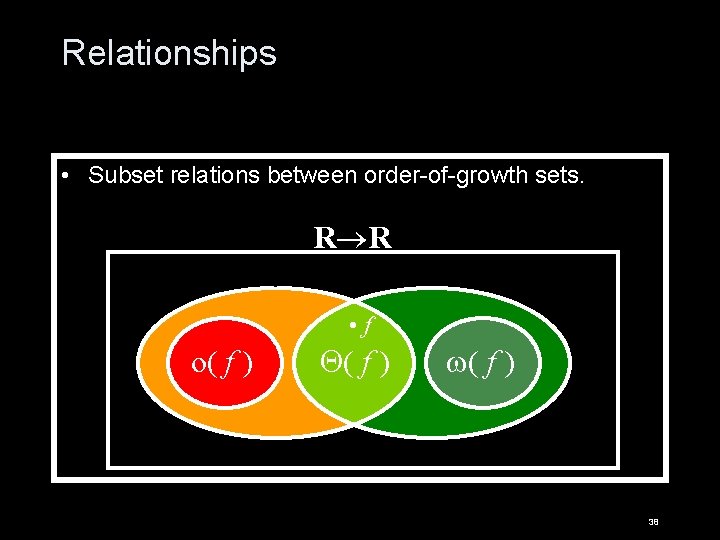
Relationships • Subset relations between order-of-growth sets. O( f ) R R ( f ) • f o( f ) 38

Properties • Transitivity – – – f(n) = (g(n)) & g(n) = (h(n)) f(n) = (h(n)) f(n) = O(g(n)) & g(n) = O(h(n)) f(n) = O(h(n)) f(n) = (g(n)) & g(n) = (h(n)) f(n) = (h(n)) f(n) = o (g(n)) & g(n) = o (h(n)) f(n) = o (h(n)) f(n) = (g(n)) & g(n) = (h(n)) f(n) = (h(n)) • Reflexivity – f(n) = (f(n)) – f(n) = O(f(n)) – f(n) = (f(n)) 39

Properties • Symmetry f(n) = (g(n)) iff g(n) = (f(n)) • Complementarity f(n) = O(g(n)) iff g(n) = (f(n)) f(n) = o(g(n)) iff g(n) = ((f(n)) 40

Common functions

Exponentials • Useful (and elementary) Identities: • Exponentials and polynomials 43

Logarithms x = logba is the exponent for a = bx. Natural log: ln a = logea Binary log: lg a = log 2 a lg 2 a = (lg a)2 lg lg a = lg (lg a) 44

Logarithms and exponentials – Bases • If the base of a logarithm is changed from one constant to another, the value is altered by a constant factor. – Example: log 2 n = log 10 n * log 210 – Base of logarithm is not an issue in asymptotic notation. • Exponentials with different bases differ by a exponential factor (not a constant factor). – Example: 2 n = (2/3)n *3 n. 45

Exercise Express functions in A in asymptotic notation using functions in B. A 5 n 2 + 100 n B 3 n 2 + 2 A (B) A (n 2), n 2 (B) A (B) log 3(n 2) log 2(n 3) A (B) logba = logca / logcb; A = 2 lgn / lg 3, B = 3 lgn, A/B =2/(3 lg 3) nlg 4 3 lg n A (B) alog b = blog a; B =3 lg n=nlg 3; A/B =nlg(4/3) as n lg 2 n n 1/2 A o (B) lim ( lga n / nb ) = 0 (here a = 2 and b = 1/2) A o (B) n 46

Wrap-up • What are the different asymptotic bounds on functions? • How are the asymptotic bounds related? • Asymptotic bounds and algorithmic efficiency 47

Procedure mergesort (L=a 1, a 2, …. an) if n>1 then m: = n/2 L 1 = a 1, a 2, …. am L 2 = am+1, …. an L = merge (mergesort(L 1), mergesort (L 2)) Recursive proof à Correctness à Complexity 48