Discrete structures 2110200 2007 The foundations Counting theory

Discrete structures 2110200 2007 The foundations Counting theory Number theory Graphs & trees

Evaluation n The foundations Counting theory Number theory Graphs & trees 15 % n Final 40 % n n n

Motivation 3 2 --6 4 7 --2 6 8 --5 7 5 --3 8 1 --0 5 4 --0 3 8 --1 2 4 + --6 Ho ? n o i t a t u p m o ec h t o d e w n a c t w fas

Motivation ? A B I J C G E H F D

Motivation K=0 FOR I 1 = 0 TO M { FOR I 2 = 0 TO I 1 { FOR I 3 = 0 TO I 2 { … FOR In = 0 TO In-1 { K=K+1 } … K f o e e valu } } } h t d n i F

T he Foundation s Relational structures

The Foundations Logic and reasoning Set, relation and function Methods of proof

Logic & Reasoning

Historical Aristotle (384 -322 B. C. ) Euclid of Alexandria (325 -265 B. C. ) Chrysippus of Soli (279 -206 B. C. ) George Boole (1815 -1864 A. D. ) Augustus De Morgan (1806 -1871 A. D. ) SYLLOGISTIC REASONING DEDUCTIVE REASONING MODAL LOGIC PROPOSITIONAL LOGIC DE MORGAN’s LAWs

Propositional logic Definition A proposition is a declarative statement that is either true or false but not both.

Theorem : Logical Equivalences, Summary given any propositions p, q and r, a tautology T and a contradiction C, the following logical equivalences hold: • Commutative laws: • Associative laws: • Distributive laws: • Identity laws: • Domination laws: (Universal bound laws) • Idempotent laws: • Negation laws: • Double negative laws: • De Morgan’s laws: • Absorption laws: p q q p (p q) r p (q r) (p q) (p r) p T p p C p p T T p C C p p p T p p C ( p) p (p q) p q p (p q) p

Example Is the following assertion a proposition? This statement is false. No, since this statement is neither “true” nor “false”.

Example The nth statement in a list of 100 statements is Exactly n statements are false. What conclusion can you draw from these statements? At most one statement can be true, then 99 statements are false. That is only the 99 th statement is true.

Example The nth statement in a list of 100 statements is EAxtalcetalsytnnssttaatteem meennttssaarreeffaallssee. . What conclusion can you draw from these statements? 50 first statements are true. The others are false.

Example 99 statements is The nth statement in a list of 100 EAxtalcetalsytnnssttaatteem meennttssaarreeffaallssee. . What conclusion can you draw from these statements? CONTRADICTION

Conditional statement p q Converse The converse of p q is q p. Inverse The inverse of p q is p q. Only if p only if q means If q then p.

Valid arguments Definition An argument is a sequence of statements. All statements excluded the final one are called “hypotheses”, the final statement is called “conclusion”. A argument is the form: p ; q ; r ; … f (read therefore) An argument is valid means that if all hypotheses are true, the conclusion is also true.

Valid arguments Example VALID Given an argument p (q r) ; r ; p q p q r p (q r) r p q T T T T T F T T F F F T T T T F T F T T F F TRUE F ( TFp 1 TF p 2 p. TF 3 … TF pn) q F

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P P Q

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q P

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q P Q

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q Q P

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q Q R P R

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q P Q

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q P R Q R

Rules of inference n n n n n Disjunctive addition Conjunctive simplification Conjunction addition Modus ponens Modus tollens Hypothetical syllogism Disjunctive syllogism Resolution Dilemma P Q P R Q R R

Example Given two logical operators, p | qmeans (p q) p q means (p q) l p m i s a Find p ( r o f n o ti i s o p o r p e . ) q p ( q) (p q)

Example Given two logical operators, p | qmeans (p q) p q means (p q). ) q p ( q) p ( r o f n o tuiival i s o i o p n e o q r p ent to p q usi e l p m i s a ng only . Find a proposit (( p p ) q )

Problem Consider the following statements: All students go to school. John is a student. Diana is a student. …… Of course we can conclude that John goes to school. Diana goes to school. ……

Predicate logic The statement “All students go to school” has two parts: Variable students (denoted by variable x) “go to school” (the predicate) This statement can be denoted by P(x), where P denotes the predicate “go to school”. P(x) is said to be the value of the propositional function P at x. Once a value has been assigned to the variable x, the statement P(x) becomes a proposition and has a truth value.

Quantifiers n n n Universal quantification Existential quantification Unique existential quantification ! Consider a statement x P(x) Q(x). Contraposition Its contrapositive is x Q(x) P(x). Inverse Its inverse is x P(x) Q(x). . Converse Its converse is x Q(x) P(x).

Universal Modus Ponens Consider a statement x P(x) Q(x). For a particular e, P(e) is true, therefore Q(e) is true.

Universal Modus Tollens Consider a statement x P(x) Q(x). For a particular e, Q(e) is true, therefore P(e) is true.

Rules of inferences Universal instantiation x. P(x) P(c) if c U. Universal generalization P(c) for an arbitrary c U x. P(x) Existential instantiation x. P(x) P(c) for some element c U Existential generalization P(c) for some element c U x. P(x)

The order of quantifiers n x y P(x, y) n y x P(x, y) Given a predicate P(x, y): x + y = 0

Nested quantifiers n x P(x) y Q(y) n x y ( P(x) Q(y) ) n y x ( P(x) Q(y) ) n x P(x) x Q(x) n x y ( P(x) Q(y) ) Prenex normal form (PNF)

Example Express the following theorem using the first order predicate logic. Mathematical induction

Set George Cantor (1845 -1918)

Set Definition A set is an unordered collection of objects. The objects are called the elements or members of the set. The number of distinct elements in a set is the cardinality of the set. The Cartesian product of A and B, denoted by A B, is described by { (a, b) | a A b B }.

Defining sets n n L 1={ n| for n = 1 2 3 … } L 2={ n | for n = 1 3 5 7 … } L 3={ n | for n = 1 4 9 16 … } L 4={ n | for n = 3 4 8 22 … }. p i h s r e b m e M m e l b o r p

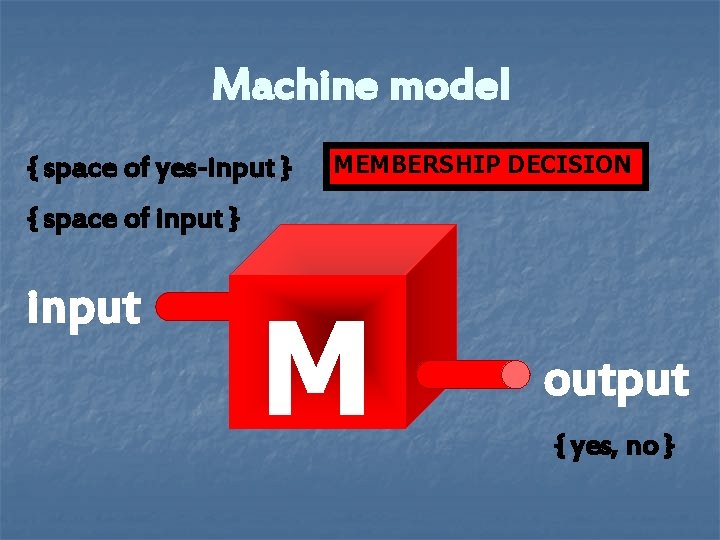
Machine model { space of yes-input } MEMBERSHIP DECISION { space of input } input M output { yes, no }

Example Let U be the universe described by U = { x | 1000 x 9999}. Let Ai be the set of all numbers in U such that the ith position is i. Find the cardin ality of the union of A 1 A 2 A 3 and A 4 ?

Example Let S be the set of all x that x does not contain x. S={x|x x} Note that x is also a set. Does S contain S Russell’s paradox Bertrand Russell (1872 -1970) ?

Set Operators Union Intersection Different Disjoint Complement Power set Mutually disjoint Partition

Set Theorem Given sets A, B and C. • Commutative laws: A B = B A • Associative laws: (A B) C = A (B C) • Distributive laws: A (B C) = (A B) (A C) • Idempotent laws: A U = A • De Morgan’s laws: (A B)c = Ac Bc A B = B A A U = U • Alternative representation for set difference. A-B = A Bc • Absorption laws: A (A B) = A (A B) A = A

Example The symmetric difference of A and B, ( A B ), is the set containing those elements in either A or B, but not in both A and B. (A (B C) )= ( ( A B ) C) ? YES

Example The symmetric difference of A and B, ( A B ), is the set containing those elements in either A or B, but not in both A and B. (A (B C) )= ( ( A B ) Given A C = B C Must it be the case that A = B ? C) ? YES

Multisets Definition Multisets are unordered collections of elements where an element can occur as a member more than once. { m 1. a 1, m 2. a 2, m 3. a 3, …, mr. ar } mi are called the multiplicities of the elements ai. OPERATORS: UNION, INTERSECTION, DIFFERENCE, SUM

Fu. Multisets zzy sets Definition Multisets are unordered collections of elements where an element can occur as a member more 1 m i 0 than once. { m 1. a 1, m 2. a 2, m 3. a 3, …, mr. ar } mi are called the multiplicities of the elements ai. Degree of membership OPERATORS: UNION, INTERSECTION, DIFFERENCE, SUM

Relations & functions

Binary relation Definition Let A, B be sets. A binary relation R from A to B is a subset of the Cartesian product A B. Given (x, y), ordered pair, in A B, x is related to y by R, written x. Ry, iff (x, y) R. Example (the congruence modulo 2 relation) The relation R from Z to Z is defined as follows; for all (x, y) Z Z, x. Ry iff x-y is even. Example, 6 R 2, 120 R 36 etc.

Function Definition A function F from A to B is a relation from A to B, F : A B, that satisfies the following properties: For every x A, there exists y B such that (x, y) F. For all x A, and y, z B, if (x, y) F and (x, z) F then y=z. For (x, y) F , we usually write y =F (x) = image of x under F, and x is called pre-image of y under F. A is called domain of F. B is called co-domain of F. The set of all images of F is called range of F.

Compositions of functions Definition A function f, g from A to B is a function from A to B. (f + g)(x) = f(x) + g(x). (f g)(x) = f(x) g(x) The composition of the functions f and g, denoted by f g, is defined as (f g)(x) = f (g ( x ) )

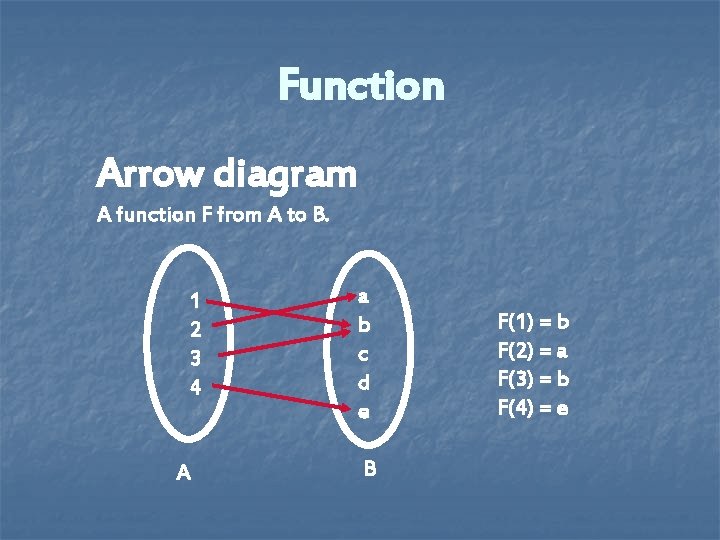
Function Arrow diagram A function F from A to B. 1 2 3 4 A a b c d e B F(1) = b F(2) = a F(3) = b F(4) = e

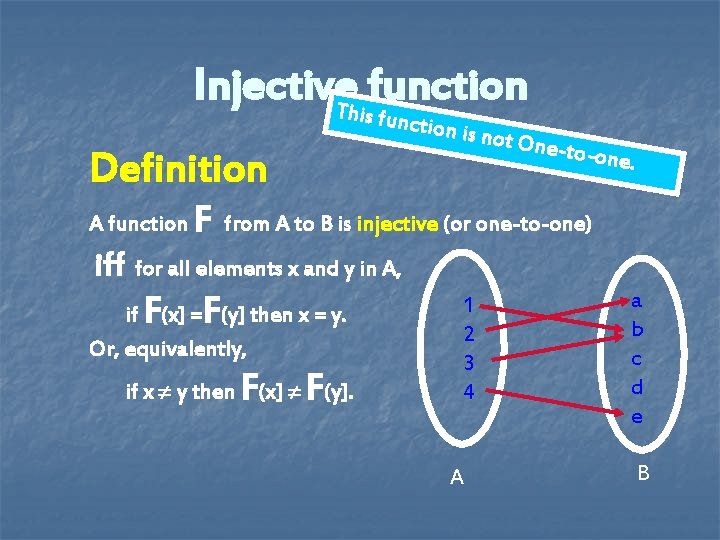
Injective. Thisfunction Definition A function F is not O ne-to-o ne. from A to B is injective (or one-to-one) iff for all elements x and y in A, F F if (x] = (y] then x = y. Or, equivalently, F F if x y then (x] (y]. 1 2 3 4 A a b c d e B

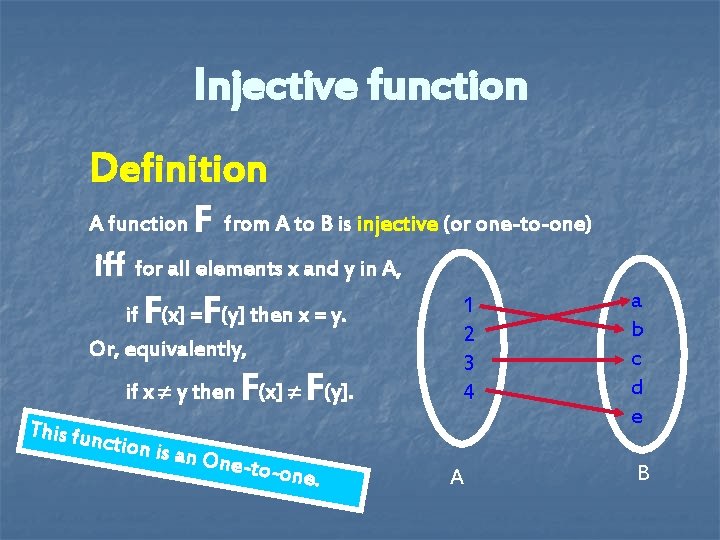
Injective function Definition A function F from A to B is injective (or one-to-one) iff for all elements x and y in A, F F if (x] = (y] then x = y. Or, equivalently, F F if x y then (x] (y]. This fun ction is a n One-t o-one. 1 2 3 4 A a b c d e B

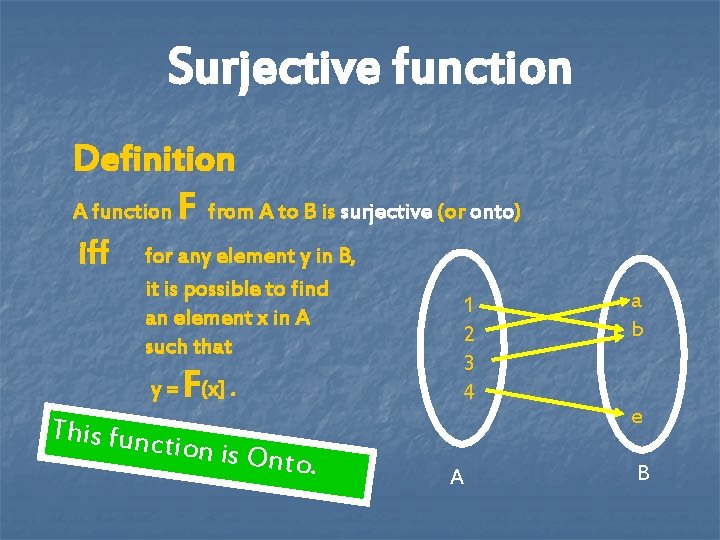
Surjective function Definition A function F from A to B is surjective (or onto) iff for any element y in B, it is possible to find an element x in A such that F y = (x]. This funct ion is Ont o. 1 2 3 4 A a b e B

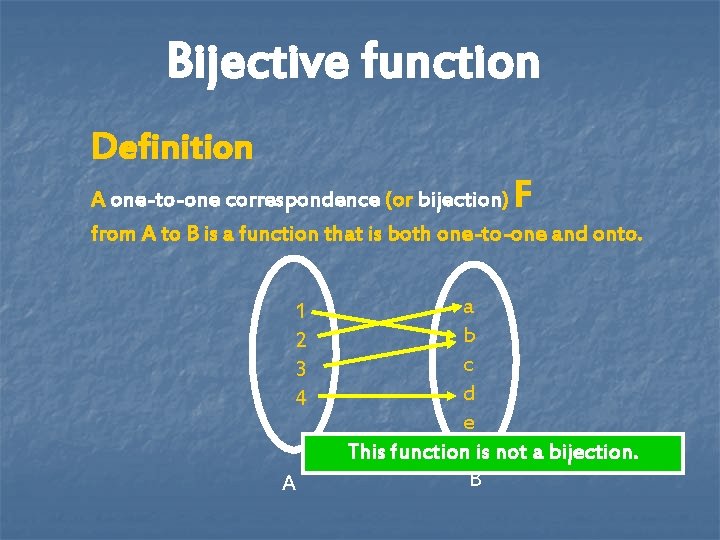
Bijective function Definition F A one-to-one correspondence (or bijection) from A to B is a function that is both one-to-one and onto. 1 2 3 4 A a b c d e This function is not a bijection. B

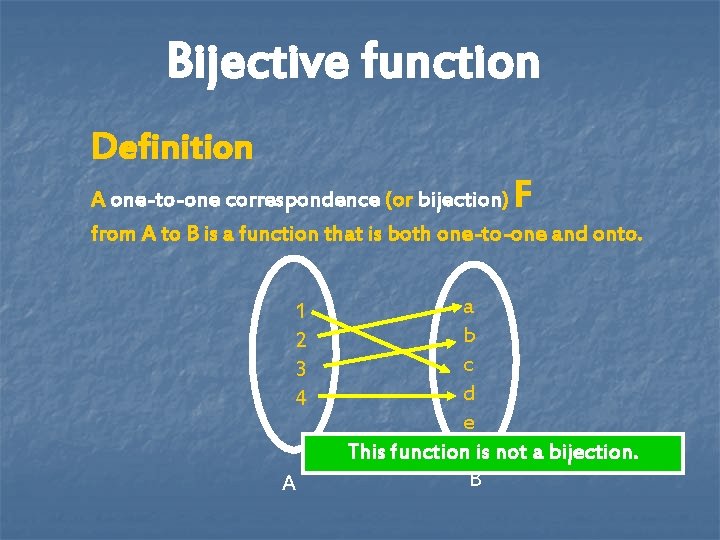
Bijective function Definition F A one-to-one correspondence (or bijection) from A to B is a function that is both one-to-one and onto. 1 2 3 4 A a b c d e This function is not a bijection. B

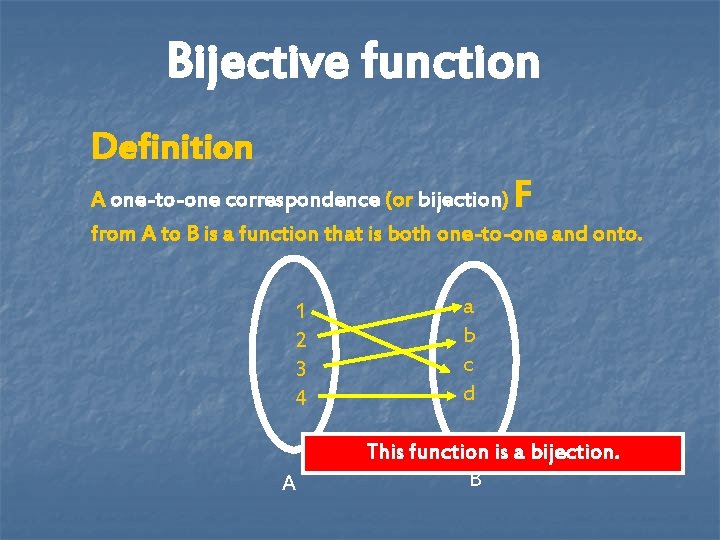
Bijective function Definition F A one-to-one correspondence (or bijection) from A to B is a function that is both one-to-one and onto. 1 2 3 4 A a b c d This function is a bijection. B

Properties Definition Let R be a binary relation on A. R is reflexive iff for all x A, x R x. R is symmetric iff for all x, y A, if x R y then y R x. R is transitive iff for all x, y, z A, if x R y and y R z then x R z.

Equivalence relation Definition R is a equivalence relation on A iff R is a binary relation on A. R is reflexive. R is symmetric. R is transitive.

Transitive closure Definition Let R be a binary relation on A. The transitive closure of R is the binary relation Rt on A That satisfies the following three properties: Rt is transitive. R R t. S is any other transitive that contains R then Rt S.

Mutually disjoint Definition Sets A 1, A 2, A 3, …, An are Mutually disjoint (pairwise or nonoverlapping) Iff, any two sets Ai, Aj with distinct subscripts have not any elements in common, precisely Ai Aj= empty set .

Set partition Definition A collection of nonempty sets {A 1, A 2, A 3, …, An} is a Partition of a set A Iff, A = A 1 A 2 A 3 … An and A 1, A 2, A 3, …, An are mutually disjoint.

Set partition Definition Given a partition of A={A 1, A 2, A 3, …, An}. The binary relation induced by the partition, R, is defined on A as follows: for all x, y A, x R y Iff, there is a subset Aj of the partition such that both x and y are in Aj.

Set partition Theorem Let A be a set with a partition and Let R be the relation induced by the partition. ? m e r o Then R is reflexive, symmetric and transitive. e h t t w Ho s i h t e v o r p o

Equivalence class Definition Suppose A is a set and R is a equivalence relation on A. For each a A, the equivalence class of a, denoted [ a ], is the set of all elements x in A such that x is related to a by R. [ a ] = { x A | x R a }.

Theorem Lemma 1 Let R be an equivalence relation on A, a b A. If a R b then [ a ] = [ b ]. Lemma 2 R be an equivalence relation on A, a b A, then either [ a ] [ b ] = or [ a ] = [ b ]. Theorem If A is a nonempty set and R is an equivalence relation on A, then the distinct equivalence classes of R form a partition of A; that is, Let the union of the equivalence classes is all of A and the intersection of any two distinct classes is empty.

Antisymmetric Definition A relation R on a set A such that (a, b) and (b, a) are in R only if a=b, for all a, b in A, is called antisymmetric.

Example Let R be a relation on the set A R = { (a, b) | a < b } Find the inverse relation R-1 and the complementary relation R.