Discrete Random Variables Section 7 1 1 Starter

Discrete Random Variables Section 7. 1. 1

Starter 7. 1. 1 • Suppose a fair coin is tossed 4 times. Find the probability that heads comes up exactly two times.

Answer • A tree diagram or organized list will show that there are 16 possible outcomes. • The tree diagram also shows that 6 branches contain exactly two heads. • Therefore P(two H) = 6/16 • Another approach: – There are 2 x 2 x 2 x 2=16 outcomes from 4 flips – Choose any two flips to be heads: 4 C 2=6 – So P(two H) = 6/16

Objectives • Write the probability distribution function of a discrete random variable as either a table or a histogram. California Standard 3. 0 Students demonstrate an understanding of the notion of discrete random variables by using this concept to solve for the probabilities of outcomes, such as the probability of the occurrence of five or fewer heads in 14 coin tosses.

Definitions • A random variable is a variable whose value is the numerical outcome of a random event. • A discrete random variable is an r. v. with a countable number of outcomes. • The probability distribution function (PDF) of a discrete r. v. lists all possible outcomes of a random event and the probability of each outcome.

The PDF of 4 Coins • Expand your results from the starter problem to find the probability of each possible outcome when 4 coins are tossed (or one coin is tossed 4 times) – Let X be the number of heads that come up – Think about the possible values of X • What is the greatest number of heads that could come up? • What is the least? • Write your results as an organized table. – It should look like an xy table you might do for an algebraic function.

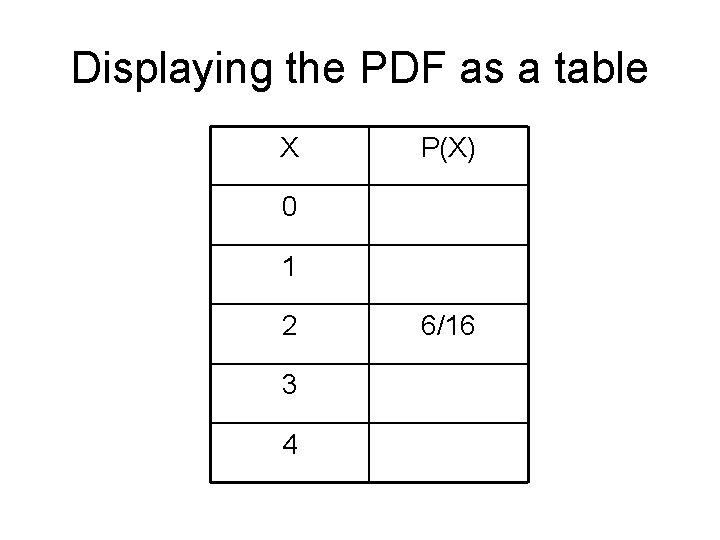
Displaying the PDF as a table X P(X) 0 1 2 3 4 6/16

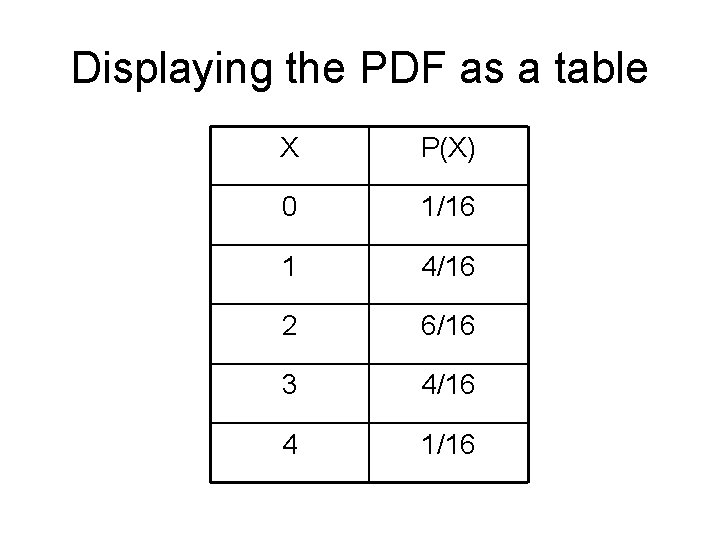
Displaying the PDF as a table X P(X) 0 1/16 1 4/16 2 6/16 3 4/16 4 1/16

Displaying the PDF as a histogram • Draw a histogram of the PDF with outcomes (X values) on the horizontal axis and probabilities on the vertical axis. • What is the total area under the histogram? – The area is exactly 1, so this is a density curve!

Example • Two fair dice are rolled. Let X = the sum. • Write the PDF of X as a table. • Draw the PDF of X as a histogram on paper. – Remember that all axes need labels and scales! X P(X) 2 1/36 3 4 5 6 7 6/36 8 9 10 11 12

Example • Two fair dice are rolled. Let X = the sum. • Write the PDF of X as a table. • Draw the PDF of X as a histogram on paper. – Remember that all axes need labels and scales! • Draw the PDF histogram on your calculator. – X values go in L 1 – P(x) goes in L 2 X P(X) 2 3 4 5 6 7 8 9 10 11 12 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36

Homework • Read pages 367 – 373 • Do problems 1 - 3