Discrete Random Variables Random Variables What We Know

Discrete Random Variables

Random Variables – What We Know n. A random variable is a function that associates a unique numerical value with every outcome of an experiment. n The value of a random variable changes from occurrence to occurrence. n Although we don’t know the next value of a random variable, we do know the overall pattern of the values assumed by a random variable over many repetitions. G. Baker, Department of Statistics University of South Carolina; Slide 2
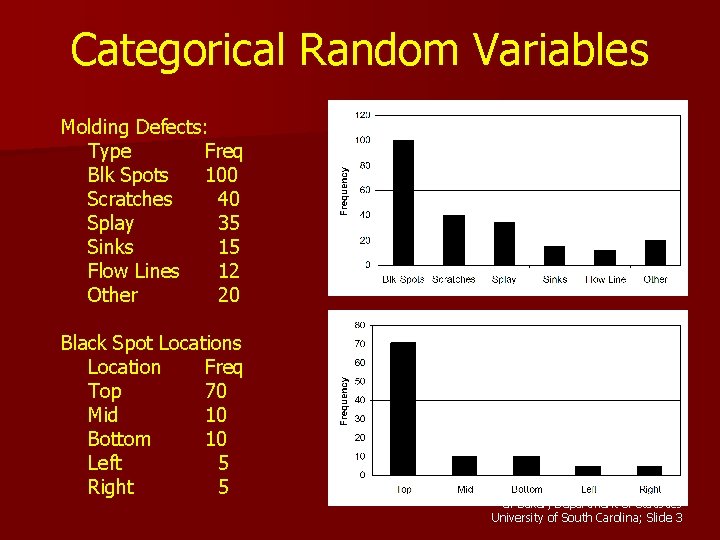
Categorical Random Variables Molding Defects: Type Freq Blk Spots 100 Scratches 40 Splay 35 Sinks 15 Flow Lines 12 Other 20 Black Spot Locations Location Freq Top 70 Mid 10 Bottom 10 Left 5 Right 5 G. Baker, Department of Statistics University of South Carolina; Slide 3

Numerical Random Variables n Assume numerical values from a meaningful numerical scale. n Example: – Age is a numerical variable. – Zip code is a categorical random variable. G. Baker, Department of Statistics University of South Carolina; Slide 4
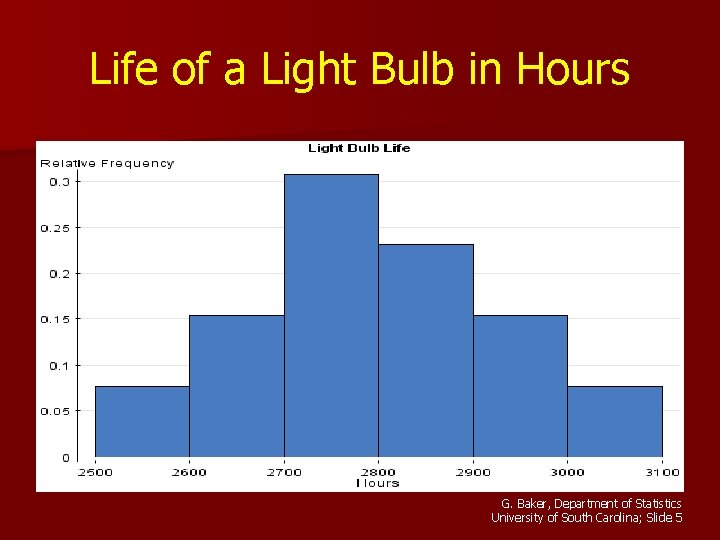
Life of a Light Bulb in Hours G. Baker, Department of Statistics University of South Carolina; Slide 5

Notation n We will use capital letters from the end of the alphabet to represent a random variable. – Usually X or Y n The corresponding lower case letter will represent a particular value of the random variable. – P(Y = y) is the probability that the random variable Y is equal to the value y. G. Baker, Department of Statistics University of South Carolina; Slide 6

Discrete and Continuous Random Variables n. A continuous random variable can take any value in an interval of the real number line. – Usually measurements n. A discrete random variable can take one of a countable list of distinct values. – Usually counts G. Baker, Department of Statistics University of South Carolina; Slide 7
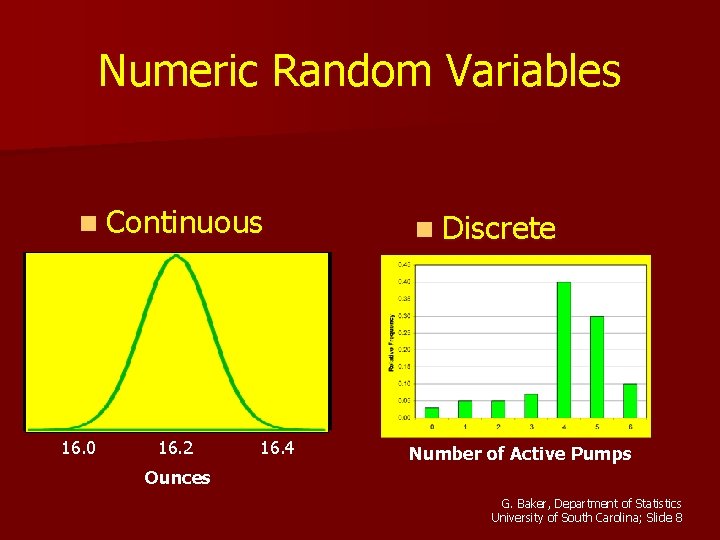
Numeric Random Variables n Continuous 16. 0 16. 2 16. 4 n Discrete Number of Active Pumps Ounces G. Baker, Department of Statistics University of South Carolina; Slide 8

Discrete and Continuous Random Variables n Discrete or continuous? – Time until a projectile returns to earth. – The number of times a transistor in computer memory changes state in one operation. – The volume of gasoline that is lost to evaporation during the filling of a gas tank. – The outside diameter of a machined shaft. – The number of chapters in your text book. G. Baker, Department of Statistics University of South Carolina; Slide 9

Discrete Numeric Random Variables n A small airport in New Zealand is interested in the number of late aircraft arrivals per day. Every day for a year it counts the daily number of late arrivals. Let random variable Y = Number of aircraft in one day that arrive late. Y 0 1 2 3 P(Y=y) 0. 12 0. 19 0. 30 0. 26 4+ 0. 13 G. Baker, Department of Statistics University of South Carolina; Slide 10

Discrete Numeric Random Variables Y P(Y=y) 0 0. 12 1 0. 19 2 0. 30 3 0. 26 4+ 0. 13 n What is the probability that on any randomly chosen day that 3 aircraft are late? n What is the chance that on any randomly chosen day at least 1 aircraft is late? G. Baker, Department of Statistics University of South Carolina; Slide 11

Discrete Numeric Random Variables n An assembly consists of three mechanical components. Suppose that the probabilities that the first, second, and third components meet specifications are 0. 90, 0. 95 and 0. 99 respectively. Assume the components are independent. n Let Si = the event that a component is within specification. G. Baker, Department of Statistics University of South Carolina; Slide 12

Possible Outcomes for One assembly S 1 S 2 S 3 S 1 S 2 S 3 0. 84645 0. 00095 0. 00495 0. 00855 0. 04455 0. 09405 0. 00005 Let Y = Number of components within specification in a randomly chosen assembly Y 0 1 P(Y=y) 0. 00005 0. 00635 2 0. 14715 3 0. 84645 G. Baker, Department of Statistics University of South Carolina; Slide 13

Discrete Random Variables n Probability or Distribution Function p(y) = P(Y = y) Note: 0 < p(y) < 1 for every value of y and G. Baker, Department of Statistics University of South Carolina; Slide 14
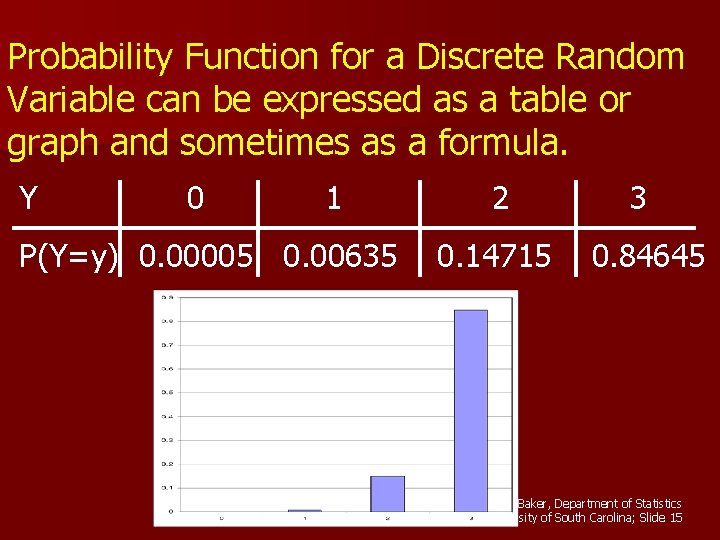
Probability Function for a Discrete Random Variable can be expressed as a table or graph and sometimes as a formula. Y 0 1 P(Y=y) 0. 00005 0. 00635 2 0. 14715 3 0. 84645 G. Baker, Department of Statistics University of South Carolina; Slide 15

Cumulative Probability or Distribution Function n If Y is a random variable, then the cumulative distribution function is denoted by F(y). n F(y) = P(Y < y) G. Baker, Department of Statistics University of South Carolina; Slide 16

Number of Components within Specification for a Randomly chosen Assembly Distribution Function: Y 0 1 P(Y=y) 0. 00005 0. 00635 2 0. 14715 3 0. 84645 Cumulative Distribution Function: Y 0 1 P(Y<y) 0. 00005 0. 00640 2 3 0. 15355 1. 0000 G. Baker, Department of Statistics University of South Carolina; Slide 17
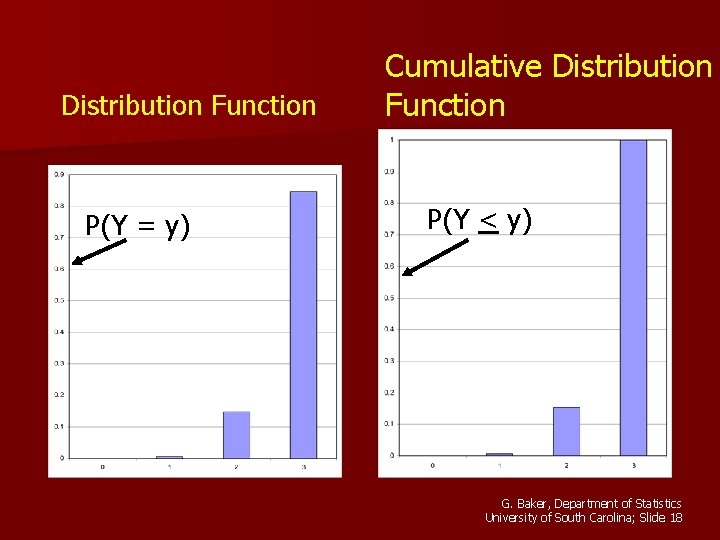
Distribution Function P(Y = y) Cumulative Distribution Function P(Y < y) G. Baker, Department of Statistics University of South Carolina; Slide 18

Expected Value n Note, this distribution is the distribution for a population Y 0 1 P(Y=y) 0. 00005 0. 00635 2 0. 14715 3 0. 84645 n The expected value of the population is the population mean, µ, for the distribution. G. Baker, Department of Statistics University of South Carolina; Slide 19
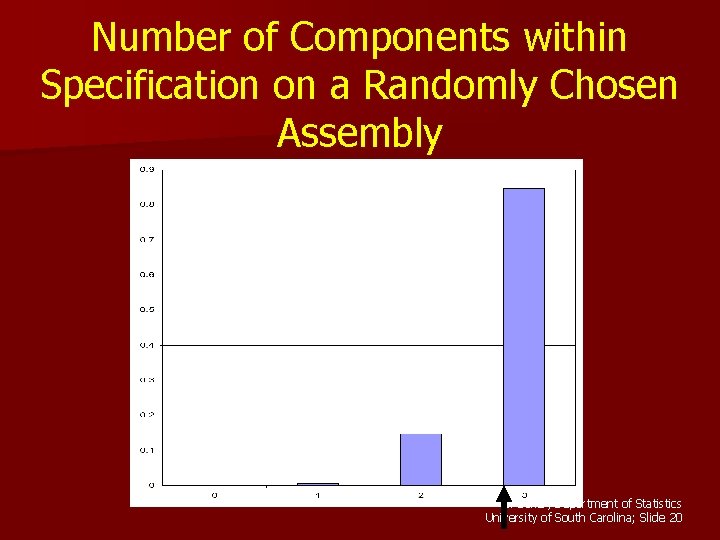
Number of Components within Specification on a Randomly Chosen Assembly G. Baker, Department of Statistics University of South Carolina; Slide 20

Variance Y 0 1 P(Y=y) 0. 00005 0. 00635 2 0. 14715 3 0. 84645 n The variance of the population is the expected value of (Y - µ)2. G. Baker, Department of Statistics University of South Carolina; Slide 21

Computational Formula for Variance G. Baker, Department of Statistics University of South Carolina; Slide 22

Population Standard Deviation is the positive square root of the variance. G. Baker, Department of Statistics University of South Carolina; Slide 23

We receive 75% of a certain part from Supplier A and 25% from supplier B. Two of these parts are used in an assembly. Let Y = number of parts from Supplier A in the assembly. What is the expected value of Y? G. Baker, Department of Statistics University of South Carolina; Slide 24

A project manager for an engineering firm submitted bids on three projects. The following table summarizes the firm’s chances of having the three projects accepted. Project A Prob of accept 0. 30 B 0. 80 C 0. 10 Assuming the projects are independent of one another, what is the probability that the firm will have all three projects accepted? G. Baker, Department of Statistics University of South Carolina; Slide 25

What is the probability of having at least one project accepted? Project A Prob of accept 0. 30 B 0. 80 C 0. 10 G. Baker, Department of Statistics University of South Carolina; Slide 26

Let Y = number of projects accepted. y 0 1 p(y) 0. 126 0. 572 2 3 0. 278 0. 024 What is the expected number of projects accepted? G. Baker, Department of Statistics University of South Carolina; Slide 27

Let Y = number of projects accepted. y 0 1 p(y) 0. 126 0. 572 2 3 0. 278 0. 024 What is the variance for number of projects accepted? G. Baker, Department of Statistics University of South Carolina; Slide 28

Rules of Expectation 1) E(c) = c 2) E(c. Y) = c. E(Y) 3) E(X + Y) = E(X) + E(Y) G. Baker, Department of Statistics University of South Carolina; Slide 29
Consider the following process: 1 5 1 G. Baker, Department of Statistics University of South Carolina; Slide 30

Rules of Variance 1) Var(c) = 0 2) Var(c. Y) = c 2 Var(Y) 3) Var(X + Y) = Var(X) + Var(Y) G. Baker, Department of Statistics University of South Carolina; Slide 31

Binomial Random Variable n Suppose we toss a fair coin 20 times, counting the number of heads. n This is an example of a binomial experiment. n The possible outcomes can be represented with a binomial random variable which follows a binomial distribution. G. Baker, Department of Statistics University of South Carolina; Slide 32

Binomial Experiment Y represents the outcome of n identical trials. 2) There are two possible outcomes for each trial: success and failure. 3) Outcomes are independent from trial to trial. 4) Probability of success, p, remains constant from trial to trial. 1) G. Baker, Department of Statistics University of South Carolina; Slide 33

Binomial Experiment n Each toss of the coin is a trail. We performed 20 trials. So n = 20. n The two possible outcomes of a trials are heads or tails. Since we are counting heads, heads is a success, while tails is a failure. n Are the outcomes of our trials independent of one another? n Probability of success (heads) is 0. 50 G. Baker, Department of Statistics University of South Carolina; Slide 34

Binomial Experiment n n n n A manufacturer of water filters for refrigerators monitors the process for defective filters. Historically, this process averages 5% defective filters. Suppose five filters are randomly selected for testing and we count number of defective filters. Define a trial. Calculate n. Define a “success”. Are the outcomes independent from trial to trial? Calculate p. G. Baker, Department of Statistics University of South Carolina; Slide 35

Water Filters n. A manufacturer of water filters for refrigerators monitors the process for defective filters. Historically, this process averages 5% defective filters. Five filters are randomly selected. n Find the probability that all five filters are defective. n Find the probability that no filters are defective. n Find the probability that exactly 1 filter is defective. G. Baker, Department of Statistics University of South Carolina; Slide 36

n. A manufacturer of water filters for refrigerators monitors the process for defective filters. Historically, this process averages 5% defective filters. Five filters are randomly selected. n Find the probability that exactly 2 filters are defective. A. 5(. 05)2(. 95)3 B. 10(. 05)2(. 95)3 C. 15(. 05)2(. 95)3 G. Baker, Department of Statistics University of South Carolina; Slide 37

Remember Combinations n Number of ways to choose r distinct objects from n distinct objects: “n choose r” G. Baker, Department of Statistics University of South Carolina; Slide 38

Probability Function for a Binomial Random Variable for y = 0, 1, 2, …, n G. Baker, Department of Statistics University of South Carolina; Slide 39

If Y follows a Binomial Distribution n Binomial mean n Binomial variance n Binomial standard deviation G. Baker, Department of Statistics University of South Carolina; Slide 40
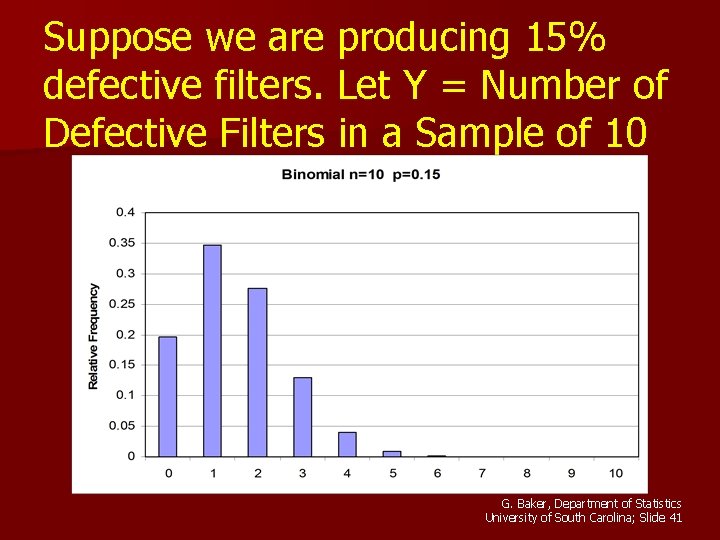
Suppose we are producing 15% defective filters. Let Y = Number of Defective Filters in a Sample of 10 G. Baker, Department of Statistics University of South Carolina; Slide 41
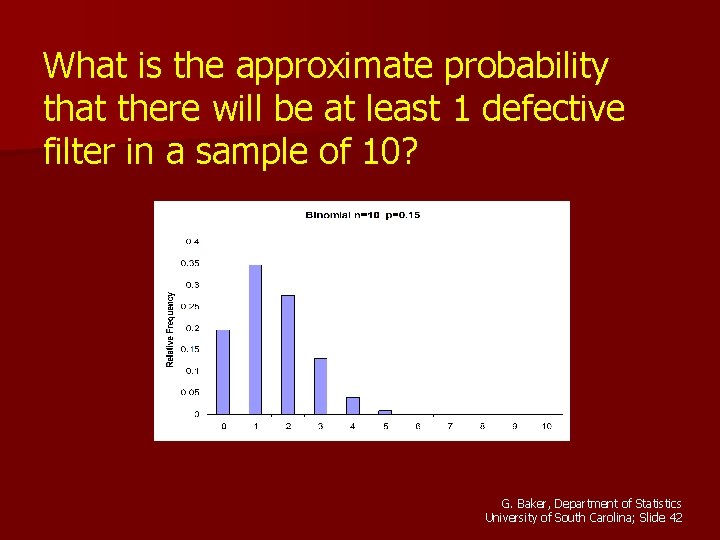
What is the approximate probability that there will be at least 1 defective filter in a sample of 10? G. Baker, Department of Statistics University of South Carolina; Slide 42

Historically, 10% of homes in Florida have radon levels higher than that recommended by the EPA. In a random sample of 20 homes, find the probability that exactly 3 have radon levels higher than the EPA recommendation. Assume home are independent of one another. G. Baker, Department of Statistics University of South Carolina; Slide 43

If a manufacturing process has a 0. 03 defective rate, what is the probability that at least one of the next 25 units inspected will be defective? A. (0. 03)1 * (0. 97)24 B. 1– (0. 03)1 * (0. 97)24 C. 1– (0. 03)0 * (0. 97)25 D. 1– (0. 03)25 G. Baker, Department of Statistics University of South Carolina; Slide 44

A manufacturing process has a 0. 03 defective rate. If we randomly sample 25 units What is the probability that less than 6 will be defective? b) What is the probability that 4 or more are defective? c) What is the probability that between 2 and 5, inclusive, are defective? a) G. Baker, Department of Statistics University of South Carolina; Slide 45

Golf Resort n At a particular golf resort, if a person hits a hole-in-one, the player gets to select 4 slips of paper from a bin of 100 slips. Of the 100 slips of paper, 2 are good for a brand new driver valued at $300. So if the person selects 1 or 2 slips good for the driver, he gets the driver. n Is this a binomial experiment? n We can get the answer using straight probability. G. Baker, Department of Statistics University of South Carolina; Slide 46

Golf Resort n Let Y = number of slips chosen that are good for a free driver. n To win, the player must draw 1 or 2 of the 2 slips which entitle him to a free driver. n P(Y = 1 or 2) = P(Y = 1) + P(Y = 2) n Recall: G. Baker, Department of Statistics University of South Carolina; Slide 47

Probability of Winning Driver G. Baker, Department of Statistics University of South Carolina; Slide 48

Hypergeometric Distribution n Models the number of successes out of n trials when sampling without replacement from a finite population of N objects that contains exactly r successes. for y = 0, 1, 2, …, n G. Baker, Department of Statistics University of South Carolina; Slide 49

Hypergeometric Distribution n Expected Value: G. Baker, Department of Statistics University of South Carolina; Slide 50

If a shipment of 100 generators contains 5 faulty generators, what is the probability that we can select 10 generators from the shipment and not get a faulty one? A B C D G. Baker, Department of Statistics University of South Carolina; Slide 51

Insulated Wire n Consider a process that produces insulated copper wire. Historically the process has averaged 2. 6 breaks in the insulation per 1000 meters of wire. We want to find the probability that 1000 meters of wire will have 1 or fewer breaks in insulation? n Is this a binomial problem? n A hypergeometric problem? G. Baker, Department of Statistics University of South Carolina; Slide 52

Poisson Distribution n Poisson distribution can be used to model the number of events occurring in a continuous time or space. n Let Y = number of breaks in 1000 meters of wire. n P(Y < 1) = P(Y = 0) + P(Y = 1) G. Baker, Department of Statistics University of South Carolina; Slide 53

Poisson Distribution for y = 0, 1, 2, … where λ is the average number of occurrences per base unit. and t is the number of base units inspected. Further: G. Baker, Department of Statistics University of South Carolina; Slide 54

Insulated Wire Let Y = Number of breaks in 1000 meters of wire. λ = 2. 6 and t = 1 The expected number of breaks in 1000 meters of wire is 2. 6. G. Baker, Department of Statistics University of South Carolina; Slide 55

Insulated Wire n If we were inspecting 2000 meters of wire, λt = 2. 6*2 = 5. 2 n If we were inspecting 500 meters of wire, λt = 2. 6*0. 5 = 1. 3 G. Baker, Department of Statistics University of South Carolina; Slide 56

Conditions for a Poisson Distribution Areas of inspection are independent of one another. 2) The probability of the event occurring at any particular point in space or time is negligible. 3) The mean remains constant over all areas of inspection. 1) G. Baker, Department of Statistics University of South Carolina; Slide 57

Suppose we average 5 radioactive particles passing a counter in 1 millisecond. What is the probability that exactly 3 particles will pass in one millisecond? G. Baker, Department of Statistics University of South Carolina; Slide 58

Suppose we average 5 radioactive particles passing a counter in 1 millisecond. What is the probability that exactly 10 particles will pass in three milliseconds? G. Baker, Department of Statistics University of South Carolina; Slide 59
- Slides: 59