Discrete Optimization MA 2827 Fondements de loptimisation discrte

Discrete Optimization MA 2827 Fondements de l’optimisation discrète https: //project. inria. fr/2015 ma 2827/ Slides courtesy of M. Pawan Kumar

Outline • Preliminaries – Functions and Excess Functions – s-t Flow – s-t Cut – Flows vs. Cuts • Maximum Flow • Algorithms

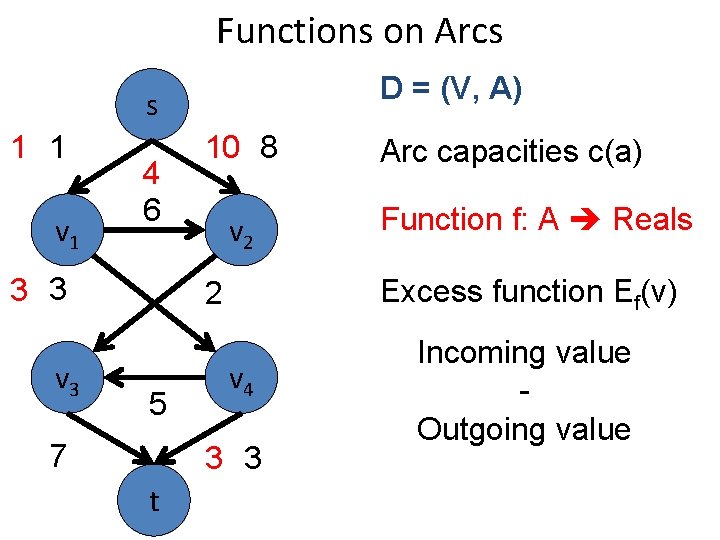
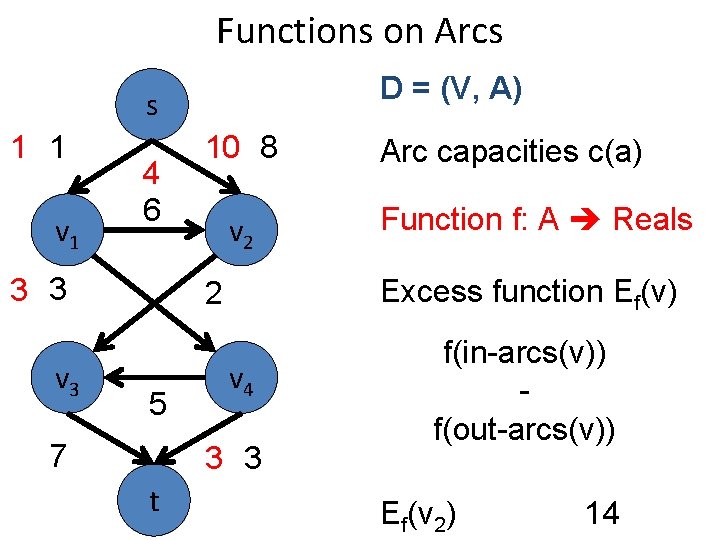
Functions on Arcs D = (V, A) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 7 v 4 3 3 t Function f: A Reals Excess function Ef(v) 2 5 Arc capacities c(a) Incoming value Outgoing value

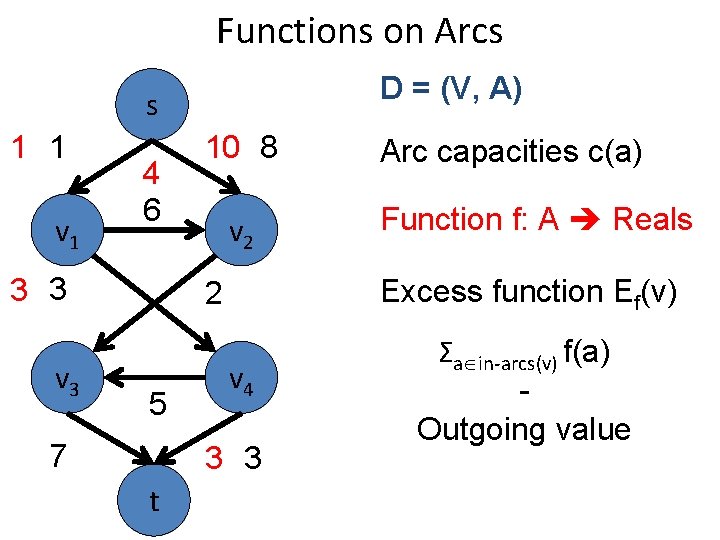
Functions on Arcs D = (V, A) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 7 v 4 3 3 t Function f: A Reals Excess function Ef(v) 2 5 Arc capacities c(a) Σa in-arcs(v) f(a) Outgoing value

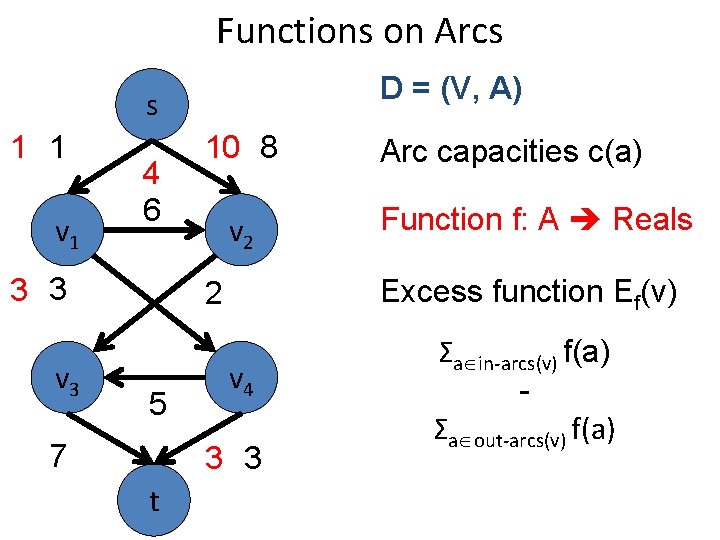
Functions on Arcs D = (V, A) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 7 v 4 3 3 t Function f: A Reals Excess function Ef(v) 2 5 Arc capacities c(a) Σa in-arcs(v) f(a) Σa out-arcs(v) f(a)

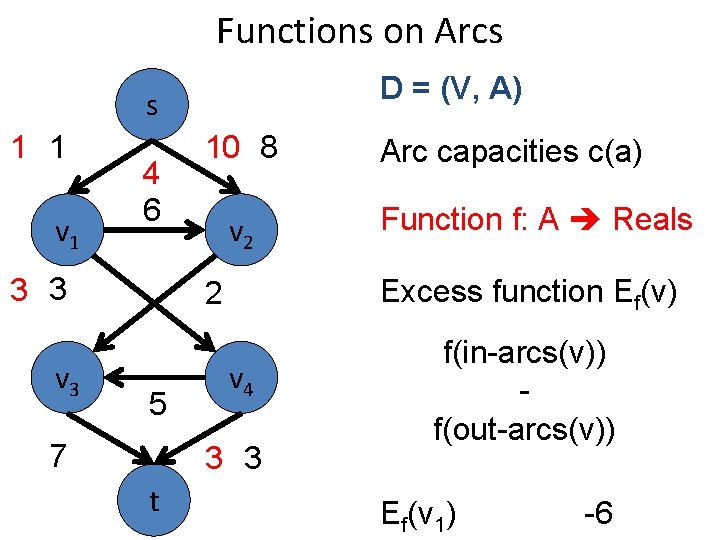
Functions on Arcs D = (V, A) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 7 v 4 3 3 t Function f: A Reals Excess function Ef(v) 2 5 Arc capacities c(a) f(in-arcs(v)) f(out-arcs(v)) Ef(v 1) -6

Functions on Arcs D = (V, A) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 7 v 4 3 3 t Function f: A Reals Excess function Ef(v) 2 5 Arc capacities c(a) f(in-arcs(v)) f(out-arcs(v)) Ef(v 2) 14

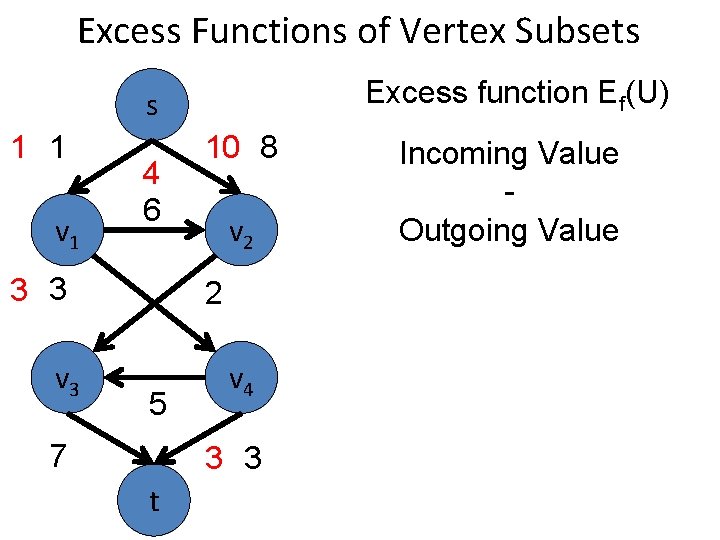
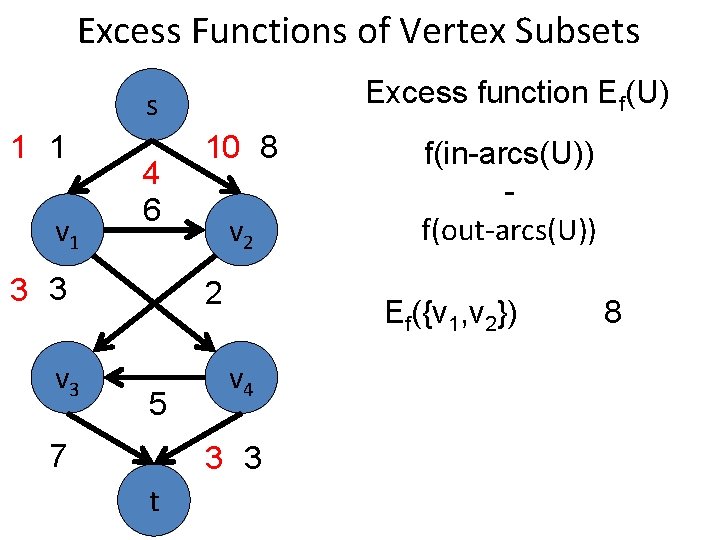
Excess Functions of Vertex Subsets Excess function Ef(U) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 2 5 7 v 4 3 3 t Incoming Value Outgoing Value

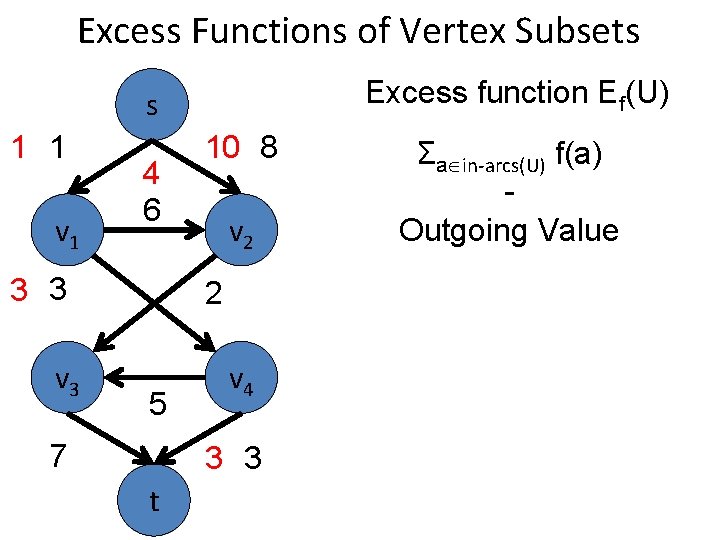
Excess Functions of Vertex Subsets Excess function Ef(U) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 2 5 7 v 4 3 3 t Σa in-arcs(U) f(a) Outgoing Value

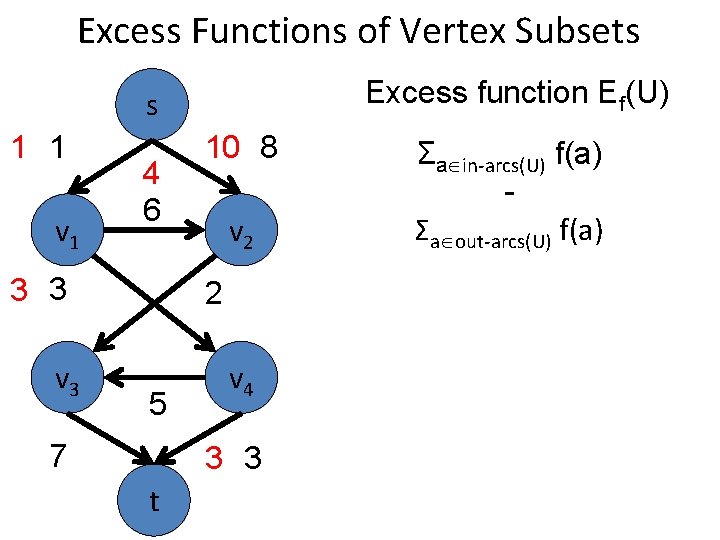
Excess Functions of Vertex Subsets Excess function Ef(U) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 2 5 7 v 4 3 3 t Σa in-arcs(U) f(a) Σa out-arcs(U) f(a)

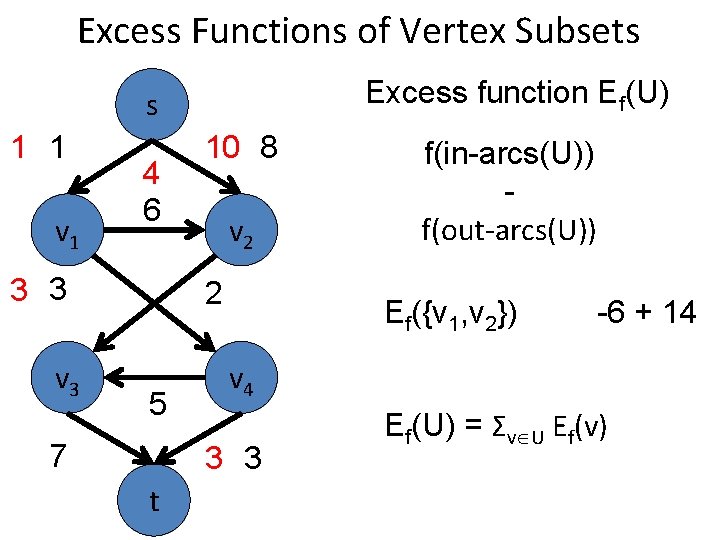
Excess Functions of Vertex Subsets Excess function Ef(U) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 2 5 7 Ef({v 1, v 2}) v 4 3 3 t f(in-arcs(U)) f(out-arcs(U)) 8

Excess Functions of Vertex Subsets Excess function Ef(U) s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 2 5 7 Ef({v 1, v 2}) -6 + 14 v 4 3 3 t f(in-arcs(U)) f(out-arcs(U)) Ef(U) = Σv U Ef(v)

Outline • Preliminaries – Functions and Excess Functions – s-t Flow – s-t Cut – Flows vs. Cuts • Maximum Flow • Algorithms

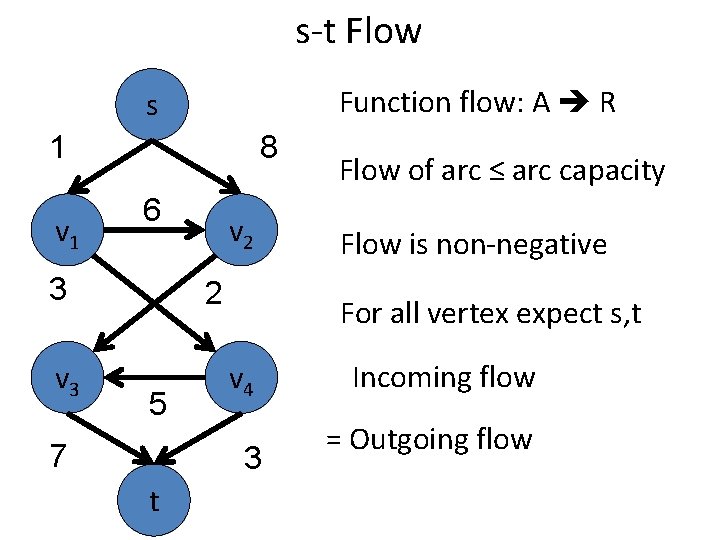
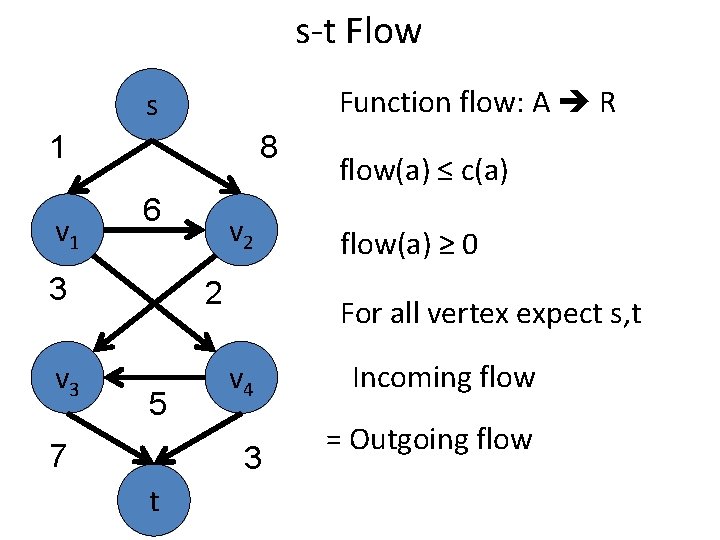
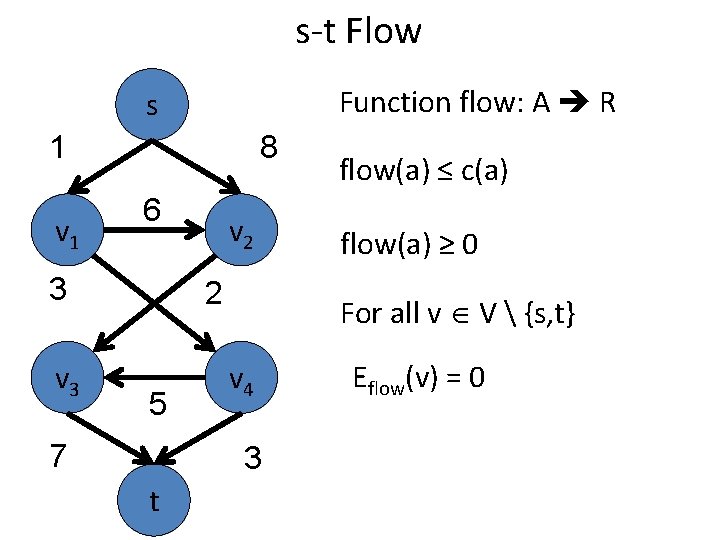
s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 Flow is non-negative For all vertex expect s, t v 4 3 t Flow of arc ≤ arc capacity Incoming flow = Outgoing flow

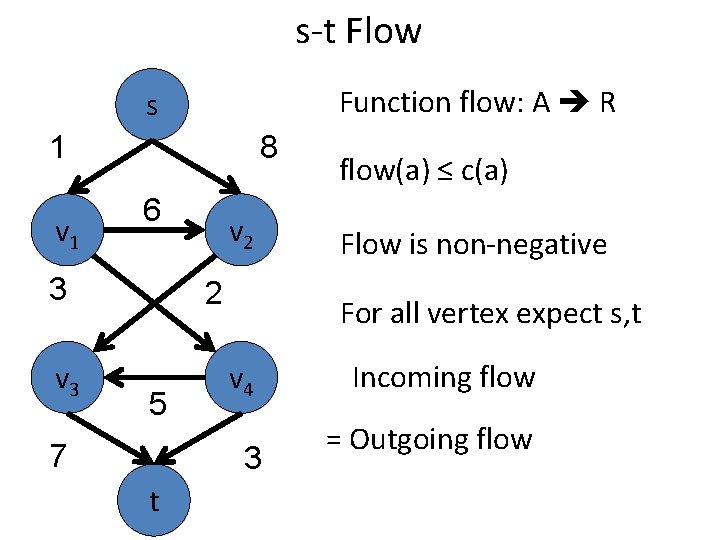
s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 Flow is non-negative For all vertex expect s, t v 4 3 t flow(a) ≤ c(a) Incoming flow = Outgoing flow

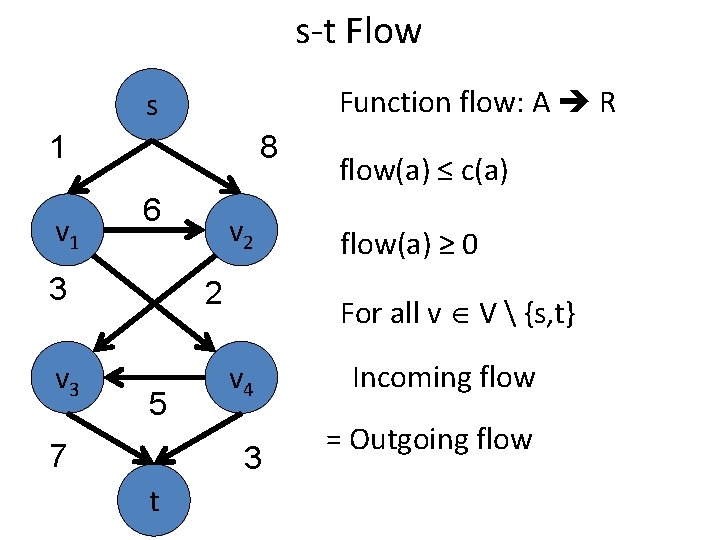
s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 flow(a) ≥ 0 For all vertex expect s, t v 4 3 t flow(a) ≤ c(a) Incoming flow = Outgoing flow

s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 flow(a) ≥ 0 For all v V {s, t} v 4 3 t flow(a) ≤ c(a) Incoming flow = Outgoing flow

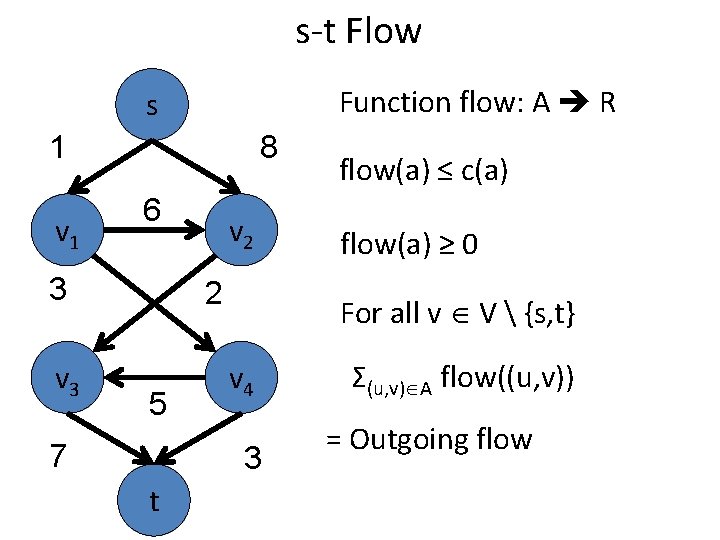
s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 flow(a) ≥ 0 For all v V {s, t} v 4 3 t flow(a) ≤ c(a) Σ(u, v) A flow((u, v)) = Outgoing flow

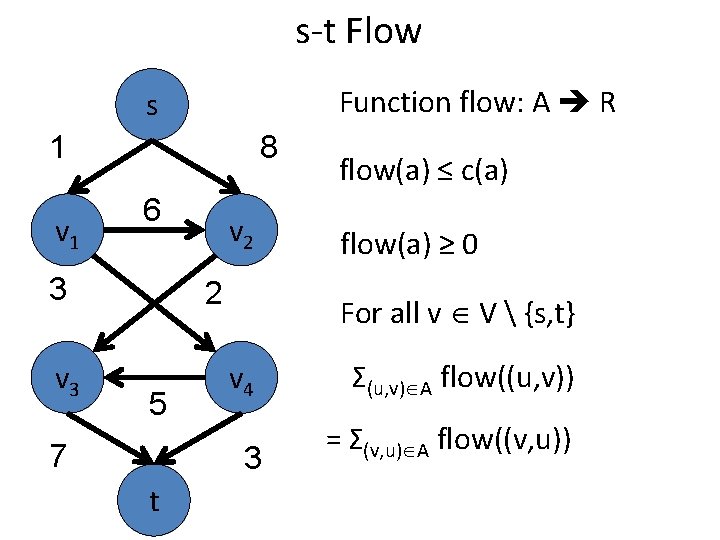
s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 t flow(a) ≤ c(a) flow(a) ≥ 0 For all v V {s, t} v 4 Σ(u, v) A flow((u, v)) 3 = Σ(v, u) A flow((v, u))

s-t Flow Function flow: A R s 1 v 1 8 6 3 v 2 2 5 7 flow(a) ≥ 0 For all v V {s, t} v 4 3 t flow(a) ≤ c(a) Eflow(v) = 0

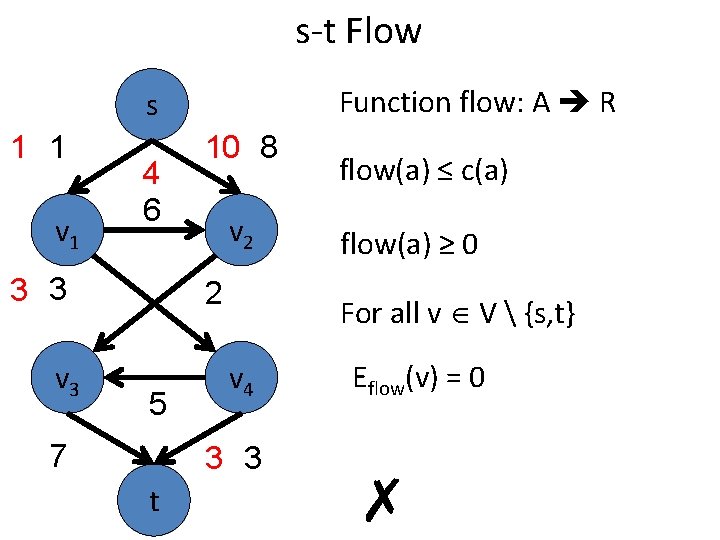
s-t Flow Function flow: A R s 1 1 v 1 4 6 3 3 v 3 10 8 v 2 2 5 7 flow(a) ≥ 0 For all v V {s, t} v 4 3 3 t flow(a) ≤ c(a) Eflow(v) = 0 ✗

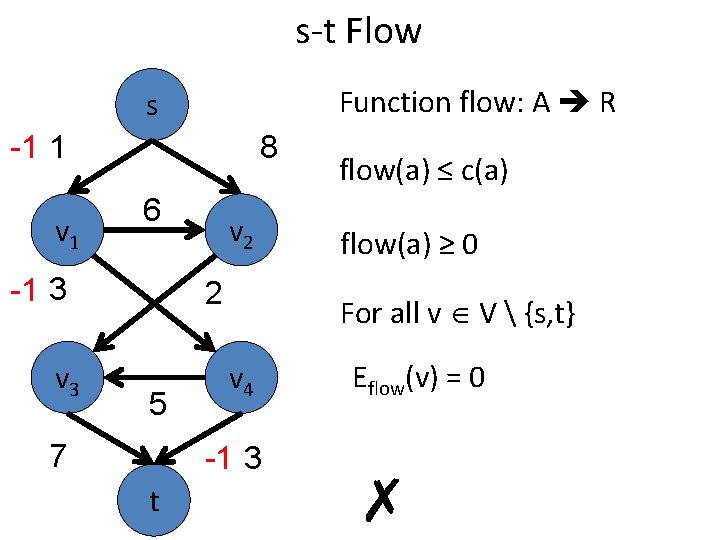
s-t Flow Function flow: A R s -1 1 v 1 8 6 -1 3 v 2 2 5 7 flow(a) ≥ 0 For all v V {s, t} v 4 -1 3 t flow(a) ≤ c(a) Eflow(v) = 0 ✗

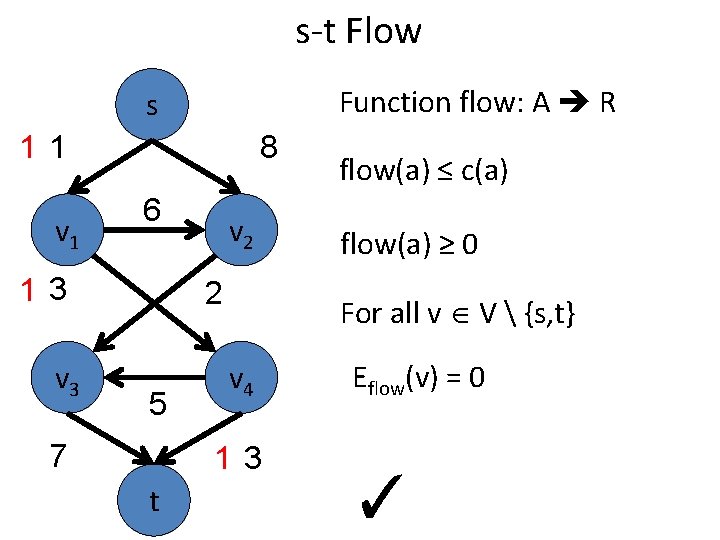
s-t Flow Function flow: A R s 11 v 1 8 6 13 v 2 2 5 7 flow(a) ≥ 0 For all v V {s, t} v 4 13 t flow(a) ≤ c(a) Eflow(v) = 0 ✓

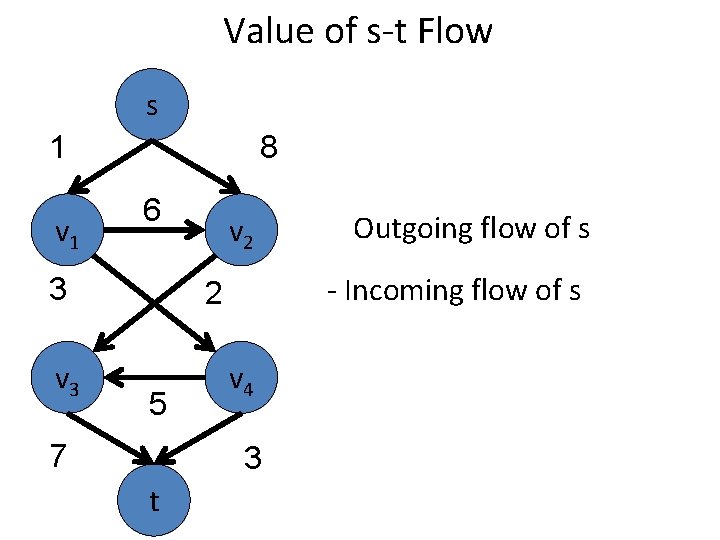
Value of s-t Flow s 1 v 1 8 6 3 v 2 - Incoming flow of s 2 5 7 v 4 3 t Outgoing flow of s

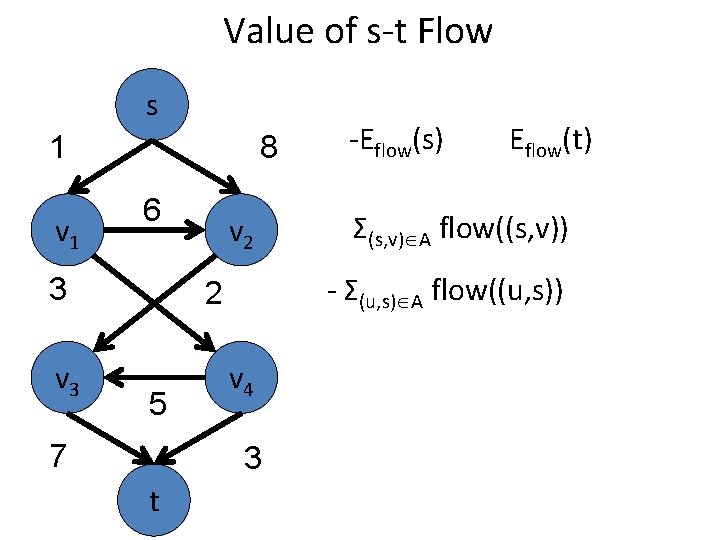
Value of s-t Flow s 1 v 1 8 6 3 v 2 7 v 4 3 t Eflow(t) Σ(s, v) A flow((s, v)) - Σ(u, s) A flow((u, s)) 2 5 -Eflow(s)

Value of s-t Flow s 11 v 1 8 6 13 v 2 7 v 4 13 t Eflow(t) Σ(s, v) A flow((s, v)) - Σ(u, s) A flow((u, s)) 2 5 -Eflow(s) Value = 1

Outline • Preliminaries – Functions and Excess Functions – s-t Flow – s-t Cut – Flows vs. Cuts • Maximum Flow • Algorithms

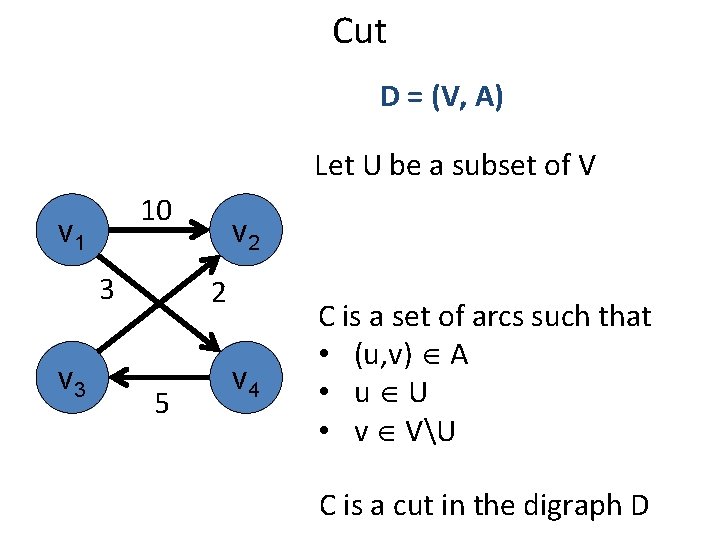
Cut D = (V, A) Let U be a subset of V 10 v 1 3 v 2 2 5 v 4 C is a set of arcs such that • (u, v) A • u U • v VU C is a cut in the digraph D

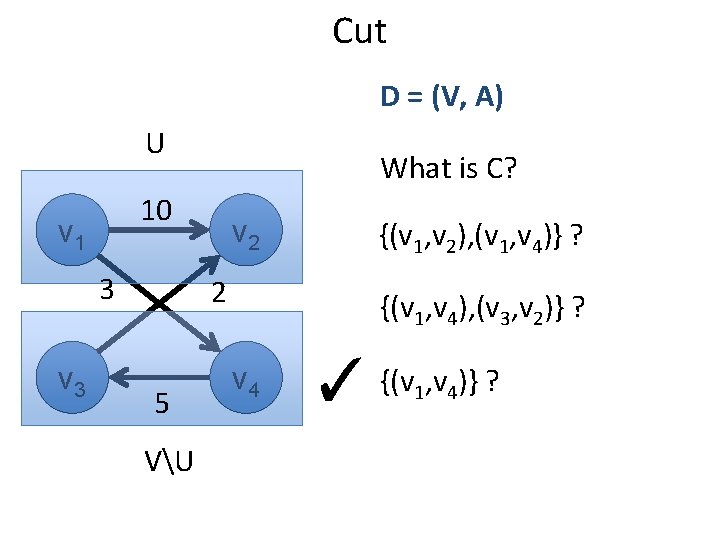
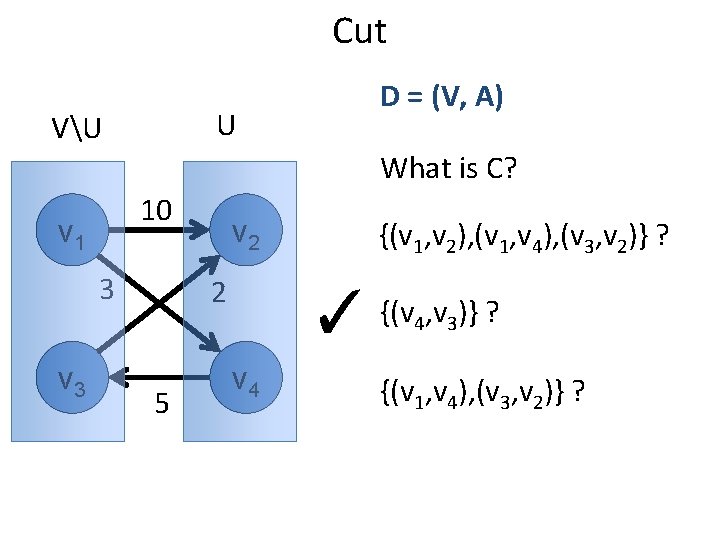
Cut D = (V, A) U 10 v 1 3 v 3 What is C? v 2 2 5 VU {(v 1, v 2), (v 1, v 4)} ? {(v 1, v 4), (v 3, v 2)} ? v 4 ✓ {(v , v )} ? 1 4

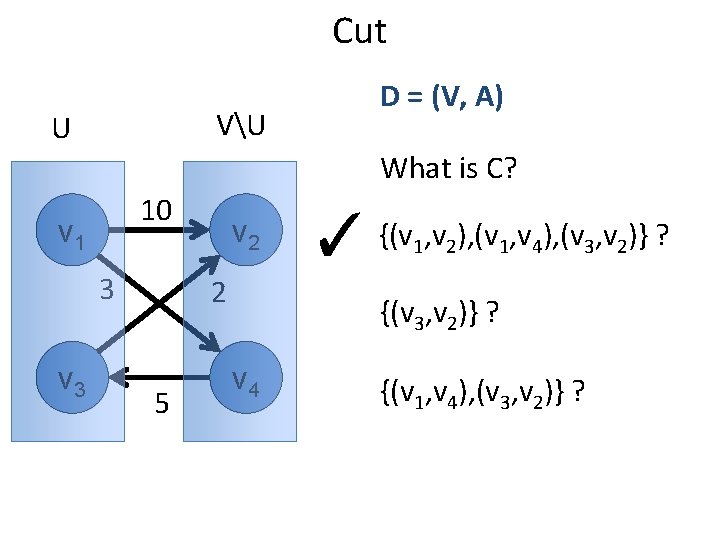
Cut U VU D = (V, A) What is C? 10 v 1 3 v 2 2 5 {(v 1, v 2), (v 1, v 4), (v 3, v 2)} ? ✓ {(v , v )} ? 4 v 4 3 {(v 1, v 4), (v 3, v 2)} ?

Cut VU U D = (V, A) What is C? 10 v 1 3 v 2 2 5 ✓ {(v , v ), (v , v )} ? 1 2 1 4 3 {(v 3, v 2)} ? v 4 {(v 1, v 4), (v 3, v 2)} ? 2

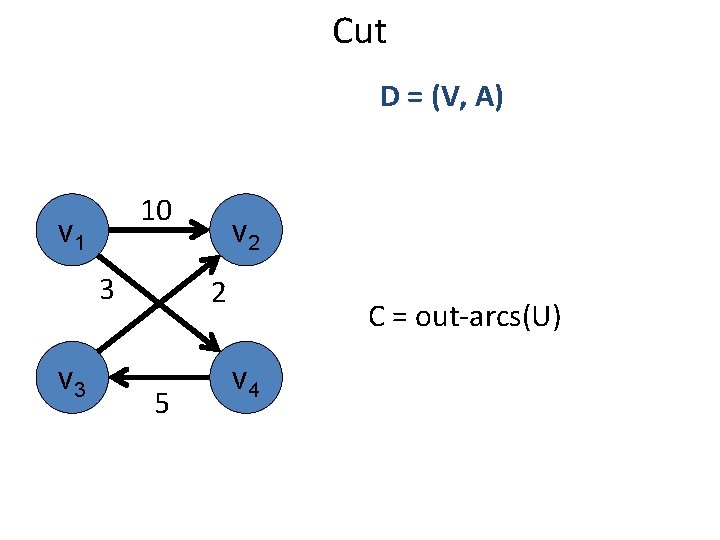
Cut D = (V, A) 10 v 1 3 v 2 2 5 C = out-arcs(U) v 4

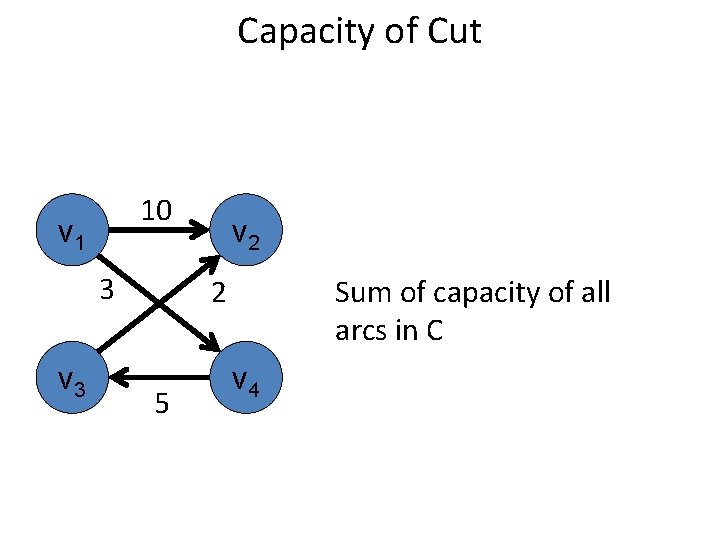
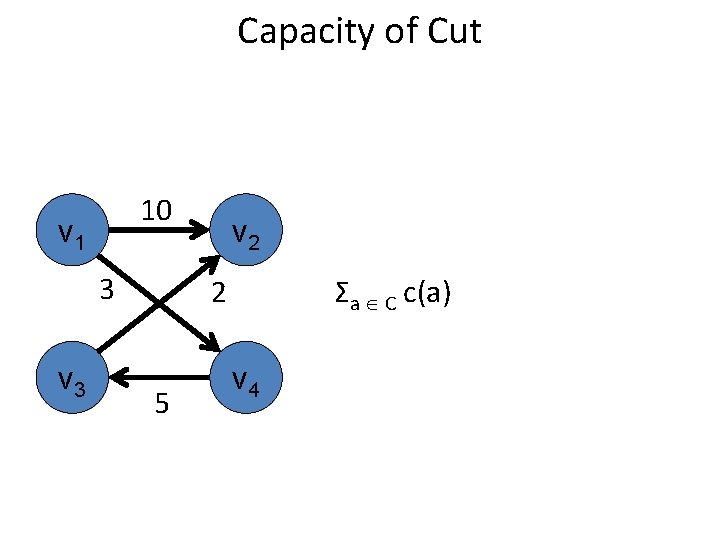
Capacity of Cut 10 v 1 3 v 2 Sum of capacity of all arcs in C 2 5 v 4

Capacity of Cut 10 v 1 3 v 2 Σa C c(a) 2 5 v 4

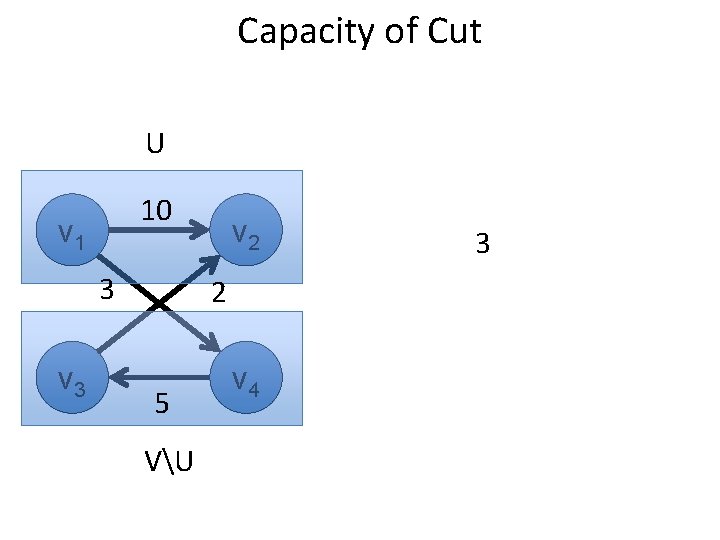
Capacity of Cut U 10 v 1 3 v 2 2 5 VU v 4 3

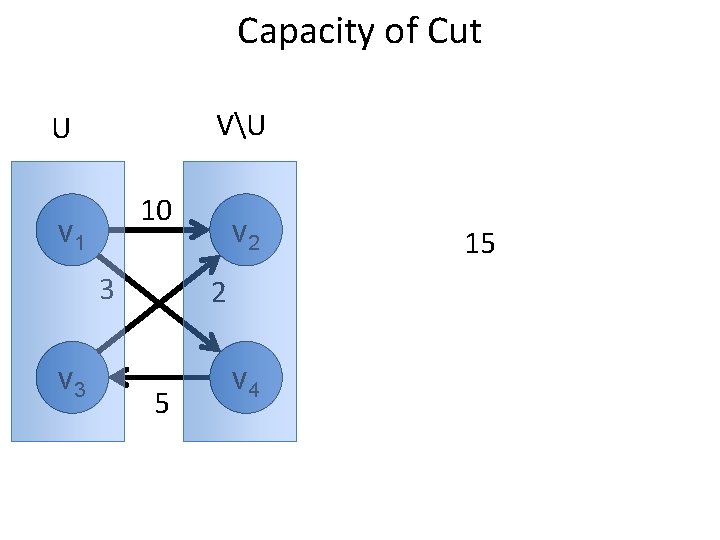
Capacity of Cut VU U 10 v 1 3 v 2 2 5 v 4 15

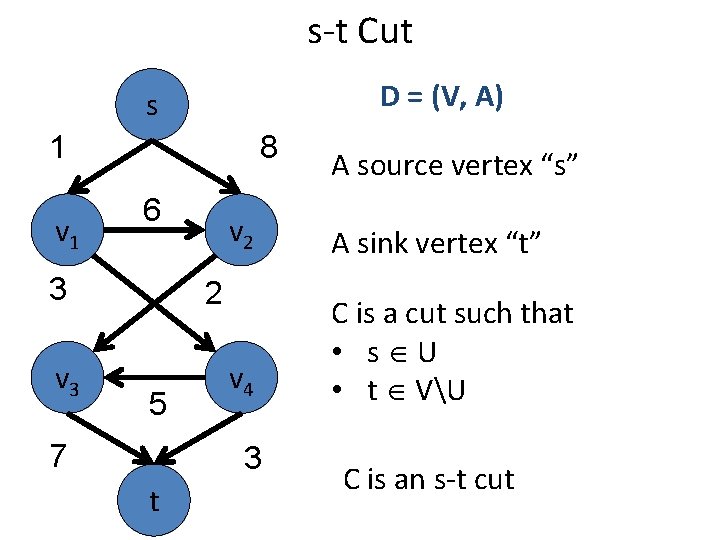
s-t Cut D = (V, A) s 1 v 1 8 6 3 v 2 A sink vertex “t” v 4 C is a cut such that • s U • t VU 2 5 7 3 t A source vertex “s” C is an s-t cut

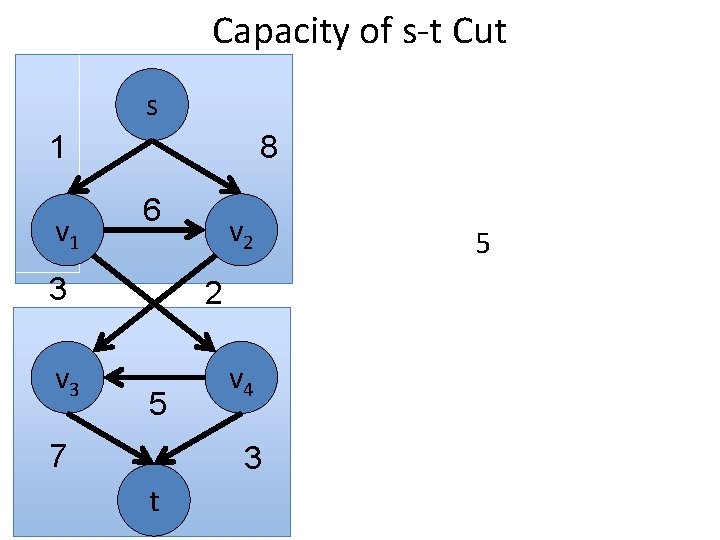
Capacity of s-t Cut s 1 v 1 8 6 3 v 2 2 5 7 v 4 3 t Σa C c(a)

Capacity of s-t Cut s 1 v 1 8 6 3 v 2 2 5 7 v 4 3 t 5

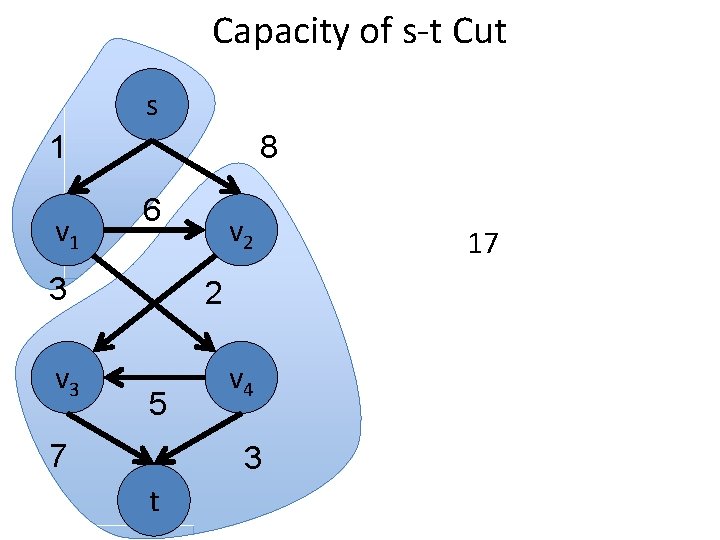
Capacity of s-t Cut s 1 v 1 8 6 3 v 2 2 5 7 v 4 3 t 17

Outline • Preliminaries – Functions and Excess Functions – s-t Flow – s-t Cut – Flows vs. Cuts • Maximum Flow • Algorithms

Flows vs. Cuts An s-t flow function flow: A Reals An s-t cut C such that s U, t VU Value of flow ≤ Capacity of C

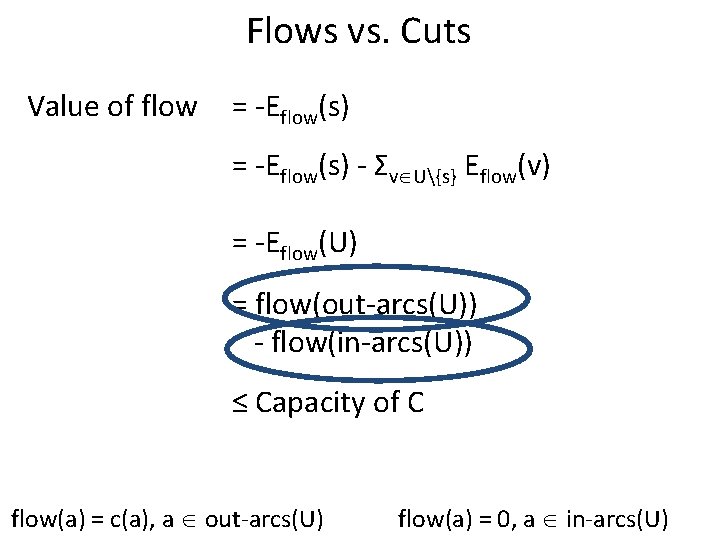
Flows vs. Cuts Value of flow = -Eflow(s) - Σv U{s} Eflow(v) = -Eflow(U) = flow(out-arcs(U)) - flow(in-arcs(U)) ≤ Capacity of C - flow(in-arcs(U))

Flows vs. Cuts Value of flow = -Eflow(s) - Σv U{s} Eflow(v) = -Eflow(U) = flow(out-arcs(U)) - flow(in-arcs(U)) ≤ Capacity of C When does equality hold?

Flows vs. Cuts Value of flow = -Eflow(s) - Σv U{s} Eflow(v) = -Eflow(U) = flow(out-arcs(U)) - flow(in-arcs(U)) ≤ Capacity of C flow(a) = c(a), a out-arcs(U) flow(a) = 0, a in-arcs(U)

Flows vs. Cuts Value of flow = -Eflow(s) - Σv U{s} Eflow(v) = -Eflow(U) = flow(out-arcs(U)) - flow(in-arcs(U)) = Capacity of C flow(a) = c(a), a out-arcs(U) flow(a) = 0, a in-arcs(U)

Outline • Preliminaries • Maximum Flow – Residual Graph – Max-Flow Min-Cut Theorem • Algorithms

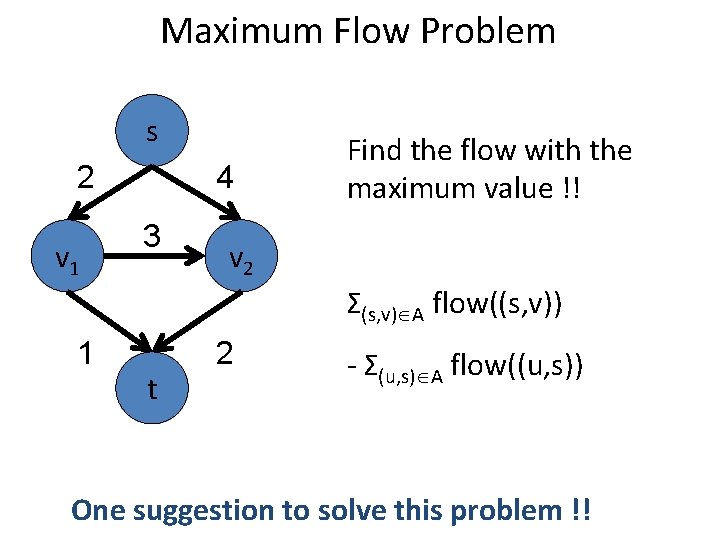
Maximum Flow Problem s 2 v 1 4 3 Find the flow with the maximum value !! v 2 Σ(s, v) A flow((s, v)) 1 t 2 - Σ(u, s) A flow((u, s)) One suggestion to solve this problem !!

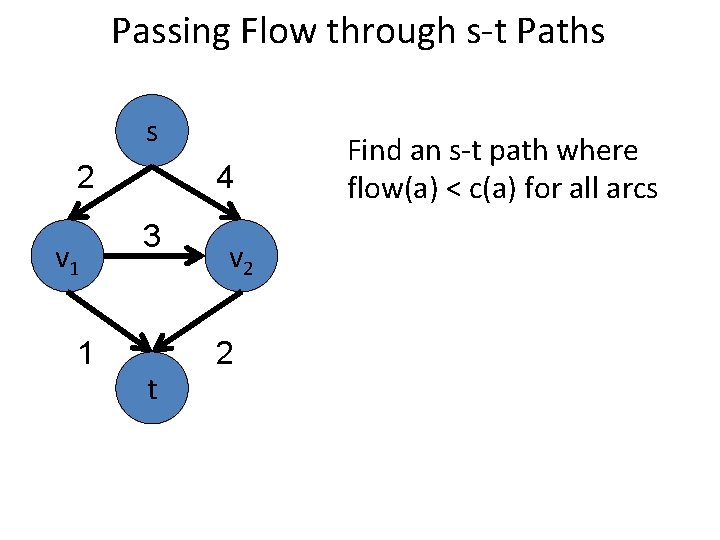
Passing Flow through s-t Paths s 2 v 1 1 4 3 t v 2 2 Find an s-t path where flow(a) < c(a) for all arcs

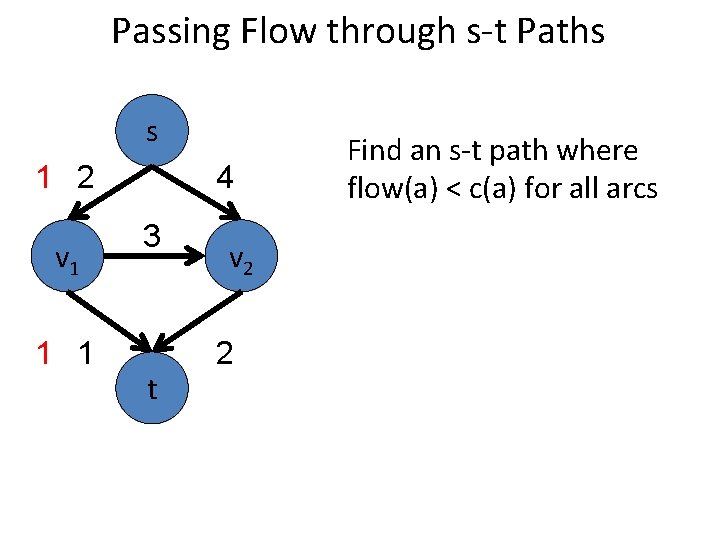
Passing Flow through s-t Paths s 1 2 v 1 1 1 4 3 t Find an s-t path where flow(a) < c(a) for all arcs v 2 2 Pass maximum allowable flow through the arcs

Passing Flow through s-t Paths s 1 2 v 1 1 1 4 3 t v 2 2 Find an s-t path where flow(a) < c(a) for all arcs

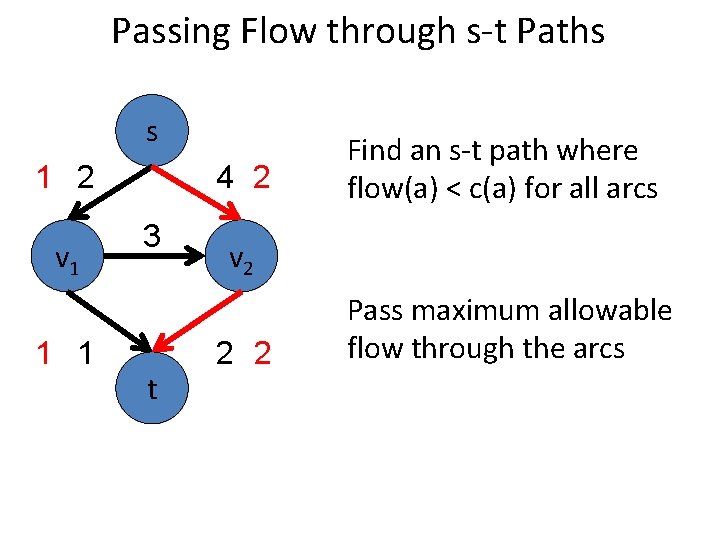
Passing Flow through s-t Paths s 1 2 v 1 1 1 4 2 3 t Find an s-t path where flow(a) < c(a) for all arcs v 2 2 2 Pass maximum allowable flow through the arcs

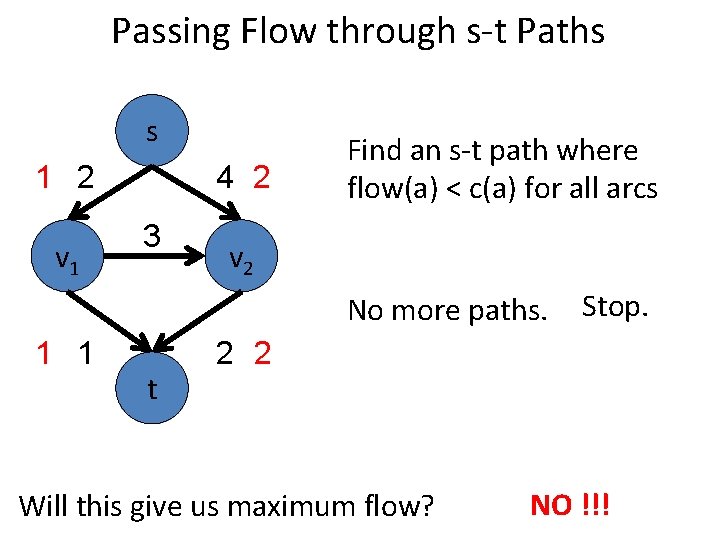
Passing Flow through s-t Paths s 1 2 v 1 4 2 3 Find an s-t path where flow(a) < c(a) for all arcs v 2 No more paths. 1 1 t Stop. 2 2 Will this give us maximum flow? NO !!!

Passing Flow through s-t Paths s 2 2 v 1 1 2 3 t 4 Find an s-t path where flow(a) < c(a) for all arcs v 2 2 2 Pass maximum allowable flow through the arcs

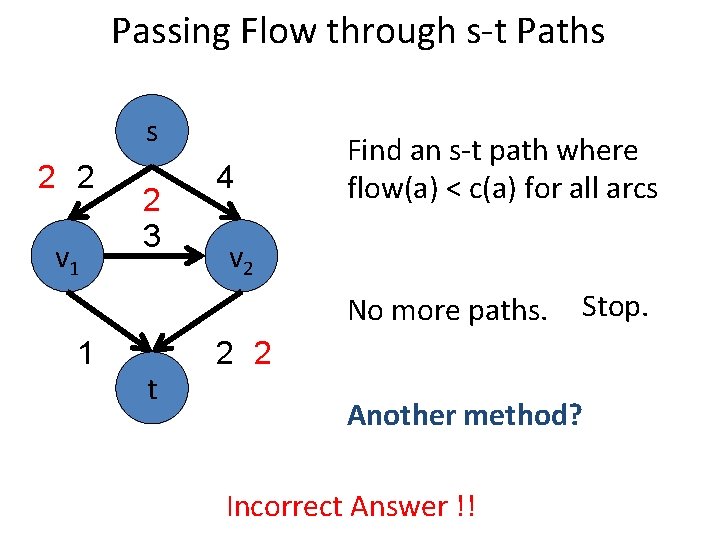
Passing Flow through s-t Paths s 2 2 v 1 2 3 4 Find an s-t path where flow(a) < c(a) for all arcs v 2 No more paths. 1 t Stop. 2 2 Another method? Incorrect Answer !!

Outline • Preliminaries • Maximum Flow – Residual Graph – Max-Flow Min-Cut Theorem • Algorithms

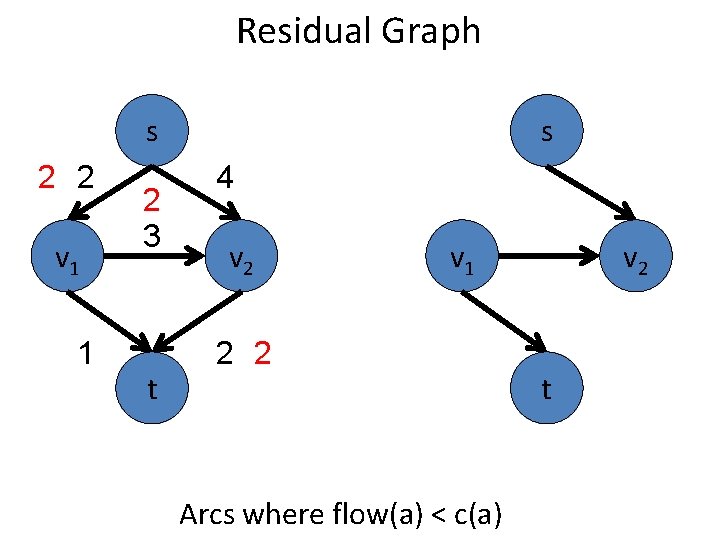
Residual Graph s 2 2 v 1 1 2 3 t s 4 v 2 v 1 2 2 Arcs where flow(a) < c(a) v 2 t

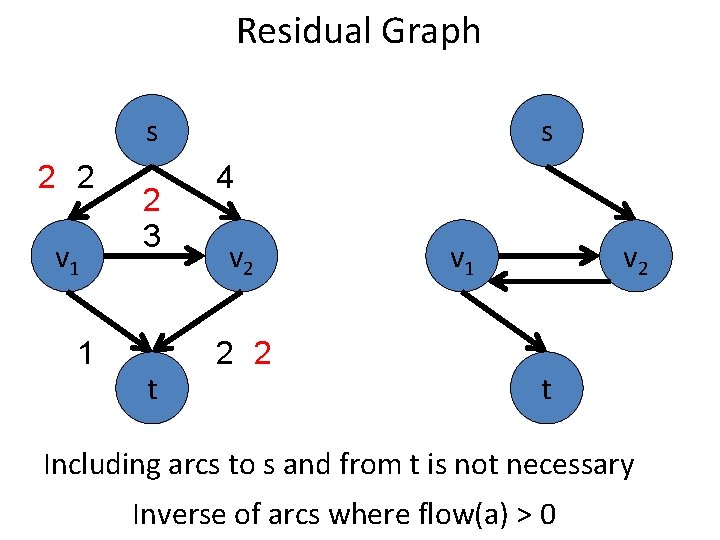
Residual Graph s 2 2 v 1 1 2 3 t s 4 v 2 2 2 v 1 v 2 t Including arcs to s and from t is not necessary Inverse of arcs where flow(a) > 0

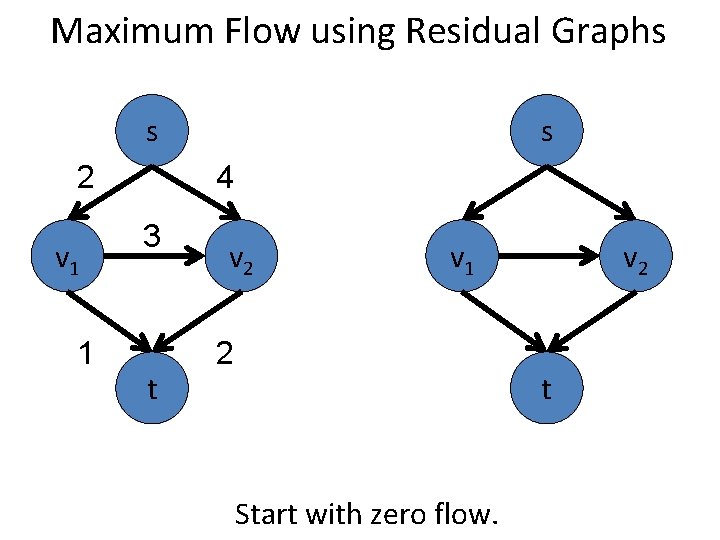
Maximum Flow using Residual Graphs s 2 v 1 1 s 4 3 t v 2 v 1 2 v 2 t Start with zero flow.

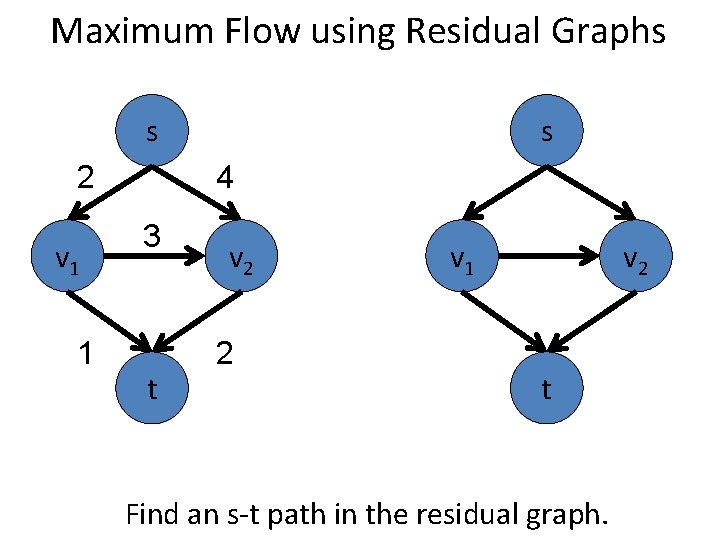
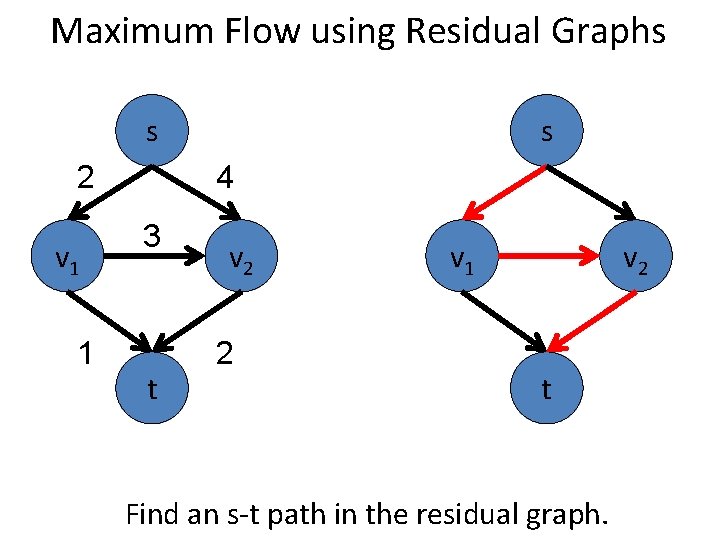
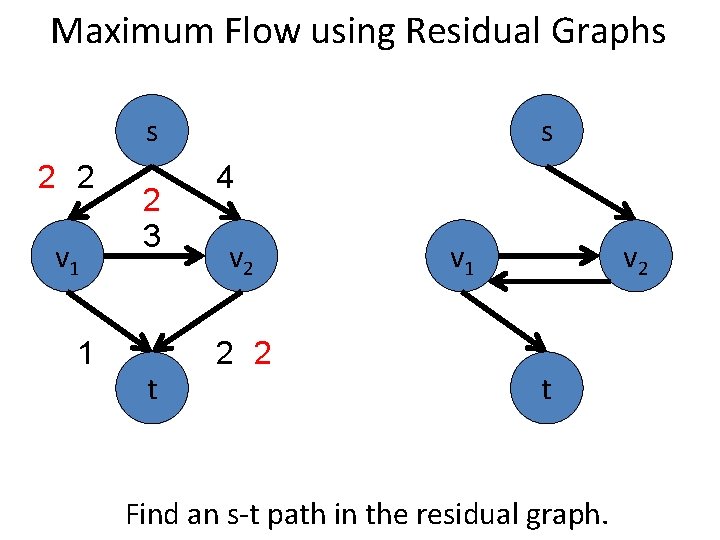
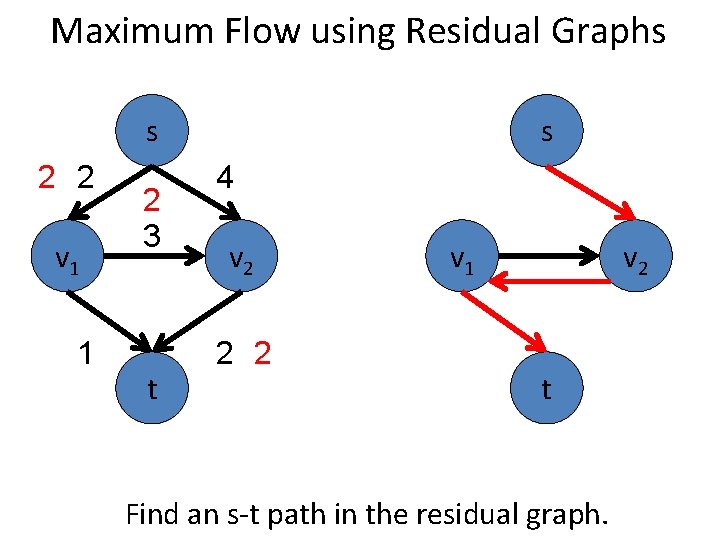
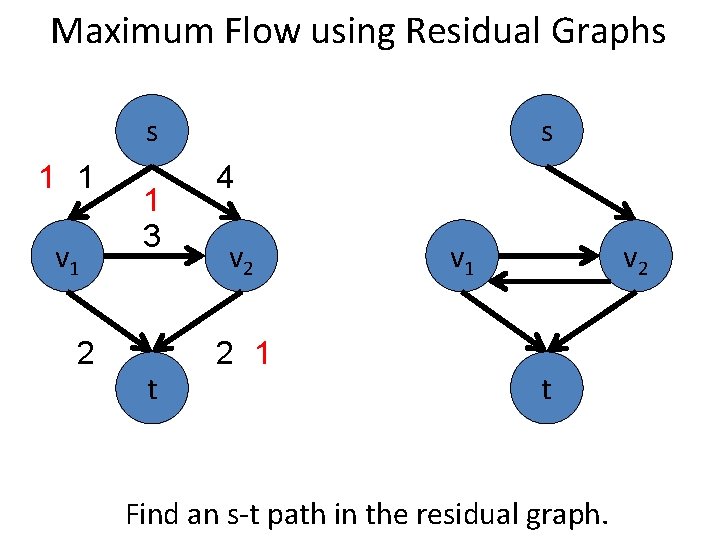
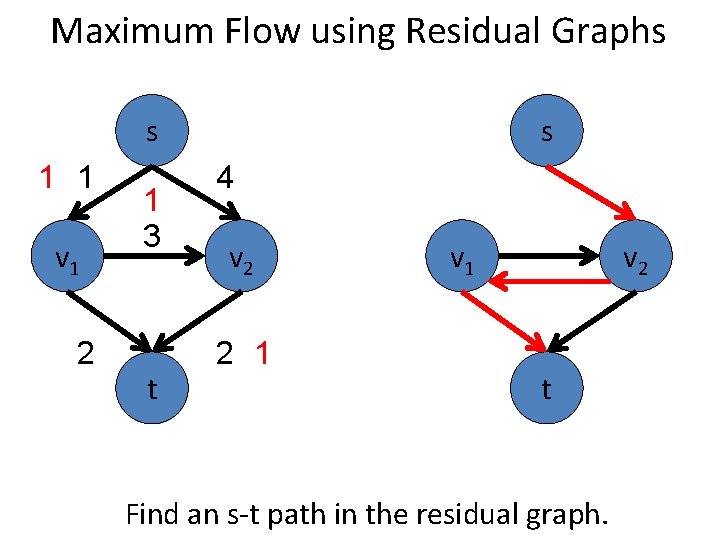
Maximum Flow using Residual Graphs s 2 v 1 1 s 4 3 t v 2 2 v 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 2 v 1 1 s 4 3 t v 2 2 v 1 v 2 t Find an s-t path in the residual graph.

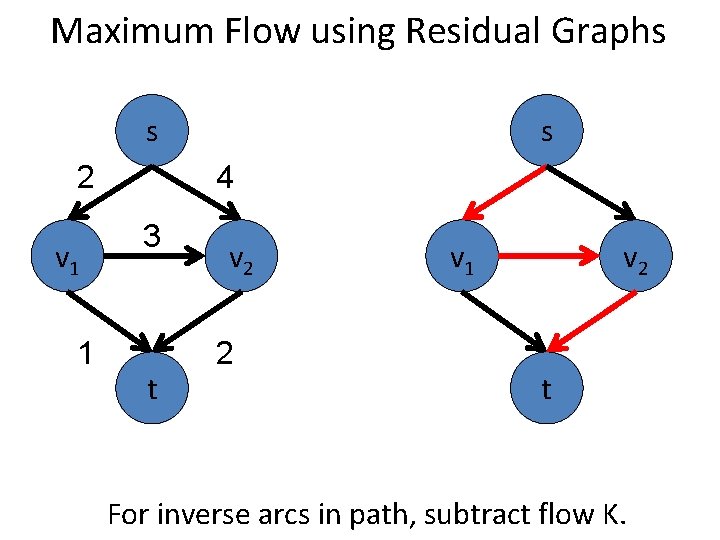
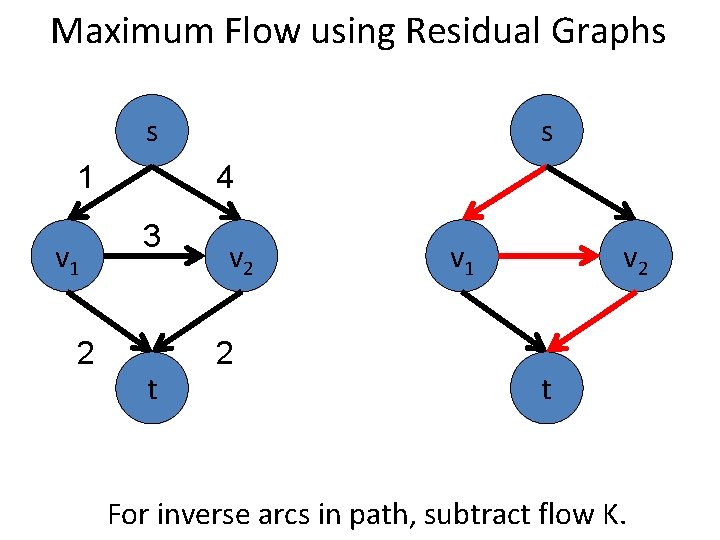
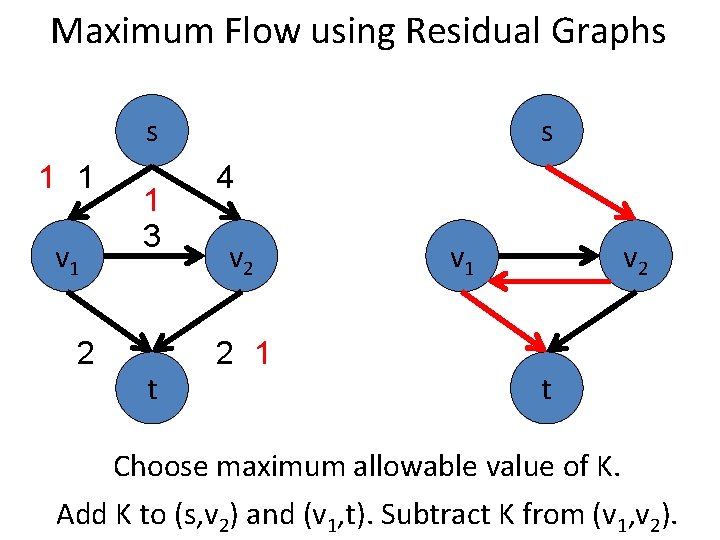
Maximum Flow using Residual Graphs s 2 v 1 1 s 4 3 t v 2 2 v 1 v 2 t For inverse arcs in path, subtract flow K.

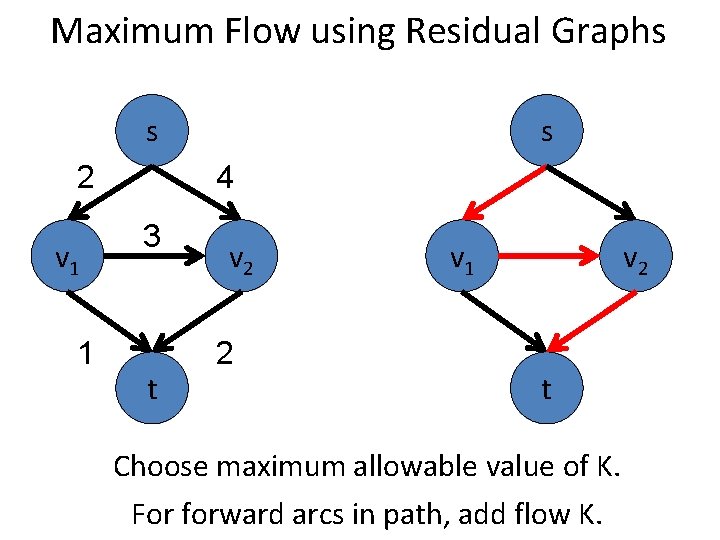
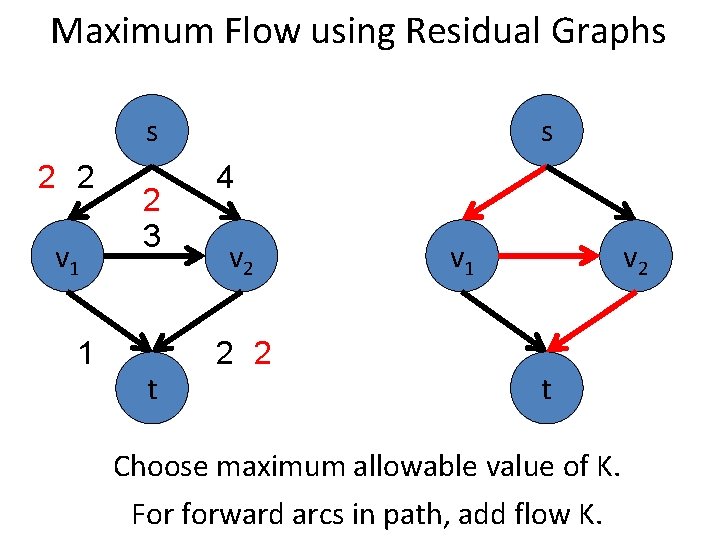
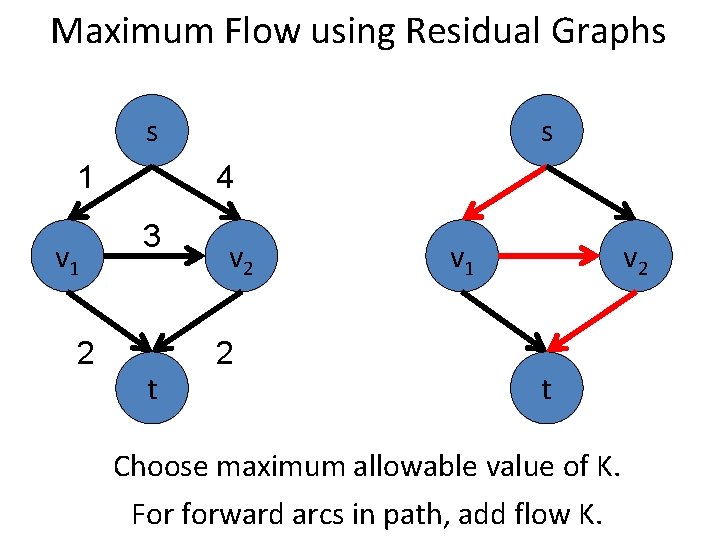
Maximum Flow using Residual Graphs s 2 v 1 1 s 4 3 t v 2 2 v 1 v 2 t Choose maximum allowable value of K. For forward arcs in path, add flow K.

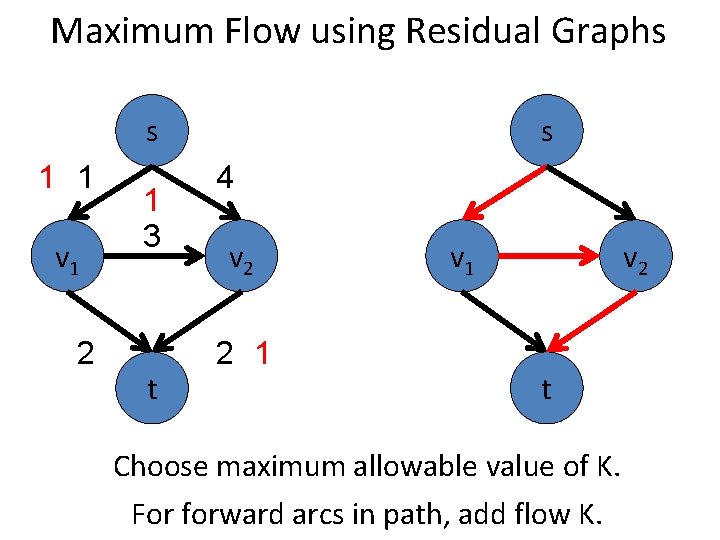
Maximum Flow using Residual Graphs s 2 2 v 1 1 2 3 t s 4 v 2 2 2 v 1 v 2 t Choose maximum allowable value of K. For forward arcs in path, add flow K.

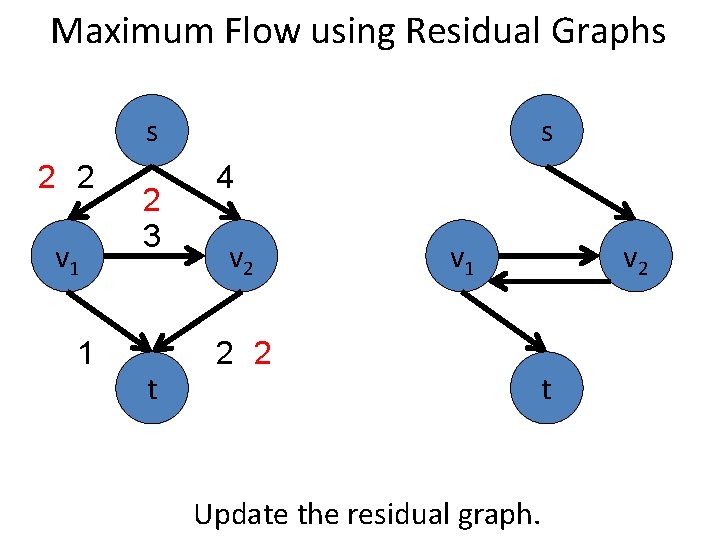
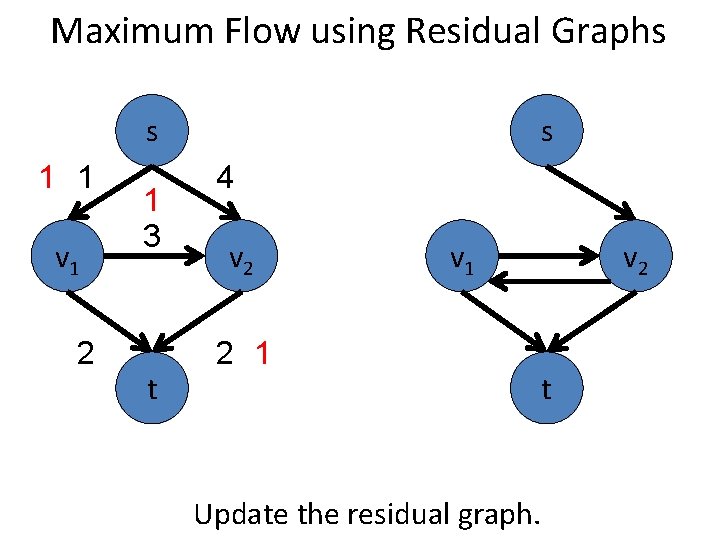
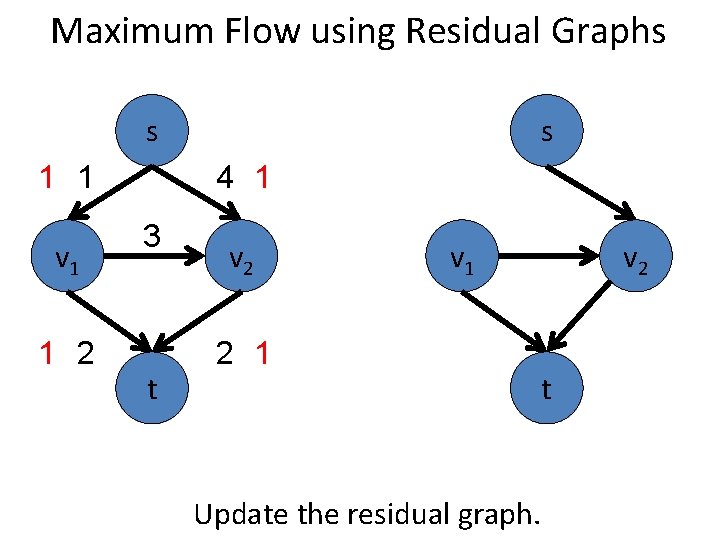
Maximum Flow using Residual Graphs s 2 2 v 1 1 2 3 t s 4 v 2 v 1 2 2 Update the residual graph. v 2 t

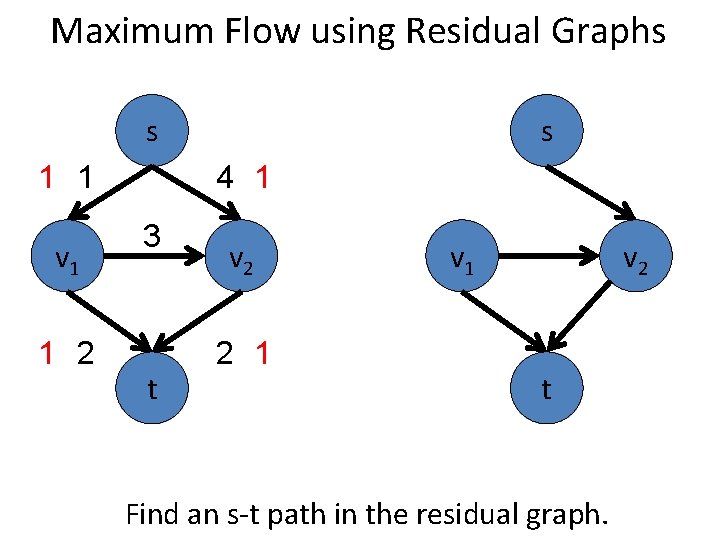
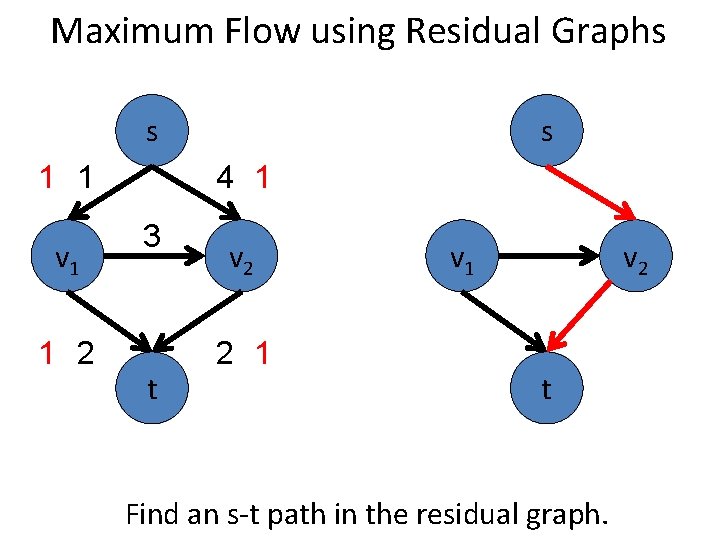
Maximum Flow using Residual Graphs s 2 2 v 1 1 2 3 t s 4 v 2 2 2 v 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 2 2 v 1 1 2 3 t s 4 v 2 2 2 v 1 v 2 t Find an s-t path in the residual graph.

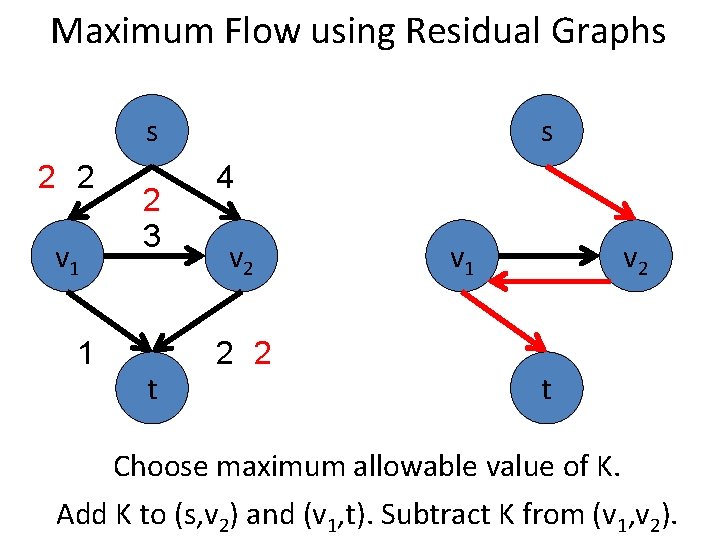
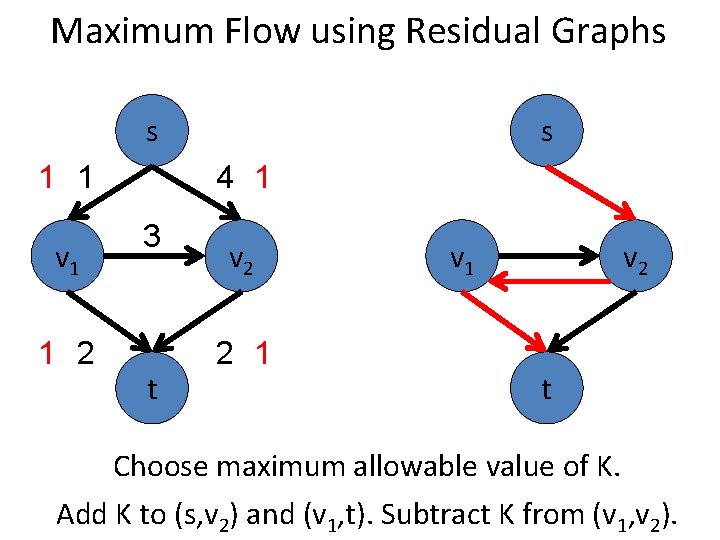
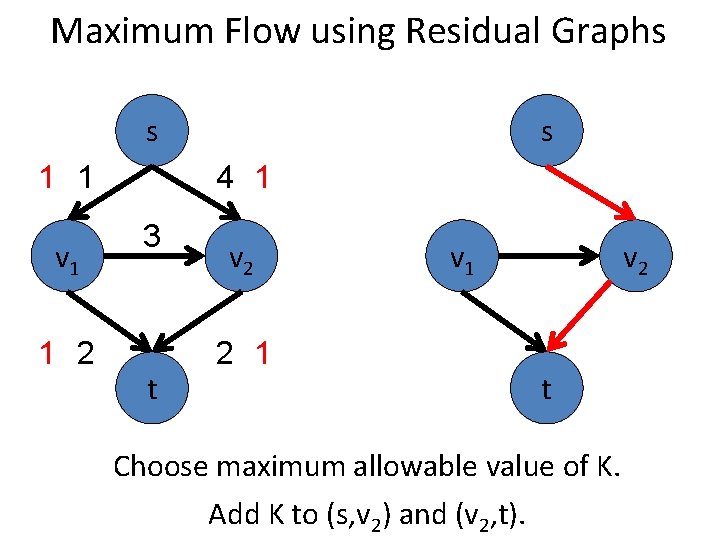
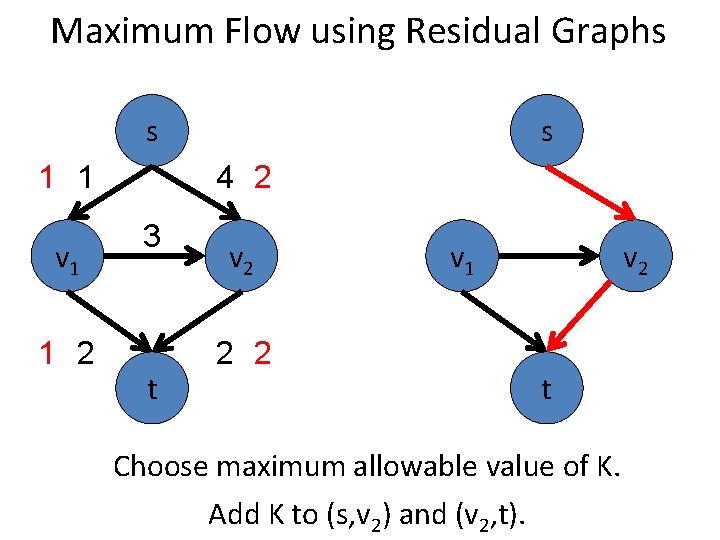
Maximum Flow using Residual Graphs s 2 2 v 1 1 2 3 t s 4 v 2 2 2 v 1 v 2 t Choose maximum allowable value of K. Add K to (s, v 2) and (v 1, t). Subtract K from (v 1, v 2).

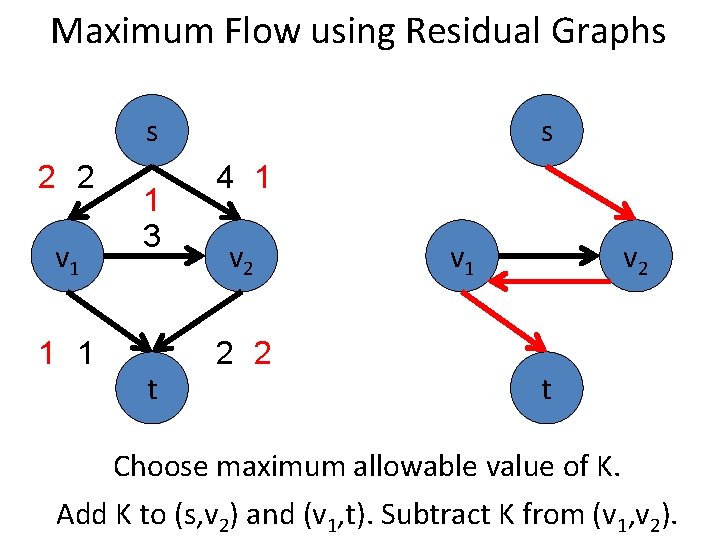
Maximum Flow using Residual Graphs s 2 2 v 1 1 3 t s 4 1 v 2 2 2 v 1 v 2 t Choose maximum allowable value of K. Add K to (s, v 2) and (v 1, t). Subtract K from (v 1, v 2).

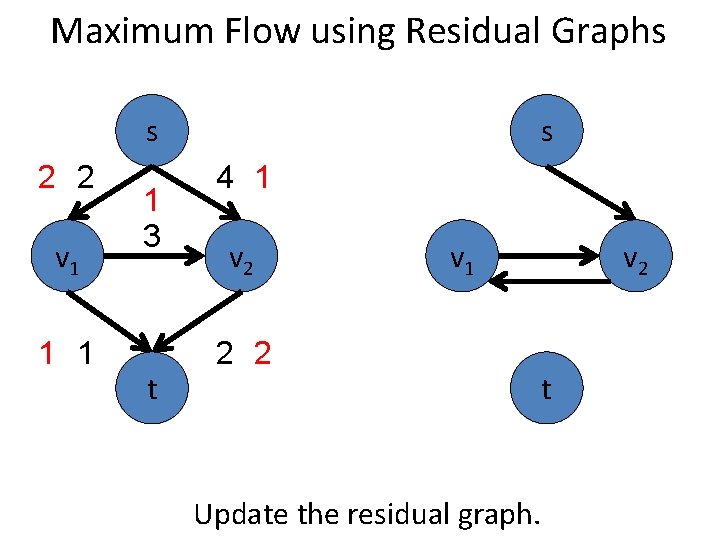
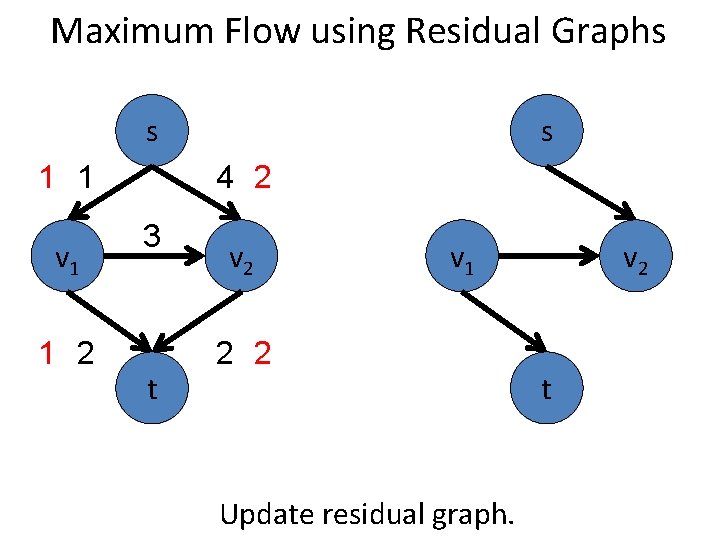
Maximum Flow using Residual Graphs s 2 2 v 1 1 3 t s 4 1 v 2 v 1 2 2 Update the residual graph. v 2 t

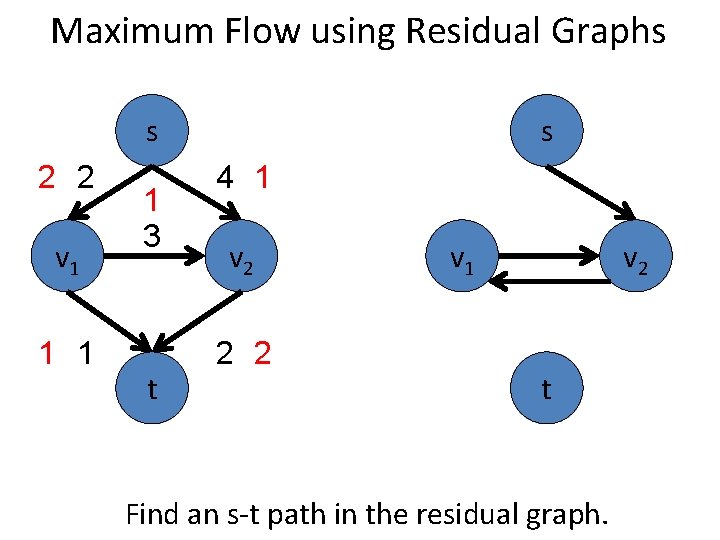
Maximum Flow using Residual Graphs s 2 2 v 1 1 3 t s 4 1 v 2 2 2 v 1 v 2 t Find an s-t path in the residual graph.

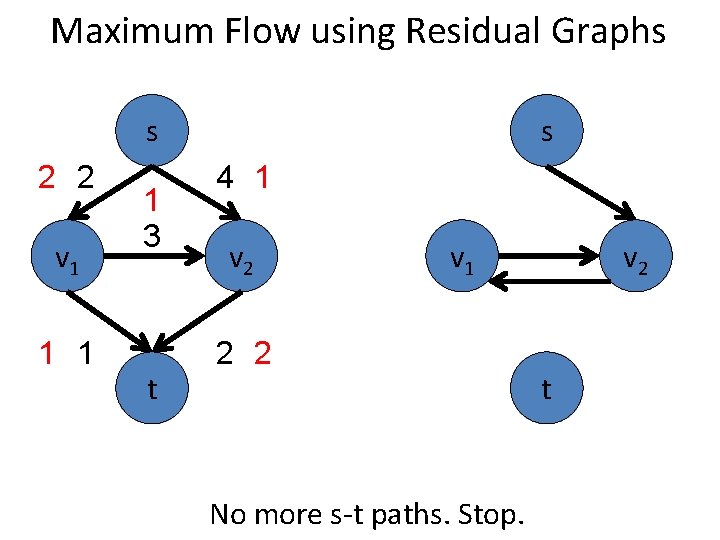
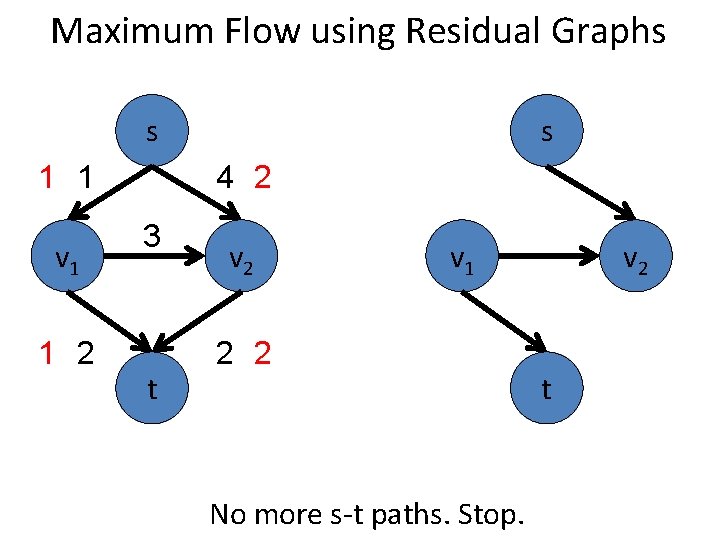
Maximum Flow using Residual Graphs s 2 2 v 1 1 3 t s 4 1 v 2 v 1 2 2 No more s-t paths. Stop. v 2 t

Maximum Flow using Residual Graphs s 2 2 v 1 1 3 t s 4 1 v 2 v 1 2 2 Correct Answer. v 2 t

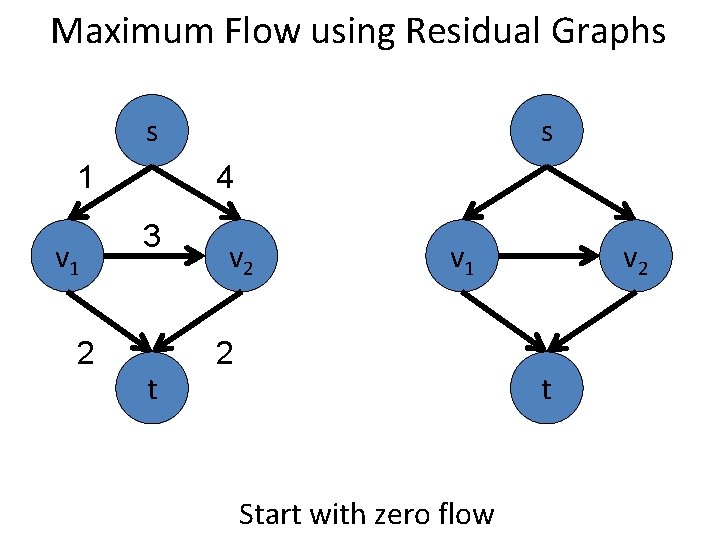
Maximum Flow using Residual Graphs s 1 v 1 2 s 4 3 t v 2 v 1 2 v 2 t Start with zero flow

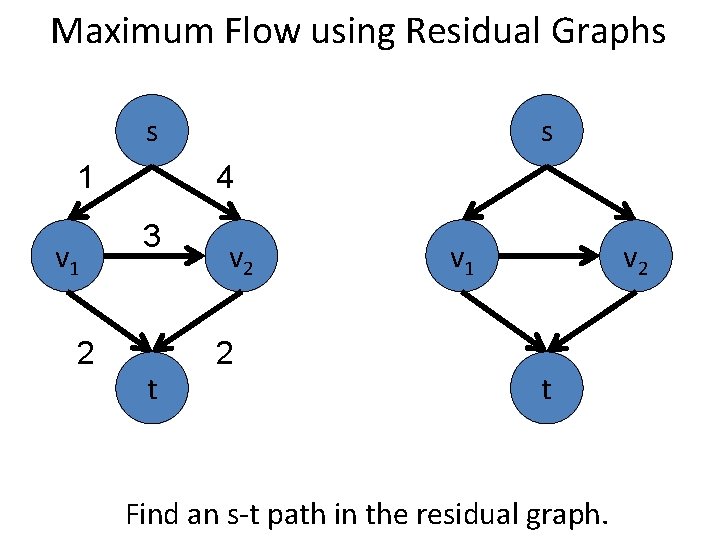
Maximum Flow using Residual Graphs s 1 v 1 2 s 4 3 t v 2 2 v 1 v 2 t Find an s-t path in the residual graph.

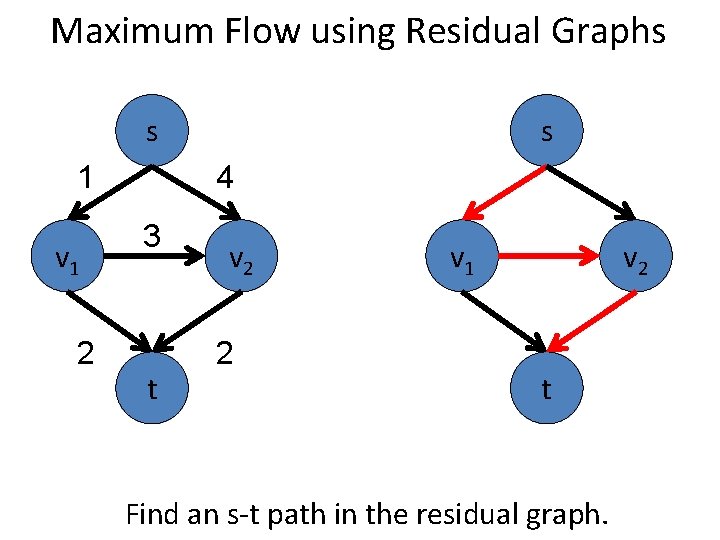
Maximum Flow using Residual Graphs s 1 v 1 2 s 4 3 t v 2 2 v 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 1 v 1 2 s 4 3 t v 2 2 v 1 v 2 t For inverse arcs in path, subtract flow K.

Maximum Flow using Residual Graphs s 1 v 1 2 s 4 3 t v 2 2 v 1 v 2 t Choose maximum allowable value of K. For forward arcs in path, add flow K.

Maximum Flow using Residual Graphs s 1 1 v 1 2 1 3 t s 4 v 2 2 1 v 2 t Choose maximum allowable value of K. For forward arcs in path, add flow K.

Maximum Flow using Residual Graphs s 1 1 v 1 2 1 3 t s 4 v 2 v 1 2 1 Update the residual graph. v 2 t

Maximum Flow using Residual Graphs s 1 1 v 1 2 1 3 t s 4 v 2 2 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 1 1 v 1 2 1 3 t s 4 v 2 2 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 1 1 v 1 2 1 3 t s 4 v 2 2 1 v 2 t Choose maximum allowable value of K. Add K to (s, v 2) and (v 1, t). Subtract K from (v 1, v 2).

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 1 3 t v 2 2 1 v 2 t Choose maximum allowable value of K. Add K to (s, v 2) and (v 1, t). Subtract K from (v 1, v 2).

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 1 3 t v 2 v 1 2 1 Update the residual graph. v 2 t

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 1 3 t v 2 2 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 1 3 t v 2 2 1 v 2 t Find an s-t path in the residual graph.

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 1 3 t v 2 2 1 v 2 t Choose maximum allowable value of K. Add K to (s, v 2) and (v 2, t).

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 2 3 t v 2 2 2 v 1 v 2 t Choose maximum allowable value of K. Add K to (s, v 2) and (v 2, t).

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 2 3 t v 2 v 1 2 2 Update residual graph. v 2 t

Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 2 3 t v 2 v 1 2 2 No more s-t paths. Stop. v 2 t

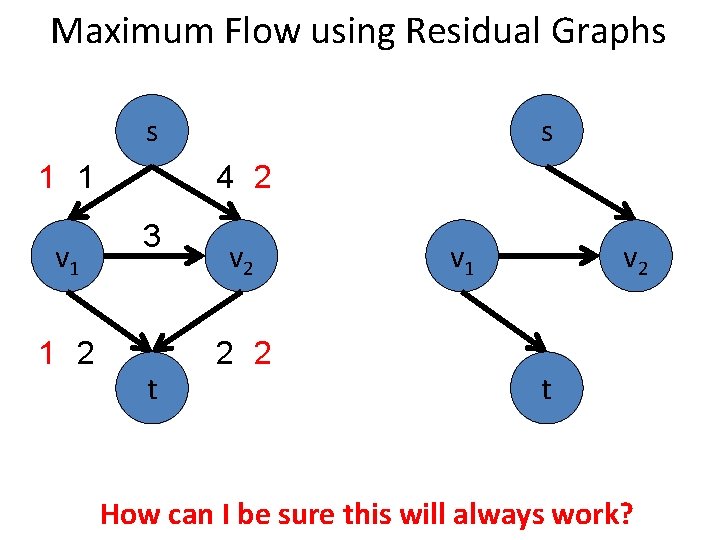
Maximum Flow using Residual Graphs s 1 1 v 1 1 2 s 4 2 3 t v 2 2 2 v 1 v 2 t How can I be sure this will always work?

Outline • Preliminaries • Maximum Flow – Residual Graph – Max-Flow Min-Cut Theorem • Algorithms

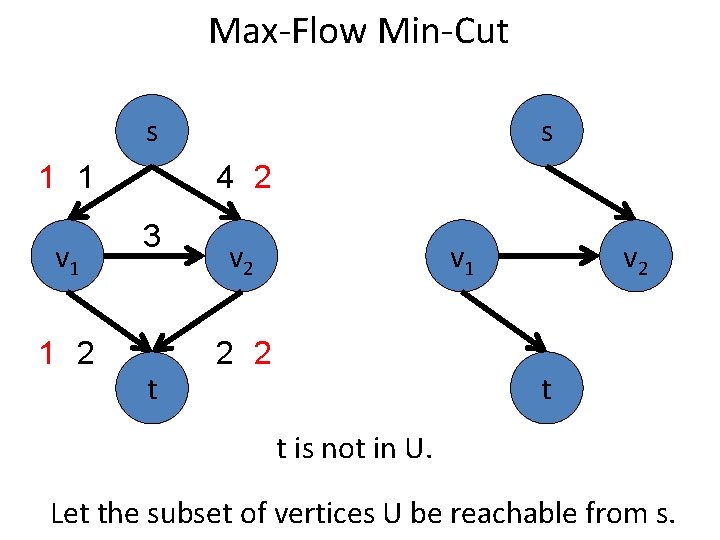
Max-Flow Min-Cut s 1 1 v 1 1 2 s 4 2 3 t v 2 v 1 2 2 v 2 t t is not in U. Let the subset of vertices U be reachable from s.

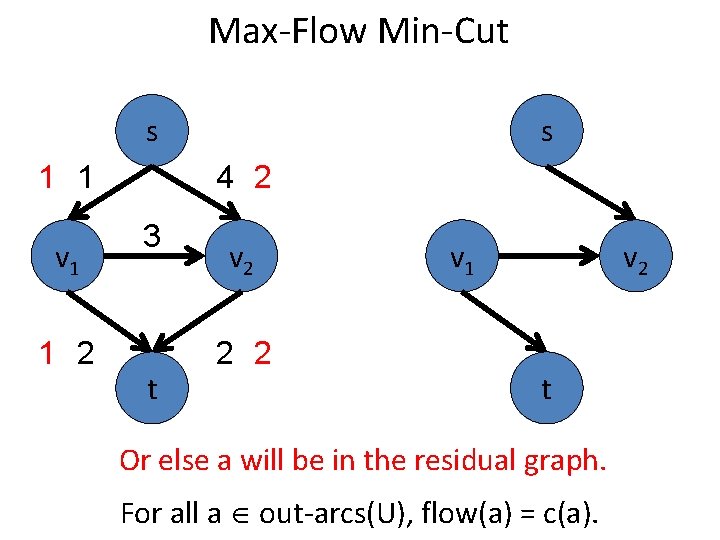
Max-Flow Min-Cut s 1 1 v 1 1 2 s 4 2 3 t v 2 2 2 v 1 v 2 t Or else a will be in the residual graph. For all a out-arcs(U), flow(a) = c(a).

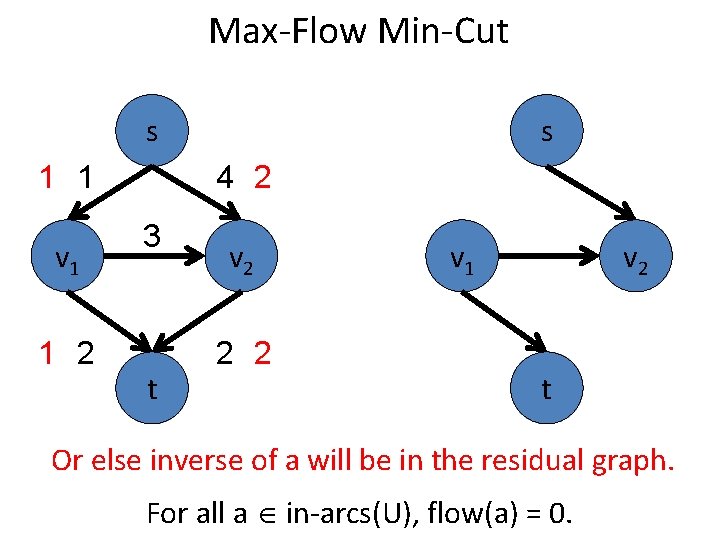
Max-Flow Min-Cut s 1 1 v 1 1 2 s 4 2 3 t v 2 2 2 v 1 v 2 t Or else inverse of a will be in the residual graph. For all a in-arcs(U), flow(a) = 0.

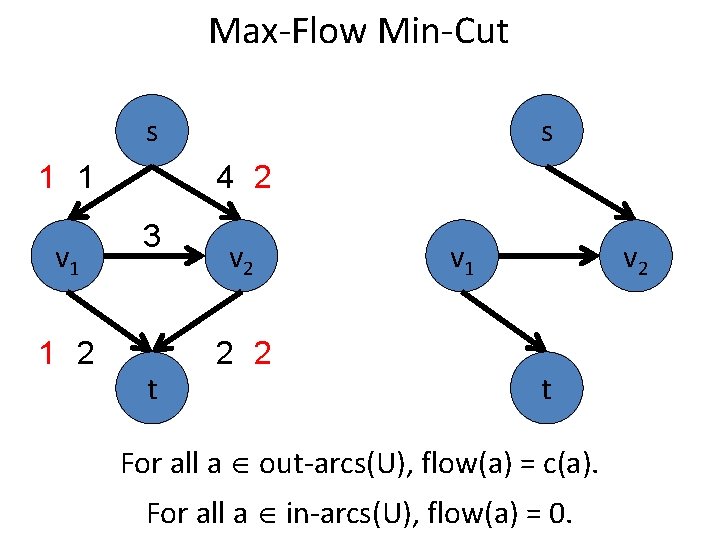
Max-Flow Min-Cut s 1 1 v 1 1 2 s 4 2 3 t v 2 2 2 v 1 v 2 t For all a out-arcs(U), flow(a) = c(a). For all a in-arcs(U), flow(a) = 0.

Flows vs. Cuts Value of flow = -Eflow(s) - Σv U{s} Eflow(v) = -Eflow(U) = flow(out-arcs(U)) - flow(in-arcs(U)) = Capacity of C flow(a) = c(a), a out-arcs(U) flow(a) = 0, a in-arcs(U)

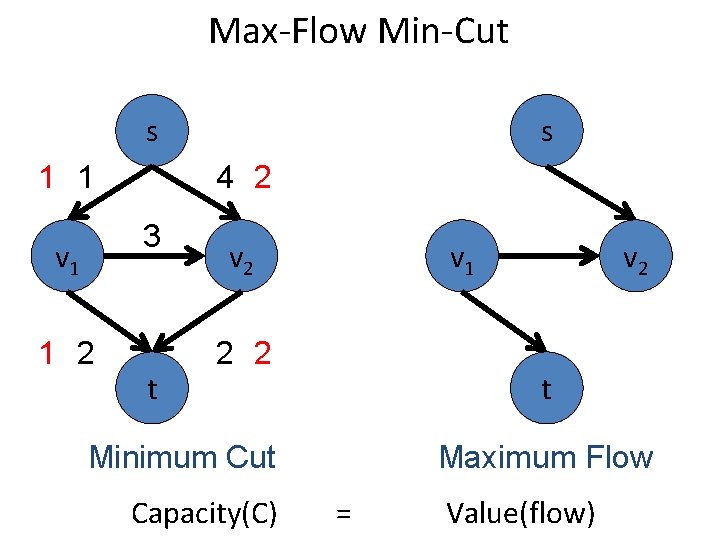
Max-Flow Min-Cut s 1 1 4 2 3 v 1 1 2 s t v 2 v 1 2 2 t Minimum Cut Capacity(C) v 2 Maximum Flow = Value(flow)

Outline • Preliminaries • Maximum Flow • Algorithms – Ford-Fulkerson Algorithm – Dinits Algorithm

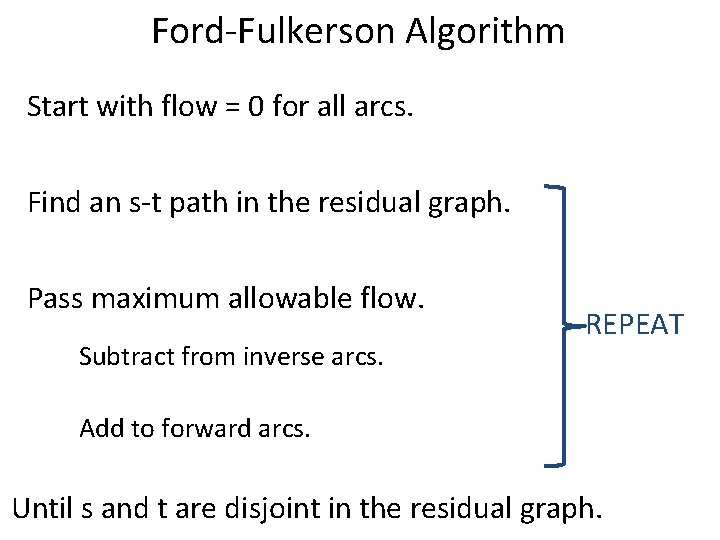
Ford-Fulkerson Algorithm Start with flow = 0 for all arcs. Find an s-t path in the residual graph. Pass maximum allowable flow. Subtract from inverse arcs. REPEAT Add to forward arcs. Until s and t are disjoint in the residual graph.

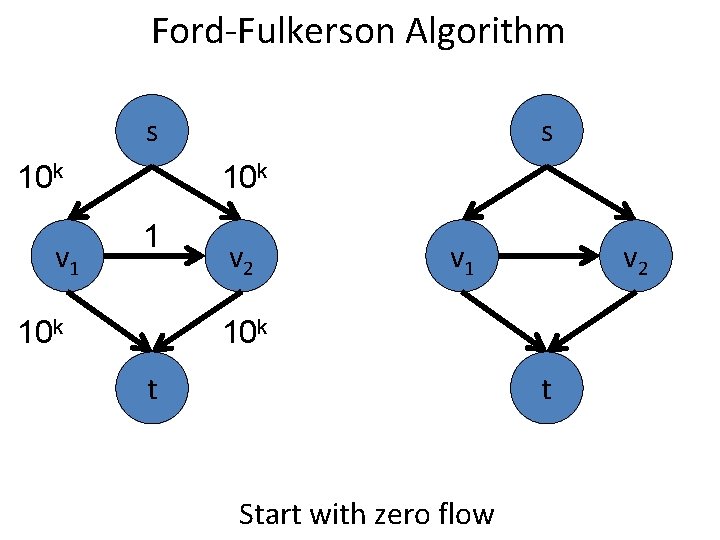
Ford-Fulkerson Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Start with zero flow

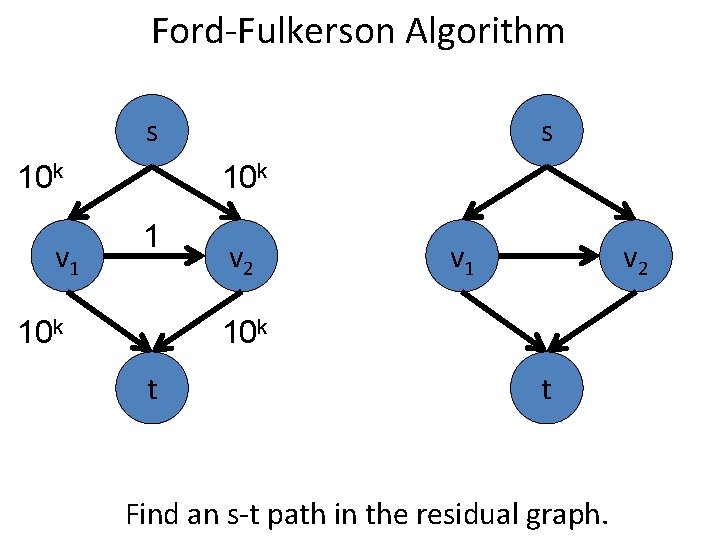
Ford-Fulkerson Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Find an s-t path in the residual graph.

Ford-Fulkerson Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Find an s-t path in the residual graph.

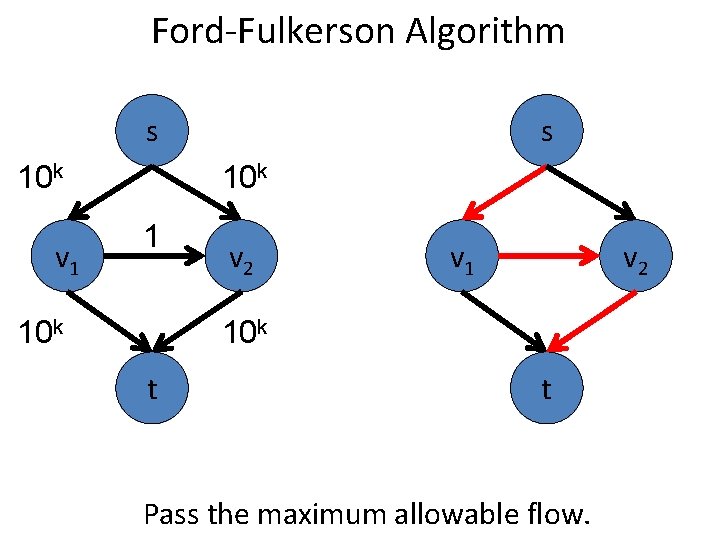
Ford-Fulkerson Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Pass the maximum allowable flow.

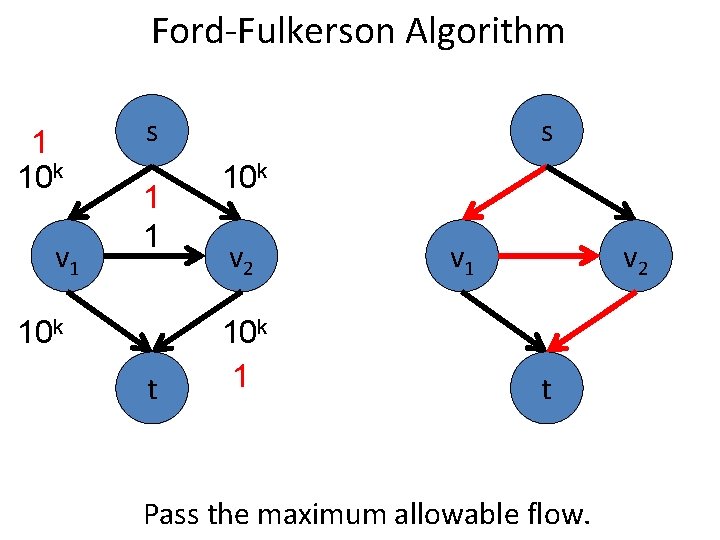
Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 10 k 1 v 2 t Pass the maximum allowable flow.

Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 v 1 10 k 1 Update the residual graph. v 2 t

Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 10 k 1 v 2 t Find an s-t path in the residual graph.

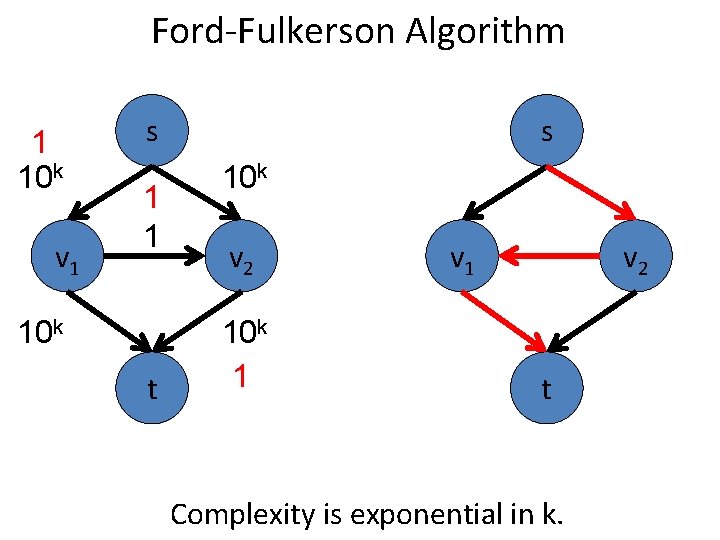
Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 10 k 1 v 2 t Find an s-t path in the residual graph.

Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 10 k 1 v 2 t Complexity is exponential in k.

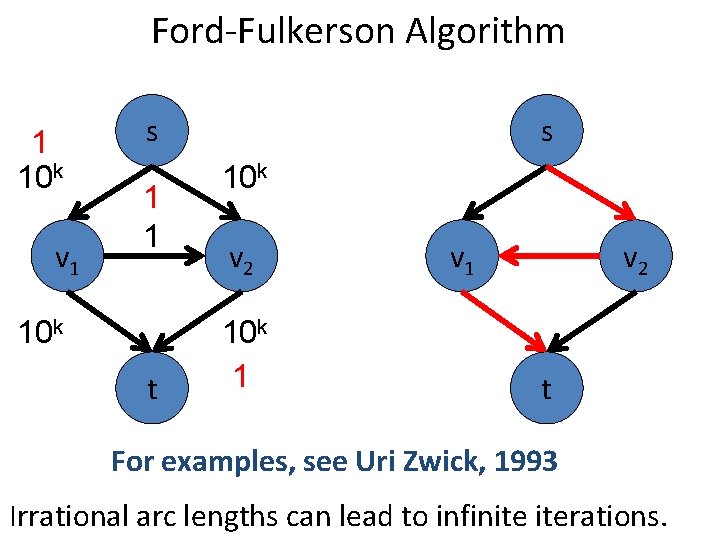
Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 10 k 1 v 2 t For examples, see Uri Zwick, 1993 Irrational arc lengths can lead to infinite iterations.

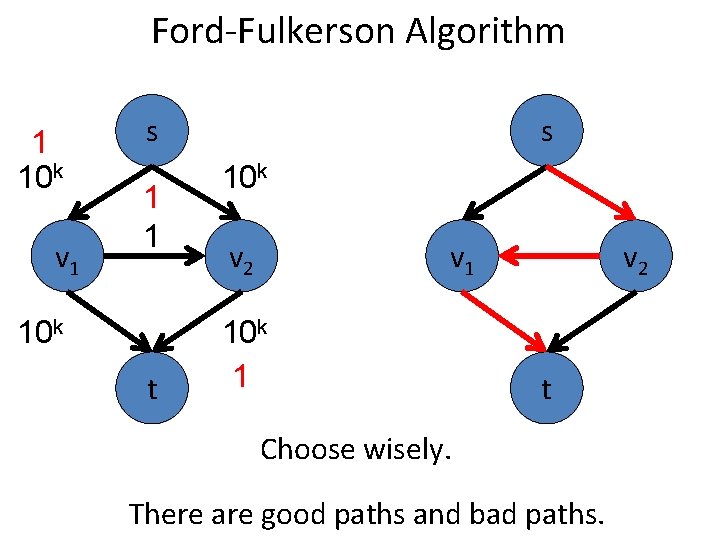
Ford-Fulkerson Algorithm 1 10 k v 1 s 1 1 10 k t s 10 k v 2 v 1 10 k 1 v 2 t Choose wisely. There are good paths and bad paths.

Outline • Preliminaries • Maximum Flow • Algorithms – Ford-Fulkerson Algorithm – Dinits Algorithm (Simple Version)

Dinits Algorithm Start with flow = 0 for all arcs. Find the minimum s-t path in the residual graph. Pass maximum allowable flow. Subtract from inverse arcs. REPEAT Add to forward arcs. Until s and t are disjoint in the residual graph.

Dinits Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Start with zero flow

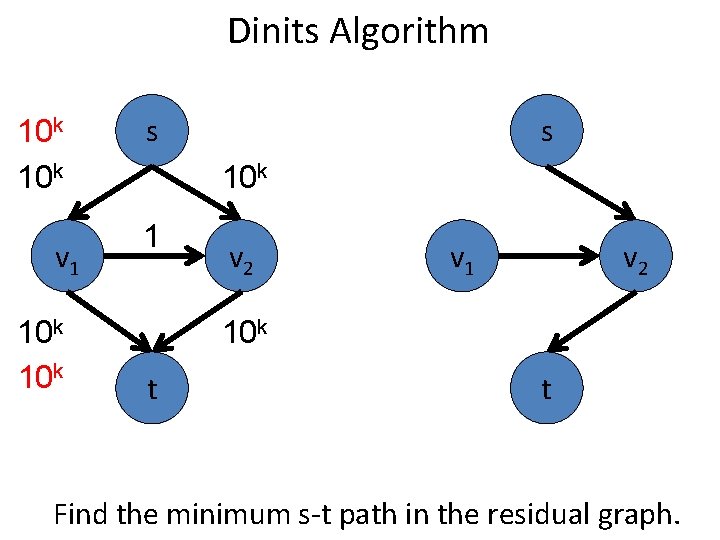
Dinits Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Find the minimum s-t path in the residual graph.

Dinits Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Find the minimum s-t path in the residual graph.

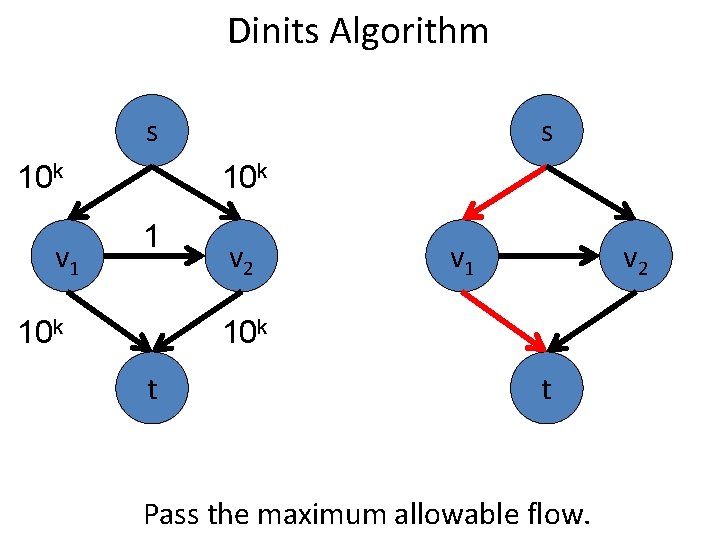
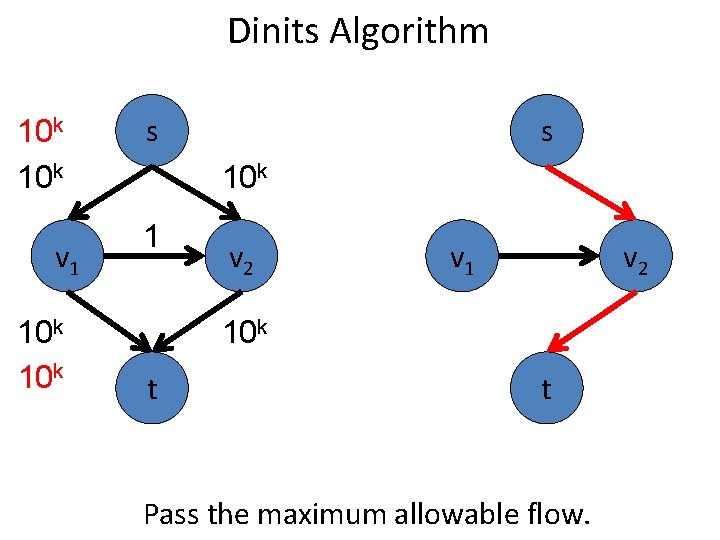
Dinits Algorithm s 10 k v 1 s 10 k 1 10 k v 2 v 1 v 2 10 k t t Pass the maximum allowable flow.

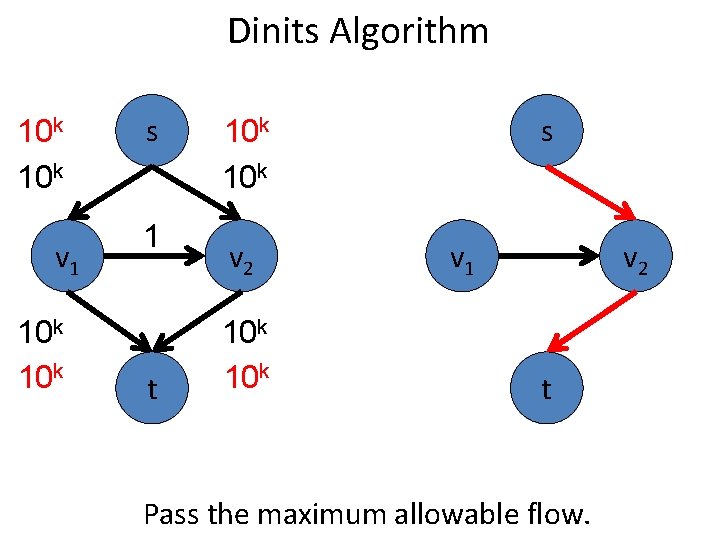
Dinits Algorithm 10 k v 1 10 k s s 10 k 1 v 2 v 1 v 2 10 k t t Pass the maximum allowable flow.

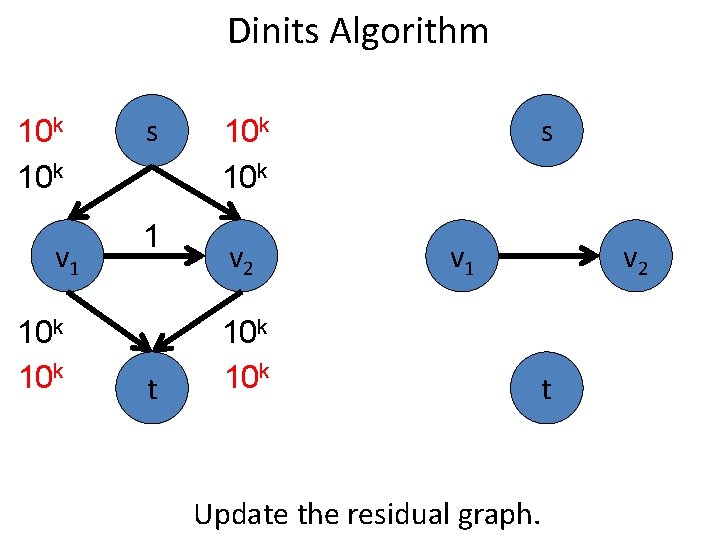
Dinits Algorithm 10 k v 1 10 k s s 10 k 1 v 2 v 1 v 2 10 k t t Update the residual graph.

Dinits Algorithm 10 k v 1 10 k s s 10 k 1 v 2 v 1 v 2 10 k t t Find the minimum s-t path in the residual graph.

Dinits Algorithm 10 k v 1 10 k s s 10 k 1 v 2 v 1 v 2 10 k t t Find the minimum s-t path in the residual graph.

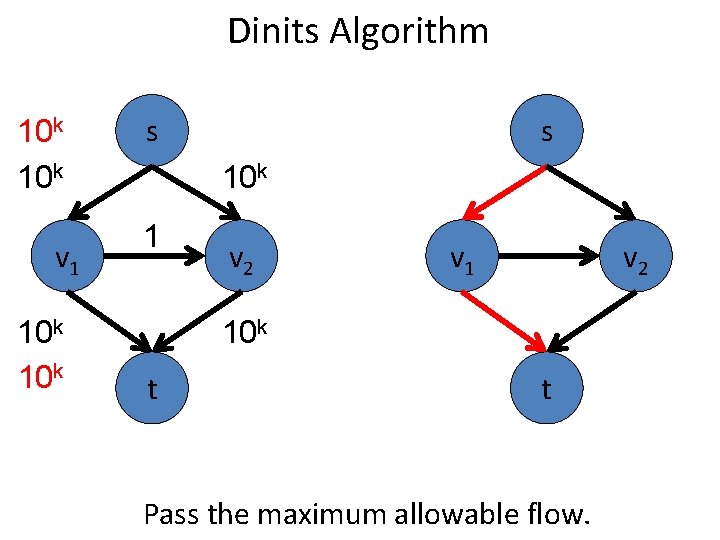
Dinits Algorithm 10 k v 1 10 k s s 10 k 1 v 2 v 1 v 2 10 k t t Pass the maximum allowable flow.

Dinits Algorithm 10 k v 1 10 k s 1 t s 10 k v 2 10 k v 1 v 2 t Pass the maximum allowable flow.

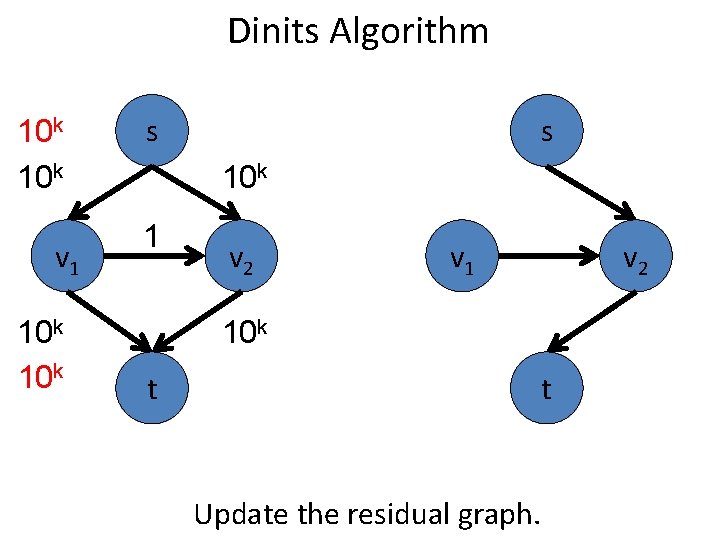
Dinits Algorithm 10 k v 1 10 k s 1 t s 10 k v 2 v 1 10 k Update the residual graph. v 2 t

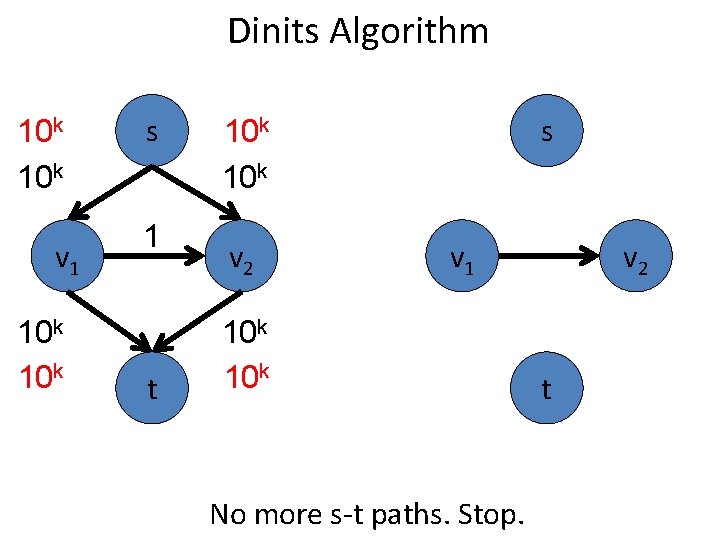
Dinits Algorithm 10 k v 1 10 k s 1 t s 10 k v 2 v 1 10 k No more s-t paths. Stop. v 2 t

Computational Complexity Strongly polynomial: O(m 2 n) m = |A|, n = |V| Finding shortest s-t path O(m) Number of iterations O(mn) Proof? First, a Lemma.

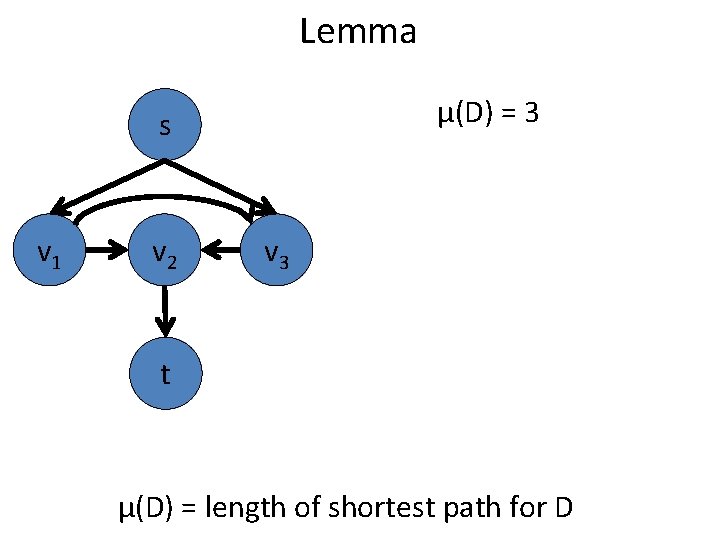
Lemma μ(D) = 3 s v 1 v 2 v 3 t μ(D) = length of shortest path for D

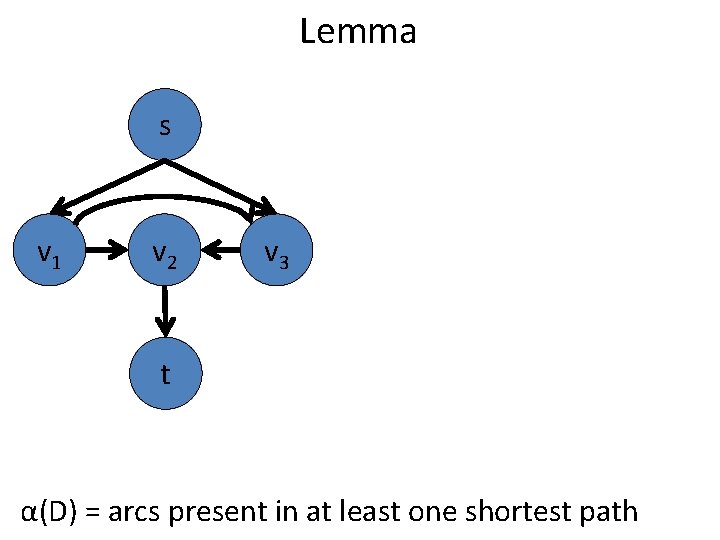
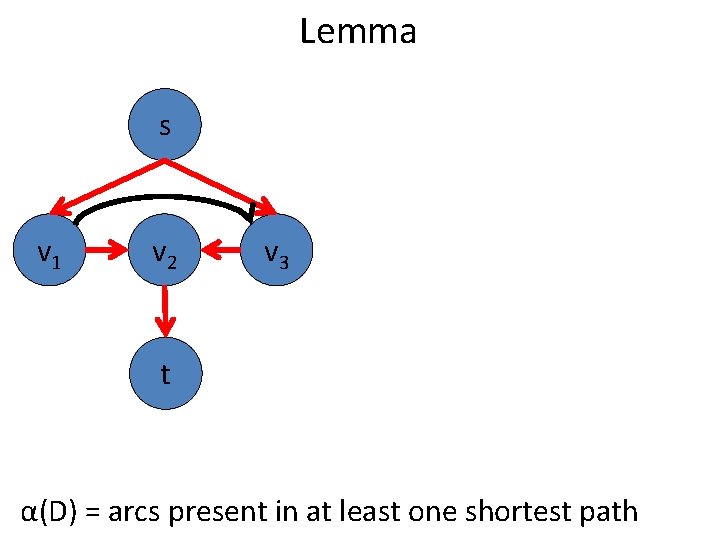
Lemma s v 1 v 2 v 3 t α(D) = arcs present in at least one shortest path

Lemma s v 1 v 2 v 3 t α(D) = arcs present in at least one shortest path

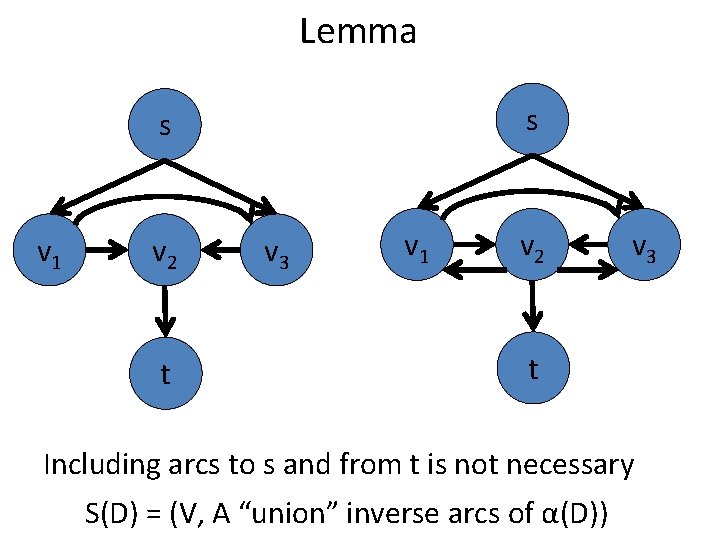
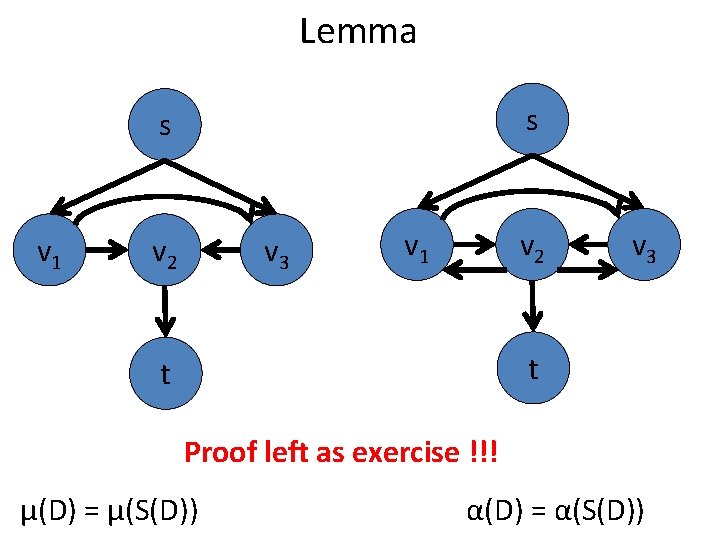
Lemma s s v 1 v 2 t v 3 v 1 v 2 v 3 t Including arcs to s and from t is not necessary S(D) = (V, A “union” inverse arcs of α(D))

Lemma s s v 1 v 2 v 3 t t Proof left as exercise !!! μ(D) = μ(S(D)) α(D) = α(S(D))

Computational Complexity Strongly polynomial: O(m 2 n) m = |A|, n = |V| Finding shortest s-t path O(m) Number of iterations O(mn)

Computational Complexity Current residual graph D 0 Find a shortest path P in D 0 New residual graph D 1 is a subgraph of S(D 0) μ(D 1) ≥ μ(S(D 0)) = μ(D 0)

Computational Complexity At least one arc a in P, a α(D 0) and a α(D 1) Specifically, an arc that is saturated in path P μ(D 1) ≥ μ(S(D 0)) = μ(D 0) α(D 1) “subset of” Assume Equality α(S(D 0)) = α(D 0)

Computational Complexity At least one arc a in P, a α(D 0) and a α(D 1) Specifically, an arc that is saturated in path P μ(D 1) ≥ μ(S(D 0)) = μ(D 0) α(D 1) Assume Equality “strict subset of” α(S(D 0)) = α(D 0)

Computational Complexity At each iteration, either μ increases Or size of α decreases Therefore, total iterations = O(mn) Overall complexity = O(m 2 n)

Let us take an example Image segmentation Image Segmentation Following slides based on P. Kohli’s tutorial

Let us take an example Image segmentation S T Image Construct a graph

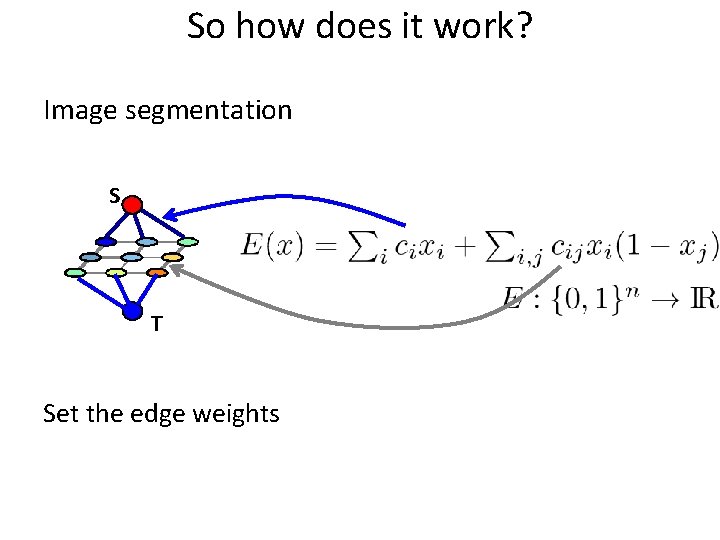
So how does it work? Image segmentation S T Set the edge weights

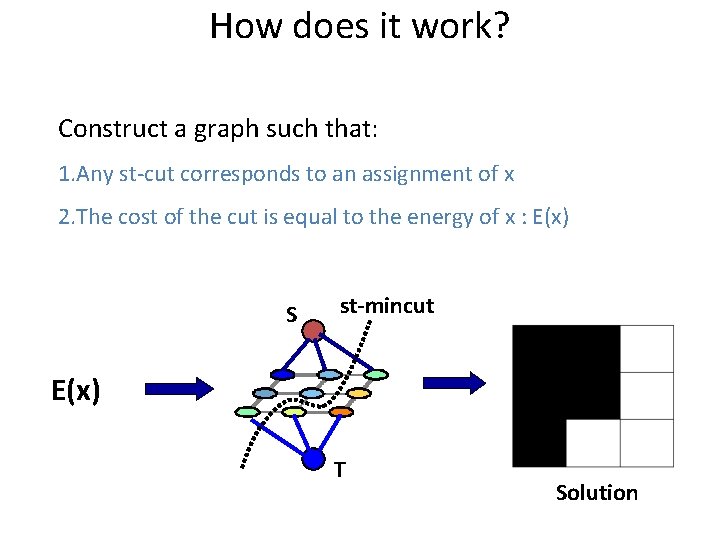
How does it work? Construct a graph such that: 1. Any st-cut corresponds to an assignment of x 2. The cost of the cut is equal to the energy of x : E(x) S st-mincut E(x) T Solution

Graph construction E(a 1, a 2) Source (0) a 1 a 2 Sink (1)

Graph construction E(a 1, a 2) = 2 a 1 Source (0) 2 a 1 a 2 Sink (1)

Graph construction E(a 1, a 2) = 2 a 1 + 5ā1 Source (0) 2 a 1 a 2 5 Sink (1)

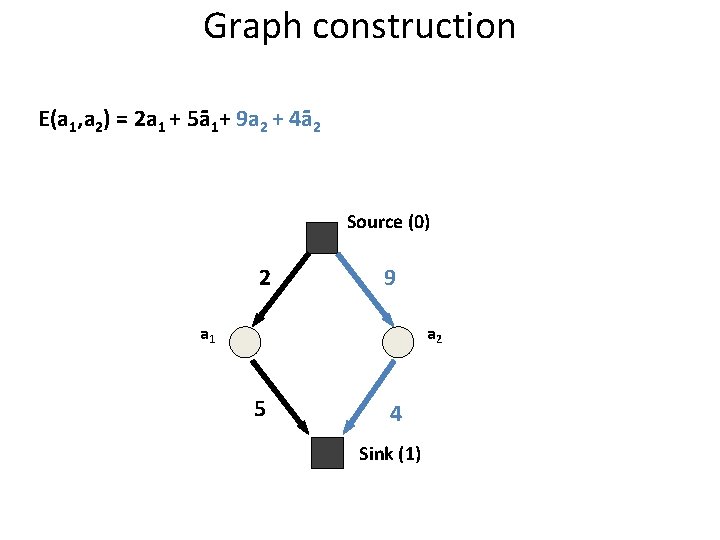
Graph construction E(a 1, a 2) = 2 a 1 + 5ā1+ 9 a 2 + 4ā2 Source (0) 2 9 a 1 a 2 5 4 Sink (1)

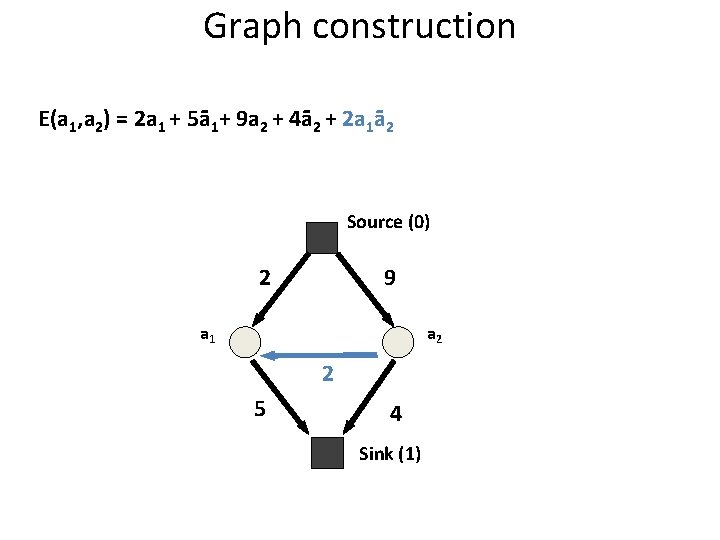
Graph construction E(a 1, a 2) = 2 a 1 + 5ā1+ 9 a 2 + 4ā2 + 2 a 1ā2 Source (0) 9 2 a 1 a 2 2 5 4 Sink (1)

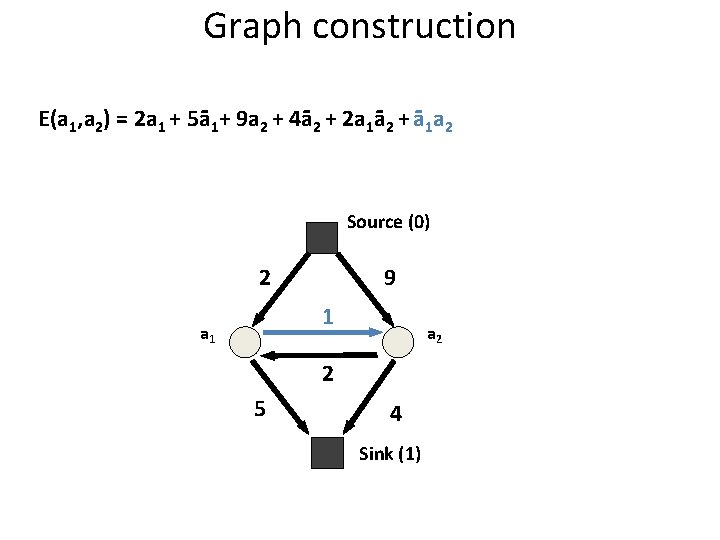
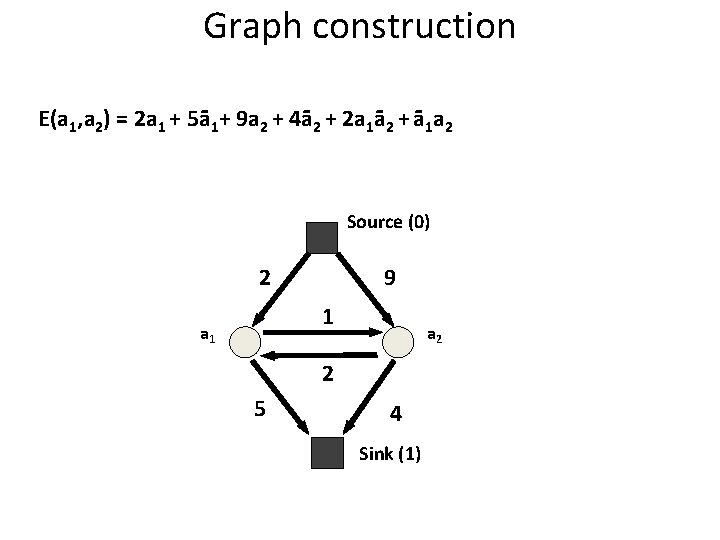
Graph construction E(a 1, a 2) = 2 a 1 + 5ā1+ 9 a 2 + 4ā2 + 2 a 1ā2 + ā1 a 2 Source (0) 9 2 1 a 2 2 5 4 Sink (1)

Graph construction E(a 1, a 2) = 2 a 1 + 5ā1+ 9 a 2 + 4ā2 + 2 a 1ā2 + ā1 a 2 Source (0) 9 2 1 a 2 2 5 4 Sink (1)

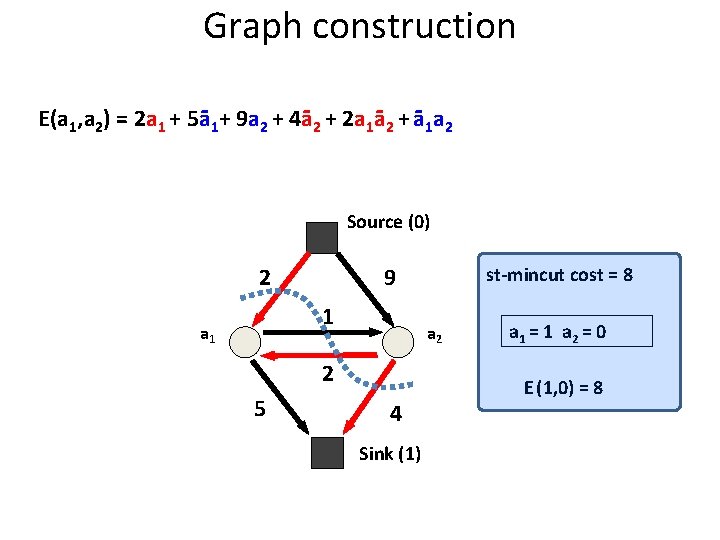
Graph construction E(a 1, a 2) = 2 a 1 + 5ā1+ 9 a 2 + 4ā2 + 2 a 1ā2 + ā1 a 2 Source (0) 9 2 1 a 2 2 5 st-mincut cost = 8 4 Sink (1) a 1 = 1 a 2 = 0 E (1, 0) = 8