Discrete Optimization in Computer Vision Nikos Komodakis Ecole

Discrete Optimization in Computer Vision Nikos Komodakis Ecole des Ponts Paris. Tech, LIGM Traitement de l’information et vision artificielle

Message passing algorithms for energy minimization

Message-passing algorithms n n n Central concept: messages These methods work by propagating messages across the MRF graph Widely used algorithms in many areas

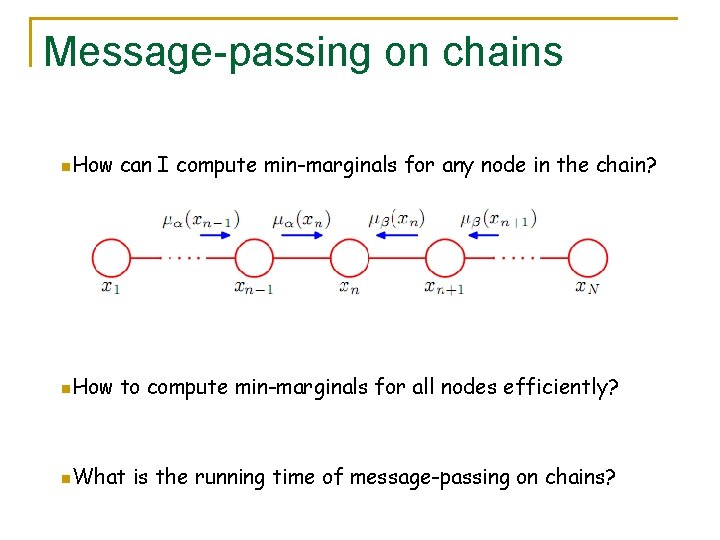
Message-passing algorithms n n But how do messages relate to optimizing the energy? Let’s look at a simple example first: we will examine the case where the MRF graph is a chain

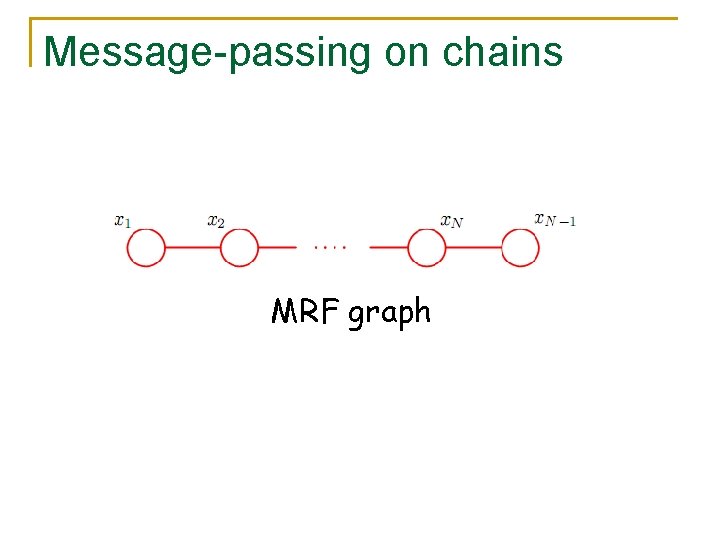
Message-passing on chains MRF graph

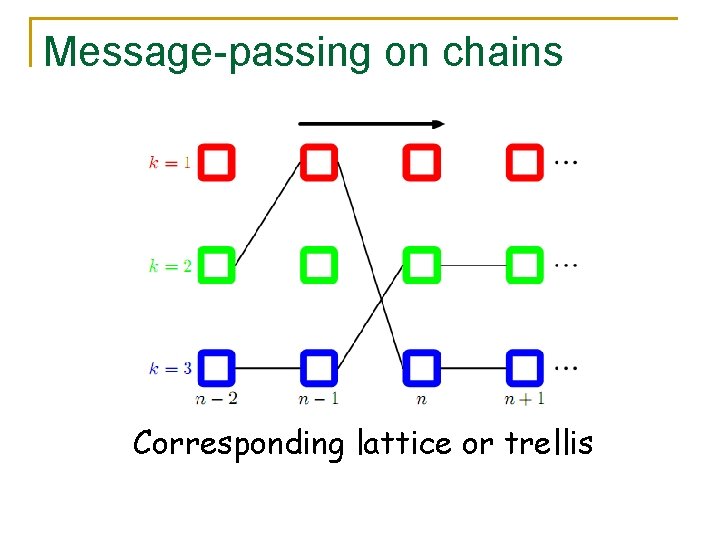
Message-passing on chains Corresponding lattice or trellis

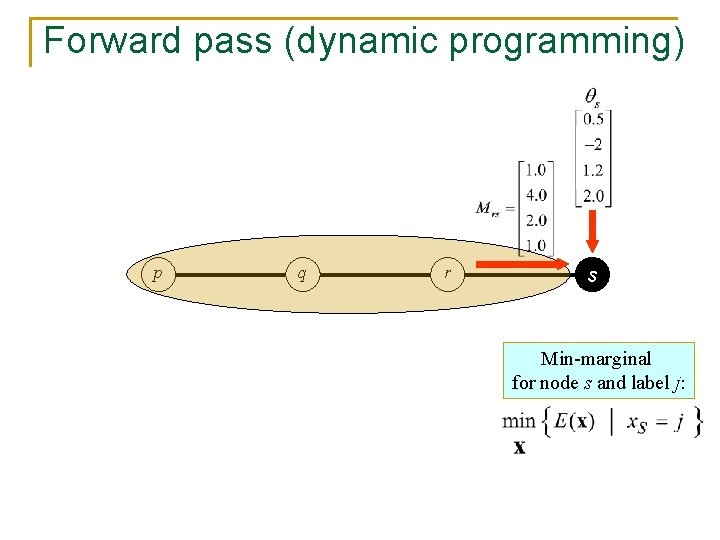
Message-passing on chains n n Global minimum in linear time Optimization proceeds in two passes: n Forward pass (dynamic programming) n Backward pass

Message-passing on chains (example on board) (algebraic derivation of messages)

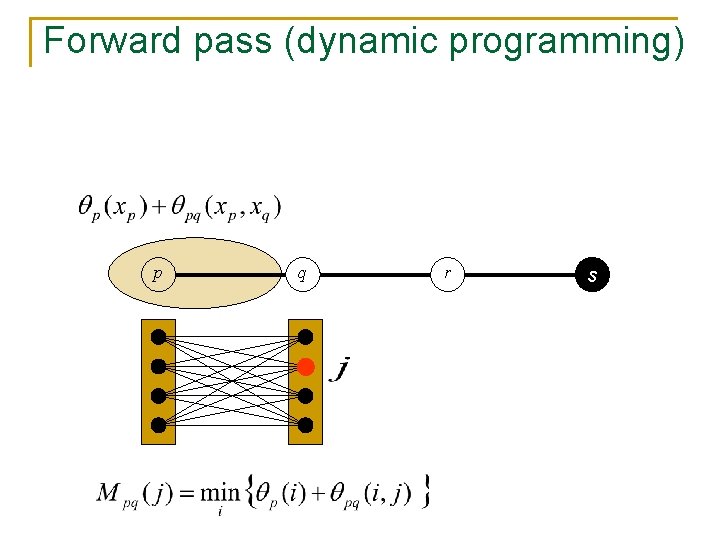
Message-passing on chains p q r s

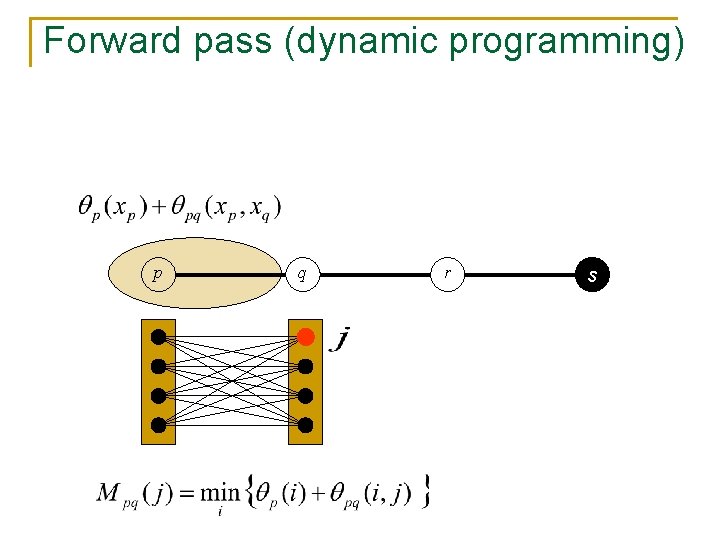
Forward pass (dynamic programming) p q r s

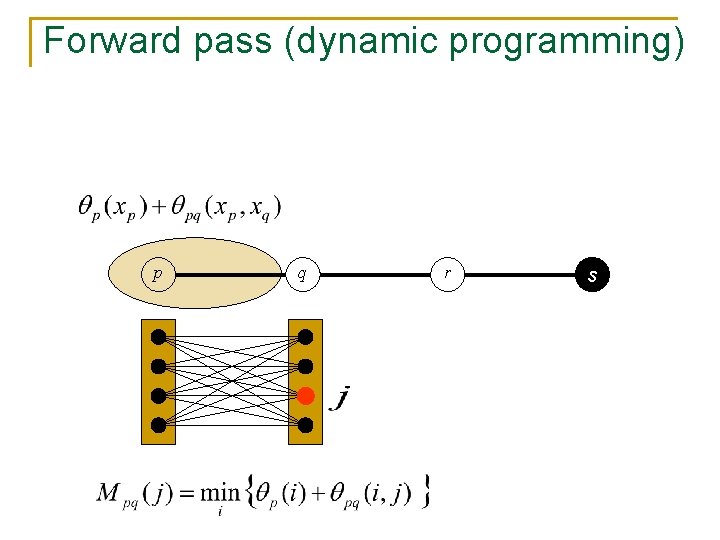
Forward pass (dynamic programming) p q r s

Forward pass (dynamic programming) p q r s

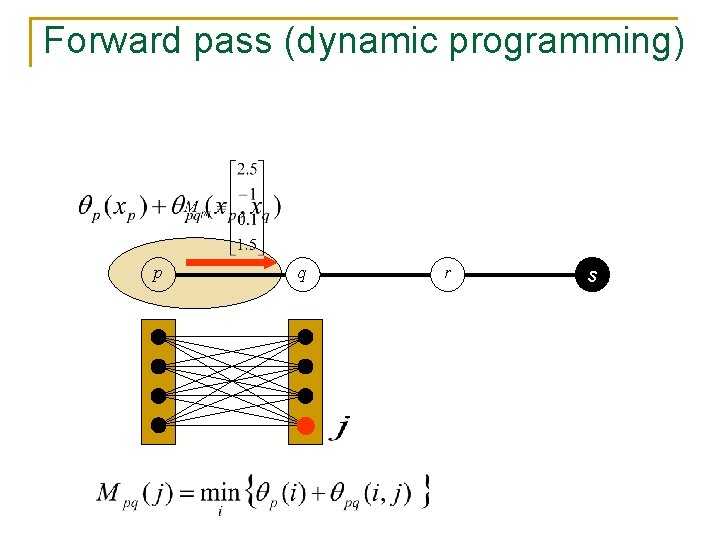
Forward pass (dynamic programming) p q r s

Forward pass (dynamic programming) p q r s

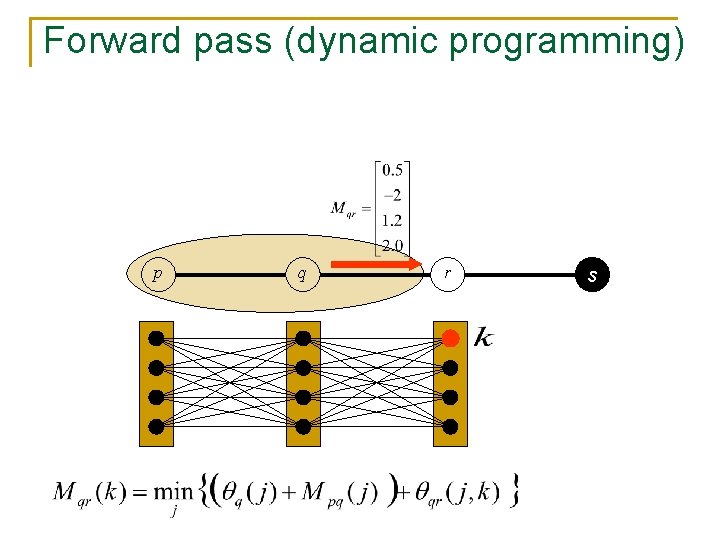
Forward pass (dynamic programming) p q r s Min-marginal for node s and label j:

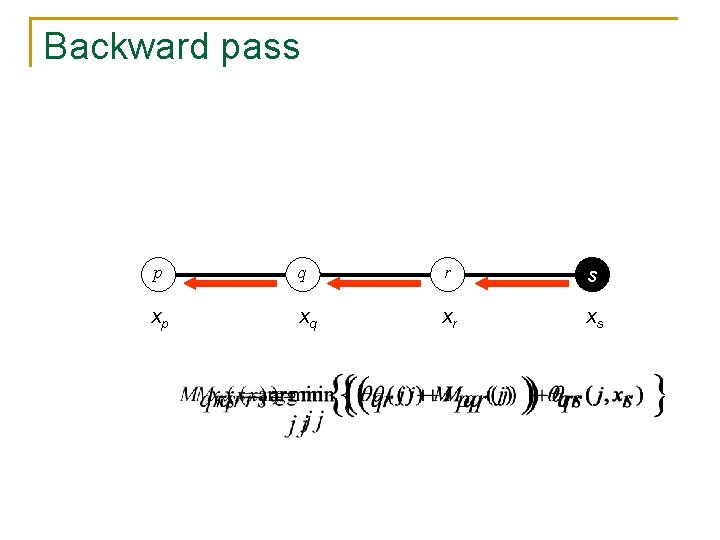
Backward pass p q r s xp xq xr xs

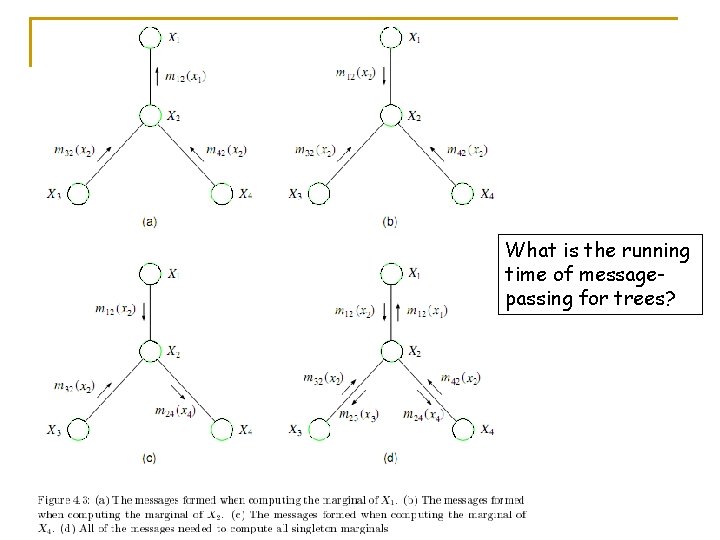
Message-passing on chains n. How can I compute min-marginals for any node in the chain? n. How to compute min-marginals for all nodes efficiently? n. What is the running time of message-passing on chains?

Message-passing on trees n n n We can apply the same idea to treestructured graphs Slight generalization from chains Resulting algorithm called: belief propagation (also called under many other names: e. g. , max-product, min-sum etc. ) (for chains, it is also often called the Viterbi algorithm)

Belief propagation (BP)

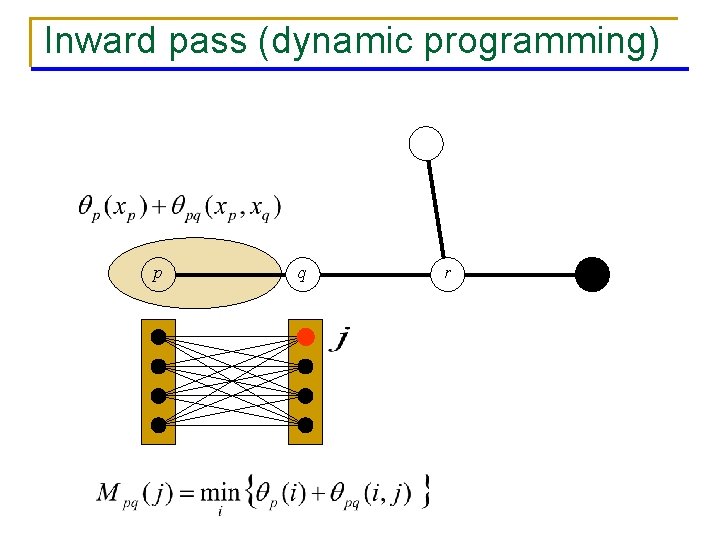
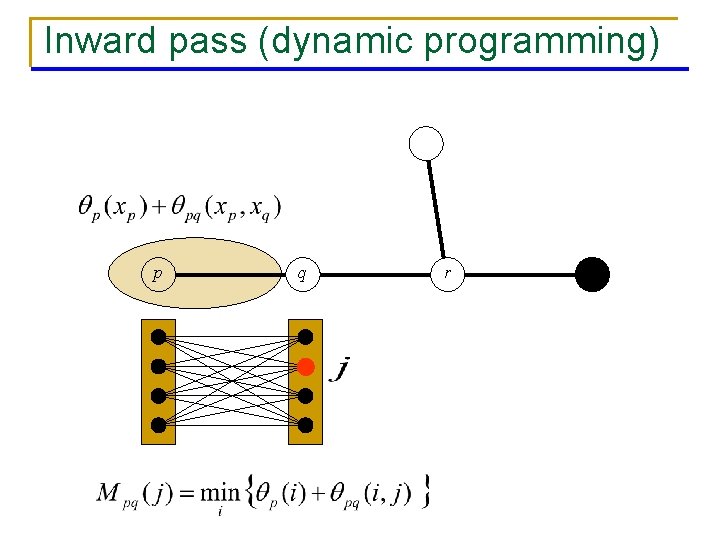
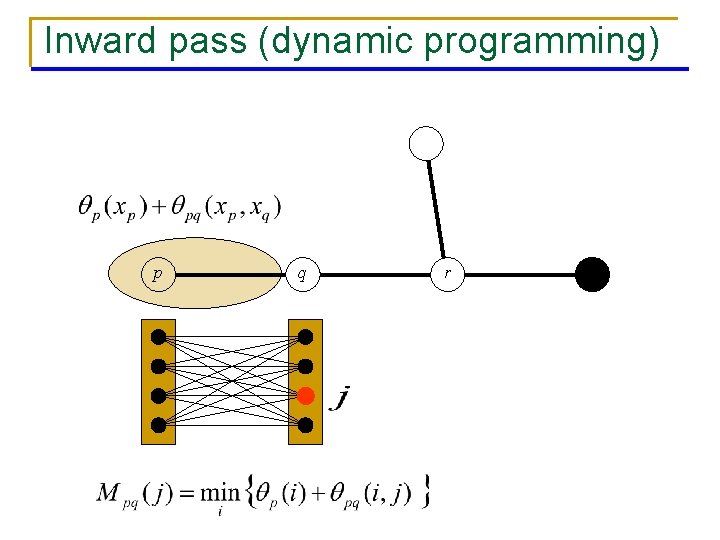
BP on a tree [Pearl’ 88] leaf p q leaf n n r root Dynamic programming: global minimum in linear time BP: q Inward pass (dynamic programming) q Outward pass q Gives min-marginals

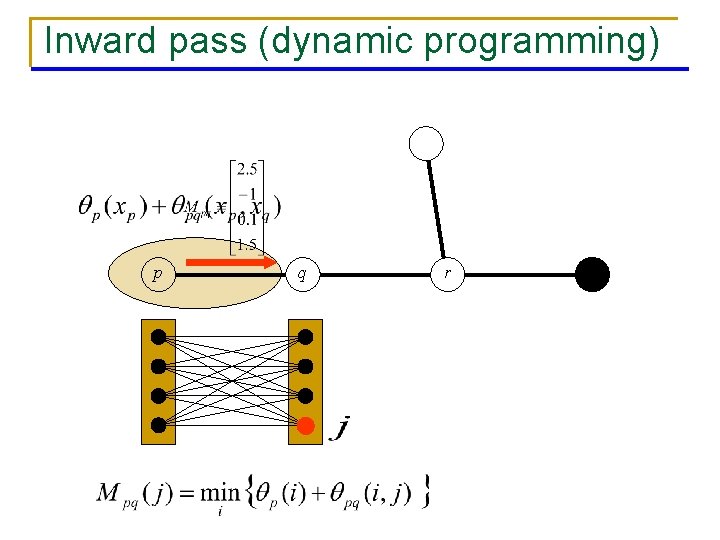
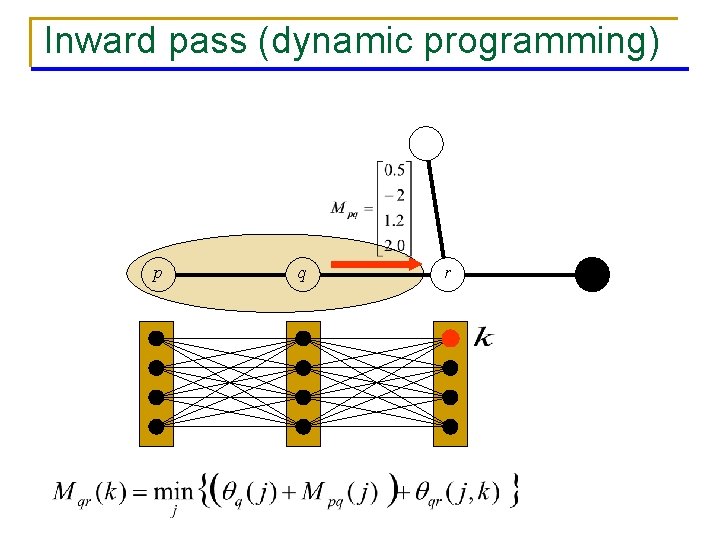
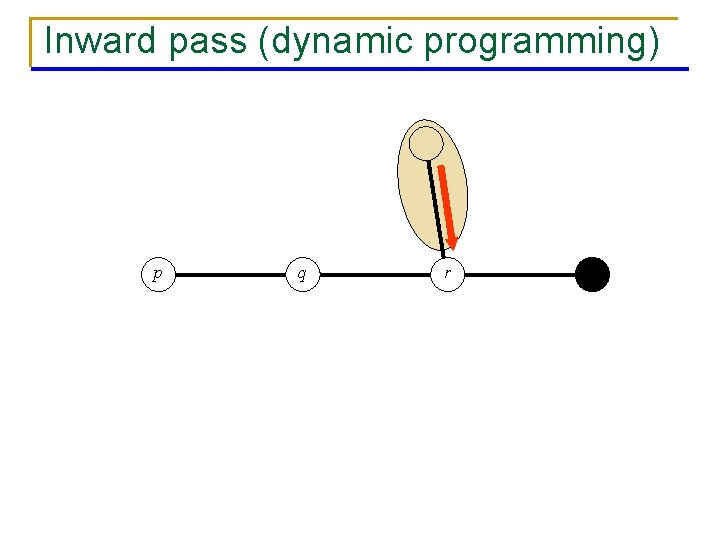
Inward pass (dynamic programming) p q r

Inward pass (dynamic programming) p q r

Inward pass (dynamic programming) p q r

Inward pass (dynamic programming) p q r

Inward pass (dynamic programming) p q r

Inward pass (dynamic programming) p q r

Inward pass (dynamic programming) p q r

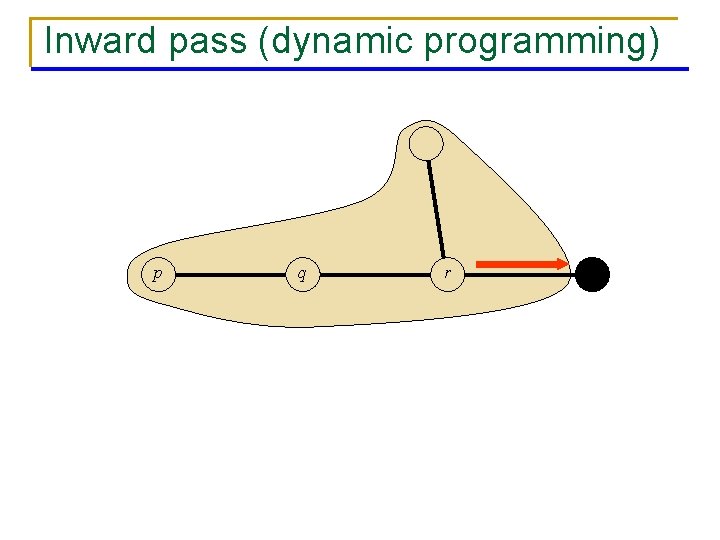
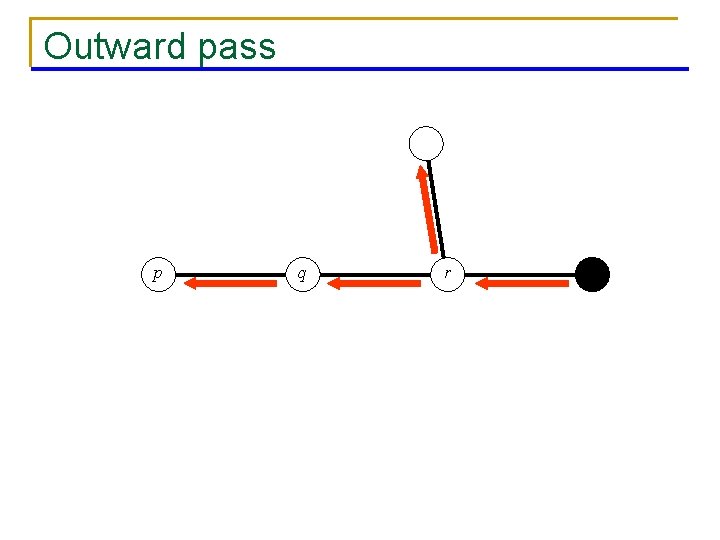
Outward pass p q r

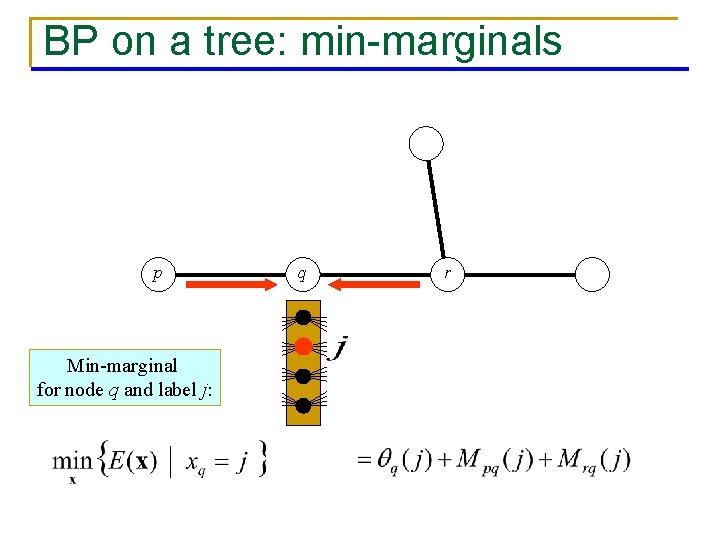
BP on a tree: min-marginals p Min-marginal for node q and label j: q r

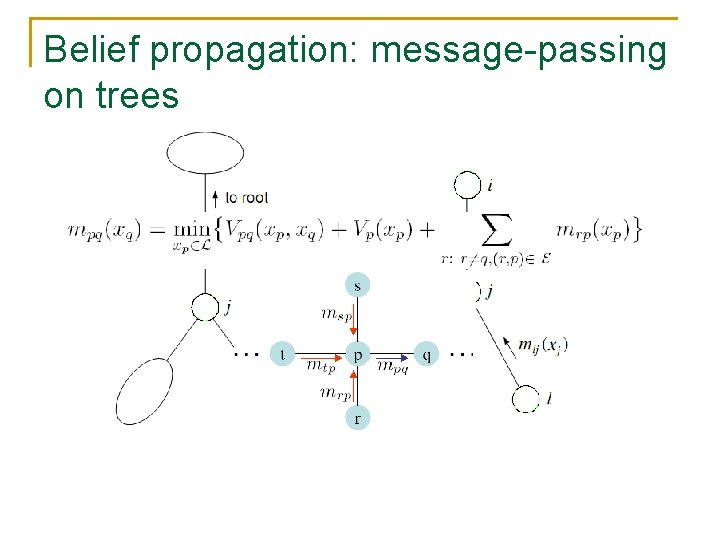
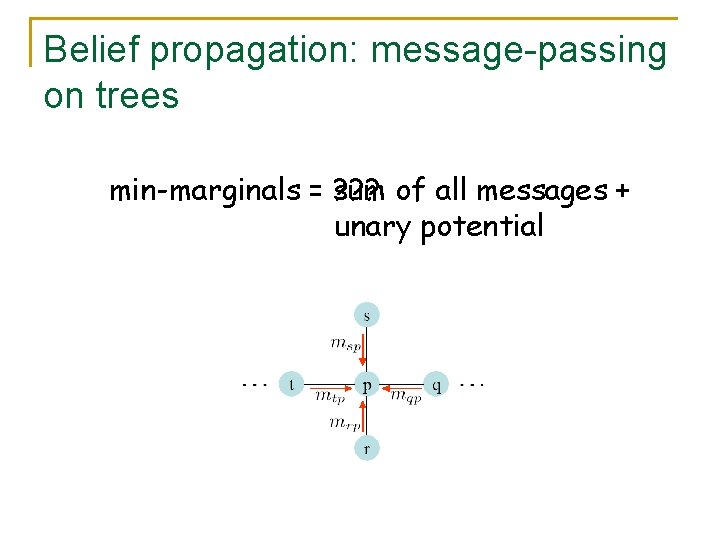
Belief propagation: message-passing on trees

Belief propagation: message-passing on trees min-marginals = ? ? ? sum of all messages + unary potential

What is the running time of messagepassing for trees?

Message-passing on chains n n Essentially, message passing on chains is dynamic programming Dynamic programming means reuse of computations

Generalizing belief propagation n Key property: min(a+b, a+c) = a+min(b, c) BP can be generalized to any operators satisfying the above property E. g. , instead of (min, +), we could have: q q (max, *) Resulting algorithm called max-product. What does it compute? (+, *) Resulting algorithm called sum-product. What does it compute?

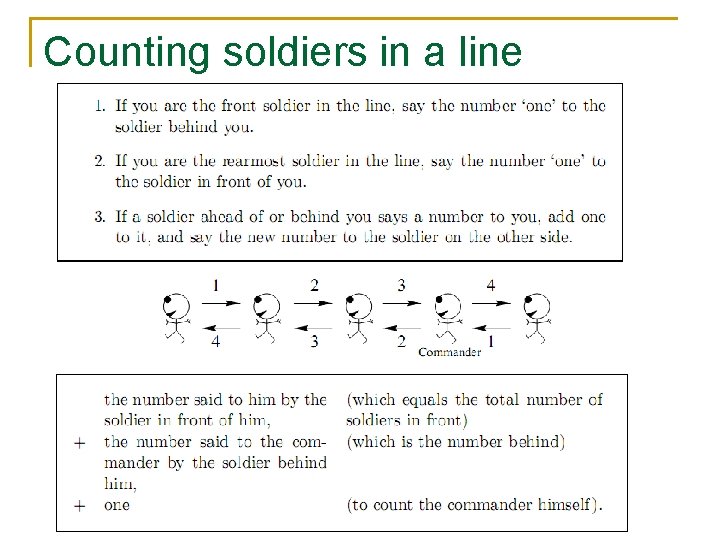
Belief propagation as a distributive algorithm n BP works distributively (as a result, it can be parallelized) n Essentially BP is a decentralized algorithm n Global results through local exchange of information n Simple example to illustrate this: counting soldiers

Counting soldiers in a line (From David Mac. Kay’s book “Information Theory, Inference, and Learning”) n Can you think of a distributive algorithm for the commander to count its soldiers?

Counting soldiers in a line

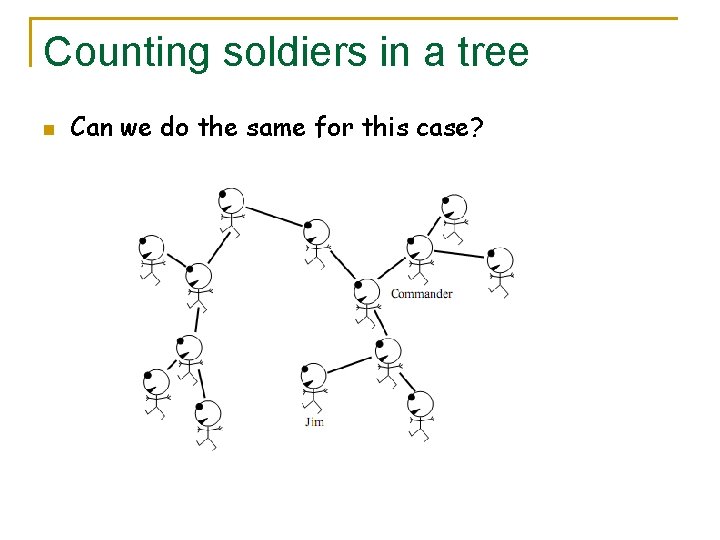
Counting soldiers in a tree n Can we do the same for this case?

Counting soldiers in a tree

Counting soldiers n n Simple example to illustrate BP Same idea can be used in cases which are seemingly more complex: q q n counting paths through a point in a grid probability of passing through a node in the grid In general, we have used the same idea for minimizing MRFs (a much more general problem)

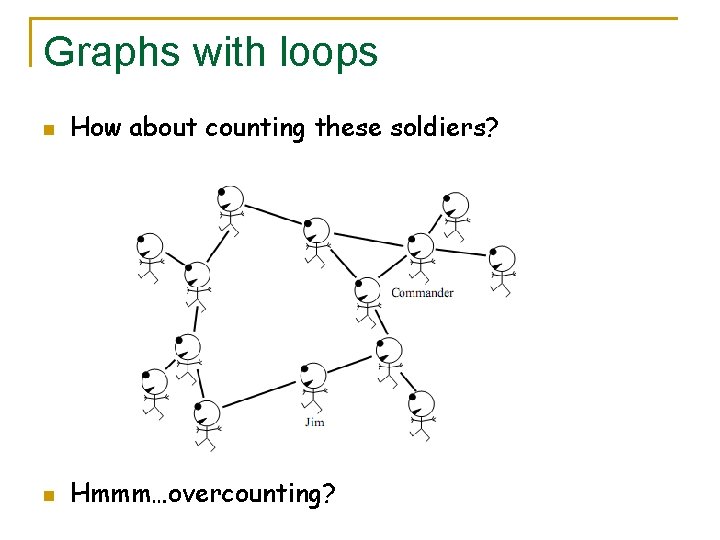
Graphs with loops n How about counting these soldiers? n Hmmm…overcounting?