Discrete Mathematics Unit 1 Set Theory and Logic











































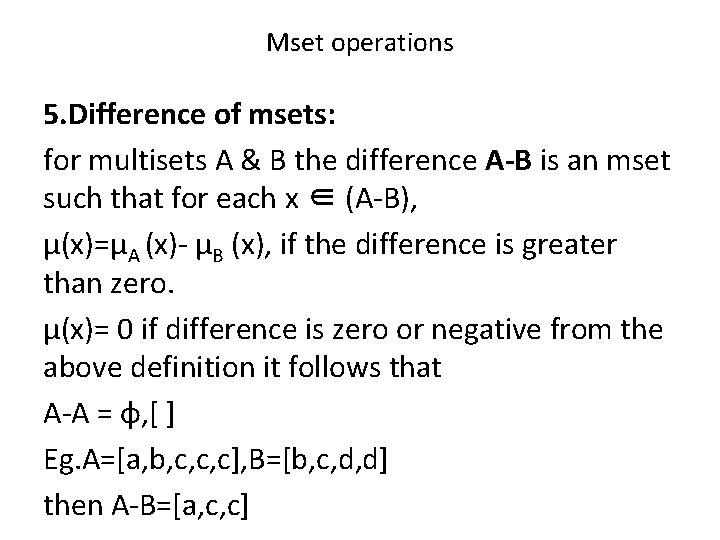
















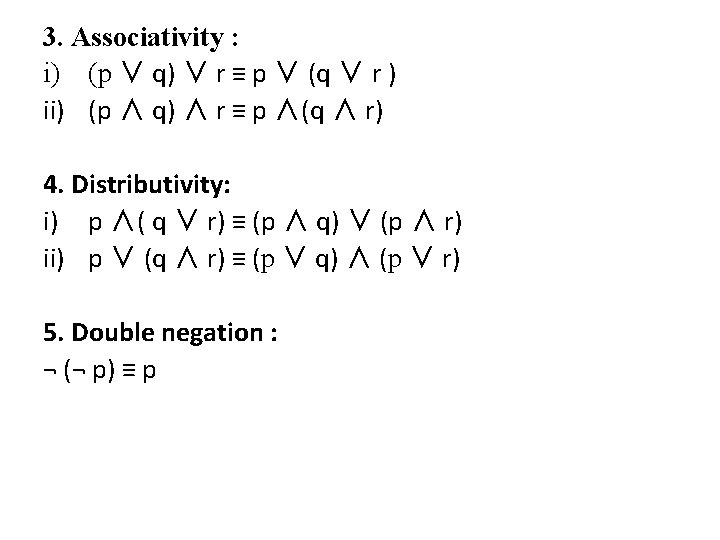












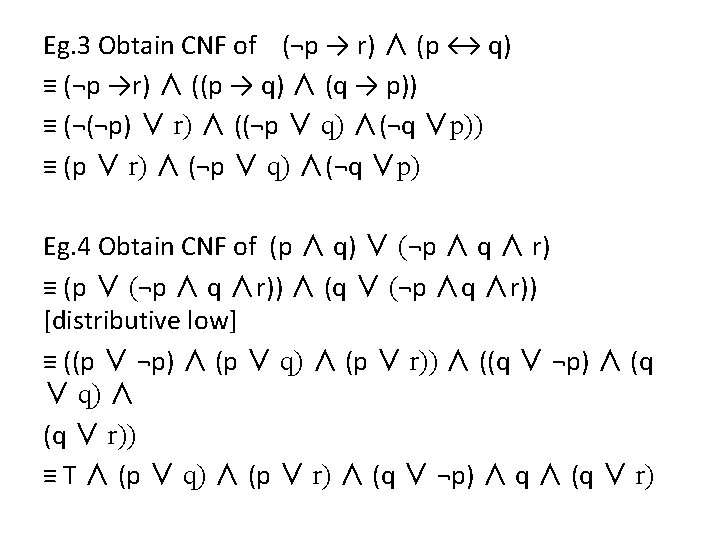



















- Slides: 99

Discrete Mathematics Unit 1 Set Theory and Logic Prof. Mrinali M. Bhajibhakare

Introduction to Discrete Mathematics • Continuous mathematics: Ø It considers objects that vary continuously. Eg. 1 Analog wristwatch(separate hours, minutes, second hands) From an analog watch perspective, between 1: 25 pm and 1: 26 pm there are infinitely many possible different times as the second hand moves around the watch face. Eg. 2. Real number system- core of continuous mathematics(models and tools for analyzing real world phenomena that change smoothly overtime(differential equation) 2

Introduction to Discrete Mathematics • Discrete Mathematics Ø It considers objects that vary in discrete way. Eg. 1 Digital wristwatch : In a digital watch, there are only finitely many possible different times between 1: 25 pm & 1: 26 pm. A digital watch does not show split seconds : - no time between 1: 25: 03 & 1: 25: 04. The watch moves from one time to the next. Eg. 2. Integers: core of discrete mathematics. (models and tools for analyzing real world phenomena that change discretely over time and therefore ideal for studying. Eg. 3. Computers are digitals(numbers are as finite bit strings , data structures, all discrete)

Applications of discrete mathematics • • • Theoretical Computer Science Information Theory Mathematical logic Set theory Combinatorics Graph theory Discrete probability theory Number theory Discrete geometry and computational geometry

Applications of discrete mathematics • In number system RSA(Rivest-Shamir-Adlman) and Public key cryptography. • In graphs and networks-routing problems, maximum flow problems, designing computers, phones, road networks. • In network security • In probability

Sets • Sets- it is defined as any collection of distinct and distinguishable objects. • The objects belonging to sets are called element or members of set. • Objects of the set can be number, alphabets, names, etc. • Eg- 1 -Set of numbers 2 -Set of capitals of states 3 -Set of stationary used by any students 4 -The set of all Indians. 5 - A bouquet of flowers.

Notations • A set is denoted by capital letters of english alphabets A, B, C ……… • Elements of set are denoted by small letters a, b, c…. • If x is an element of set A then we write , x ε A [read as x belongs to A ] • If x is not an element of the set A then we write x ∉ A [read as x does not belongs to A]. • If A is set then |A| stands for number of elements in the set A.

Representation of a set • There are various ways of describing a set: 1. Listing method 2. Statement form 3. Set builder notation 1. Listing method: In this method, the elements are listed within brackets Eg. A={pencile, pen, 5} B={2, 4, 6, 8 ----} 8

Representation of a set 2. Statement form: A statement describing the set, especially where the elements share a common characteristic. Eg. 1. The set of all equilateral triangle 2. The set of all prime ministers of India 3. Set builder notation: It is not always possible or convenient to describe a set by the listing method or the statement form

Representation of a set • A more precise way of describing the set is to specify the property shared by all the elements of the set. • This property is denoted by P(x), • where p is a statement concerning an element x of the set. The set is then simply written as{ x| p(x)} where, { } denote the clause “the set of”. and slash or stroke ‘ |‘ or : denotes “such that”. eg. A={x|x>10} i. e. A is a set of all x such that x is greater than 10

Types of sets 1. Null set(empty set or void set): A set having no element is called an empty set. It is denoted by { } or Ø. Eg. A= {x|x is an even number not divisible by 2} B={x|x is an immortal man} 2. Singletone set: A set having a single element is called a single tone set. Eg. A= {x|x is present president of India} B={5}

Types of sets 3. Finite set: A set having a finite number of elements is called a finite set. Elements of a finite set can be counted. Eg. A={1, 3, 5, 7, 9} is a finite set with 5 elements. B= Ø is a finite set with zero number of elements. 4. Infinite set: A set having an infinite number of elements called as infinite set. Elements of an infinite set cannot be counted. Eg. A={x|x is a natural number} B={x|x is a set of all lines passing through origin}

5. Subset: Ø Set A is said to be a subset of set B if each element of set A is also an element of set B. Ø It is represented as A c B. Ø B is called as superset of A. Ø If A c B then x ε A and x ε B Eg. A={2, 3, 4} & B={2, 3, 4, 5} Then write A c B. 6. Proper subset : Set A is said to be a proper subset of a set B ifa)Every element of set A is an element of set B. b)Set B has at least one element which is not an element of set A. Ø It is represented as A c B. Eg. Let A={1, 2, 3} & B={1, 2} then B c A

Eg if A={1, 3, 5} , B={1, 5} Then B is a proper subset of A. if A={1, 3, 5} , B={1, 3, 5} Then B is subset of A.

7. Comparable set: Two sets A & B said to be comparable if either of these happens: a) A c B b) B c A c) A = B 8. Universal set : Any set which is superset of all the sets under consideration is known as the universal set. It is denoted by S or U. 9. Power Set: The set of all the subsets of a given set A is said to be the power set of A & is expressed as P(A). • if a set B ε P(A) then B c A. • φ ε P(A). • A ε P(A).

Eg. 1. If A={2} then P(A)={ φ , {2}}. 2. if A ={1, 2} then P(A)={φ, {1}, {2}, {1, 2}} • If A has n elements then P(A) has 2 n elements.

10. Equality of sets: Two sets A & B are equal if A is a subset of B and B is also a subset of A, i. e. A c B and B c A implies A = B. Eg. A={BASIC, COBOL, PASCAL} B={PASCAL, COBOL, BASIC} Then A=B Some special sets for numbers: N – the set of all natural numbers {1, 2, 3 ……. . } Z - the set of all integers{…. . -2, -3, -1, 0, 1, 2, 3 ……. . } Z+ - the set of all positive integers{0, 1, 2, 3 ……. . } Q – the set of rational number. Q+ - the set of non negative rational number. R- the set of real number. R+ - the set of positive real number.

Types of sets (Advanced) 1. Bounded and unbounded sets: Set is called bounded , if it is of finite size, conversely, a set which is not bounded is called unbounded. 2. Finite and infinite sets: Finite set has finite number of elements. A set is infinite if it is not finite. 3. Countable and uncountable sets: A set is countable if: (1) it is finite, or (2) it has the same cardinality (size) as the set of natural numbers. Equivalently, a set is countable if it has the same cardinality as some subset of the set of natural numbers. Otherwise, it is uncountable.

Set Operations • Set Union(A∪B) • The union of sets A and B (denoted by A∪B) is the set of elements which are in A, in B, or in both A and B. Hence, A∪B={x|x∈A OR x∈B}. • Example − If A={10, 11, 12, 13} and B = {13, 14, 15}, then A∪B={10, 11, 12, 13, 14, 15}. (The common element occurs only once)

Eg 1 If A ={ n | n ε N , 4< n< 12} B={n | n ε N , 8 < n <15} There fore A={ 5, 6, 7, 8, 9, 10, 11} B={9, 10, 11, 12, 13, 14} Then A U B ={5, 6, 7, 8, 9, 10, 11, 12, 13, , 14} Eg 2 If A={φ} B={a, φ, {φ}) Then AUB = {φ , a, {φ}} = B Note that AU φ =A AU U = U A U A = U

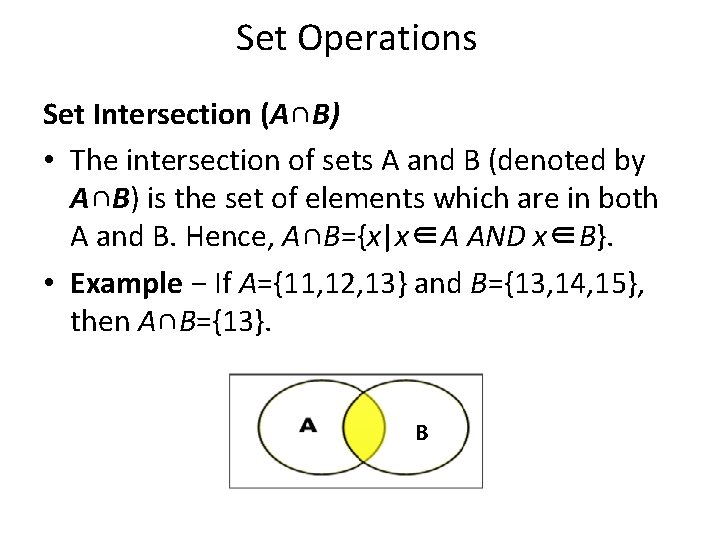
Set Operations Set Intersection (A∩B) • The intersection of sets A and B (denoted by A∩B) is the set of elements which are in both A and B. Hence, A∩B={x|x∈A AND x∈B}. • Example − If A={11, 12, 13} and B={13, 14, 15}, then A∩B={13}. B


Set Operations Complement of a Set (A′, A ) • The complement of a set A (denoted by A′, A) is the set of elements which are not in set A. Hence, A′={x | x∉A}. • More specifically, A′=(U−A) where U is a universal set which contains all objects. • Example − If A={x|x belongs to set of odd integers} then A′={y|y does not belong to set of odd integers}

Eg. If U=N={1, 2, 3, 4, 5} E={2, 3, 6} Then E = {1, 4, 5} Note Φ = U U = Φ

Set Operations Set Difference/ Relative Complement (A – B) • The set difference of sets A and B (denoted by A–B) is the set of elements which are only in A but not in B. Hence, A−B={x|x∈A AND x∉B}. • Example − If A={10, 11, 12, 13} and B={13, 14, 15}, then (A−B)={10, 11, 12} and (B−A)={14, 15}. Here, we can see (A−B)≠(B−A)

Eg. suppose U=N={1, 2, 3, ……. . }, the positive integers. Let A={1, 2, 3, 4}, B={3, 4, 5, 6, 7}, C={6, 7, 8, 9} and let E={2, 4, 6, 8, ……. }, the even integers Then. A =? B =? C =? A-B=? B-C=? B-A=?

Solution: A = {5, 6, 7, 8, 9} B = {1, 2, 8, 9} C = {1, 2, 3, 4, 5} A-B= {1, 2} B-C= {3, 4, 5} B-A={5, 6, 7}

Symmetric Difference(A � B) • The symmetric difference of two sets A and B , denoted by A �B , is defined as – A � B = {x | x ∈ (A-B) or x ∈ (B-A) } In other word A � B =(A-B) ∪ (B-A)

Eg. 1 If A={a, b, e, g} B={d, e, f, g} Then (A � B)= {a, b, d, f} Eg. 2 if A={2, 4, 5, 9} B={x ∈ Z+ | X 2 <=16 } then (A � B)=?

A={2, 4, 5, 9} B={0, 1, 4, 9, 16} Then A-B={2, 5} B-A={0, 1, 16} As we know (A � B)= (A-B)U(B-A) (A � B)={2, 5, 0, 1, 16}

Set Operations Cartesian Product / Cross Product (A X B) • The Cartesian product of n number of sets A 1, A 2, …An denoted as A 1×A 2⋯×An can be defined as all possible ordered pairs (x 1, x 2, …xn) where x 1∈A 1, x 2∈A 2, …xn∈An • Example − If we take two sets A={a, b} and B={1, 2}, • The Cartesian product of A and B is written as − A×B={(a, 1), (a, 2), (b, 1), (b, 2)} • The Cartesian product of B and A is written as − B×A={(1, a), (1, b), (2, a), (2, b)}

Eg. If A= {1}, B={a, b}, C={2, 3} find 1. AXB =? 2. BXA=? 3. A 2 4. B 2

• Solution: A= {1}, B={a, b}, C={2, 3} 1. AXB = {(1, a), (1, b)} 2. BXA={(a, 1), (b, 1)} 3. A 2 ={(1, 1)} 4. B 2={(a, a), (a, b), (b, a), (b, b)}

cardinality of set • Cardinality of a set S, denoted by |S|, is the number of elements of the set. The number is also referred as the cardinal number. If a set has an infinite number of elements, its cardinality is ∞. • Example − |{1, 4, 3, 5}|=4, |{1, 2, 3, 4, 5, …}|=∞ • If there are two sets X and Y, • |X|=|Y| denotes two sets X and Y having same cardinality. It occurs when the number of elements in X is exactly equal to the number of elements in Y. • |X|≤|Y| denotes that set X’s cardinality is less than or equal to set Y’s cardinality. It occurs when number of elements in X is less than or equal to that of Y. • |X|<|Y| denotes that set X’s cardinality is less than set Y’s cardinality. It occurs when number of elements in X is less than that of Y.

Laws of set theory 1. Commutativity: a) A U B = B U A b) A ᴒ B = B ᴒ A 2. Associativity: a)A U (BUC)=(A U B) U C b)A ᴒ (B ᴒ C)= (A ᴒ B) ᴒ C 3. Distributivity : a) A U (B ᴒ C)= (A U B) ᴒ (AU C) b) A ᴒ (B U C) = (A ᴒ B) U (A ᴒ C)

Laws of set theory 4. Idempotent laws: a) A U A =A b) A ᴒ A=A 5. Absorption laws: a) A U (A ᴒ B)= A b) A ᴒ (A U B)=A 6. De-morgan’s law: a) AU B = A ᴒ B b) A ᴒ B = A U B

Addition principle • Let A and B be finite set which are disjoint(no common element) then |AUB| = |A|+|B| Proof: If A or B is empty set then proof is trivial. Hence let us assume that A ≠ Φ , B ≠ Φ Since A & B are finite disjoint sets, Let A={a 1, a 2, a 3……am} B={b 1, b 2, b 3………bn} Where ai ≠ bj for 1<=i<=m , 1<=j<=n, |A|=m and |B|=n then AUB={a 1, a 2, a 3…. am, b 1, b 2, b 3. . . bn} i. e. AUB contains exactly m+n elements hence |AUB|=m+n=|A|+|B| hence proved

Principal of Inclusion and exclusion • Let A & B be finite set then – |A U B| =|A| + |B| - |A ᴒ B| Proof: Consider the venn diagram A ᴒ B A- B is shaded portion We may express AUB as disjoint union of two sets, by writing. AUB = (A-B) U B

Principal of Inclusion and exclusion Hence by the addition principle, |A U B| = |A- B| + |B| = |A|- |A ᴒ B| + |B| [ by property] Hence |A U B| =|A| + |B| - |A ᴒ B|

Multiset • It is generalization of set, it is collection of distinct objects. • In multiset, an object can occur more than once. Eg- the collection of books in a library can contain multiple copies of the same books such a collection is multiset. • It is also called as bags, heap or bunch or weighted set.

Multiset • To distinguish a set and a multiset, we denote the letter by enclosing the elements within square brackets eg. [a , b , a] is m set. • Multiplicity of Mset: Ø Multiplicity of mset is defined as the number of times the elements appears in the mset. Thus in the mset [a, b, a, a] multiplicity of a is 3 while multiplicity of b is 1. Ø If an element does not belongs to mset, its multiplicity is zero.

Multiset • We can characterize a multiset as a pair (A, µ) where A is the generic set and µ is the multiplicity function defined as µ : A {1, 2, 3, ……. } So that µ(a)=k where k is the number of times the element a occur in the mset. Eg. If [a, b, c, c, a, c] is the mset µ(a)=2, µ(b)=1, µ( c)=3.

Mset operations 1. Equality of mset: If number of occurrences of each element is the same in both the msets, then the msets are equal. Eg [a, b, a, a]=[a, a, b, a] However [a, b, a]≠ [a, b] 2. Multisubset(msubset): A multiset A is said to be a multi subset of B if multiplicity of each element in A is less or equal to its multiplicity in B. Eg A=[1, 2, 2, 3] B=[1, 1, 1, 2, 2, 3] Therefore A C B

Mset operations 3. Union of mset: If A & B are two msets, then AUB is the mset such that for each element x ∈ AUB, µ(x)=max[µA (x), µB (x)] Eg A=[a, b, b, c], B=[b, c, c, d] Then AUB=[a, b, b, c, c, d] 4. Intersection of Mset: If A & B are two msets then A ∩ B is defined as the mset such that for each element x ∈ A ∩ B, µ(x)=min[µA (x), µB (x)] Eg. A=[1, 1, 1, 2, 2, 3] B=[1, 2, 2, 2, 3, 3] then A ∩ B=[1, 2, 2, 3]
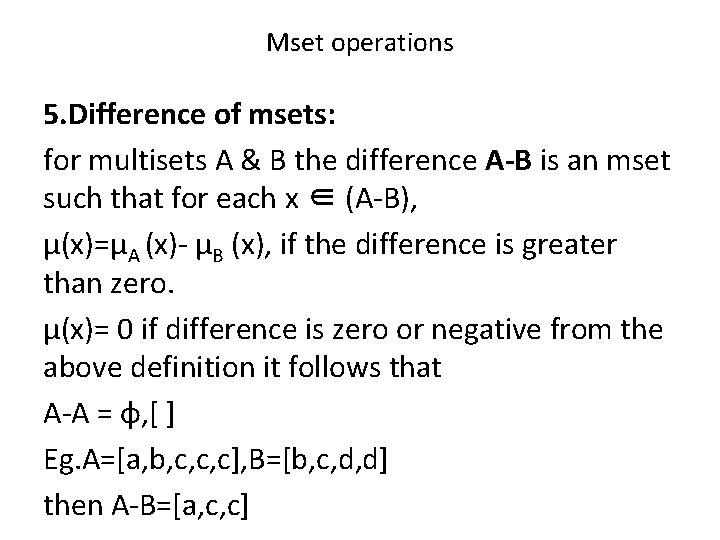
Mset operations 5. Difference of msets: for multisets A & B the difference A-B is an mset such that for each x ∈ (A-B), µ(x)=µA (x)- µB (x), if the difference is greater than zero. µ(x)= 0 if difference is zero or negative from the above definition it follows that A-A = φ, [ ] Eg. A=[a, b, c, c, c], B=[b, c, d, d] then A-B=[a, c, c]

Proposition A proposition is a declarative sentence that is either true or false. Examples of propositions: • 1 + 0 = 1 - T • 0 + 0 = 2 - F • There are seven days in a week - T Examples that are not propositions • Sit down! • What time is it? • x + 1 = 2 • x + y = z • What a beautiful painting !

Propositional Logic Constructing Propositions • Propositional Variables: p, q, r, s, . . . • The proposition that is always true is denoted by T and the proposition that is always false is denoted by F. • Compound Propositions; constructed from logical connectives and other propositions • • • Negation ¬ (NOT) Conjunction ∧ (AND) Disjunction ∨ (OR) Implication → (If -----then) Biconditional ↔ (Iff)

Conjunction • The conjunction of propositions p and q is denoted by p ∧ q and has this truth table: p q p∧q T T F F F T F F • p : The sun is shining q : The birds are singing Then p ∧ q is the statement “ The sun is shining and birds are singing”.

• The words “but” and “while” are treated as equivalent words to “and” Eg. Translate into symbolic form 1. Amar is poor but happy Ans: consider p : Amar is poor, q : Amar is happy, therefore symbolic form is p ∧ q. 2. We watch television while we have dinner Ans: p : we watch television q : we have dinner therefore symbolic form is p ∧ q.

Negation ( ¬ , ~) (NOT) • The negation of a statement is formed either by introducing the word “not” at a proper place or by prefixing the statement with the phrase. ”It is not the case”. P ~p T F F T Eg. if p is a statement “I am going for a walk”. then ~p is the statement. “I am not going for a walk”. or “it is not the case that I am going for a walk”. Eg. If q is a statement “ 3 is not a prime number” ~q= “ ? “

Disjunction (∨) (OR) • The disjunction of propositions p or q is denoted by (p ∨ q )and has this truth table: p q p ∨q T T F F F Eg. there is an error in the program or data is wrong Ans: Let p: there is an error in the program. q : the data is wrong symbolic form is p ∨ q.

Disjunction • In previous example, the connective “or” is used in the inclusive sense i. e. at least one possibility exists or even both possibilities are exist. Eg. Either I will read a book or go to sleep. ans: let p: I will read a book. q: I will go to sleep. symbolic form is p ∨ q. • In this example, the connective “or” is used in the exclusive sense i. e. either one or other activity can happen , but not both. • In logic, ∨ this symbol is used in inclusive sense. and ∨ this symbol is used in exclusive sense.

Implication/Conditional → (If -----then) • If p and q are propositions, then compound statement “if p, then q”, denoted by p → q is called conditional statement and has this truth table: p q p →q T T F F F T T F F T • In p → q, p is the hypothesis (antecedent or premise) and q is the conclusion (or consequent). • Implication can be expressed by disjunction and negation: p → q ≡ ¬p ∨ q

Understanding Implication • Different Ways of Expressing p → q : if p, then q p implies q if p, q p only if q q unless ¬p q when p q if p q whenever p p is sufficient for q q follows from p q is necessary for p a necessary condition for p is q a sufficient condition for q is p

Converse, Contrapositive, and Inverse • q → p is the converse of p → q • ¬q → ¬p is the contrapositive of p → q • ¬p → ¬q is the inverse of p → q • Example: Find the converse and contrapositive of“If it rains then I carry an umbrella”. Solution: p → q let p: It rains q : I carry an umbrella. • converse: (q → p) If I carry an umbrella then it rains • contrapositive: (¬q → ¬p) if I do not carry an umbrella then it does not rains ,

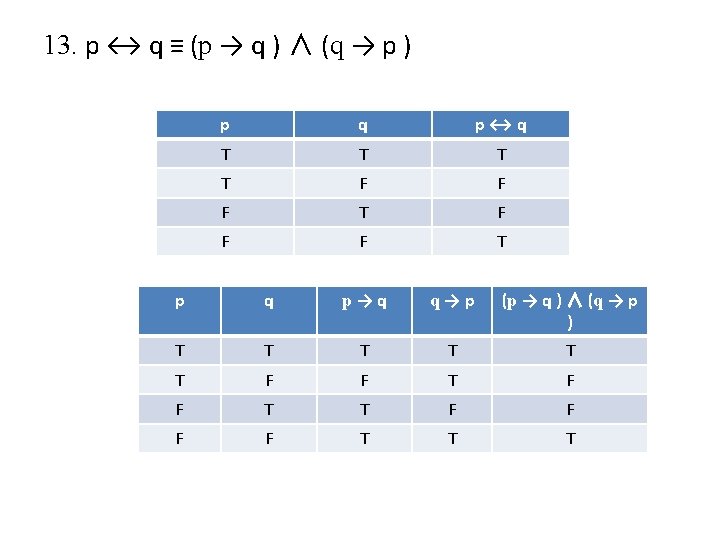
Biconditional ↔ (If and only if) • If p and q are propositions, then the biconditional proposition p ↔ q has this truth table p q p ↔q T T F F F T p ↔ q also reads as p if and only if q (p iff q). p is necessary and sufficient for q if p then q, and conversely p implies q, and vice-versa Eg. An integer is even if and only if it is divisible by 2

Precedence of Logical Operators • ¬ • ∧ • ∨ • → • ↔ Thus p ∨ q → ¬r is equivalent to (p ∨ q) → ¬r. If the intended meaning is p ∨ (q → ¬r) then parentheses must be used.

Satisfiability, Tautology, Contradiction • A proposition is satisfiable, if its truth table contains true at least once. Example: p ∧ q. • a tautology, if it is always true. Example: p ∨ ¬p. • a contradiction, if it always false. Example: p ∧ ¬p. • a contingency, if it is neither a tautology nor a contradiction.

Logical Equivalence • Two statement forms are said to be logically equivalent if both have the same truth values. • This is written as p ≡ q. • It is easy to show: • Fact p ≡ q if and only if p ↔ q is a tautology.

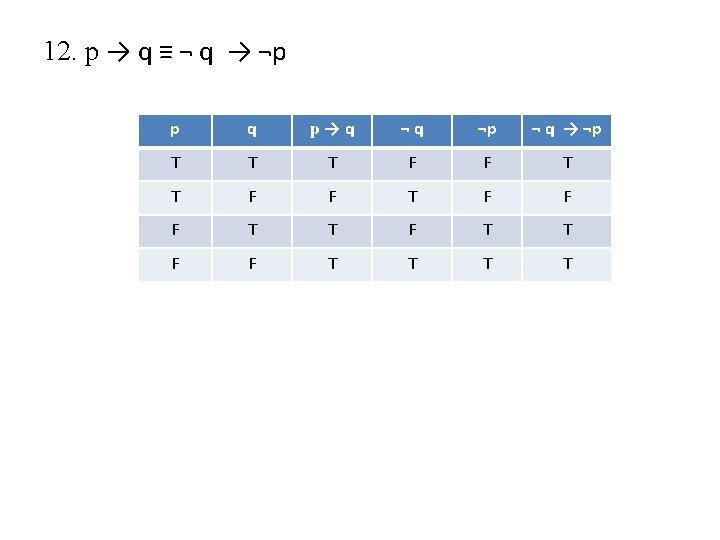
• p → q and ¬q → ¬p are logically equivalent p q ¬p ¬q (p → q ) (¬q → ¬p ) T T F F F T T F F T T note that last two column are identical hence p → q and ¬q → ¬p are logically equivalent.

Basic logical equivalence 1. Idempotence law: i) p ∨ p ≡ p. ii) p ∧ p ≡ p 2. Commutative : i) p ∨ q ≡ q ∨ p ii) p ∧ q ≡ q ∧ p P p∨p T T F F P p∧p T T F F
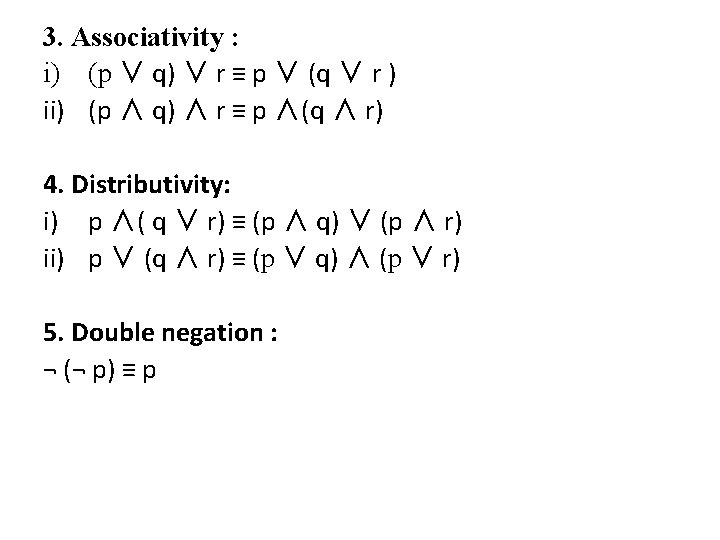
3. Associativity : i) (p ∨ q) ∨ r ≡ p ∨ (q ∨ r ) ii) (p ∧ q) ∧ r ≡ p ∧(q ∧ r) 4. Distributivity: i) p ∧( q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) ii) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) 5. Double negation : ¬ (¬ p) ≡ p

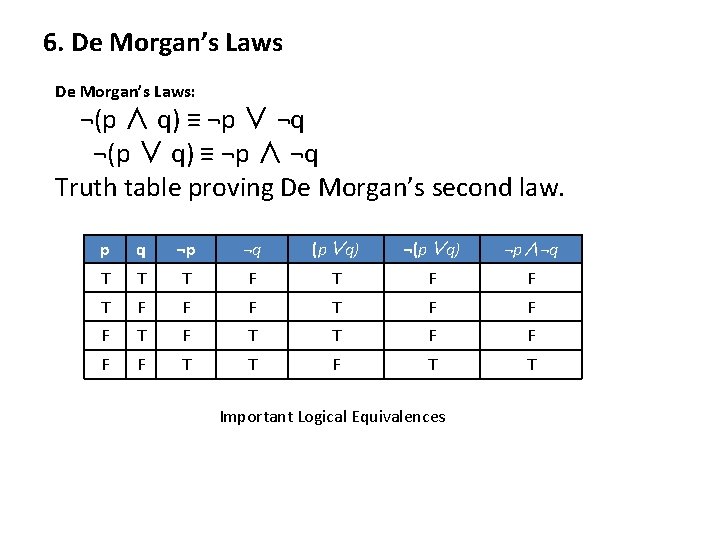
6. De Morgan’s Laws: ¬(p ∧ q) ≡ ¬p ∨ ¬q ¬(p ∨ q) ≡ ¬p ∧ ¬q Truth table proving De Morgan’s second law. p q ¬p ¬q (p∨q) ¬p∧¬q T T T F F F T T F T T Important Logical Equivalences

Some other properties 7. i)(p ∨ T) ≡ T ii)(p ∧ T) ≡ p 8. i) (p ∨ F) ≡ p ii) (p ∧ F) ≡ F 9. i) (p ∨ ¬ p) ≡ T ii) (p ∧ ¬ p) ≡ F

10. i) ¬ T ≡ F ii) ¬ F ≡ T 11. Law of absorption : i) p ∨ (p ∧ q) ≡ p ii) p ∧ (p ∨ q) ≡ p P q (p ∧ q) p ∨ (p ∧ q) T T T F F F



14. p → q ≡ ¬p ∨ q 15. p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬ q) Eg. show that (¬p) → (p → q ) is a tautology. p q ¬p (p → q ) (¬p) → (p → q ) T T F T T T F F F T T T T F F T T T column (¬p) → (p → q ) is always true and hence it is tautology

• Using laws of algebra proposition prove equivalence (p ∨ q) ∧ ¬p ≡ ¬p ∧ q L. H. S. ≡ (p ∨ q) ∧ ¬p ≡ (p ∧ ¬p) ∨(q ∧ ¬p) [ Distributivity] ≡ F ∨(q ∧ ¬p) [p ∧ ¬p ≡ F] ≡ (q ∧ ¬p) [F ∨ p ≡ p] ≡ ¬p ∧ q [commutativity] ≡ R. H. S

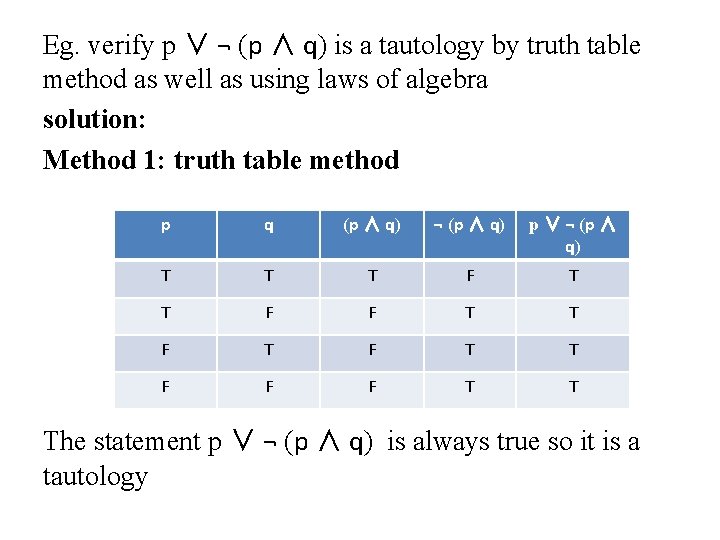
Eg. verify p ∨ ¬ (p ∧ q) is a tautology by truth table method as well as using laws of algebra solution: Method 1: truth table method p q (p ∧ q) ¬ (p ∧ q) p ∨ ¬ (p ∧ q) T T T F F T T F F F T T The statement p ∨ ¬ (p ∧ q) is always true so it is a tautology

• Method II : using laws of algebra p ∨ ¬ (p ∧ q) ≡ p ∨ (¬ p ∨ ¬ q) [Demorgan’s law] ≡ (p ∨ ¬ p ) ∨ (¬ q) [Associativity] ≡ T ∨ ¬ q [(p ∨ ¬ p ) ≡ T] ≡ T [T ∨ p ≡ T] hence , p ∨ ¬ (p ∧ q) is a tautology

Normal forms • Disjunctive normal forms(DNF)(OR- ∨ / sum) • Conjunctive normal forms(CNF) (AND- ∧/product) 1. Disjunctive normal forms(DNF)(OR- ∨ / sum): In a logical expression – • A product of variable and their negation is called an elementary product. eg. p ∧ q, ¬ p ∧ ¬ q, ¬ p ∧ q are elementary product. • A sum of variable and their negation is called elementary sum. eg p ∨ q, ¬ p ∨ ¬ q , ¬ p ∨ q are elementary sum.

Disjunctive normal forms(DNF)(OR- ∨ / sum): • A logical expression is said to be in disjunctive normal form if it is the sum of elementary product. • procedure to obtain DNF from a logical expression 1. Remove all conditional(→) and biconditional(↔) by an equivalent expression containing ∧, ∨, ¬ only. 2. Eliminate ¬ before sum and product by using the double negation or by using De-morgan’s law. 3. Apply the distributive law until sum of elementary product is obtained.

Eg. 1. p ∧ (p → q) obtain DNF solution: ≡ p ∧ (¬p ∨ q) [property 14] ≡ (p ∧ ¬p ) ∨ (p ∧ q) [distributive law] ≡ F ∨ (p ∧ q) is required dnf 2. obtain dnf forp ∨(¬p → (q ∨ (q → ¬ r)) solution: ¬ ≡ p ∨(¬p → (q ∨ (¬ q ∨ ¬ r)) ≡ p ∨(p ∨ (q ∨ (¬ q ∨ ¬ r)) ≡ p ∨ q ∨ ¬ r ≡ p∨ q ∨ ¬ r which is required dnf [Idempotance law]

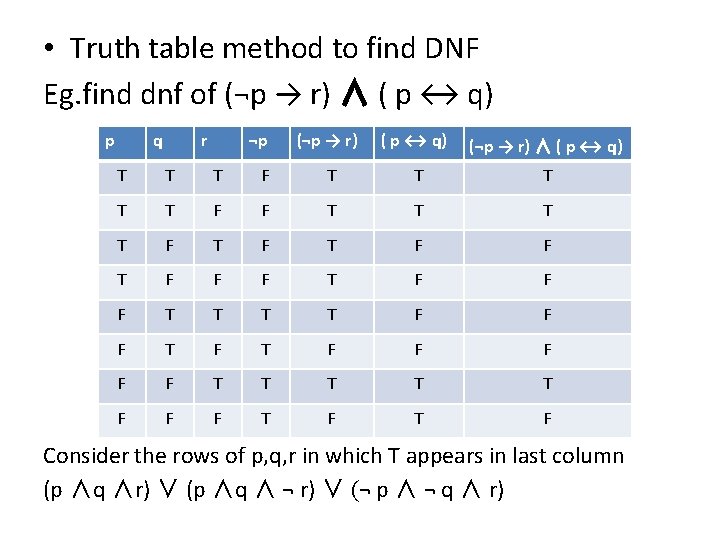
• Truth table method to find DNF Eg. find dnf of (¬p → r) ∧ ( p ↔ q) p q r ¬p (¬p → r) ( p ↔ q) (¬p → r) ∧ ( p ↔ q) T T T F F T T F T F F F T T F F F T T T F F F T F Consider the rows of p, q, r in which T appears in last column (p ∧q ∧r) ∨ (p ∧q ∧ ¬ r) ∨ (¬ p ∧ ¬ q ∧ r)

Eg 3. Obtain DNF of (p ∧(p → q)) → q Eg. 4 obtain DNF of ¬(p →(q ∧r))


Conjunctive normal forms(CNF) (AND- ∧/product) • A logical expression is said to be in conjunctive normal form if it consist of a product of elementary sum. eg. 1. p ∧ (p → q) obtain cnf ≡ p ∧ (¬p ∨ q) which is required cnf eg. 2 (¬p ∧ q) ∨ q ≡ (¬p ∨ q) ∧ (q ∨ q) ≡ (¬p ∨ q) ∧ q which is required cnf

Eg. 3 Obtain CNF of (¬p →r) ∧ (p ↔ q) Eg. 4 Obtain CNF of (p ∧ q) ∨(¬p ∧ q ∧ r)
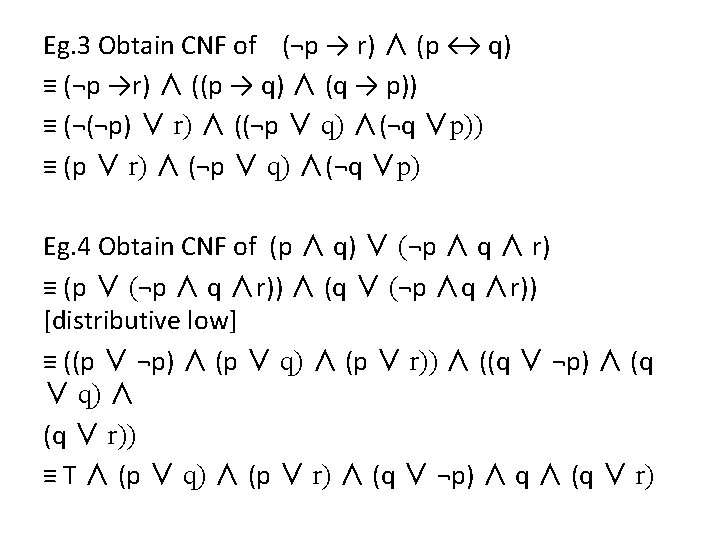

Predicates • Consider the following sentences 1. “x is tall and handsome” 2. “x+3=5” 3. “x+y>= 10” These sentences are not propositions, since they do not have any truth value, however if values are assigned to the variables, each of them become propositions which is either true or false • The above eg can be converted into 1. He is tall and handsome 2. “ 2+3=5” (true statement) 3. “ 2+3>=10” (false statement)

• An assertion that contain one or more variable is called a predicates, its truth value is predicated after assigning truth values to its variable. • Eg 1 & 2 are 1 place predicate • Eg 3 is two place predicate • If predicate p containing n variables then it is called as n-place predicate. • Eg. 1. ” x is a city in india” is denoted by p(x) • Eg. 2. “x is father of y” is denoted by p(x, y) • Collective values of variables which represent set called as universe of discourse. • When we specify value for a variable appearing in a predicate we bind that variable

• Consider the eg. Eg 1 p(x): x+3=5 Let the universe of discourse be the set of all integers , binding x by putting x=2 we get true proposition. Eg 2 p(x, y): x+y=10 Let the universe of discourse be the set of natural number If we put x=1 and y=9 then we get p(1, 9) i. e. true propositions Therefore method of binding individual variable in a predicate is quantification of the variable

Universal quantifier (Ɐ)(for all /for every) • If p(x) is predicate with the individual variable x as an argument , then the assertion “for all x , p(x) “ which is interpreted as “for all values of x, the assertion p(x) is true” is a statement in which variable x is said to be universally quantified. • We denote the phrase “for all” by Ɐ, called universal quantifier. • If p(x) is true for every possible value of x the Ɐ x p(x) is true

• Eg let p(x) be predicate “x>=0”; where x is any positive integer then the proposition Ɐ x p(x) is true , however if x is any real number the Ɐ x p(x) is false proposition.

Existential quantifier(ⱻ)(there exists) • Suppose for the predicate p(x), Ɐ xp(x) is false, but there exists at least one value of x for which p(x) is true, then we say that in this proposition x is bound by existential quantification. • We denote words “there exists” by symbol ⱻ. • Then the notation ⱻ x p(x) means “there exists a value of x(in the universe of discourse) for which p(x) is true”. eg. Let p(x) be the predicate “x+3=5” and let the universe of discourse be the set of integers then the proposition ⱻ x p(x) is true (for x=2) but Ɐ xp(x) is false

Negation of quantified statement Statement its negation Ɐ x (p(x)) ⱻ x (¬ p(x) ) ⱻ x(¬ p(x)) Ɐ x (p(x)) Ɐ x (¬ p(x)) ⱻ x( p(x)) Ɐ x (¬ p(x))

Method of proofs • Laws of inference(conclusion reached on the basis of evidence & reasoning) Definition: A valid argument is a finite sequence of statements P 1, P 2, -----Pn called premices together with a statement C called conclusion such that P 1 ∧ P 2 ∧P 3 ----- ∧ Pn → C is a tautology. This concept is used in the following methods 1. Modus Ponens (Law of detachment) This rule is presented in the following form p → q p q

• The assertion above the horizontal line are called premises (or hypothesis). • The assertion below line is called conclusion. • This rule constitute a valid argument since (p ∧ (p → q)) → q is a tautology. Eg. If suresh gets a first class, he will get a job easily. suresh gets a first class therefore he will get a job easily. Solution: let p: suresh gets a first class q: Suresh will get a job easily. Then the premises are p → q and p , the conclusion is q. Inferential form is thus- p→q p q Hence this form of argument is valid

2. Moduse tollens(law of contraposition): This rule is presented in the following form p → q ¬ p This argument is valid since (p → q) ∧ ¬ q → ¬ p is a tautology. eg. If suresh gets a first class, he will get a job. Suresh does not get a job. therefore suresh does not get a first class solution: let p: Suresh gets a first class q: Suresh gets a job then inferential form is – p → q ¬ p hence the above argument is valid

3. Disjunctive syllogism: The rule of inference is presented in the form p ∨ q ¬ p q note that (p ∨ q ) ∧ ¬ p → q is a tautology. eg. either it is raining or it is windy, It is not raining. therefore it is windy. solution: let p: it is raining q: it is windy then inferential form is p ∨ q ¬ p q then the argument is valid

4. Hypothetical syllogism: (chain rule) rule is in the form of p → q q → r p → r note that (p → q) ∧ (q → r) → (p → r) is a tautology hence the above argument is valid argument

Mathematical Induction It is an approach where we can generalize a solution. It is used to establish correctness of a statement involving natural numbers. • Proof of mathematical induction consist of three basic steps. If the statement p is to be proved then 1. Show that p is true for some particular integer n 0 , this is called the basis. 2. assume p is true for some particular integer (k>= n 0 ) this is called induction hypothesis. 3. prove p is true for n= k+1, is called as induction step.

eg. 1 state the principle of mathematical induction and prove the following proposition: 1+4+7+----+(3 n-2)= n(3 n-1)/2 solution: let p(n) : 1+4+7+----+(3 n-2)= n(3 n-1)/2 step 1: Basis of induction for n=1, p(1) : 1 = 1(3 -1)/2=1 therefore p(1) is true for n=1 step 2: Induction hypothesis Assume p(n) is true of n=k i. e. p(k) = 1+4+7+----+(3 k-2) = k(3 k-1)/2 is true.

step 3 : Induction step given that p(k)is true , we check the correctness of statement for k+1 p(k+1) : 1+4+7+------+(3 k-2)+(3(k+1)-2) = k+1(3(k+1)-1))/2 L. H. S: 1+4+7+------+(3 k-2)+(3(k+1)-2) =k(3 k-1)/2 + (3(k+1)-2) = k(3 k-1)/2 + 3 k+3 -2 = k(3 k-1)/2 + 3 k+1 = (3 k 2 -k + 6 k+2)/2 = (3 k 2 + 5 k+2)/2 = (k+1)(3(k+1)-1)/2 = R. H. S hence proved

eg 2. by using mathematical induction prove that 13 + 23 +-----n 3 = n 2 (n+1)2 /4 solution: let p(n) : 13 + 23 +-----n 3 = n 2 (n+1)2 /4 step 1: basis of induction for n=1 p(1): 13 = 12(1+1) 2 /4 =4/4=1 therefore p(1) is true Step 2: Induction hypothesis assume p(n) is true for n=k p(k) : 13 + 23 +-----k 3= k 2 (k+1)2 /4 is true

step 3: Induction step given that p(k) is true, we have to prove that p(k+1) is true therefore L. H. S : p(k+1)= 13 + 23 +-----k 3+ (k+1) 3 = (k+1) 2 (k+2) 2 / 4 = k 2 (k+1)2 /4 +(k+1) 3 = k 2 (k+1)2 + 4(k+1) 3 /4 =(k+1) 2[k 2 +4(k+1)]/4 =(k+1) 2[k 2 +4 k+4]/4 = (k+1) 2[(k+2)]/4 = (k+1) 2 (k+2) 2 /4 =R. H. S hence proved

eg 3. 1+3+5+------+(2 n-1)= n 2 for n =1 prove above statement by M. I.

1+3+5+------+(2 n-1)= n 2 let p(n) : 1+3+5+------+(2 n-1)= n 2 step 1. basis of induction for n=1 , (2 -1)= 12 =1 Step 2: Induction hypothesis assume p(n) is true for n=k 1+3+5+------+(2 k-1)= k 2 is true. step 3: Induction step given that p(k) is true, we have to prove that p(k+1) is true therefore 1+3+5+------+(2 k-1)+(2(k+1)-1)= (k+1)2 = k 2+(2(k+1)-1) =k 2+(2 k+2 -1) =k 2+(2 k+1) =(k+1) = (k+1)2 =R. H. S