Discrete Mathematics Relation Cartesian Product If A 1

Discrete Mathematics Relation

Cartesian Product If A 1, A 2, …, Am are nonempty sets, then the Cartesian Product of these sets is the set of all ordered m-tuples (a 1, a 2, …, am), where ai Ai, i = 1, 2, … m. p Denoted A 1 A 2 … Am = {(a 1, a 2, …, am) | ai Ai, i = 1, 2, … m} p

Cartesian Product Example If A = {1, 2, 3} and B = {a, b, c}, find A B p A B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)} p

Subsets of the Cartesian Product Many of the results of operations on sets produce subsets of the Cartesian Product set p Relational database p n n n Each column in a database table can be considered a set Each row is an m-tuple of the elements from each column or set No two rows should be alike

Using Matrices to Denote Cartesian Product p p For Cartesian Product of two sets, you can use a matrix to find the sets. Example: Assume A = {1, 2, 3} and B = {a, b, c}. The table below represents A × B. a b c 1 (1, a) (1, b) (1, c) 2 (2, a) (2, b) (2, c) 3 (3, a) (3, b) (3, c)

Cardinality of Cartesian Product The cardinality of the Cartesian Product equals the product of the cardinality of all of the sets: | A 1 A 2 … Am | = | A 1 | | A 2 | … | A m |

Subsets of the Cartesian Product Many of the results of operations on sets produce subsets of the Cartesian Product set p Relational database p n n n Each column in a database table can be considered a set Each row is an m-tuple of the elements from each column or set No two rows should be alike

Introduction p Given two sets X and B, its Cartesian product Xx. Y is the set of all ordered pairs (x, y) where x X and y Y n p In symbols Xx. Y = {(x, y) | x X and y Y} A binary relation R from a set X to a set Y is a subset of the Cartesian product Xx. Y n n Example: X = {1, 2, 3} and Y = {a, b} R = {(1, a), (1, b), (2, b), (3, a)} is a relation between X and Y

Domain and range Given a relation R from X to Y, p The domain of R is the set n p The range of R is the set n p Dom(R) = { x X | (x, y) R for some y Y} Rng(R) = { y Y | (x, y) R for some x X} Example: n n n if X = {1, 2, 3} and Y = {a, b} R = {(1, a), (1, b), (2, b)} Then: Dom(R)= {1, 2}, Rng(R) = (a, b}

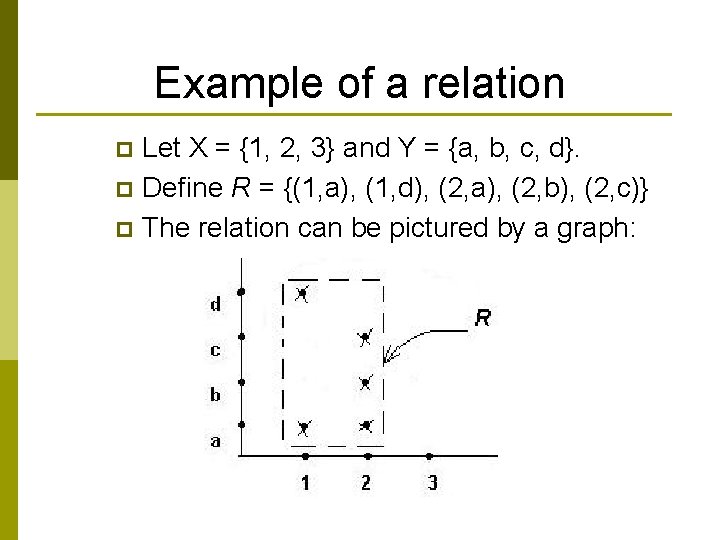
Example of a relation Let X = {1, 2, 3} and Y = {a, b, c, d}. p Define R = {(1, a), (1, d), (2, a), (2, b), (2, c)} p The relation can be pictured by a graph: p

Example A is a set of students and B is a set of courses p A relation R may be defined as “register the course” p Paul Giblock R CSCI 2710 Danny Camper R CSCI 2710

Relation on a Single Set Example A is the set of all courses p A relation R may be defined as the course is a prerequisite p CSCI 2150 R CSCI 3400 p R = {(CSCI 2150, CSCI 3400), (CSCI 1710, CSCI 2910), (CSCI 2800, CSCI 2910), …} p

Matrix of a Relation We can represent a relation between two finite sets with a matrix p MR = [mij], where p mij = 1 if (ai, bj) R 0 if (ai, bj) R

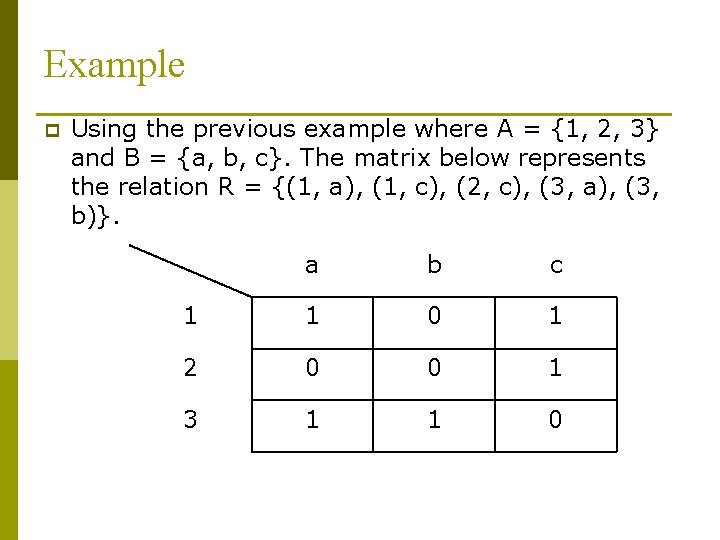
Example p Using the previous example where A = {1, 2, 3} and B = {a, b, c}. The matrix below represents the relation R = {(1, a), (1, c), (2, c), (3, a), (3, b)}. a b c 1 1 0 1 2 0 0 1 3 1 1 0

Digraph of a Relation Let R be a relation on A p We can represent R using a diagram p n n Each element of A is a circle called a vertex If ai is related to aj, then draw an arrow from the vertex ai to the vertex aj In degree means number of arrows coming into a vertex p Out degree means number of arrows coming out of a vertex p

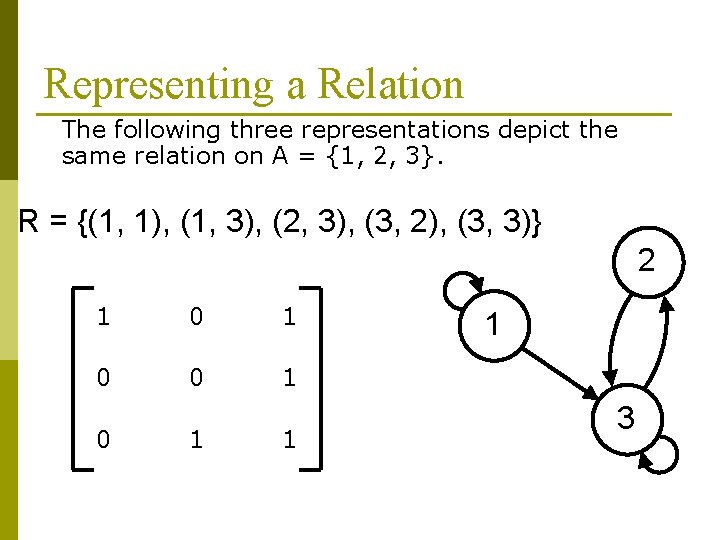
Representing a Relation The following three representations depict the same relation on A = {1, 2, 3}. R = {(1, 1), (1, 3), (2, 3), (3, 2), (3, 3)} 2 1 0 0 1 1 1 3

Properties of relations Let R be a relation on a set X i. e. R is a subset of the Cartesian product Xx. X R is reflexive if (x, x) R for every x X p R is symmetric if for all x, y X such that (x, y) R then (y, x) R p R is transitive if (x, y) R and (y, z) R imply (x, z) R p R is antisymmetric if for all x, y X such that x y, if (x, y) R then (y, x) R p

Partial Order Relations Let X be a set and R a relation on X R is a partial order on X if R is reflexive, anti-symmetric and transitive.

Inverse of a relation Given a relation R from X to Y, its inverse R-1 is the relation from Y to X defined by R-1 = { (y, x) | (x, y) R } q Example: if R = {(1, a), (1, d), (2, a), (2, b), (2, c)} then R -1= {(a, 1), (d, 1), (a, 2), (b, 2), (c, 2)}

Equivalence relations Let X be a set and R a relation on X is an equivalence relation on X R is reflexive, symmetric and p. R transitive.

Equivalence classes Let X be a set and let R be an equivalence relation on X. Let a X. p Define [a] ={ x X | x. Ra }

Matrices of relations Let X, Y be sets and R a relation from X to Y p Write the matrix A = (aij) of the relation as follows: p n n Rows of A = elements of X Columns of A = elements of Y Element ai, j = 0 if the element of X in row i and the element of Y in column j are not related Element ai, j = 1 if the element of X in row i and the element of Y in column j are related

The matrix of a relation (1) Example: Let X = {1, 2, 3}, Y = {a, b, c, d} Let R = {(1, a), (1, d), (2, a), (2, b), (2, c)} The matrix A of the relation R is A= a b c d 1 1 0 0 1 2 1 1 1 0 3 0 0

The matrix of a relation (2) If R is a relation from a set X to itself and A is the matrix of R then A is a square matrix. p Example: Let X = {a, b, c, d} and R = {(a, a), (b, b), (c, c), (d, d), b, c), (c, b)}. Then p p A= a b c a 1 0 0 b 0 1 1 c 0 1 1 d 0 0 0 1

The matrix of a relation on a set X Let A be the square matrix of a relation R from X to itself. Let A 2 = the matrix product AA. p R is reflexive All terms aii in the main diagonal of A are 1. p R is symmetric aij = aji for all i and j, n p i. e. R is a symmetric relation on X if A is a symmetric matrix R is transitive whenever cij in C = A 2 is nonzero then entry aij in A is also nonzero.

Relational databases p A binary relation R is a relation among two sets X and Y, already defined as R X x Y. p An n-ary relation R is a relation among n sets X 1, X 2, …, Xn, i. e. a subset of the Cartesian product, R X 1 x X 2 x…x Xn. n Thus, R is a set of n-tuples (x 1, x 2, …, xn) where xk Xk, 1 < k < n.

Databases A database is a collection of records that are manipulated by a computer. They can be considered as n sets X 1 through Xn, each of which contains a list of items with information. p Database management systems are programs that help access and manipulate information stored in databases. p

Relational database model Columns of an n-ary relation are called attributes p An attribute is a key if no two entries have the same value p n p e. g. social security number A query is a request for information from the database

Operators The selection operator chooses n-tuples from a relation by giving conditions on the attributes p The projection operator chooses two or more columns and eliminates duplicates p The join operator manipulates two relations p

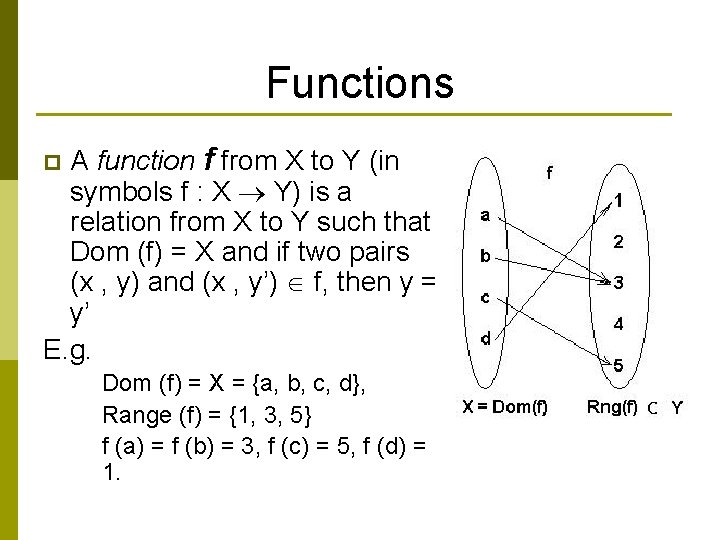
Functions A function f from X to Y (in symbols f : X Y) is a relation from X to Y such that Dom (f) = X and if two pairs (x , y) and (x , y’) f, then y = y’ E. g. p Dom (f) = X = {a, b, c, d}, Range (f) = {1, 3, 5} f (a) = f (b) = 3, f (c) = 5, f (d) = 1.

Domain and Range Domain of f = X n Range of f = { y | y = f (x) for some x X} n A function f : X Y assigns to each x in Dom (f) = X a unique element y in Range (f) Y. n Therefore, no two pairs in f have the same first coordinate. n

One-to-one functions A function f : X Y is one-to-one for each y Y there exists at most one x X with f (x) = y. p Alternative definition: f : X Y is one-to-one for each pair of distinct elements x 1, x 2 X there exist two distinct elements y 1, y 2 Y such that f(x 1) = y 1 and f(x 2) = y 2. p Examples: n 1. The function f (x) = 2 x from the set of real numbers to itself is one-to-one n 2. The function f : R R defined by f (x) = x 2 is not one-to-one, since for every real number x, f (x) = f (-x).

Onto functions A function f : X Y is onto for each y Y there exists at least one x X with f (x) = y, i. e. Range (f) = Y. n Example: The function f (x) = ex from the set of real numbers to itself is not onto Y = the set of all real numbers. However, if Y is restricted to Range (f) = R +, the set of positive real numbers, then f (x) is onto.

Bijective functions A function f : X Y is Bijective f is one-to-one and onto n Examples: 1. A linear function f (x) = ax + b is a Bijective function from the set of real numbers to itself p 2. The function f (x) = x 3 is Bijective from the set of real numbers to itself. p

Inverse function Given a function y = f (x), the inverse f -1 is the set {(y, x) | y = f (x)}. p The inverse f -1 of f is not necessarily a function. p n p Example: if f (x) = x 2, then f -1 (4) = 4 = ± 2, not a unique value and therefore f is not a function. However, if f is a Bijective function, it can be shown that f -1 is a function.

Composition of functions p Given two functions g : X Y and f : Y Z, the composition f ◦ g is defined as follows: f ◦ g (x) = f( g (x)) for every x X. q Example: g (x) = x 2 -1, f (x) = 3 x + 5. Then f ◦ g (x) = f (g (x)) = f(3 x + 5) = (3 x + 5)2 - 1 Composition of functions is associative: f ◦ (g ◦h) = (f ◦ g) ◦ h, q But, in general, it is not commutative: f ◦ g g ◦ f. q