Discrete Mathematics Math Review Math Review Exponents logarithms

Discrete Mathematics Math Review

Math Review: Exponents, logarithms, polynomials, limits, floors and ceilings* * This background review is useful for learning how to analyze the time complexity of computer algorithms.

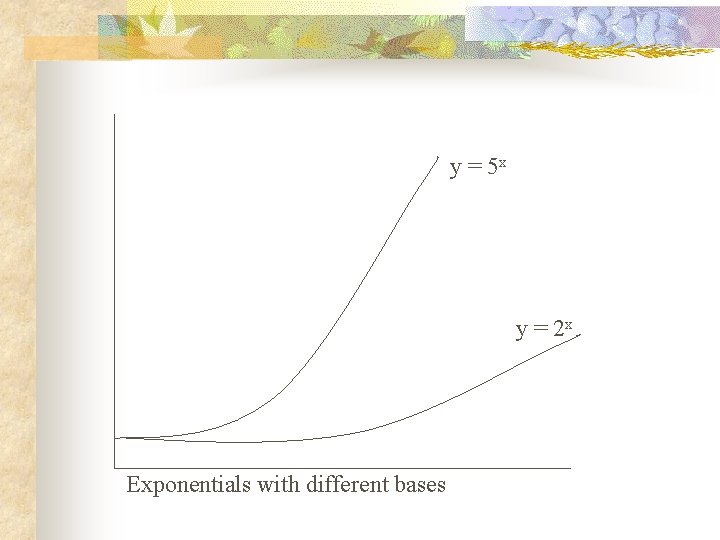
Exponents n Let n be a positive integer, and b be a fixed positive real number. Then the function (n times) fb(n) = bn = b * b … * b is an exponential function. The base is b.

y = 5 x y = 2 x Exponentials with different bases

Rules for exponents (a, b, x, and y assumed to be real numbers) bxby = bx+y (not bxy !!) b 0 = 1 bx / by = bx-y (bx )y = bxy bx + bx = 2 bx For example, 2 x + 2 x = 2 x+1 If bx = by then x = y.

Rules for exponents, continued (a, b, x, and y assumed to be real numbers) (ab)x = axbx (a/b)x = ax/bx If b is not equal to 0, then b–x = 1 / bx x 1/x If x is a positive integer, then b = b For example, 91/2 = 9 = 3

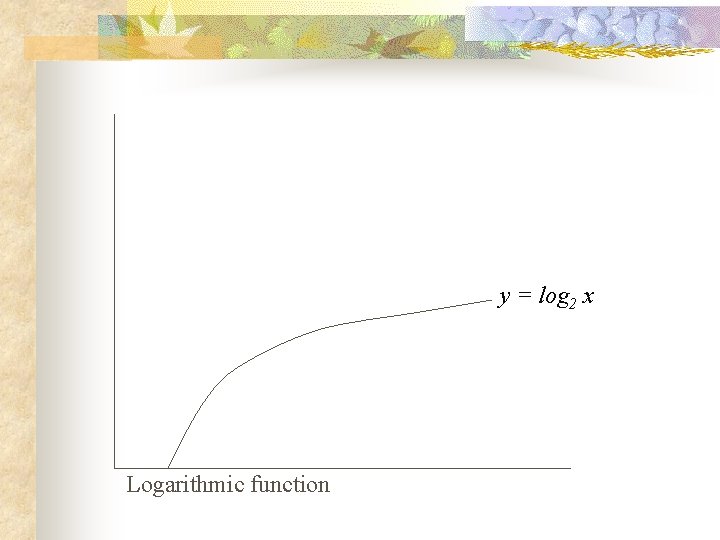
Logarithms n n Suppose b is a real number, with b >1, and x is positive. Then fb(x) = bx is a strictly increasing function of x, and it is a 1 -1 correspondence. Therefore it has an inverse, called the logarithmic function to the base b (logbx). This means: blog bx = x This is the logarithm of x to the base b. Therefore we can conclude that logbbx = x.

Logarithms n Definition: bx = y if and only if logby = x n Example: 102 = 100 means log 10100 = 2

Rules for logarithms (b a real number greater than 1, and x and y positive real numbers) logb(xy) = logbx + logby logb(x/y) = logbx – logby logb (x y)= y logbx

y = log 2 x Logarithmic function

Relationship between logarithms with different bases n Theorem: logax = logbx / logba Proof: Let X = logbx, Y = logba, and Z = logax. By the definition of logarithm: b. X = x, b. Y = a, and a. Z = x. Thus b. X = x = a. Z = (b. Y)Z = b. YZ and therefore X = YZ and therefore we conclude Z = X/Y.

Note on textbooks n When the textbooks refer to log x without specifying a base, the base is assumed to be 2.

Factorial n! = n (n-1)(n-2)(n-3)… 1 n Example: 5! = 5*4*3*2*1

Polynomials n n A polynomial is an expression of the form: anx n + an-1 xn-1 +… + a 2 x 2 + a 1 x + a 0 The ai are real numbers called coefficients, and variable x is called an indeterminate. The largest exponent of the indeterminate in the polynomial determines its order. The order of the polynomial above is xn. A polynomial is typically written in decreasing size of exponents. Examples: n n 3 x 4 + 6 x 2 + x + 9 23 x 7 + 4 x 3 + 2

Rules for polynomials Rule for addition of two polynomials: (anxn + … + a 2 x 2 + a 1 x + a 0) + (bnxn + … + b 2 x 2 + b 1 x + b 0) = (an+bn)xn + … + (a 2+b 2)x 2 + (a 1+b 1)x + (a 0+b 0) Rule for multiplication of two polynomials: (anxn + … + a 2 x 2 + a 1 x + a 0) * (bmxm + … + b 2 x 2 + b 1 x + b 0) = (anbm)xn+m + … + (a 0 b 2+ a 1 b 1 + a 2 b 0)x 2 + (a 0 b 1 + a 1 b 0)x + (a 0 b 0) n n In general, for each k >= 0, the coefficient of xk in the product is: k i=0 ai bk-i , where ai = 0 if i > n and bj = 0 if j > m.

Intervals n n n An open interval (a, b) consists of all real numbers between two fixed numbers a and b: I = {x | a < x < b} A closed interval [a, b] contains both endpoints: I = {x | a <= x <= b} A half-open interval (a, b] or [a, b) contains one endpoint: I = {x | a < x <= b} or I = {x | a <= x < b}

Neighborhoods n n n The set of numbers that are close to a fixed number c is a neighborhood of c. This implies that |x – c| is small. A deleted neighborhood of c excludes c. In this case, |x – c| > 0. A symmetric neighborhood of c can be described by |x – c| < h for some small positive number h. A deleted symmetric neighborhood of c is described by 0 < |x – c| < h. An open interval containing c is a neighborhood of c. For example the open interval (c – h, c + h) is a symmetric neighborhood of c.

Limits n Definition: Suppose f is a function defined for values of x near a. The domain of f need not include a, though it may. We say that: L is the limit of f(x) as x approaches a, and write: L = lim f(x) x a provided that, for every real number h > 0 there is a deleted neighborhood N of a such that: L – h < f(x) < L + h whenever x is in N and in the domain of f.

Limits n n Alternative definition: L is the limit of f(x) as x approaches a, and write: L = lim f(x) x a provided that, for every real number h > 0 there exists a real number d > 0 such that: |f(x) – L| < h whenever 0 < |x – a| < d. Translated to predicate logic: h d x ((0 < |x – a| < d) (|f(x) – L| < h)) when the universe of discourse for h and d is the set of positive real numbers and for x is the set of real numbers.

Floors and Ceilings For all real x and integer n: x = the greatest integer less than or equal to x x = the least integer less than or equal to x n = n x = n n x n+1 x = n x-1 n x x = n n x n+1 x = n x+1 x + n = x + n n/2 + n/2 = n x = x Examples: 3. 9 = 4 3. 9 = 3 = 3. 9 = 4 = 3. 9