Discrete Mathematics Lecture 8 Dr Ing Erwin Sitompul

Discrete Mathematics Lecture 8 Dr. -Ing. Erwin Sitompul President University http: //zitompul. wordpress. com 2 President University 0 1 6 Erwin Sitompul Discrete Mathematics 8/1

Chapter 5 Permutation and Combination Homework 7 1. A chairperson and a treasurer of PUMA IE should be chosen out of 50 eligible association members. In how many ways can a chairperson and a treasurer can be elected, if: a. There is no limitation. b. Angga wants to serve only if elected as a chairperson. c. Benny and Cora want to be elected together or not at all. d. David and Edmond do not want to work together. • The position of chairperson and treasurer are different. • The sequence of election must be considered. • The problem in this homework is a permutation problem. President University Erwin Sitompul Discrete Mathematics 8/2

Chapter 5 Permutation and Combination Solution to Homework 7 a. There is no limitation. b. Amir wants to serve only if elected as a chairperson. Angga is not elected as chairperson an thus does not want to serve; the 2 positions will now be filled by the remaining 49 members Angga is elected as chairperson, with 49 ways to fill the treasurer position President University Erwin Sitompul Discrete Mathematics 8/3

Chapter 5 Permutation and Combination Solution to Homework 7 c. Benny and Cora want to be elected together or not at all. The wish of Benny and Cora does not come true; and from the remaining 48 members, 2 people will be elected to fill the positions Benny and Cora are elected together President University Erwin Sitompul Discrete Mathematics 8/4

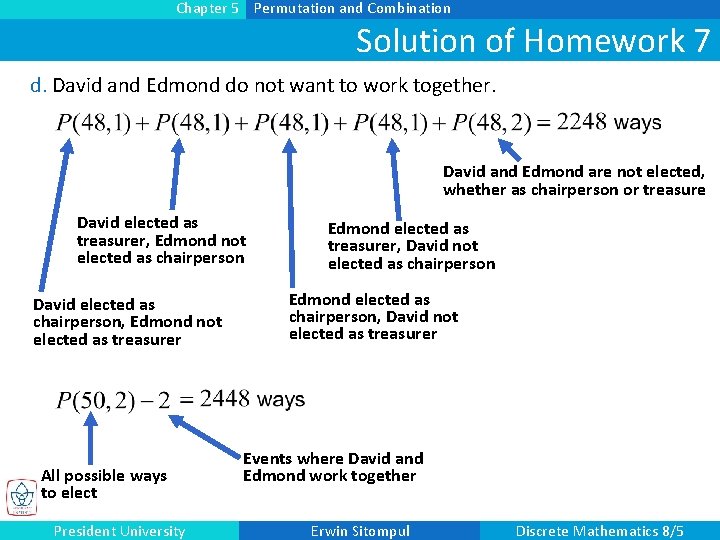
Chapter 5 Permutation and Combination Solution of Homework 7 d. David and Edmond do not want to work together. David and Edmond are not elected, whether as chairperson or treasure David elected as treasurer, Edmond not elected as chairperson David elected as chairperson, Edmond not elected as treasurer All possible ways to elect President University Edmond elected as treasurer, David not elected as chairperson Edmond elected as chairperson, David not elected as treasurer Events where David and Edmond work together Erwin Sitompul Discrete Mathematics 8/5

Discrete Mathematics Chapter 6 Graphs President University Erwin Sitompul Discrete Mathematics 8/6

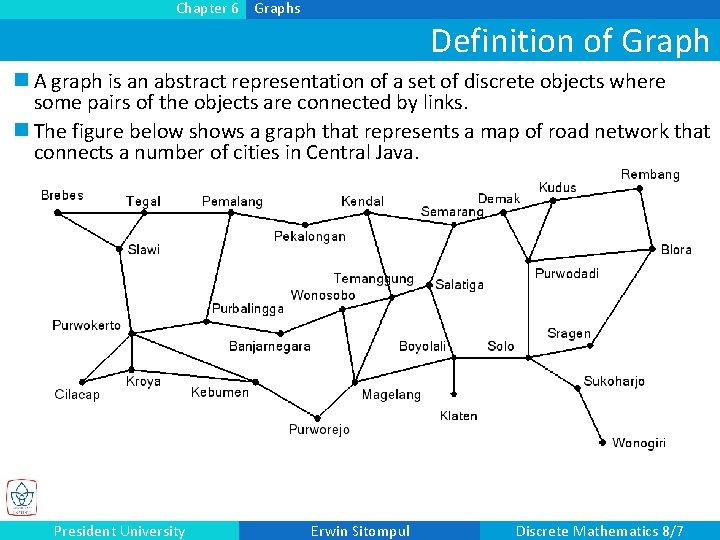
Chapter 6 Graphs Definition of Graph n A graph is an abstract representation of a set of discrete objects where some pairs of the objects are connected by links. n The figure below shows a graph that represents a map of road network that connects a number of cities in Central Java. President University Erwin Sitompul Discrete Mathematics 8/7

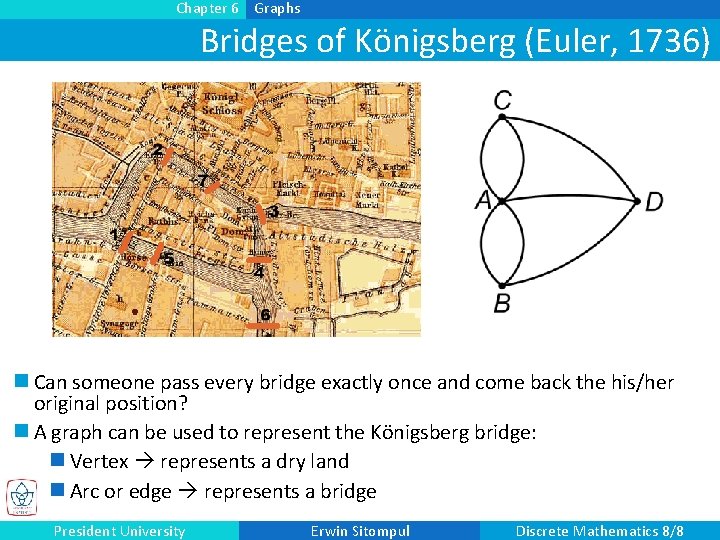
Chapter 6 Graphs Bridges of Königsberg (Euler, 1736) n Can someone pass every bridge exactly once and come back the his/her original position? n A graph can be used to represent the Königsberg bridge: n Vertex represents a dry land n Arc or edge represents a bridge President University Erwin Sitompul Discrete Mathematics 8/8

Chapter 6 Graphs Graph Representation n Graph is denoted as G = (V, E), where: n V = set of vertices, may not be a null set = {v 1, v 2, . . . , vn} n E = Set of edges, each connecting a pair of vertices = {e 1, e 2, . . . , en} n Graph G 1 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (1, 3), (2, 4), (3, 4)} G 1 Simple graph President University Erwin Sitompul Discrete Mathematics 8/9

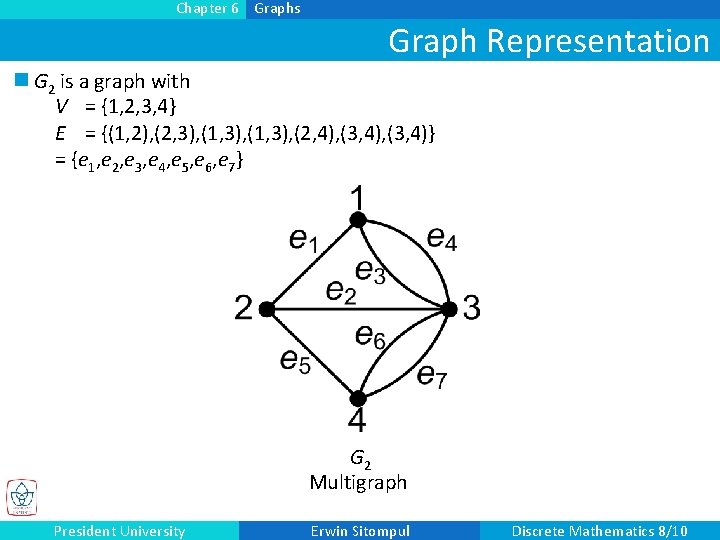
Chapter 6 Graphs Graph Representation n G 2 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (2, 3), (1, 3), (2, 4), (3, 4)} = {e 1, e 2, e 3, e 4, e 5, e 6, e 7} G 2 Multigraph President University Erwin Sitompul Discrete Mathematics 8/10

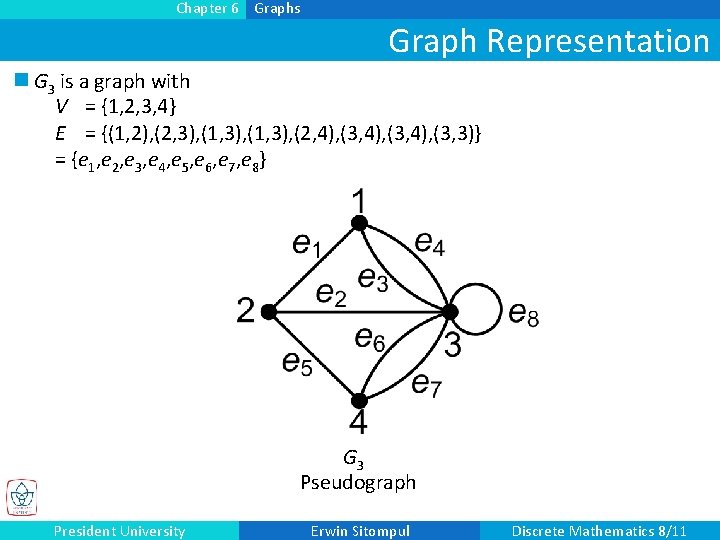
Chapter 6 Graphs Graph Representation n G 3 is a graph with V = {1, 2, 3, 4} E = {(1, 2), (2, 3), (1, 3), (2, 4), (3, 3)} = {e 1, e 2, e 3, e 4, e 5, e 6, e 7, e 8} G 3 Pseudograph President University Erwin Sitompul Discrete Mathematics 8/11

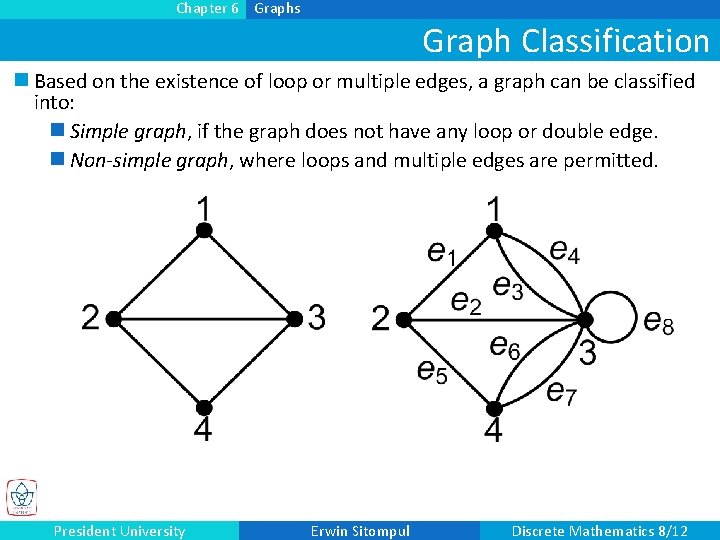
Chapter 6 Graphs Graph Classification n Based on the existence of loop or multiple edges, a graph can be classified into: n Simple graph, if the graph does not have any loop or double edge. n Non-simple graph, where loops and multiple edges are permitted. President University Erwin Sitompul Discrete Mathematics 8/12

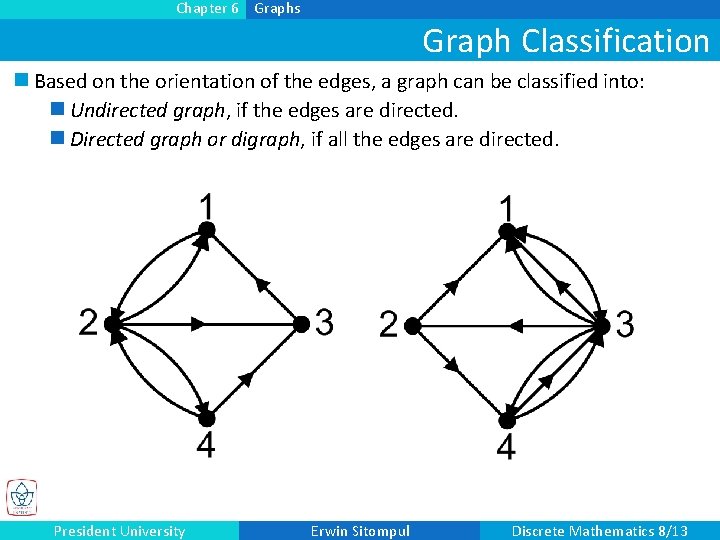
Chapter 6 Graphs Graph Classification n Based on the orientation of the edges, a graph can be classified into: n Undirected graph, if the edges are directed. n Directed graph or digraph, if all the edges are directed. President University Erwin Sitompul Discrete Mathematics 8/13

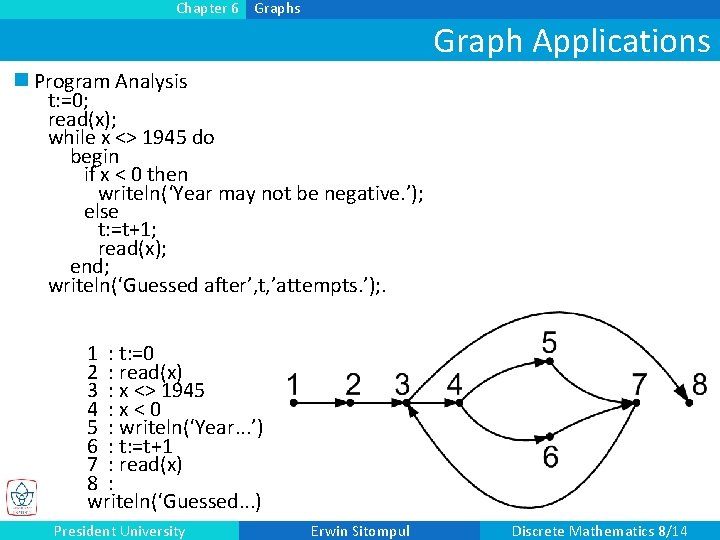
Chapter 6 Graphs Graph Applications n Program Analysis t: =0; read(x); while x <> 1945 do begin if x < 0 then writeln(‘Year may not be negative. ’); else t: =t+1; read(x); end; writeln(‘Guessed after’, t, ’attempts. ’); . 1 : t: =0 2 : read(x) 3 : x <> 1945 4 : x<0 5 : writeln(‘Year. . . ’) 6 : t: =t+1 7 : read(x) 8 : writeln(‘Guessed. . . ) President University Erwin Sitompul Discrete Mathematics 8/14

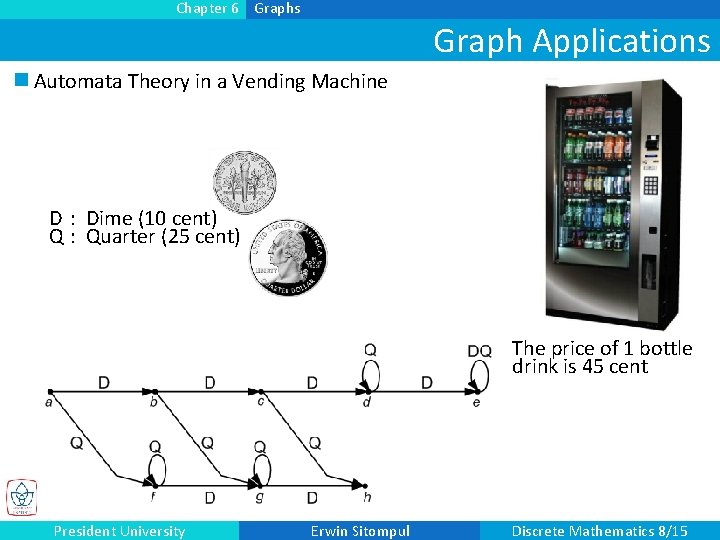
Chapter 6 Graphs Graph Applications n Automata Theory in a Vending Machine D : Dime (10 cent) Q : Quarter (25 cent) The price of 1 bottle drink is 45 cent President University Erwin Sitompul Discrete Mathematics 8/15

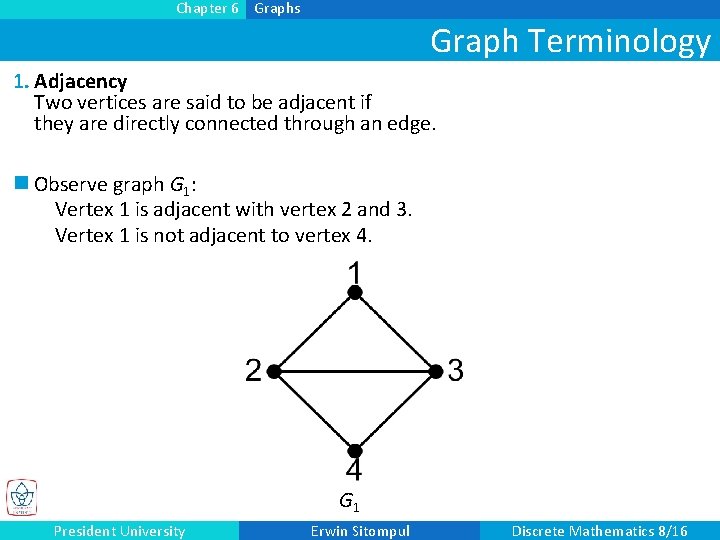
Chapter 6 Graphs Graph Terminology 1. Adjacency Two vertices are said to be adjacent if they are directly connected through an edge. n Observe graph G 1: Vertex 1 is adjacent with vertex 2 and 3. Vertex 1 is not adjacent to vertex 4. G 1 President University Erwin Sitompul Discrete Mathematics 8/16

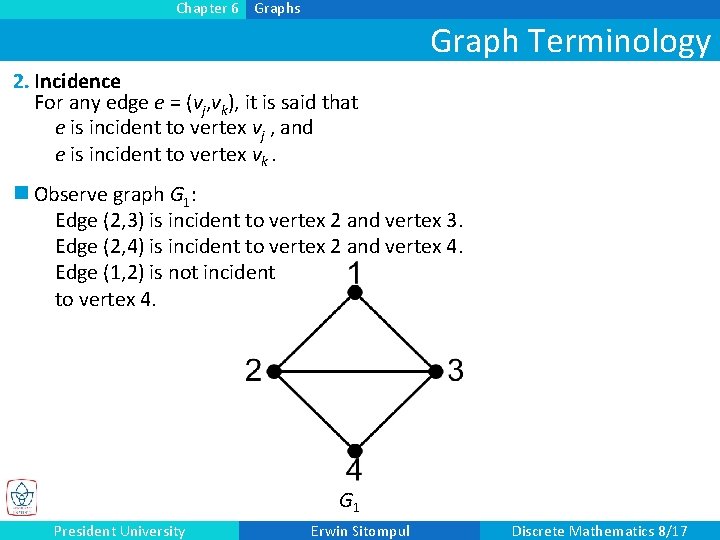
Chapter 6 Graphs Graph Terminology 2. Incidence For any edge e = (vj, vk), it is said that e is incident to vertex vj , and e is incident to vertex vk. n Observe graph G 1: Edge (2, 3) is incident to vertex 2 and vertex 3. Edge (2, 4) is incident to vertex 2 and vertex 4. Edge (1, 2) is not incident to vertex 4. G 1 President University Erwin Sitompul Discrete Mathematics 8/17

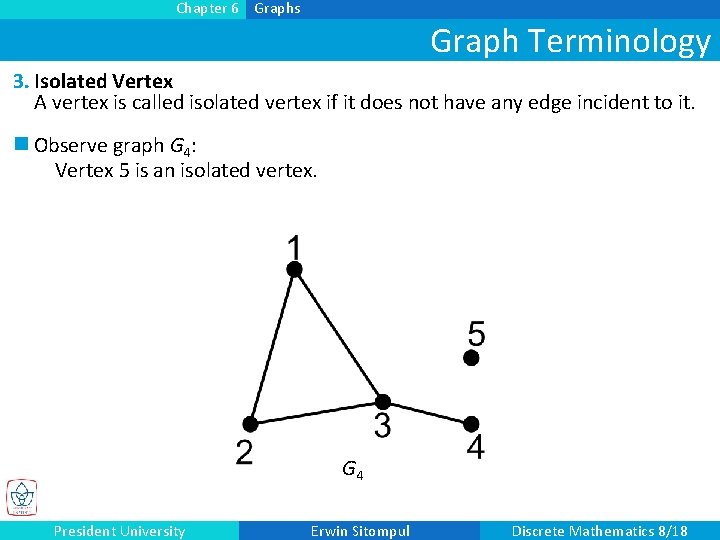
Chapter 6 Graphs Graph Terminology 3. Isolated Vertex A vertex is called isolated vertex if it does not have any edge incident to it. n Observe graph G 4: Vertex 5 is an isolated vertex. G 4 President University Erwin Sitompul Discrete Mathematics 8/18

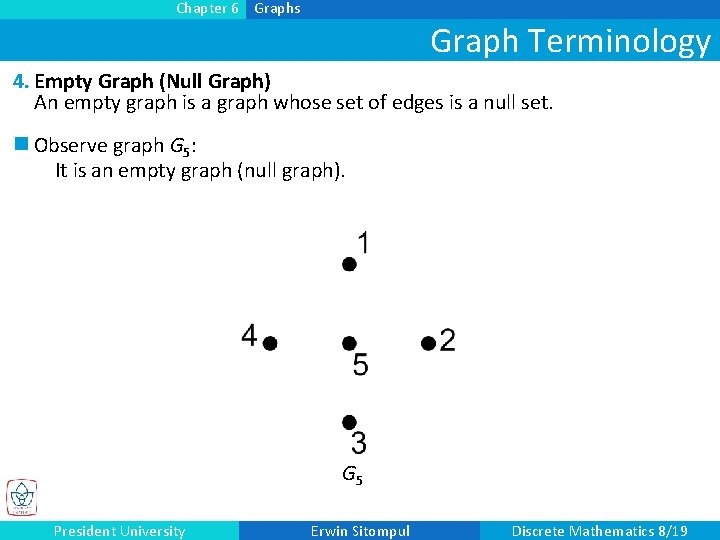
Chapter 6 Graphs Graph Terminology 4. Empty Graph (Null Graph) An empty graph is a graph whose set of edges is a null set. n Observe graph G 5: It is an empty graph (null graph). G 5 President University Erwin Sitompul Discrete Mathematics 8/19

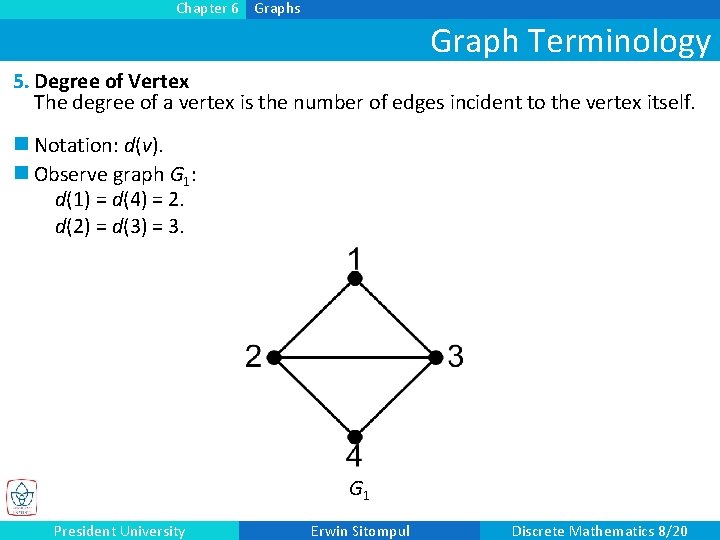
Chapter 6 Graphs Graph Terminology 5. Degree of Vertex The degree of a vertex is the number of edges incident to the vertex itself. n Notation: d(v). n Observe graph G 1: d(1) = d(4) = 2. d(2) = d(3) = 3. G 1 President University Erwin Sitompul Discrete Mathematics 8/20

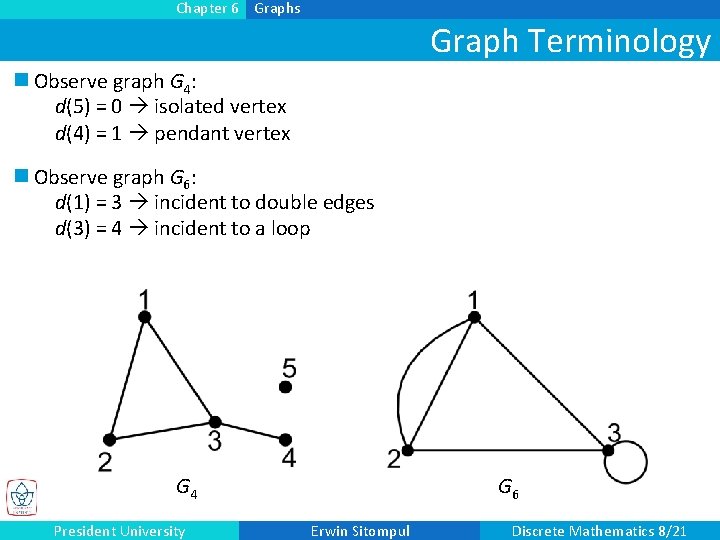
Chapter 6 Graphs Graph Terminology n Observe graph G 4: d(5) = 0 isolated vertex d(4) = 1 pendant vertex n Observe graph G 6: d(1) = 3 incident to double edges d(3) = 4 incident to a loop G 4 President University G 6 Erwin Sitompul Discrete Mathematics 8/21

Chapter 6 Graphs Graph Terminology n In a directed graph (digraph): din(v) = in-degree = number of arcs arriving to a vertex dout(v) = out-degree = number of arcs departing from a vertex d(v) = din(v) + dout(v) n Observe graph G 7: din(1) = 2 dout(1) = 1 din(2) = 2 dout(2) = 3 din(3) = 2 dout(3) = 1 din(4) = 1 dout(4) = 2 G 7 President University Erwin Sitompul Discrete Mathematics 8/22

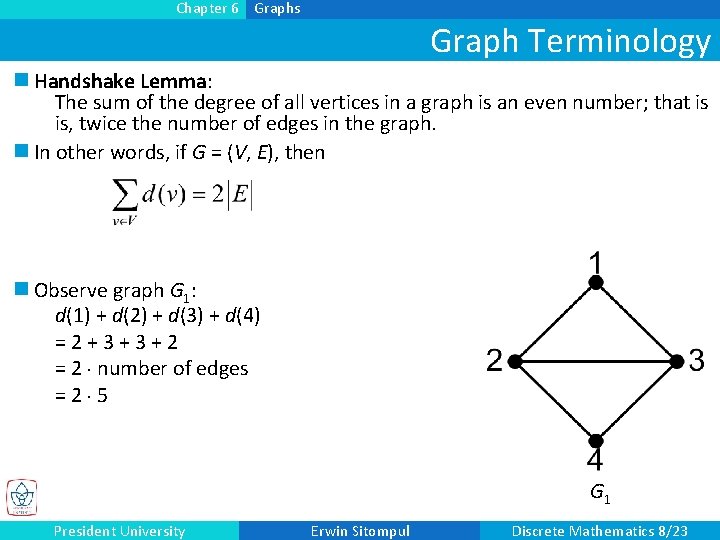
Chapter 6 Graphs Graph Terminology n Handshake Lemma: The sum of the degree of all vertices in a graph is an even number; that is is, twice the number of edges in the graph. n In other words, if G = (V, E), then n Observe graph G 1: d(1) + d(2) + d(3) + d(4) =2+3+3+2 = 2 number of edges =2 5 G 1 President University Erwin Sitompul Discrete Mathematics 8/23

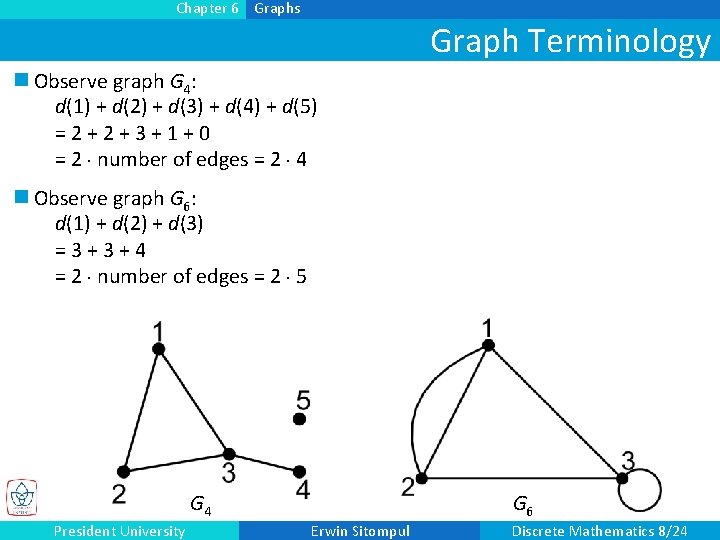
Chapter 6 Graphs Graph Terminology n Observe graph G 4: d(1) + d(2) + d(3) + d(4) + d(5) =2+2+3+1+0 = 2 number of edges = 2 4 n Observe graph G 6: d(1) + d(2) + d(3) =3+3+4 = 2 number of edges = 2 5 G 4 President University G 6 Erwin Sitompul Discrete Mathematics 8/24

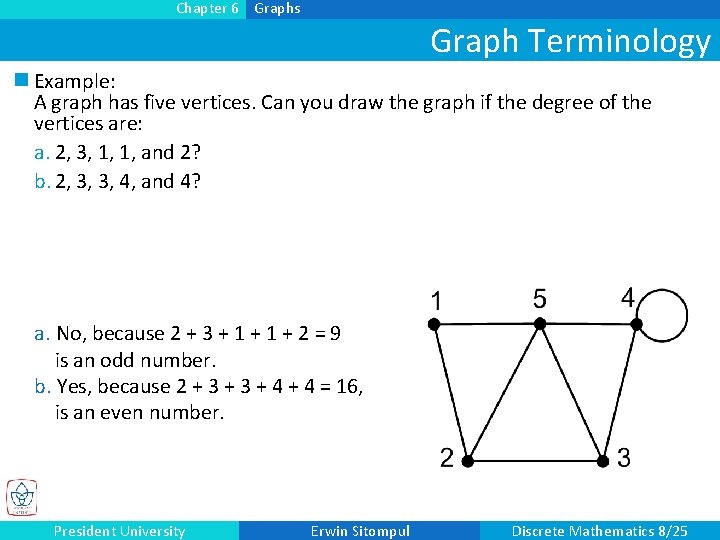
Chapter 6 Graphs Graph Terminology n Example: A graph has five vertices. Can you draw the graph if the degree of the vertices are: a. 2, 3, 1, 1, and 2? b. 2, 3, 3, 4, and 4? a. No, because 2 + 3 + 1 + 2 = 9 is an odd number. b. Yes, because 2 + 3 + 4 = 16, is an even number. President University Erwin Sitompul Discrete Mathematics 8/25

Chapter 6 Graphs Graph Terminology 6. Path A path with length n from vertex of origin v 0 to vertex of destination vn in a graph G is the alternating sequence of vertices and edges in the form of v 0, e 1, v 1, e 2, v 2, . . . , vn – 1, en, vn such that e 1 = (v 0, v 1), e 2 = (v 1, v 2), . . . , en = (vn– 1, vn) are the edges of graph G. n The length of a path is determined by the number of edges in that path. n Observe graph G 1: Path 1, 2, 4, 3 is a path with edge sequence of (1, 2), (2, 4), and (4, 3). The length of path 1, 2, 4, 3 is 3. G 1 President University Erwin Sitompul Discrete Mathematics 8/26

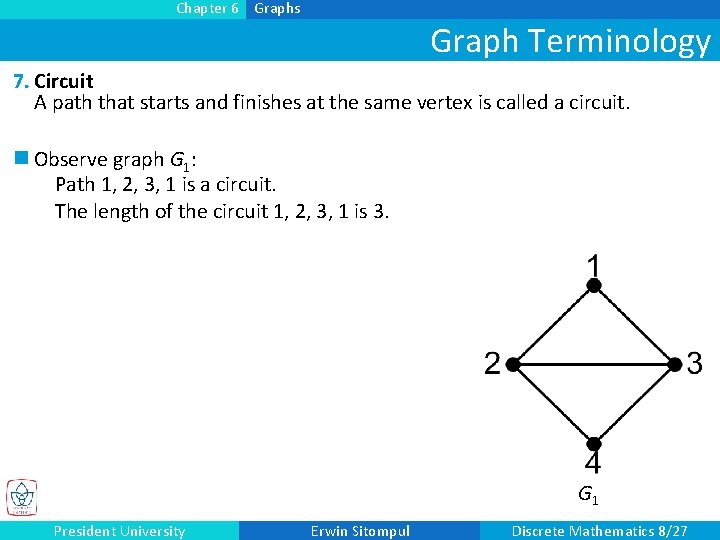
Chapter 6 Graphs Graph Terminology 7. Circuit A path that starts and finishes at the same vertex is called a circuit. n Observe graph G 1: Path 1, 2, 3, 1 is a circuit. The length of the circuit 1, 2, 3, 1 is 3. G 1 President University Erwin Sitompul Discrete Mathematics 8/27

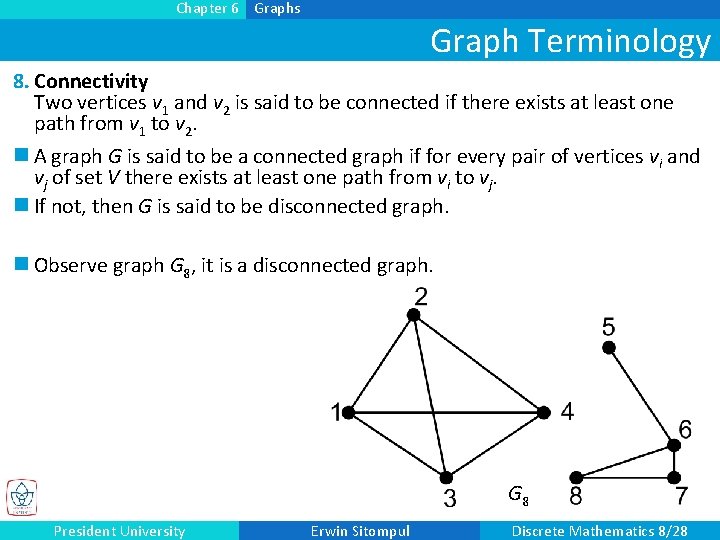
Chapter 6 Graphs Graph Terminology 8. Connectivity Two vertices v 1 and v 2 is said to be connected if there exists at least one path from v 1 to v 2. n A graph G is said to be a connected graph if for every pair of vertices vi and vj of set V there exists at least one path from vi to vj. n If not, then G is said to be disconnected graph. n Observe graph G 8, it is a disconnected graph. G 8 President University Erwin Sitompul Discrete Mathematics 8/28

Chapter 6 Graphs Graph Terminology n A directed graph G is said to be connected if its non-directed graph is connected. n Note: The non-directed graph of a directed graph G is obtained by omitting all arrow heads). n Two vertices, u and v, in a directed graph G are said as strongly connected vertices if there exists a directed path from u to v and also from v to u. n If u and v are not strongly connected vertices but the non-directed graph of G is a connected one, then u and v are said as weakly connected vertices. President University Erwin Sitompul Discrete Mathematics 8/29

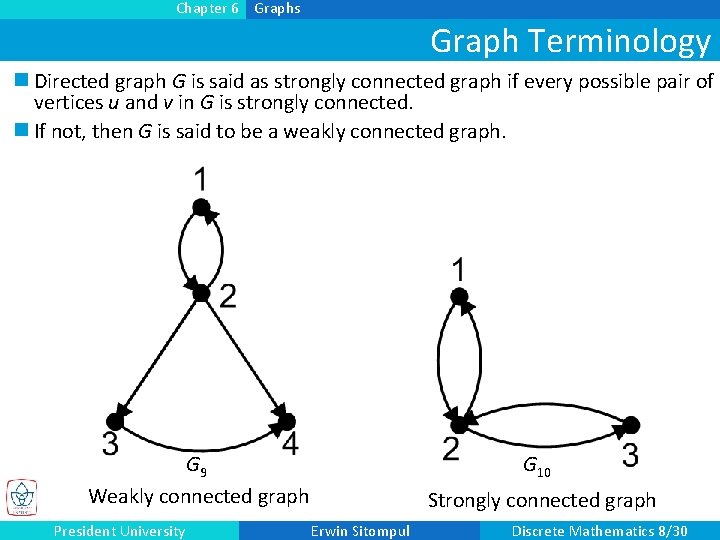
Chapter 6 Graphs Graph Terminology n Directed graph G is said as strongly connected graph if every possible pair of vertices u and v in G is strongly connected. n If not, then G is said to be a weakly connected graph. G 9 Weakly connected graph President University G 10 Strongly connected graph Erwin Sitompul Discrete Mathematics 8/30

Chapter 6 Graphs Graph Terminology 9. Subgraph and Subgraph Complement n Suppose G = (V, E) is a graph, then G 1 = (V 1, E 1) is a subgraph of G if V 1 V and E 1 E. n Complement of subgraph G 1 in regard to graph G is the graph G 2 = (V 2, E 2) such that E 2 = E – E 1 and V 2 is the set of all vertices incident to all members of E 2. G 11 President University A subgraph of G 11 Erwin Sitompul Complement of the subgraph of G 11 Discrete Mathematics 8/31

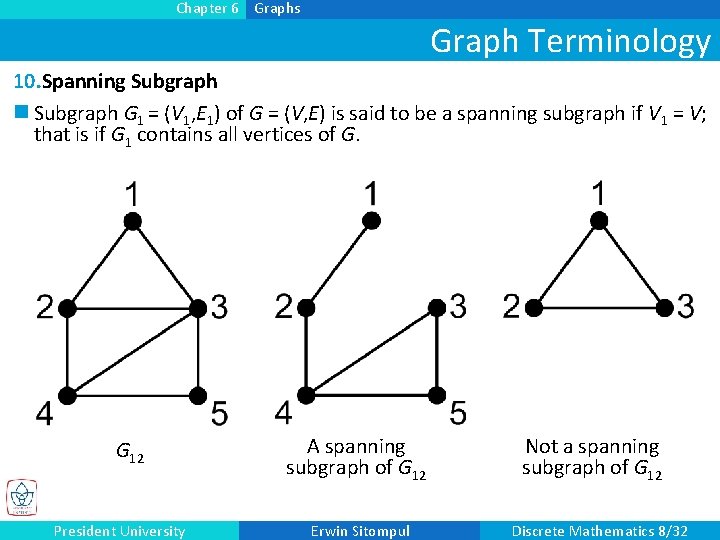
Chapter 6 Graphs Graph Terminology 10. Spanning Subgraph n Subgraph G 1 = (V 1, E 1) of G = (V, E) is said to be a spanning subgraph if V 1 = V; that is if G 1 contains all vertices of G. G 12 President University A spanning subgraph of G 12 Erwin Sitompul Not a spanning subgraph of G 12 Discrete Mathematics 8/32

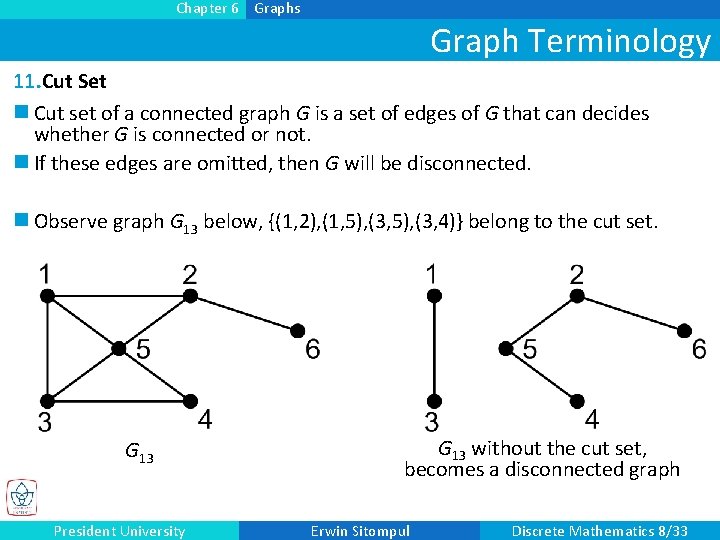
Chapter 6 Graphs Graph Terminology 11. Cut Set n Cut set of a connected graph G is a set of edges of G that can decides whether G is connected or not. n If these edges are omitted, then G will be disconnected. n Observe graph G 13 below, {(1, 2), (1, 5), (3, 4)} belong to the cut set. G 13 President University G 13 without the cut set, becomes a disconnected graph Erwin Sitompul Discrete Mathematics 8/33

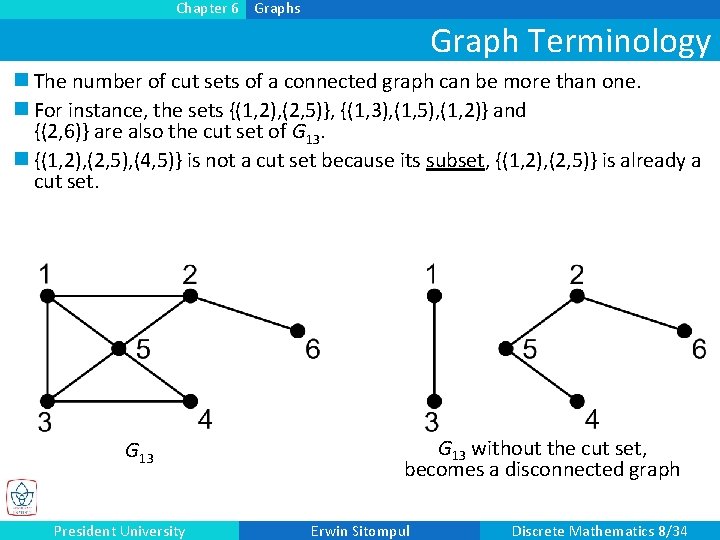
Chapter 6 Graphs Graph Terminology n The number of cut sets of a connected graph can be more than one. n For instance, the sets {(1, 2), (2, 5)}, {(1, 3), (1, 5), (1, 2)} and {(2, 6)} are also the cut set of G 13. n {(1, 2), (2, 5), (4, 5)} is not a cut set because its subset, {(1, 2), (2, 5)} is already a cut set. G 13 President University G 13 without the cut set, becomes a disconnected graph Erwin Sitompul Discrete Mathematics 8/34

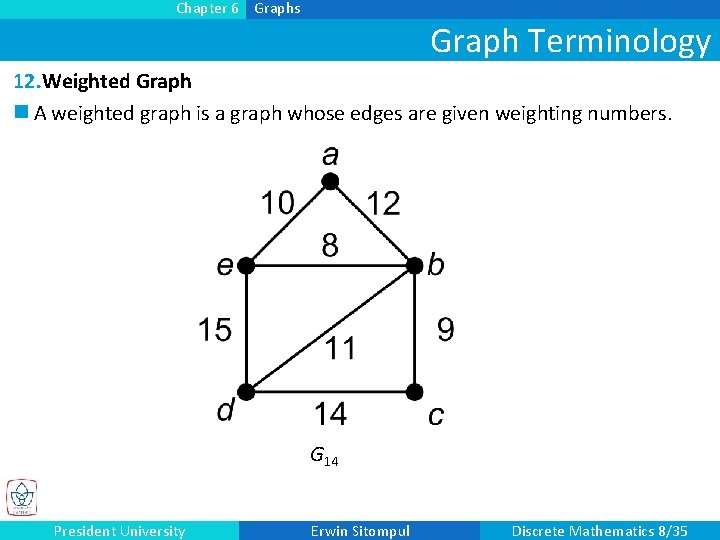
Chapter 6 Graphs Graph Terminology 12. Weighted Graph n A weighted graph is a graph whose edges are given weighting numbers. G 14 President University Erwin Sitompul Discrete Mathematics 8/35

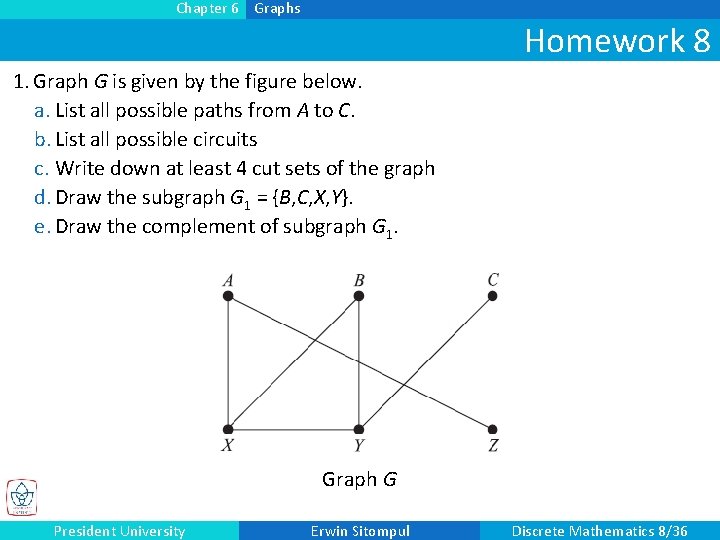
Chapter 6 Graphs Homework 8 1. Graph G is given by the figure below. a. List all possible paths from A to C. b. List all possible circuits c. Write down at least 4 cut sets of the graph d. Draw the subgraph G 1 = {B, C, X, Y}. e. Draw the complement of subgraph G 1. Graph G President University Erwin Sitompul Discrete Mathematics 8/36

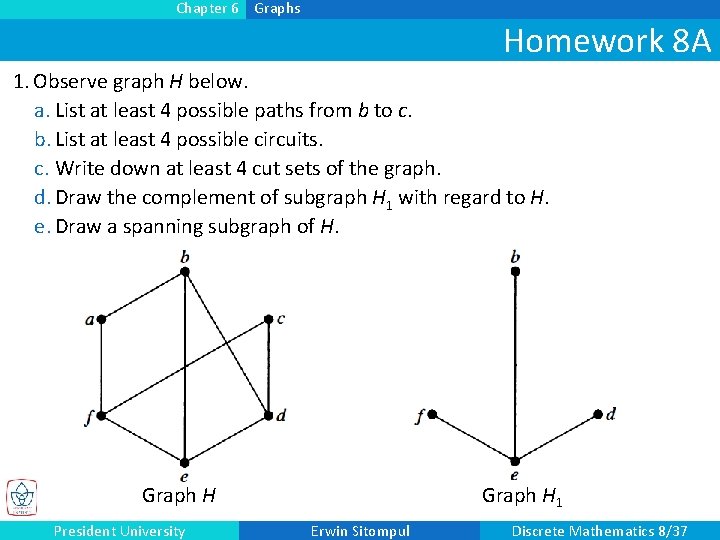
Chapter 6 Graphs Homework 8 A 1. Observe graph H below. a. List at least 4 possible paths from b to c. b. List at least 4 possible circuits. c. Write down at least 4 cut sets of the graph. d. Draw the complement of subgraph H 1 with regard to H. e. Draw a spanning subgraph of H. Graph H President University Graph H 1 Erwin Sitompul Discrete Mathematics 8/37