Discrete Mathematics Lecture 1 Dr Ing Erwin Sitompul

Discrete Mathematics Lecture 1 Dr. -Ing. Erwin Sitompul President University http: //zitompul. wordpress. com 2 President University 0 1 6 Erwin Sitompul Discrete Mathematics 1/1

Discrete Mathematics Text Book and Syllabus n Text book: Kenneth H. Rosen, “Discrete Mathematics and Its Applications”, 6 th Edition, Mc. Graw-Hill International Edition, 2007. n Tentative Syllabus: 1. Logic and Proofs 2. Sets 3. Relation and Functions 4. Sequences and Summations 5. Number Theory 6. Counting and Combinatorial 7. Graphs President University Erwin Sitompul Discrete Mathematics 1/2

Discrete Mathematics Grade Policy Final Grade = 5% Notes + 9% Homework + 19% Quizzes + 29% Midterm Exam + 39% Final Exam + Extra Points n Notes must be handwritten, and will be graded based on the completeness and clarity. n The handwritten note will be checked on Lecture 11 (after Quiz 3), and given back to you on Lecture 12. It contributes 5% of final grade. n Homeworks will be given in fairly regular basis. The average of homework grades contributes 9% of final grade. n Written homeworks are to be submitted on A 4 papers, otherwise they will not be graded. n Homeworks must be submitted on time, one day before the next lecture. Late submission will be penalized by point deduction of – 10·n, where n is the total number of lateness made. n There will be 3 quizzes. Only the best 2 will be counted. The average of quiz grades contributes 19% of final grade. President University Erwin Sitompul Discrete Mathematics 1/3

Discrete Mathematics Grade Policy n Midterm and final exams follow the schedule released by AAB (Academic Administration Bureau). n Make up of quizzes must be requested within one week after the schedule of the respective quiz. n Make up for mid exam and final exam must be requested directly to AAB. Thermal Physics Homework 2 Emelie Raturandang 002202400058 21 March 2027 No. 1. Answer: . . . . ● Heading of Written Homework Papers (Required) President University Erwin Sitompul Discrete Mathematics 1/4

Discrete Mathematics Grade Policy n Extra points will be given if you solve a problem in front of the class. You will earn 1 or 2. n Lecture slides can be copied during class session. It is also available on internet. Please check the course homepage regularly. http: //zitompul. wordpress. com n The use of internet for any purpose during class sessions is strictly forbidden. President University Erwin Sitompul Discrete Mathematics 1/5

Discrete Mathematics Chapter 0 Introduction President University Erwin Sitompul Discrete Mathematics 1/6

Chapter 0 Introduction What is “Discrete Mathematics”? n Discrete Mathematics is a branch of mathematics that discuss about discrete objects or structures. Discrete objects or structures can assume only distinct, separated values. n The term “discrete mathematics” is therefore used in contrast with “continuous mathematics” which is the branch of mathematics dealing with objects that can vary smoothly (for example, calculus). n What is the definition of discrete? n An object can be said to be discrete if : n It consists of unconnected distinct parts / members n It consists of finite or countable parts / members President University Erwin Sitompul Discrete Mathematics 1/7

Chapter 0 Introduction What is “Discrete Mathematics”? n Example of discrete objects: n Integers: between two integers there is no other integer. n Propositions: either true or false, there are no half true or half false. n Sets: an object is whether in a set or not in a set, it never partly in and partly out. n Relations: a pair of objects are whether related or not at all. n Graphs: In a network, between two terminals of a direct connection, there are no other terminals. President University Erwin Sitompul Discrete Mathematics 1/8

Chapter 0 Introduction Discrete Mathematics in Electrical Engineering n Discrete Mathematics is relevant to Electrical Engineering, because we often deal with objects with discrete properties. n Consider a digital signal processing of a video clip: n The color is discretized into 3 hues: Red, Green, and Blue. n The hue is discretized into discrete intensity level, 0 -255. n The pixels are discrete objects in space. n The frames are discrete objects in time. n In the digital world nowadays, often discrete variables are used to represent a phenomena in discretely rather than continuously. n The states of a computer program are discrete. n The states of a digital hardware design are discrete. n Discrete structures (sets, functions, relations, trees, graphs) are very useful for representing data in computers. n Connecting a generator or a load to a power grid is a discrete change. n The measurement result of a sensor is discretized before it is processed. President University Erwin Sitompul Discrete Mathematics 1/9

Chapter 0 Introduction What is “Discrete Mathematics”? n Some examples of problems related with Discrete Mathematics: n How many different password can be made out of 8 different characters? n How does a credit card number is validated? n How many 8 -bit-long binary string combinations can be made if the sum of bit-1 must be odd? n How to determine the shortest path between point A and point B in a factory complex? n Proof that a combination of 3 s and 5 s can result any integer number higher than 8. n How many different FM frequencies are needed to be assigned to commercial radio stations so that the stations do not interfere each other? President University Erwin Sitompul Discrete Mathematics 1/10

Chapter 0 Introduction What is “Discrete Mathematics”? n Some examples of problems related with Discrete Mathematics: n How to construct logic circuit for a seven segments? n Can you walk through all the streets in your housing complex exactly once and come back to the original position? n “Cheap food is not tasty. ” “Tasty food is not cheap. ” Are both statements telling us the same thing? President University Erwin Sitompul Discrete Mathematics 1/11

Discrete Mathematics Chapter 1 Logic and Proofs President University Erwin Sitompul Discrete Mathematics 1/12

Chapter 1 Logic and Proofs Logic and Proposition n Logic defines a formal language for representing knowledge and for making logical inferences. n Logic helps us to understand how to construct a valid argument. n Logic defines: n Syntax of statements / propositions n The meaning of statements / propositions n The rules of logical inference n Logic is the basic of reasoning, which is based on relations between statements / propositions. President University Erwin Sitompul Discrete Mathematics 1/13

Chapter 1 Logic and Proofs Proposition n A proposition is a statement that can be either true or false, but not both. n Some examples of proposition: n “ 13 is an odd number. ” n “Ir. Soekarno was graduated from UGM. ” n “It is raining today. ” n “The day after tomorrow is Wednesday. ” n “There are other life forms on other planets in the universe. ” n “For any integer n 0, there exists 2 n which is an even number. ” n “x + y = y + x for any real number x and y. ” n “ 1 + 1 = 2. ” n “x – 5 = 8, where x = 14. ” President University Erwin Sitompul Discrete Mathematics 1/14

Chapter 1 Logic and Proofs Proposition n These statements are not proposition: n “How old are you? ” ·A question is not a proposition n “Do the quiz without cooperating!” ·A command is not a proposition n “x + 5 = 3. ” ·Since x is not specified, neither true or false n “y > 5. ” ·Since y is not specified, neither true or false n “He is tall. ” ·Since ‘he’ is not specified, neither true or false n Conclusion: Propositions are declarative sentences or close sentence. n If a proposition is made out of mathematical equations, then the equations must possess a solution / answer so that its truth value can be determined. President University Erwin Sitompul Discrete Mathematics 1/15

Chapter 1 Logic and Proofs Proposition n Propositions are denoted with lowercase letters, starting with p, such as p, q, r, s, … n Example of proposition: n p : “ 13 is an odd number. ” n q : “Ir. Soekarno was graduated from UGM. ” n r : “ 2 + 2 = 4. ” President University Erwin Sitompul Discrete Mathematics 1/16

Chapter 1 Logic and Proofs Compound Proposition n A compound proposition can be built from elementary propositions by using logical connectives. n Logical connectives are: n Negation n Conjunction n Disjunction n Exclusive or n Conditional (Implication) n Biconditional President University Erwin Sitompul Discrete Mathematics 1/17

Chapter 1 Logic and Proofs Compound Proposition n Given propositions p and q, then: 1. Negation : not p p 2. Conjunction : p and q p q 3. Disjunction : p or q p q ¬p n Combination of more than one proposition result in a compound proposition. President University Erwin Sitompul Discrete Mathematics 1/18

Chapter 1 Logic and Proofs Compound Proposition n Example: The following propositions are given: p : Today is rainy. q : The class is cancelled. The two propositions can be combined to become: p q : “Today is rainy and the class is cancelled. ” p q : “Today is rainy or the class is cancelled. ” p : “It is not true that today is rainy. ” “It is not the case that today is rainy. ” “Today is not rainy. ” President University Erwin Sitompul Discrete Mathematics 1/19

Chapter 1 Logic and Proofs Compound Proposition n Example: Given the following propositions p : “The man is competent. ” q : “The man is assertive. ” Express the following proposition combinations using symbolic notation. p q i. “The man is competent and assertive. ” ii. “The man is competent but not assertive. ” p q iii. “The man is neither competent nor assertive. ” iv. “It is not the case that the man is incompetent ( p q) or not assertive. ” v. “The man is competent, or incompetent and assertive. ” p ( p q) vi. “That the man is incompetent as well as assertive, ( p q) is not true. ” President University Erwin Sitompul Discrete Mathematics 1/20

Chapter 1 Logic and Proofs Truth Table of Compound Proposition n A truth table displays the relationship between the truth values (T or F) of different propositions for a given connective. n The truth table of a compound proposition shows all possible combinations of truth values of elementary propositions. ● Negation ● Conjunction ● Disjunction p p p q p q T F T T F F T F T F F T T F F F President University Erwin Sitompul Discrete Mathematics 1/21

Chapter 1 Logic and Proofs Some Examples n Example: p : “ 17 is a prime number. ” T q : “Prime number is always odd. ” F p q : “ 17 is a prime number and prime number is always odd. ” F n Example: F T “Surabaya was the capital city of Indonesia or tomorrow is Friday. ” T F T n Example: “It is not true that February is the shortest month and energy cannot be created. ” F President University Erwin Sitompul Discrete Mathematics 1/22

Chapter 1 Logic and Proofs Constructing the Truth Table n Example: Build the truth table of the proposition (p q) ( q r). p q r p q q q r (p q) ( q r) T T F F T T F T T F F F F F F F T T T F F President University Erwin Sitompul Discrete Mathematics 1/23

Chapter 1 Logic and Proofs Tautology, Contradiction, and Contingency n A compound proposition which is always true for all cases is called tautology. n A compound proposition which is always false for all cases is called contradiction. n A proposition that is neither a tautology nor contradiction is called a contingency. President University Erwin Sitompul Discrete Mathematics 1/24

Chapter 1 Logic and Proofs Tautology, Contradiction, and Contingency n Example: p (p q) is a tautology. p q (p q) p (p q) T T T F F T T F F F T T n Example: (p q) is a contradiction. p q p q (p q) T T F F F T F F F T F President University Erwin Sitompul Discrete Mathematics 1/25

Chapter 1 Logic and Proofs Equivalence of Compound Propositions n Two compound propositions A(p, q, …) and B(p, q, …) are said to be logically equivalent if they have identical truth table. n Notation: A(p, q, …) B(p, q, …) n Equivalent propositions are important for logical reasoning since they can be substituted and can help us to make simplification, make logical argument, infer new propositions, n Example: De Morgan’s Law (p q) p q F F F T T T F T F F T T p q T T F F F President University Erwin Sitompul Discrete Mathematics 1/26

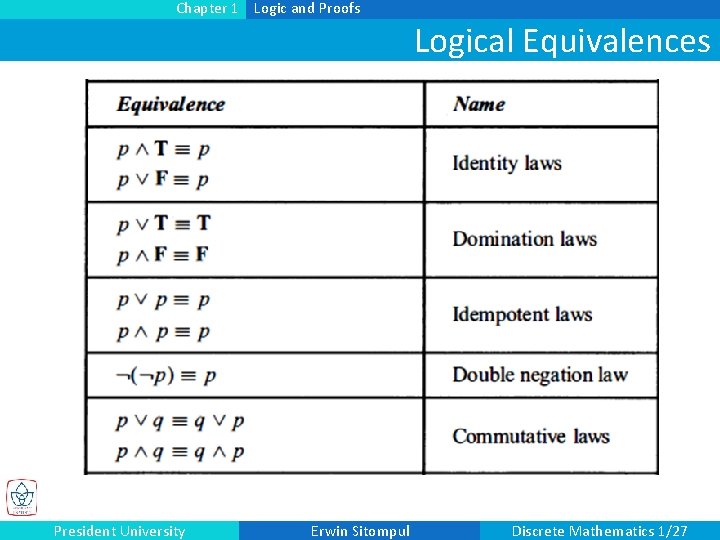
Chapter 1 Logic and Proofs Logical Equivalences President University Erwin Sitompul Discrete Mathematics 1/27

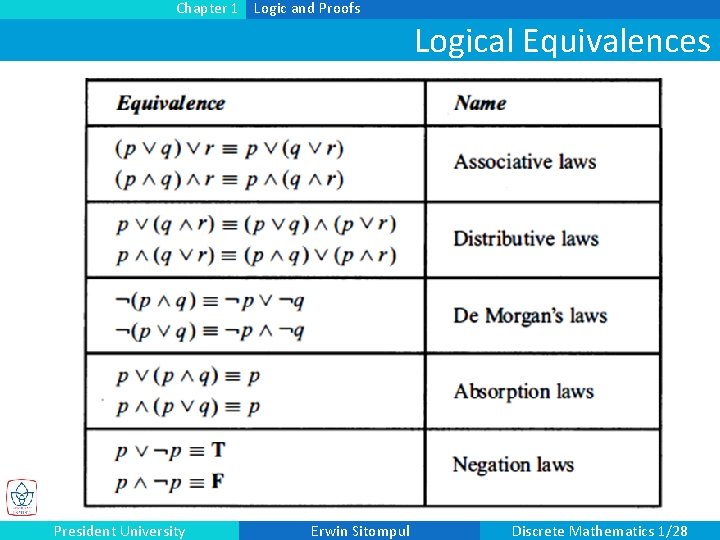
Chapter 1 Logic and Proofs Logical Equivalences President University Erwin Sitompul Discrete Mathematics 1/28

Chapter 1 Logic and Proofs Logical Equivalences n Example: Show that p (p q) and p q are logically equivalent. p (p q ) p ( p q) (De Morgan’s Law) (p p) (p q) (Distributive Law) T (p q) (Negation Law) p q (Identity Law) n Example: Negate the following proposition with De Morgan’s Law “The summer in Mexico is cold and sunny. ” (p q) p q President University Erwin Sitompul Discrete Mathematics 1/29

Chapter 1 Logic and Proofs Logical Equivalences n Example: Proof the truth of Absorption Law p (p q) p. p (p q) (p F) (p q) (Identity Law) p (F q) (Distributive Law) p F (Domination Law) p (Identity Law) President University Erwin Sitompul Discrete Mathematics 1/30

Chapter 1 Logic and Proofs Exclusive Disjunction n Let p and q are propositions. The proposition “p exclusive or q”, denoted by p q, is true when exactly one of p and q is true and is false otherwise. ● Exclusive Disjunction President University p q T T F T F T T F F F Erwin Sitompul Discrete Mathematics 1/31

Chapter 1 Logic and Proofs Conditional Proposition n Conditional proposition is also called implication. n Notation: p q n The way to pronounce: “if p, then q” ● Conditional (Implication) p q T T F F F T T F F T n In p q, the proposition p as called hypothesis or premise, and the proposition q is called conclusion or consequence. President University Erwin Sitompul Discrete Mathematics 1/32

Chapter 1 Logic and Proofs Conditional Proposition n Various ways to express implication p q: n If p, then q. n If p, q. n p implies/causes q. n q if p. n p only if q. n p is the sufficient condition for q. n p is sufficient for q. n q is the necessary condition for p. n q is necessary for p. n q whenever p. President University Erwin Sitompul Discrete Mathematics 1/33

Chapter 1 Logic and Proofs Conditional Proposition n Example: F T “If Albert Einstein is still alive then man ever walked on the moon. ” n Example: T F “If now is 2016 then Indonesia is already independent for 80 years. ” T F n Example: (Truth value still cannot be determined) n “If I pass the exams, then I will give you my notebook. ” n “If the temperature reaches 80 °C, then the alarm will buzz. ” n “If you have not enrolled properly, then your name will not be printed on the attendance list. ” President University Erwin Sitompul Discrete Mathematics 1/34

Chapter 1 Logic and Proofs Conditional Proposition n Example: Implication in various forms n “If today is rainy, then the flowers will grow well. ” n “If the gas pedal is pressed deeper, the car moves faster. ” n “Ice melted in north and south pole causes the increase of sea level. ” n “He is willing to go if he is given travel allowance. ” n “Andy can take Computer Organization only if he already passed Discrete Mathematics. ” n “The sufficient condition for a gas station to explode is small cigarette sparks. ” n “The necessary condition for Indonesia to win the World Cup is by hiring a famous foreign trainer. ” ● Convert all propositions above into “If p then q. ” President University Erwin Sitompul Discrete Mathematics 1/35

Chapter 1 Logic and Proofs Conditional Proposition n Example: Show that p q is logically equivalent with p q. p q p p q T T T F F F T T T “If p, then q” “Not p or q” n Example: Determine the negation of p q. (p q) ( p) q p q President University Erwin Sitompul Discrete Mathematics 1/36

Chapter 1 Logic and Proofs Conditional Proposition n Example: Express the following proposition combinations using symbolic notation. i. “You can access the internet from campus only if a (s g) you are a student or you are not a university guest. ” ii. “You cannot ride the roller coaster if you are under (u o) r 100 cm tall unless you are older than 16 years old. ” President University Erwin Sitompul Discrete Mathematics 1/37

Chapter 1 Logic and Proofs Conditional Proposition n Example: Assume two elementary propositions, p: “You drive over 100 km/h. ” q: “You get a speeding ticket. ” Translate each of these sentences to logic. i. “You do not drive over 100 km/h. ” ii. “You will get a speeding ticket if you drive over 100 km/h. ” iii. “If you do not drive over 100 km/h then you will not get a speeding ticket. ” iv. “Driving over 100 km/h is sufficient for getting a speeding ticket. ” v. “You get a speeding ticket, although you do not drive over 100 km/h. ” vi. “You drive over 100 km/h, but you do not get a speeding ticket. ” i. p ii. p q iv. p q President University iii. p q v. q p Erwin Sitompul vi. p q Discrete Mathematics 1/38

Chapter 1 Logic and Proofs Application of Propositional Logic n Inference and Reasoning: new true propositions are inferred from existing ones. n Used in the fields of: n Artificial Intelligence build programs that act intelligently, often rely on symbolic manipulations. n Rule based (expert) systems encode knowledge about the world in logic, new facts are inferred from existing facts following the semantics of logic. n Automatic theorem proof encode existing knowledge (e. g. about math) using logic and show that some hypothesis is true. President University Erwin Sitompul Discrete Mathematics 1/39

Chapter 1 Logic and Proofs Homework 1 1. Two merchants publish new marketing campaign to attract more customers. The first merchant launches a motto “Good stuffs are not cheap. ” The second merchants says “Cheap stuffs is not good. ” a) Examine whether both mottos tell the same message or not. b) In your opinion, which motto is better? President University Erwin Sitompul Discrete Mathematics 1/40

Chapter 1 Logic and Proofs Homework 1 A 1. Examine the statements S 1 and S 2, and find out whether they are logically equivalent or not. S 1: “Excellent physical condition is the necessary condition to become a soldier. ” S 2: “If someone does not have excellent physical condition, then he cannot become a soldier. ” 2. Show that p q q p by using (i) logical equivalences; (ii) truth table. President University Erwin Sitompul Discrete Mathematics 1/41