Discrete Mathematics is Essential Mathematics in the 21

Discrete Mathematics is Essential Mathematics in the 21 st Century: Rationale and Examples for High School NCTM 2009 Eric W. Hart

Time Magazine - Natl Standards “For example, I learned a lot of calculus, which hasn't proved that useful in my career. But I do remember being confronted at a Time Inc. meeting on digital strategy with the simple question of how many direct two-way links there were in a fully connected network of 50 nodes. It was a long time before any of us could figure out even how to begin figuring it out. Tomorrow's careers are likely to require more knowledge of networks, probabilities, statistics and risk analysis. ” – Walter Isaacson, Time Magazine, 4/15/09

Discrete Mathematics • What • Why • How/Where

What is Discrete Mathematics?

Three major topics in PSSM • Combinatorics systematic listing and counting • Iteration and recursion sequential step-by-step change • Vertex-edge graphs modeling paths and networks

Solve problems like … • How many different computer passwords can be created with five letters and two numbers? (Combinatorics) • How fast does money or a population grow? (Recursion and Iteration) • What is an optimal route for plowing snow from neighborhood streets? (Vertex-Edge Graphs)

Other DM Problems & Topics • When buying music on the Internet, how can you efficiently find the song, securely pay for it online, and efficiently download it? (Mathematics of Information Processing) • When electing a new mayor, how can you most accurately reflect voters’ opinions and avoid costly runoffs? (Mathematics of Democratic Decision Making) • Organize information in rectangular arrays of rows and columns (Matrices)

Key Themes of DM • Discrete Mathematical Modeling • Optimization • Algorithmic Problem Solving

Why Discrete Mathematics? • Useful — Widely used in business, industry, and government • Contemporary — particularly relevant in today’s digital information age • Educationally Powerful — problem solving, modeling, reasoning, representing, engaging, and provides students success doing mathematics

Discrete Mathematics for All “Discrete mathematics should be an integral part of the school mathematics curriculum. ” (NCTM, 2000, p. 13)

How/Where? • Integrate DM into other strands and courses – Vertex-Edge Graphs geometry – Recursion algebra and geometry – Math and voting Social Studies – DM topics richer Consumer or General Mathematics courses • Separate DM course – 4 th year course alternative to precalculus – DM and Stat course

How/Where? • National Recommendations – NCTM – Achieve • State Standards – IA – NJ – MN – AZ – other

NCTM Navigations Books on Discrete Mathematics Navigating through Discrete Mathematics in Pre. K-5 and Navigating through Discrete Mathematics in 6 -12

Navigating through Discrete Mathematics in Pre. K-12 • Focus: how to implement PSSM’s recommendation that “discrete mathematics should be an integral part of the school mathematics curriculum” • 6 -12 Book • Pre. K-5 Book • Detailed grade-specific recommendations • Classroom activities • Mathematics background

Pre. K-5 Book 1. 2. 3. 4. 5. 6. Introduction Counting Pre. K-2 Counting 3 -5 Vertex-Edge Graphs Pre. K-2 Vertex-Edge Graphs 3 -5 Iteration and Recursion Pre. K-2 Iteration and Recursion 3 -5

6 -12 Book 1. 2. 3. 4. 5. 6. Introduction Counting 6 -8 Counting 9 -12 Vertex-Edge Graphs 6 -8 Vertex-Edge Graphs 9 -12 Iteration and Recursion 6 -8 Iteration and Recursion 9 -12

Recursion

Recursive View of Functions • Linear • Exponential • Polynomial

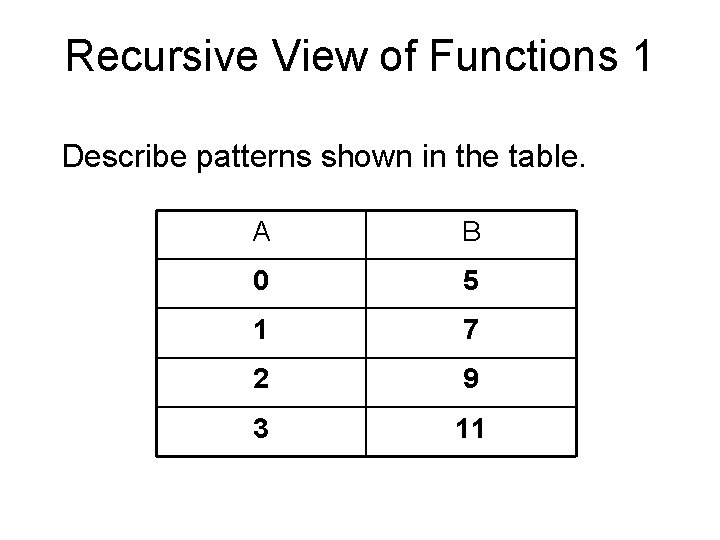
Recursive View of Functions 1 Describe patterns shown in the table. A B 0 5 1 7 2 9 3 11

Look down the column of B’s NEXT = NOW + 2 Bn+1 = Bn + 2 A B 0 5 1 7 2 9 3 11

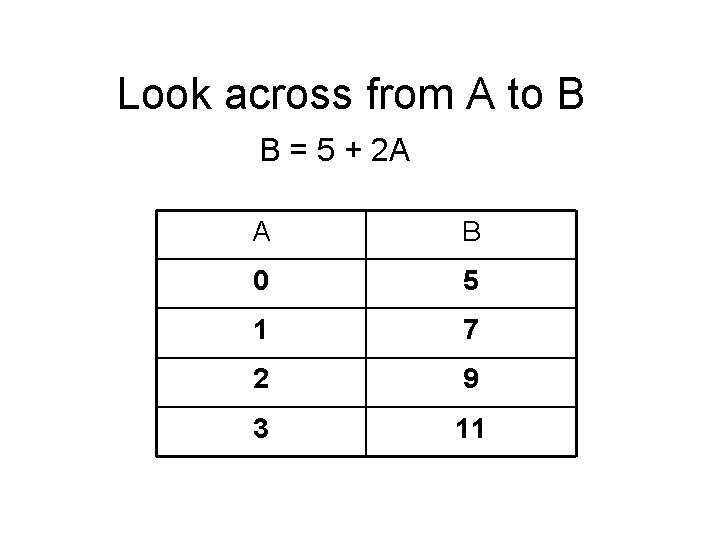
Look across from A to B B = 5 + 2 A A B 0 5 1 7 2 9 3 11

Recursive View of Linear Functions • Explicit form: B = 5 + 2 A • Recursive form: § NEXT = NOW + 2, start at 5 § Bn+1 = Bn + 2, B 0 = 5 • Slope seen concretely in recursive form • Rate of Change seen concretely • Note also: arithmetic sequence

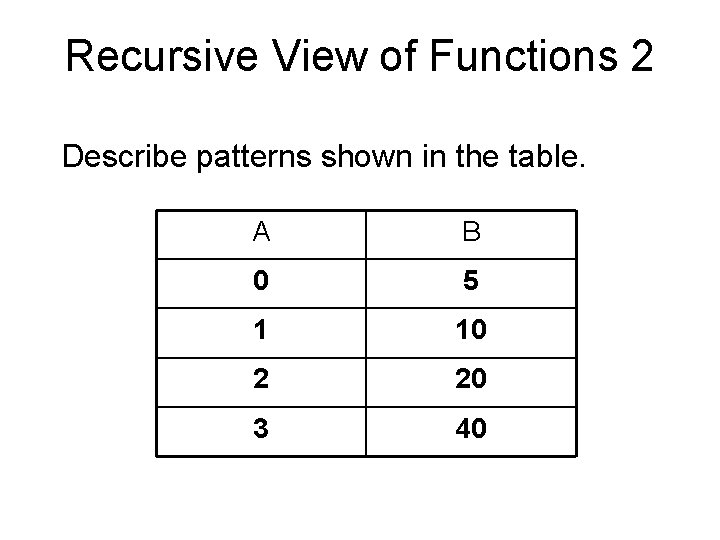
Recursive View of Functions 2 Describe patterns shown in the table. A B 0 5 1 10 2 20 3 40

Look down the column of B’s NEXT = NOW * 2 Bn+1 = Bn * 2 A B 0 5 1 10 2 20 3 40

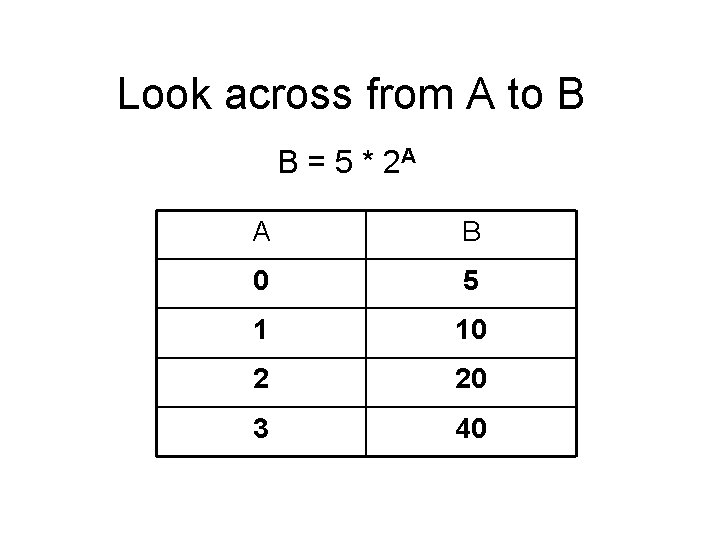
Look across from A to B B = 5 * 2 A A B 0 5 1 10 2 20 3 40

Recursive View of Exponential Functions • Explicit form: B = 5 * 2 A • Recursive form: § NEXT = NOW * 2, start at 5 § Bn+1 = Bn * 2, B 0 = 5 • Potent comparison to linear – add constant vs. multiply by constant at each step • Note also: geometric sequence

Common Applications Linear and Exponential Recursive point of view gives powerful information and insights Distance-Rate-Time Compound Interest Distance traveled from DT Money saved: $1000 initial Chicago: 1 hr to get out of town deposit, 6% interest (30 mi), then cruise at 70 mph compounded annually Represent each situation with a table, graph, and equations (recursive and explicit)

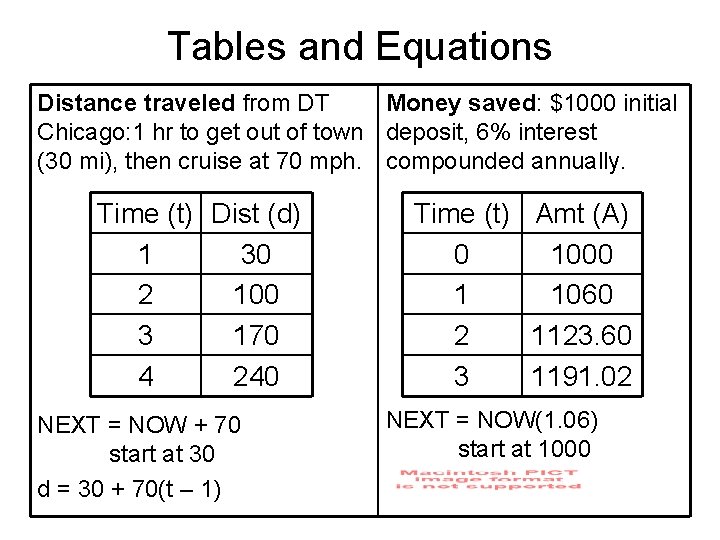
Tables and Equations Distance traveled from DT Money saved: $1000 initial Chicago: 1 hr to get out of town deposit, 6% interest (30 mi), then cruise at 70 mph. compounded annually. Time (t) Dist (d) 1 30 2 100 3 170 4 240 NEXT = NOW + 70 start at 30 d = 30 + 70(t – 1) Time (t) Amt (A) 0 1000 1 1060 2 1123. 60 3 1191. 02 NEXT = NOW(1. 06) start at 1000

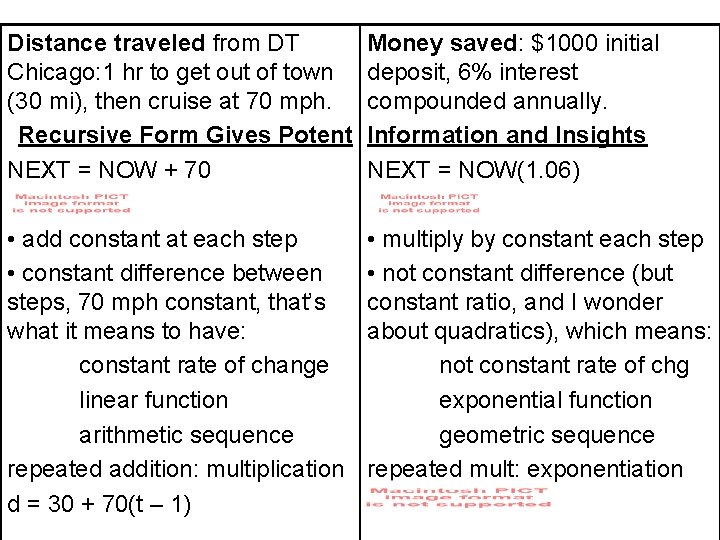
Distance traveled from DT Chicago: 1 hr to get out of town (30 mi), then cruise at 70 mph. Recursive Form Gives Potent NEXT = NOW + 70 Money saved: $1000 initial deposit, 6% interest compounded annually. Information and Insights NEXT = NOW(1. 06) • add constant at each step • constant difference between steps, 70 mph constant, that’s what it means to have: constant rate of change linear function arithmetic sequence repeated addition: multiplication d = 30 + 70(t – 1) • multiply by constant each step • not constant difference (but constant ratio, and I wonder about quadratics), which means: not constant rate of chg exponential function geometric sequence repeated mult: exponentiation

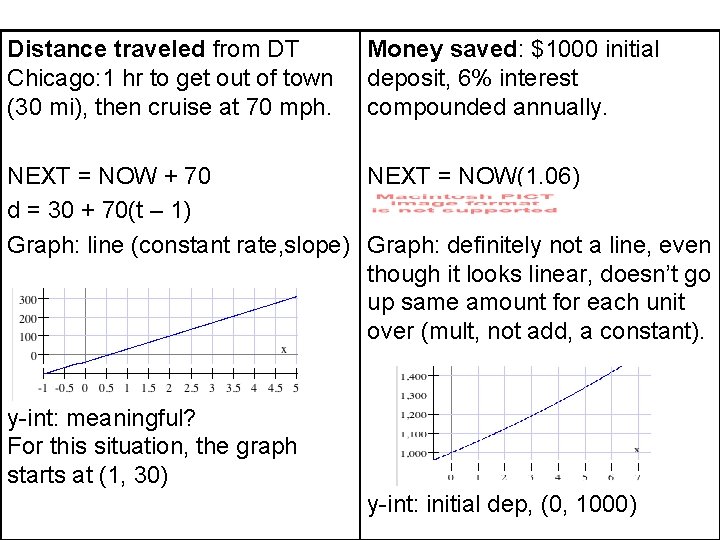
Distance traveled from DT Chicago: 1 hr to get out of town (30 mi), then cruise at 70 mph. Money saved: $1000 initial deposit, 6% interest compounded annually. NEXT = NOW + 70 NEXT = NOW(1. 06) d = 30 + 70(t – 1) Graph: line (constant rate, slope) Graph: definitely not a line, even though it looks linear, doesn’t go up same amount for each unit over (mult, not add, a constant). y-int: meaningful? For this situation, the graph starts at (1, 30) y-int: initial dep, (0, 1000)

Common Applications Linear and Exponential Recursive point of view gives powerful information and insights Distance-Rate-Time Compound Interest Distance traveled from DT Money saved: $1000 initial Chicago: 1 hr to get out of town deposit, 6% interest (30 mi), then cruise at 70 mph. compounded annually.

Recursive View of Functions 3 Describe patterns shown in the table….

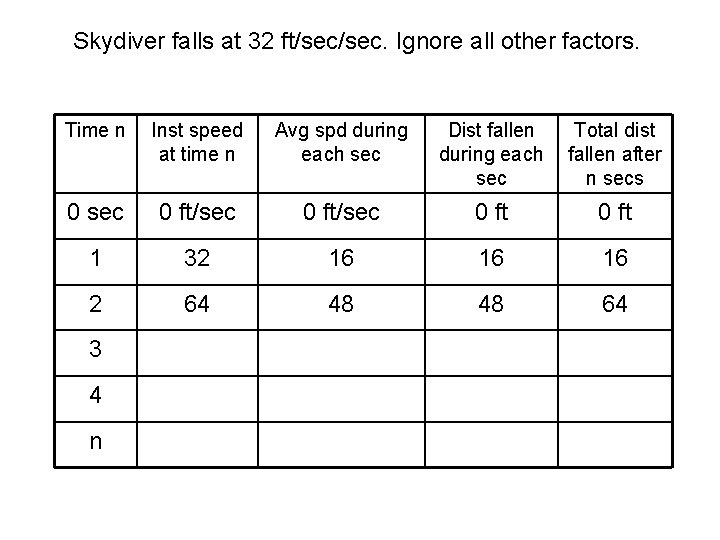
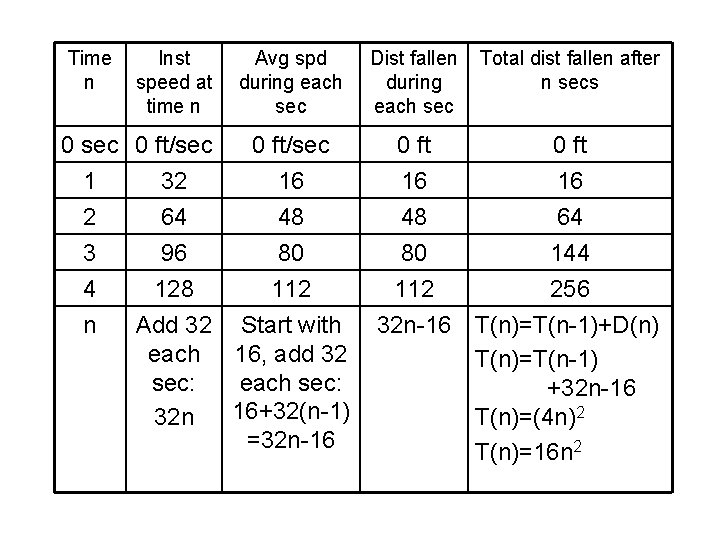
Skydiver falls at 32 ft/sec. Ignore all other factors. Time n Inst speed at time n Avg spd during each sec Dist fallen during each sec Total dist fallen after n secs 0 sec 0 ft/sec 0 ft 1 32 16 16 16 2 64 48 48 64 3 4 n

Time n Inst speed at time n 0 sec 0 ft/sec 1 32 2 3 4 n Avg spd during each sec Dist fallen during each sec Total dist fallen after n secs 0 ft/sec 16 0 ft 16 64 48 96 80 128 112 Add 32 Start with each 16, add 32 sec: each sec: 16+32(n-1) 32 n =32 n-16 48 64 80 144 112 256 32 n-16 T(n)=T(n-1)+D(n) T(n)=T(n-1) +32 n-16 T(n)=(4 n)2 T(n)=16 n 2

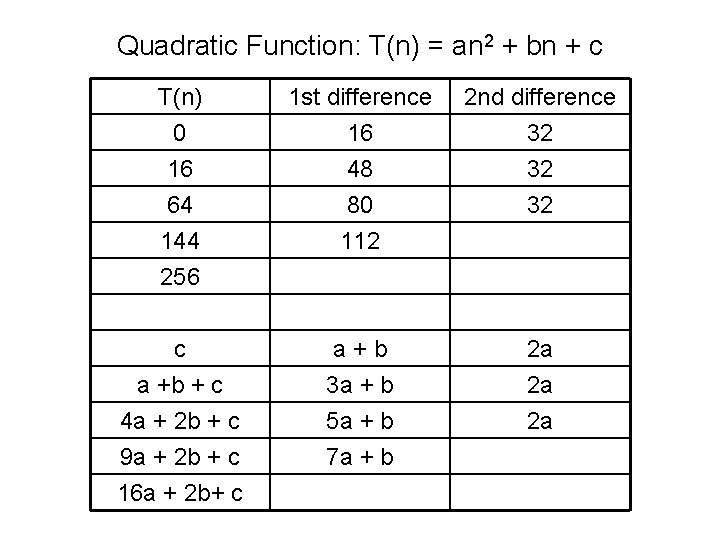
Quadratic Function: T(n) = an 2 + bn + c T(n) 0 16 64 1 st difference 16 48 80 144 256 112 c a +b + c 4 a + 2 b + c 9 a + 2 b + c 16 a + 2 b+ c a+b 3 a + b 5 a + b 7 a + b 2 nd difference 32 32 32 2 a 2 a 2 a

Recursive View of Functions • Linear • Exponential • Polynomial

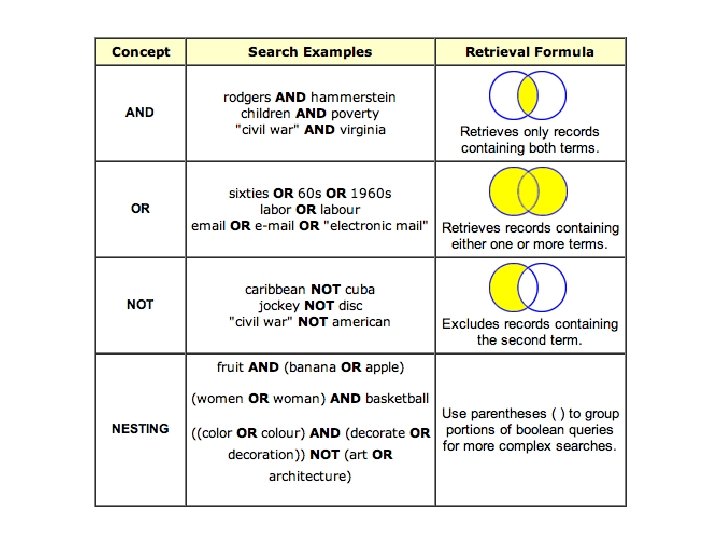
Set Theory and Logic Example: Internet Searching Library of Congress Online Catalog • Help page on “Boolean Operators” http: //catalog. loc. gov/help/boolean. htm • AND, OR, NOT • Venn diagrams

Modular Arithmetic Examples: • Check digits for ID Numbers – UPC – ISBN – Credit Cards • Cryptography – Secure online transactions – Encrypted email or file storage

12 -Digit UPC Check Digit Algorithm: 1. 3 (sum of even position digits) + (sum of odd position digits) RIGHT-TO-LEFT 2. Equivalent to 0 mod 10? Yes? OK. No? Error. Note: Use all 12 digits in the algorithm. Last digit is is the check digit. Check digit is chosen to make the result = 0 mod 10. Try it: 0 -49387 -10018 -7

Cryptography “the science of transmitting and managing information in the presence of an adversary” (Koblitz, AMS Notices, Sept, 2007) Mathematics: modular arithmetic, number theory, abstract algebra

Cryptography on the Internet

Cryptography on the Internet

RSA Public-Key Crypto • Everyone knows the public encryption key • Only the designated recipient knows the secret decryption key • Works and is secure because it’s easy to multiply two numbers, but hard to factor a number

RSA method • Multiply 2 large primes, p and q, to get a large composite number, n. • Compute r = (p – 1)(q – 1) • Find a number e (for encrypt) that has a multiplicative inverse d (for decrypt) under multiplication mod r. • Encrypt: raise to power e, reduce mod n • Decrypt: raise to power d, reduce mod n • Public encryption key – e and n Private decryption key – d

RSA method works because: • Special case of Euler’s Theorem: (Me)d = M mod n • To break the code, an adversary would need to factor the very large number n, and factoring is hard. (Factoring n would give p and q, which would give r, which would give d, since e is public, and thus the message could be decrypted. )

Modular Arithmetic Examples: • Check digits for ID Numbers – UPC – ISBN – Credit Cards • Cryptography – Secure online transactions – Encrypted email or file storage

Vertex-Edge Graphs • Diagrams consisting of points (vertices) and segments or arcs (edges) joining some of the points. • Connections matter, not size and shape • Model and solve problems related to – Networks – Paths – Relationships among a finite # of objects (like conflict or prerequisite relationships)

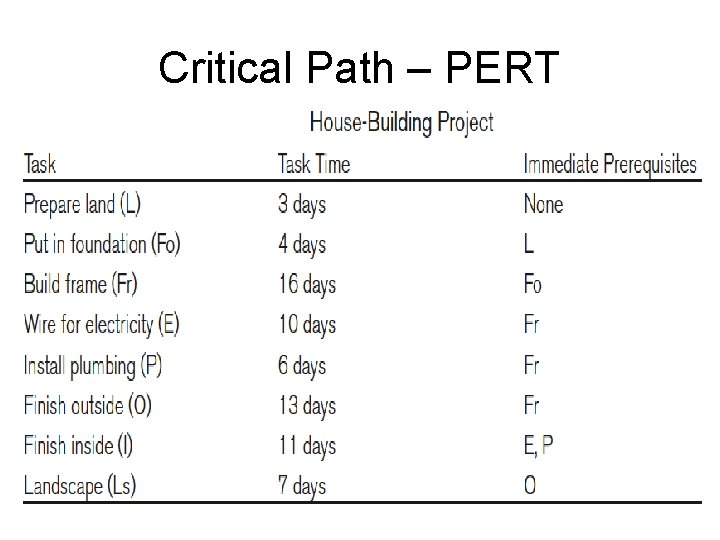
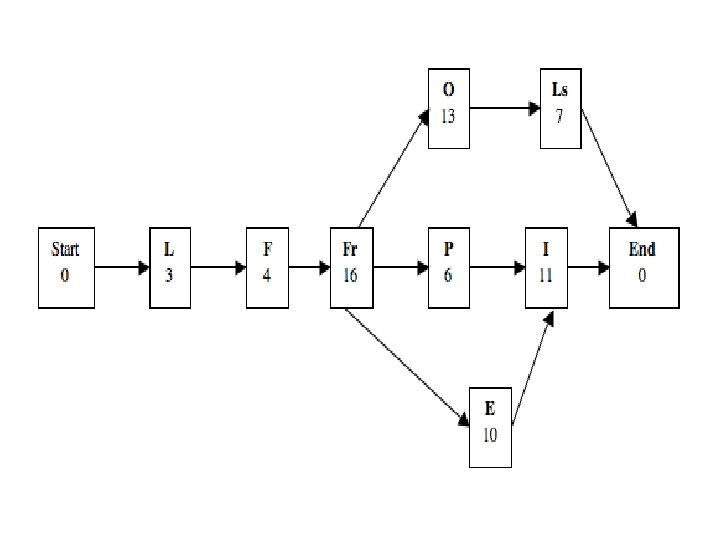
Critical Path – PERT

Discrete Mathematics is Essential Mathematics for All Students • Counting – How many? • Recursion – Sequential change • Vertex-Edge Graphs – Networks, paths, relationships • Set Theory, Logic, Modular Arithmetic – Math of information processing & the Internet • Math and Voting – Preferential voting