Discrete Mathematics for Computer Science COMPSCI 230 Duke

Discrete Mathematics for Computer Science COMPSCI 230 Duke University Randomness and Computation: Some Prime Examples

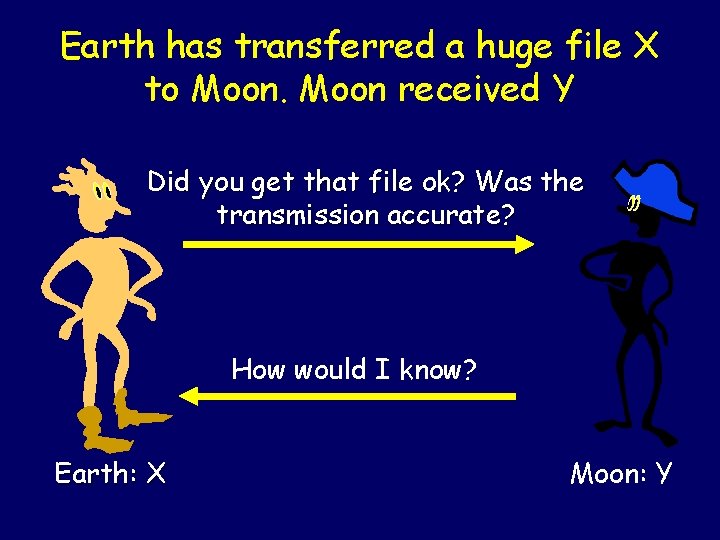
Earth has transferred a huge file X to Moon received Y. Did you get that file ok? Was the transmission accurate? How would I know? Earth: X Moon: Y

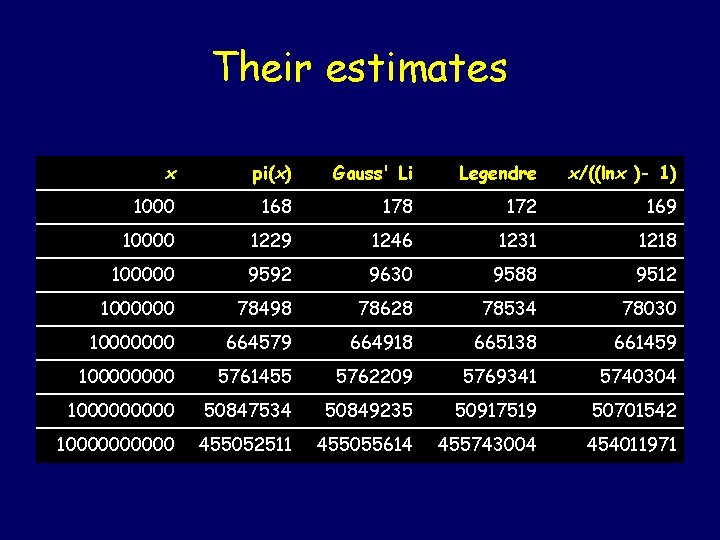
Legendre Let (n) be the number of primes between 1 and n. I wonder how fast (n) grows? Conjecture [1790 s]: Gauss

Their estimates x pi(x) Gauss' Li Legendre x/((lnx )- 1) 1000 168 172 169 10000 1229 1246 1231 1218 100000 9592 9630 9588 9512 1000000 78498 78628 78534 78030 10000000 664579 664918 665138 661459 10000 5761455 5762209 5769341 5740304 100000 50847534 50849235 50917519 50701542 100000 455052511 455055614 455743004 454011971

De la Vallée Poussin J-S Hadamard Two independent proofs of the Prime Density Theorem [1896]:

The Prime Density Theorem This theorem remains one of the celebrated achievements of number theory. In fact, an even sharper conjecture remains one of the great open problems of mathematics!

The Riemann Hypothesis [1859] Riemann

Slightly easier to show (n)/n ≥ 1/(2 log n) (We’ll use this, but won’t prove it here. )

Random (log n)-bit number is a random number from 1. . n (just add one) (n) / n ≥ 1/(2 log n) means that a random (log n)-bit number has at least a 1/2 log n chance of being prime.

Random k-bit number is a random number from 1. . 2 k (2 k) / 2 k ≥ 1/2 k means that a random k-bit number has at least a 1/2 k chance of being prime.

Really useful fact A random k-bit number has at least a 1/2 k chance of being prime. So if we pick 2 k random k-bit numbers the expected number of primes on the list is at least 1

Picking A Random Prime Many modern cryptosystems (e. g. , RSA) include the instructions: “Pick a random n-bit prime. ” How can this be done efficiently?

Picking A Random Prime “Pick a random n-bit prime. ” Strategy: 1) Generate random n-bit numbers 2) Test each one for primality [more on this later in the lecture]

Tremendously Useful Inequality x, 1 + x ≤ ex (note: so for small x, 1 + x ≈ ex) Corollaries x, 1 – x ≤ e-x x≠ 0, 1 + 1/x ≤ e 1/x x>0, (1 + 1/x)x ≤ e x≠ 0, 1 - 1/x ≤ e-1/x x>0, (1 - 1/x)x ≤ 1/e

Picking A Random Prime “Pick a random n-bit prime. ” 1)Generate kn random n-bit numbers Each trial has a ≥ 1/2 n chance of being prime. Pr[ all kn trials yield composites ] ≤ (1 -1/2 n)kn = (1 -1/2 n)2 n * k/2 ≤ 1/ek/2

Picking A Random Prime “Pick a random n-bit prime. ” Strategy: 1) Generate random n-bit numbers 2) Test each one for primality For 1000 -bit primes, if we try out 10000 random 1000 -bit numbers, chance of failing ≤ e-5 ≤. 0068

Moral of the story Picking a random prime is “almost as easy as” picking a random number. (Provided we can check for primality. )

Checking for Primality Fermat’s Little Theorem: An integer n > 1 is prime if and only if an-1 1 (mod n) for all a such that 1 ≤ a ≤ n-1 “Fake Square Root of 1” Theorem: If a and n are positive integers such that a 2 1 (mod n) but a 1 (mod n) then n is composite

Miller-Rabin Randomized Primality Test If n > 2 and n is even, return “composite” Pick a uniformly at random from {1, 2, …, n-1} If an-1 1 (mod n), return “composite” Let n-1 = t 2 s for some s > 0 and odd t For i = 1, 2, …, s it i-1 t 2 2 if a 1 (mod n) but a 1 (mod n) return “composite” Return “passed test”

Monte Carlo Algorithm The Miller-Rabin randomized primality test might return “passed test” even when the number is actually composite!

What does the test tell us? If n is prime, the test says “passed test” If n is composite, the test says “composite” with probability at least ¾ “passed test” with probability at most ¼ I. e. , the answer is incorrect with probability at most ¼ If n is composite and the test is run k times, the probability that it says “passed test” each time is at most (1/4)k. If the test ever says “composite” the number is composite.

Earth has transferred a huge file X to Moon received Y Did you get that file ok? Was the transmission accurate? How would I know? Earth: X Moon: Y

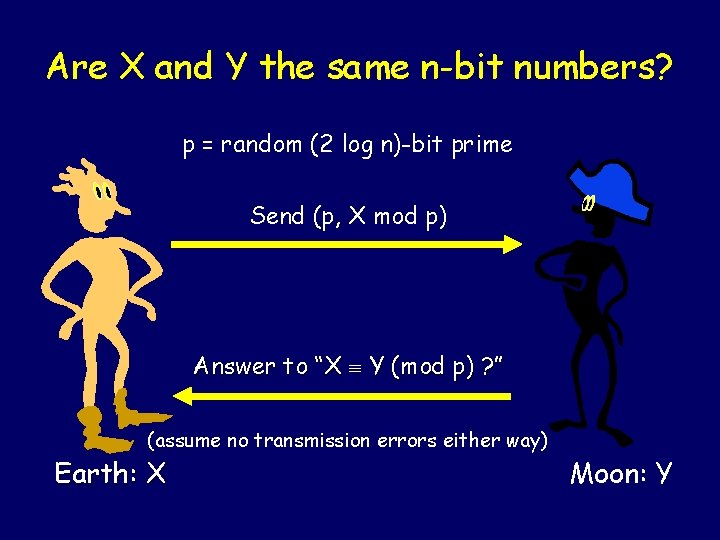
Are X and Y the same n-bit numbers? p = random (2 log n)-bit prime Send (p, X mod p) Answer to “X Y (mod p) ? ” (assume no transmission errors either way) Earth: X Moon: Y

Why is this any good? Easy case: If X = Y, then X Y (mod p) and answer to “X Y (mod p) ? ” is Yes!

Why is this any good? Harder case: What if X Y? We want answer to “X Y (mod p) ? ” to be No! But answer is Yes! if X Y (mod p), i. e. , p | (X-Y) How likely is this? Define Z = (X-Y). To mess up, p must divide Z. Z is an n-bit number Z is at most 2 n. But each prime is ≥ 2. Hence Z has at most n prime divisors.

Almost there… Z has at most n prime divisors. How many (2 log n)-bit primes are there? Recall (2 k) ≥ 2 k /2 k at least 22 logn/2*2 log n = n 2/(4 log n) >> 2 n primes. At most half of them divide Z. Hence the probability that a random (2 log n)-bit prime divides Z is at most ½. Make mistake (answer Yes!) with probability at most ½.

Theorem: Let X and Y be distinct n-bit numbers. Let p be a random (2 log n)-bit prime. Then Prob [X = Y mod p] < 1/2 Earth-Moon protocol makes mistake with probability at most 1/2!

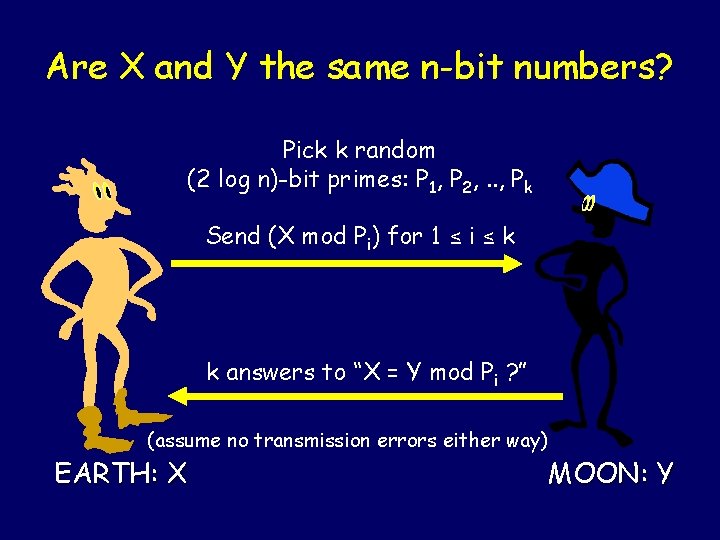
Are X and Y the same n-bit numbers? Pick k random (2 log n)-bit primes: P 1, P 2, . . , Pk Send (X mod Pi) for 1 ≤ i ≤ k k answers to “X = Y mod Pi ? ” (assume no transmission errors either way) EARTH: X MOON: Y

Exponentially smaller error probability If X=Y, always accept. If X Y, Prob [X = Y mod Pi for all i] ≤ (1/2)k