Discrete Mathematics Election Theory Unit Introduction Voting on

Discrete Mathematics Election Theory Unit

Introduction Voting on the surface seems really easy: • • • We hold an election. We count the ballots. We determine the outcome in a consistent and fair manner. In this unit you will learn: 1. 2. 3. Methods for collecting and recording votes Methods for counting votes and ranking candidates “Fairness Criterion” – what it means to be fair

Small Group Activity In your groups write these five soft drinks on a piece of paper: • Coke • Dr. Pepper • Mountain Dew • Pepsi • Sprite

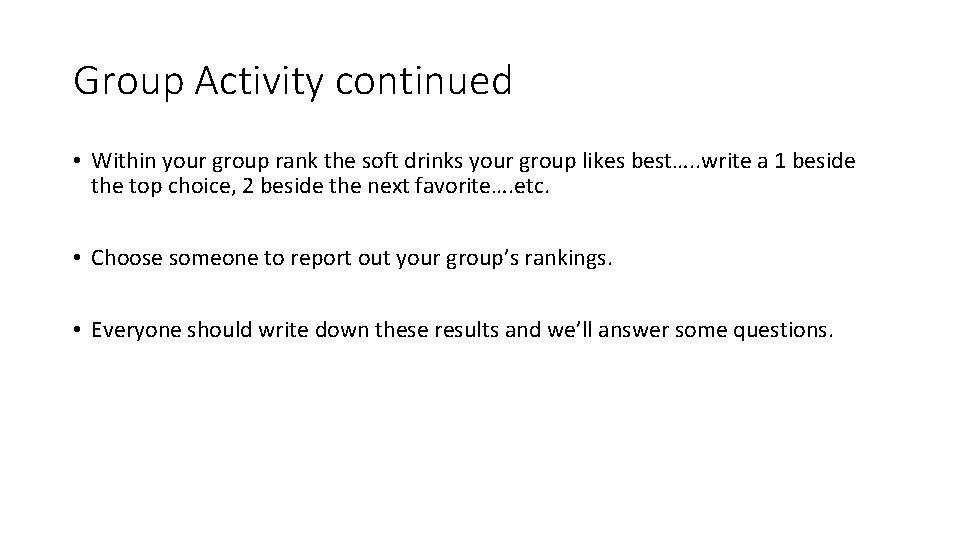
Group Activity continued • Within your group rank the soft drinks your group likes best…. . write a 1 beside the top choice, 2 beside the next favorite…. etc. • Choose someone to report out your group’s rankings. • Everyone should write down these results and we’ll answer some questions.

Group Activity Exercises 1. Do all the group rankings have the same drink ranked first? If not, which is ranked first most often? 2. Second? 3. Third? 4. Fourth? 5. Fifth?

Group Activity Exercise Let’s talk about how each group made their decisions on the rankings.

INDEPENDENTLY Rank These • Rank order the following sports in your groups from your favorite to your least favorite. • Basketball, Softball/Baseball, Football, Soccer • What’s another word for your “favorite”?

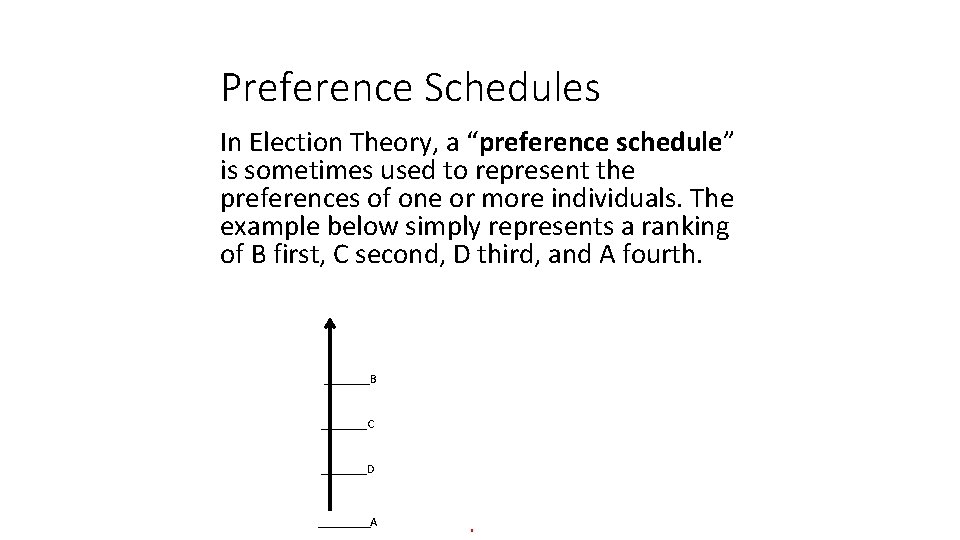
Preference Schedules In Election Theory, a “preference schedule” is sometimes used to represent the preferences of one or more individuals. The example below simply represents a ranking of B first, C second, D third, and A fourth. _______B _______C _______D ____A

Preference Schedules • In your groups, YOU ALREADY created a preference schedule of your results for the five soft drinks…. . • Within your groups, were there people who didn’t agree with your “group” ranking? • Those individuals would represent a different preference schedule.

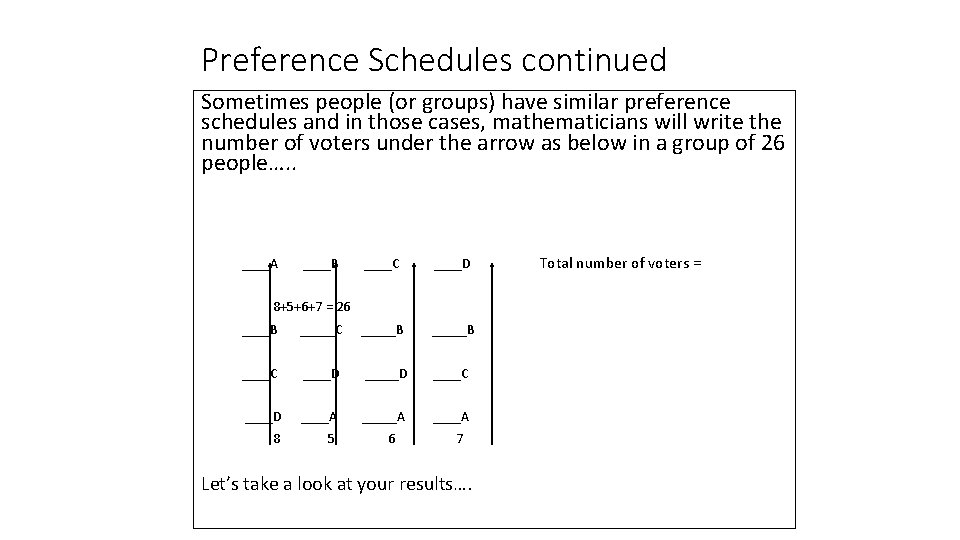
Preference Schedules continued Sometimes people (or groups) have similar preference schedules and in those cases, mathematicians will write the number of voters under the arrow as below in a group of 26 people…. . ____A ____B ____C ____D Total number of voters = 8+5+6+7 = 26 ____B _____C _____B ____C ____D ____C ____D ____A _____A 8 5 6 7 Let’s take a look at your results….

Preferential Ballot • A preferential ballot is one that allows voters to rank the choices. Where might you see another example in the real world? • Ideas/Examples? • Most of our elections in the US are not preferential ballots. Do you think they are a good idea? Why not?

You Practice • A survey was taken last or high school students asking them to rank order their three favorite fast food restaurants in the Concord area. The results were as follows: 35 students ranked Chik-fil-a first, Bojangles second and Cook-out third. 26 ranked Bojangles first followed by Zaxby’s and then Chick-fil-a. 17 ranked Mc. Donalds first and then Wendy’s and Chick-fil-a. • Create three Preference Schedules reflecting these survey results.

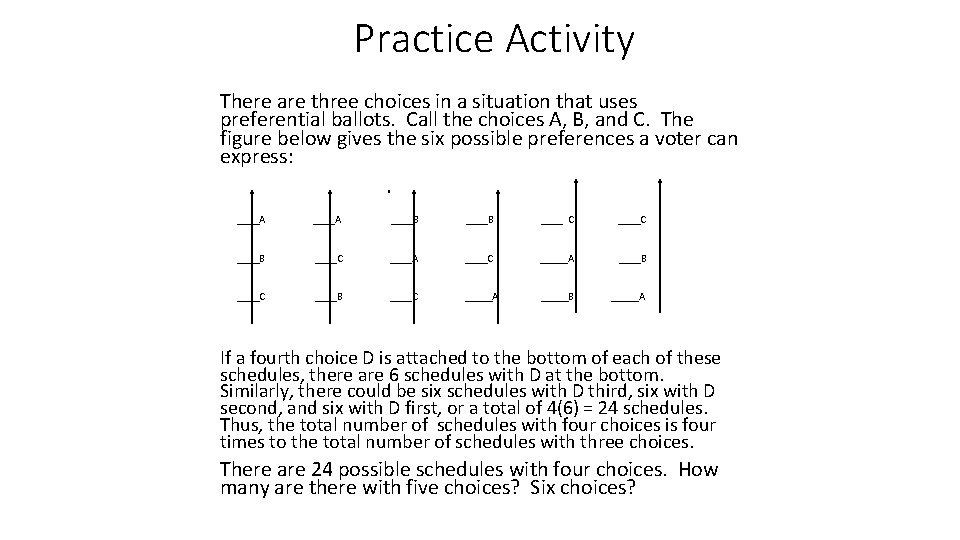
Practice Activity There are three choices in a situation that uses preferential ballots. Call the choices A, B, and C. The figure below gives the six possible preferences a voter can express: ____A ____B ____ C ____C ____B ____C ____A ____C _____A ____B ____C ____B ____C _____A _____B _____A If a fourth choice D is attached to the bottom of each of these schedules, there are 6 schedules with D at the bottom. Similarly, there could be six schedules with D third, six with D second, and six with D first, or a total of 4(6) = 24 schedules. Thus, the total number of schedules with four choices is four times to the total number of schedules with three choices. There are 24 possible schedules with four choices. How many are there with five choices? Six choices?

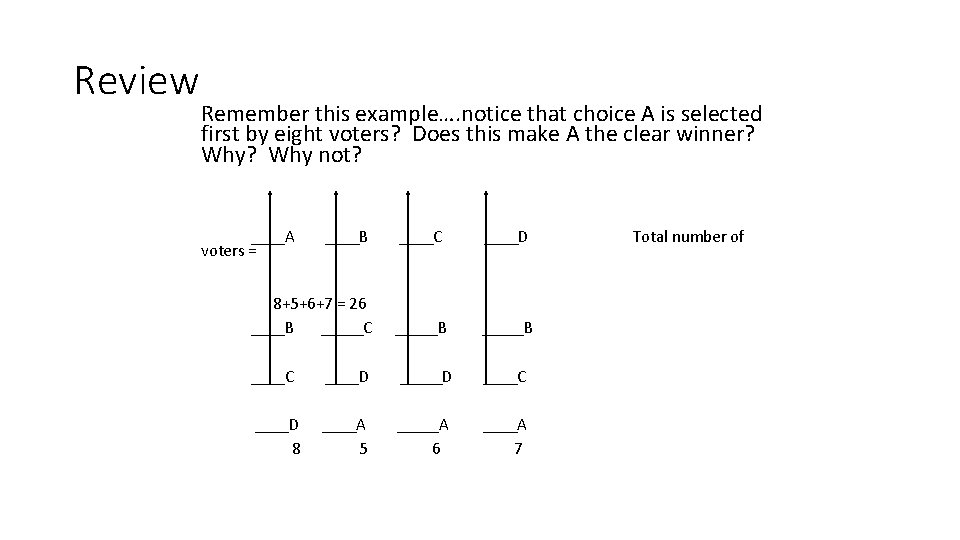
Review Remember this example…. notice that choice A is selected first by eight voters? Does this make A the clear winner? Why not? ____A ____B ____C ____D voters = 8+5+6+7 = 26 ____B _____C _____B ____C ____D ____C ____D ____A _____A 8 5 6 7 Total number of

Plurality Method • If A is the winner purely on the basis that A got the most first place votes, then A is called the “Plurality Winner” and the election method being used is called the “Plurality Method”. • What percent of the vote did A receive? • If A receives over 50% of the first place vote, then A is considered to be the “Majority Winner? ”

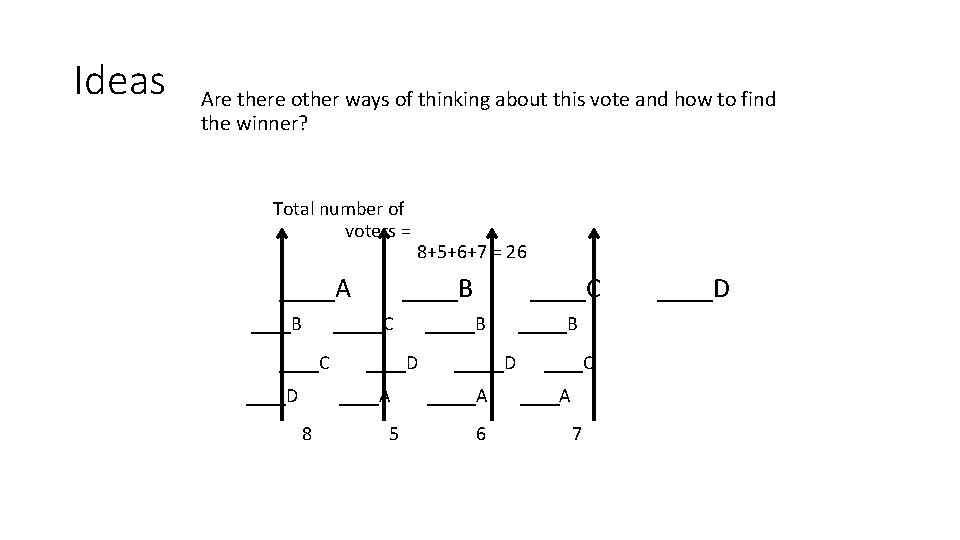
Ideas Are there other ways of thinking about this vote and how to find the winner? Total number of voters = 8+5+6+7 = 26 ____A ____B ____C ____D ____B _____C _____B ____C ____D _____D ____C ____D ____A 8 5 6 7

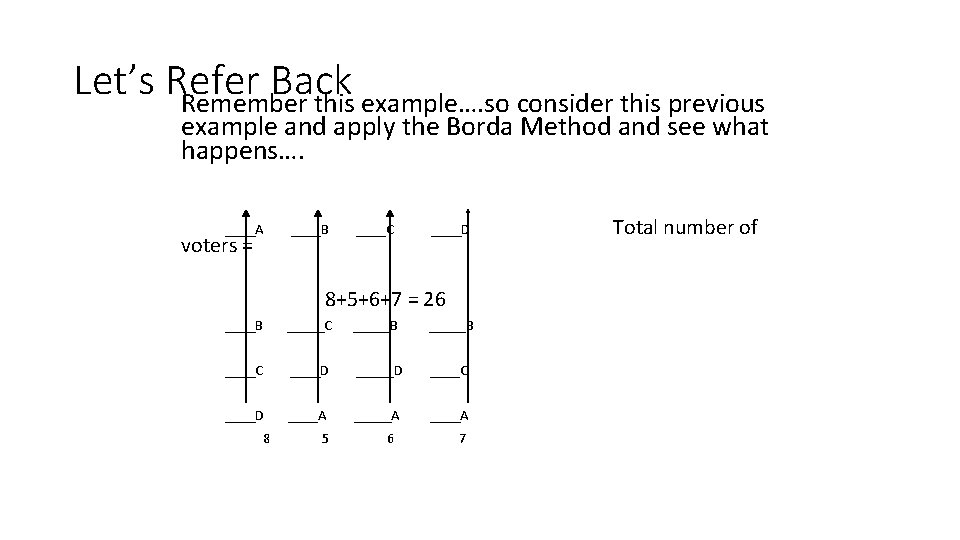
Borda Method Borda, a French mathematician and soldier was opposed to the plurality method and proposed what is now called the Borda Method or Borda Count. • Simply put, Borda assigned points to each place with the highest number of points being assigned to the top choice and reducing the points by one for each place. • Put that in mathematical terms…. . • If you have “n” choices, then you assign “n” points to a first-place ranking, n-1 to second and so on…. .

Let’s Refer Back Remember this example…. so consider this previous example and apply the Borda Method and see what happens…. ____A ____B ____C ____D voters = 8+5+6+7 = 26 ____B _____C _____B ____C ____D ____C ____D ____A _____A 8 5 6 7 Total number of

continued A: B: C: D:

continued Compare your results… A: 8(4) + 5(1) + 6(1) + 7(1) = 50 B: 8(3) + 5(4) + 6(3) + 7(3) = 83 C: 8(2) + 5(3) + 6(4) + 7(2) = 69 D: 8(1) + 5(2) + 6(2) + 7(4) = 58 So what do you notice? Thoughts? Fair or not fair?

Let’s Take an Example From Class Step 1: Preference Schedule Step 2: Plurality Method Results Step 3: Impose the Borda Method Step 4: Borda Method Results

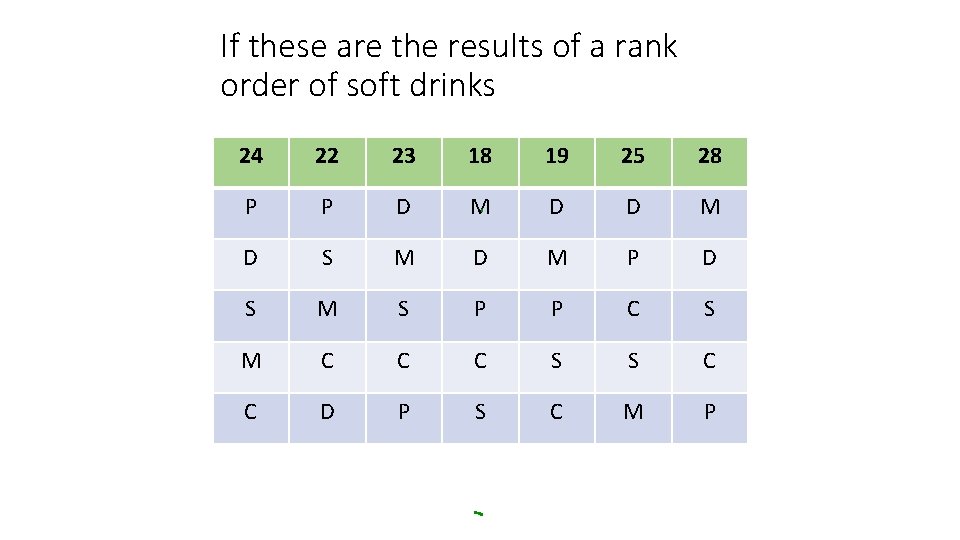
If these are the results of a rank order of soft drinks 24 22 23 18 19 25 28 P P D M D S M D M P D S M S P P C S M C C C S S C C D P S C M P

Literacy/research activity • Pick one of the following topics related to Election Theory and research the topic. Preference Balloting Preference Schedules Borda Method Sequential Runoff Method Plurality versus Majority Marquis de Condorcet Kenneth Arrow’s Conditions Weighted Voting Approval Voting • Then identify the five most important things you learn about your topic and create a Tri-Fold study guide that will help other students learn those five things. • Your product should be informative, descriptive, colorful, and contain examples/graphic organizers for the information you want to teach and remember.

Foldable project collection

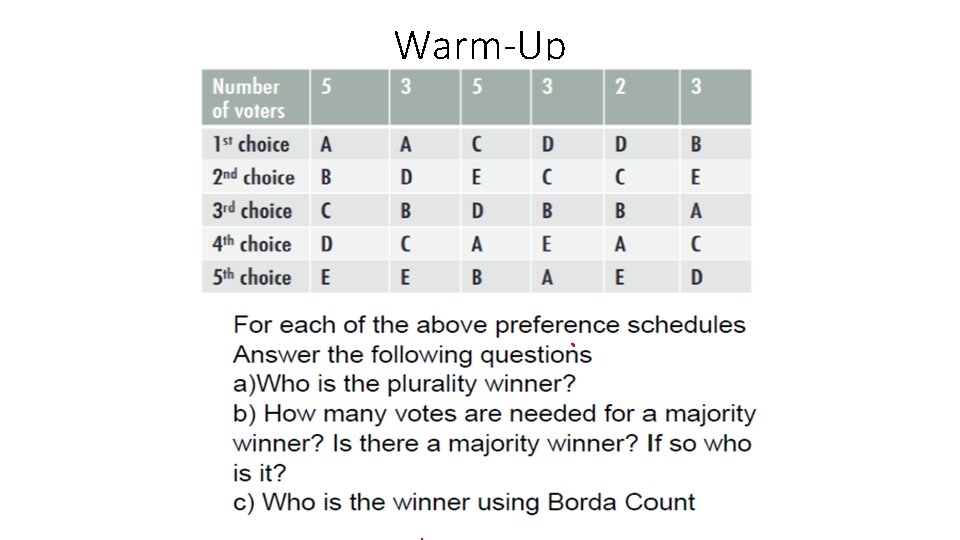
Warm-Up

Groups Jigsaw Activity • Consider the following four basketball players: • Steph Curry • Lebron James • Kevin Durant • James Harden Who do you think is the best player right now? Rank order the four from the greatest of all time to the third greatest. Which player wins?

What happens if nobody reaches a majority? • In a recent United States senate election, the sitting senator in Louisiana had two challengers on the ballot and received the plurality of the votes. However, some states (including Louisiana) and other municipalities require a majority of the votes to be considered the winner. • What happened?

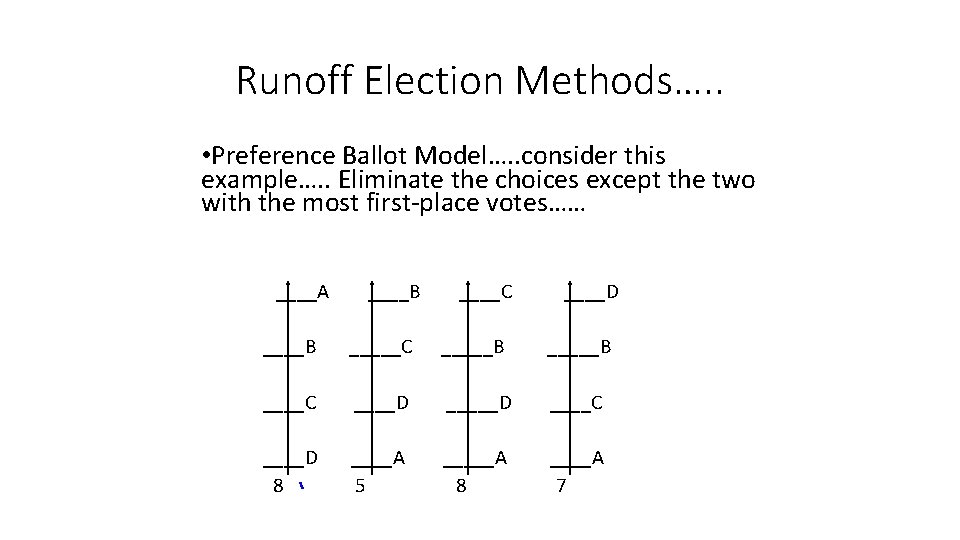
Runoff Election Methods…. . • Preference Ballot Model…. . consider this example…. . Eliminate the choices except the two with the most first-place votes…… ____A ____B ____C ____D ____B _____C _____B ____C ____D ____C ____D ____A _____A 8 5 8 7

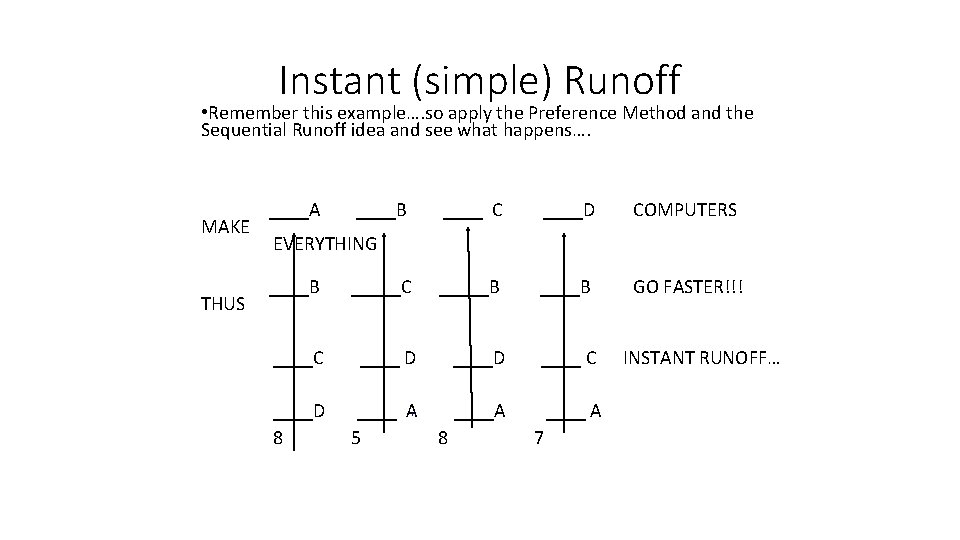
Instant (simple) Runoff • Remember this example…. so apply the Preference Method and the Sequential Runoff idea and see what happens…. ____A ____B ____ C ____D MAKE EVERYTHING COMPUTERS ____B _____C _____B ____B THUS GO FASTER!!! ____C ____ D ____ C INSTANT RUNOFF… ____D ____ A ____A ____ A 8 5 8 7

Sequential Runoff Method • The Sequential Runoff Method eliminates one choice at a time…. however if you have multiple choices and voters have to return multiple times…. . well, you tell me what would happen? • However, again, if we apply the Preference Ballot Model to the sequential method, let’s explore what happens……

continued • If you notice, we have now eliminated two candidates in the previous slide…. • Now what happens if you re-consider the voting results with just the two remaining candidates…. who wins? • So why don’t we use this method as a runoff method? What might be some of the advantages to using this method? What are the drawbacks? • Can you think of other runoff methods?

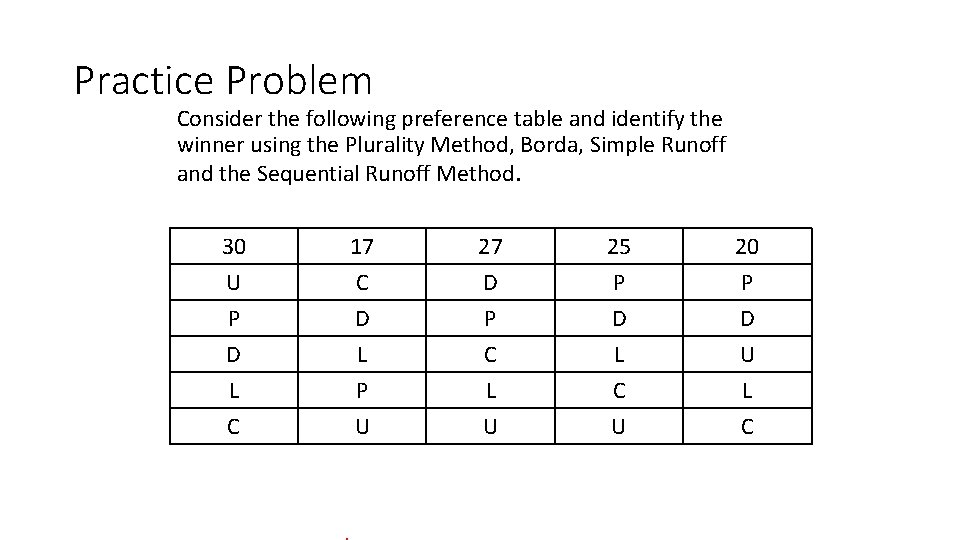
Practice Problem Consider the following preference table and identify the winner using the Plurality Method, Borda, Simple Runoff and the Sequential Runoff Method. 30 U P D 17 C D L 27 D P C 25 P D L 20 P D U L C P U L U C U L C

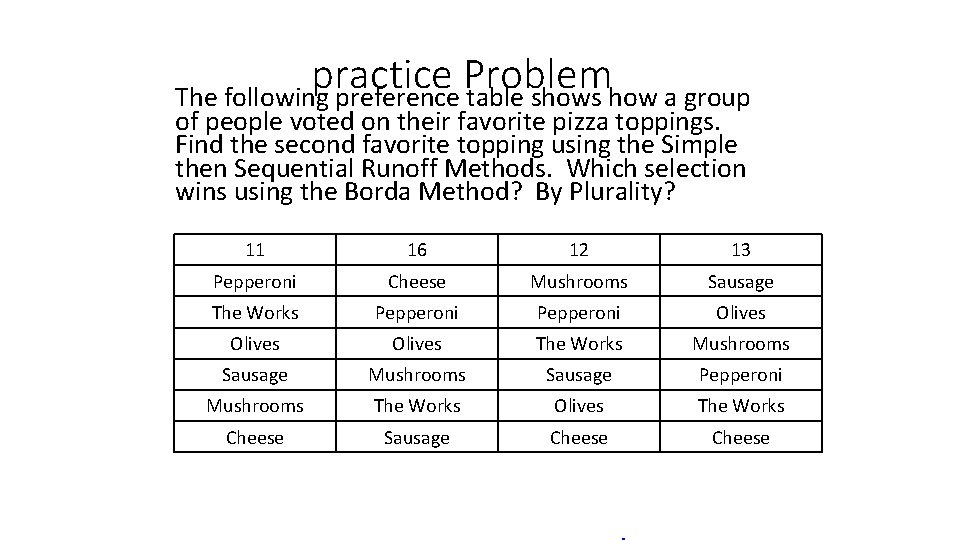
practice Problem The following preference table shows how a group of people voted on their favorite pizza toppings. Find the second favorite topping using the Simple then Sequential Runoff Methods. Which selection wins using the Borda Method? By Plurality? 11 16 12 13 Pepperoni Cheese Mushrooms Sausage The Works Pepperoni Olives The Works Mushrooms Sausage Pepperoni Mushrooms The Works Olives The Works Cheese Sausage Cheese

Warm-Up Problem Who wins this election using the Plurality, Simple Runoff and the Sequential Runoff Methods? Who wins using the Borda method? Jimmy Johns Subway Firehouse Jersey Mikes 26 Subway Firehouse Jersey Jimmy Mikes Johns Firehouse Subway Jimmy Johns 29 Jersey Mikes 31 Jimmy Johns Jersey Mikes Subway Firehouse Jimmy Johns 33 27 Subway

Marquis de Condorcet A French mathematician and philosopher proposed what is now called the Condorcet Method: • A Condorcet method is a voting system that will always elect the Condorcet winner; this is the candidate whom voters prefer to each other candidate, when compared to them one at a time. • This candidate can be found by conducting a series of pairwise comparisons (I call them battles), using the basic procedure described next.

Pairwise? Pairwise comparison generally refers to any process of comparing entities in pairs to judge which of each entity is preferred, • The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social choice, and public choice.

• https: //www. youtube. com/watch? v=i. P 8 g. Fswlr. SQ

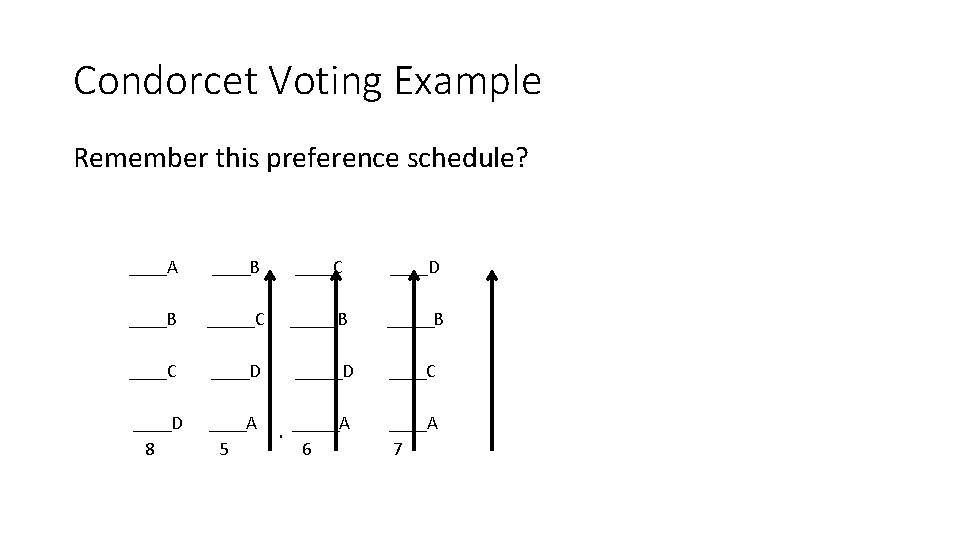
Condorcet Voting Example Remember this preference schedule? ____A ____B ____C ____D ____B _____C _____B ____C ____D ____C ____D ____A _____A 8 5 6 7

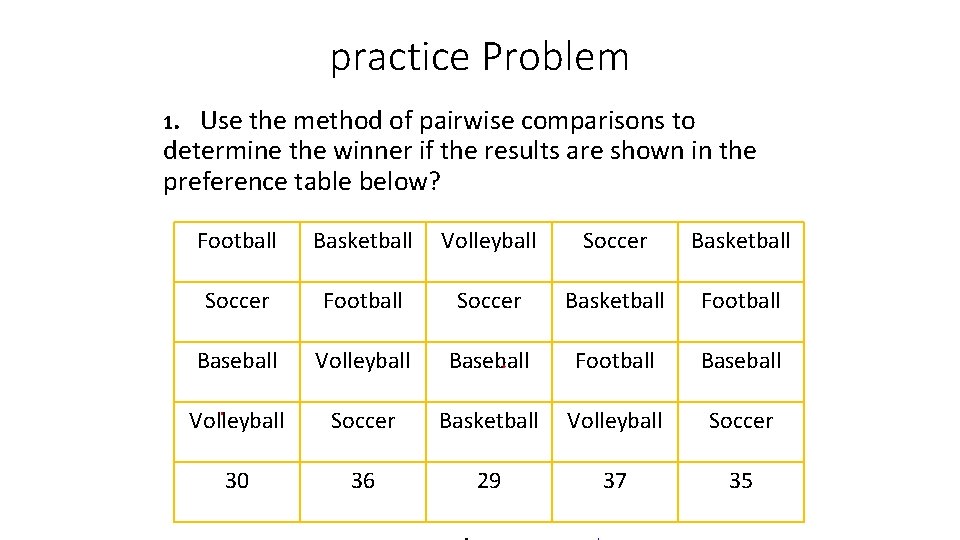
practice Problem 1. Use the method of pairwise comparisons to determine the winner if the results are shown in the preference table below? Football Basketball Volleyball Soccer Basketball Soccer Football Soccer Basketball Football Baseball Volleyball Baseball Football Baseball Volleyball Soccer Basketball Volleyball Soccer 30 36 29 37 35

A Way to Keep Track Football Basketball Soccer Volleyball Baseball

Pairwise Comparison Steps • To determine a “pairwise comparison” winner, compare each choice with each other choice…. . • Compare A with B, A with C, and then D and so on… • Assign 1 point for each pairwise comparison “win” and zero points for a loss and one-half point for a tie for each choice • Add up all the points after performing all of the possible pairwise comparisons to determine the Winner • If the winner wins or at least ties all of their “battles” then, he/she/it is considered to be a Condorcet winner.

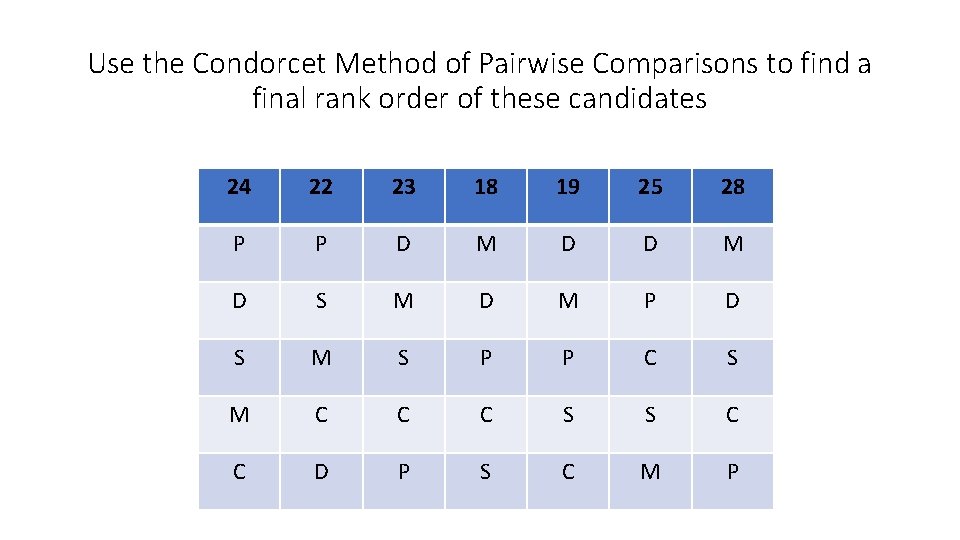
Use the Condorcet Method of Pairwise Comparisons to find a final rank order of these candidates 24 22 23 18 19 25 28 P P D M D S M D M P D S M S P P C S M C C C S S C C D P S C M P

Condorcet Voting • In a Condorcet election the voter ranks the list of candidates in order of preference. • In this respect it is the same as an election held under non-Condorcet methods such as instant runoff voting or the single transferable vote. • Some Condorcet methods allow voters to rank more than one candidate equally, so that, for example, the voter might express two first preferences rather than just one.

Condorcet Voting continued • Usually, when a voter does not give a full list of preferences then it is assumed, for the purpose of the count, to prefer the candidates he has ranked over all other candidates. Some Condorcet elections permit write-in candidates but, because this can be difficult to implement it is not often permitted.

Condorcet continued • In certain circumstances an election has no Condorcet winner. This occurs as a result of a kind of tie known as a majority rule cycle, described by CONDORCET’S PARADOX. The manner in which a winner is then chosen varies from one Condorcet method to another. • It is important to note that not all single winner, ranked voting systems are Condorcet methods. For example, instant-runoff voting and the Borda count do not satisfy the Condorcet criterion

practice Activity Use the Condorcet Method of Pairwise Comparison to find the winner of the election using these preference schedules A___ B___ C___ A __ C___ A ___ B __ 20 20

Continued • You should have noticed that, in the practice example, the Condorcet method produced contradictory results • This contradiction produces what is called a “paradox”…. . in this case the “Condorcet Paradox”

Project Expectations • Someone from your group must make an appointment during your class period (or during a teacher’s class period where you are enrolled) beginning on Monday. • You must be PREPARED! You must have a well-designed survey/set of directions. • You must write the options on the board for the students you are surveying. • You must be prepared to provide ballot paper. • You must act like a you professional adult. Explain why you are there and act like it means something important to you and the students will take it more seriously.

Election Theory Project • Design and submit a preference ballot with three or four “candidates” to ME for election using a Preference Ballot • Conduct your “election” of no less than 100 of your peers once the slate is approved by ME asking your “voters” to rank order their preferences • Collate your results and create a Preference Table to summarize your results using to report to the class • Using the Plurality and Borda Methods, analyze your results and summarize the election results for the report to the class. • Follow this by applying the Instant and Sequential Runoff Methods to your original results and analyze these results in your report at well.

Election Theory Project (continued) • Finally, complete the Pairwise Comparison method defined by Condorcet and determine the winner based on your results. • Each member of your group must participate and take part in a presentation. Presenters should be able to demonstrate a knowledge of procedures used to collect “votes”, create a “poster” or a “technology-based” presentation for the results, explain the instant and sequential runoff methods used, and conduct a mathematical analysis of these results. If you choose to create a technology-based presentation, you must accompany that with a visual hard-copy display of your survey and the results. • Lastly, each group should work together cooperatively and be helpful to each other in preparing for the final presentation. You will receive a quiz score for this project.

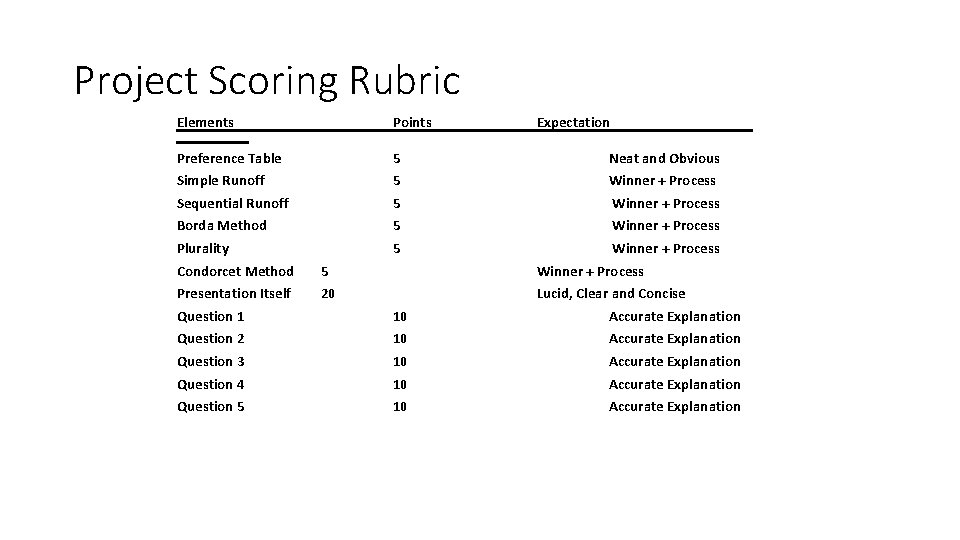
Project Scoring Rubric Elements Points Expectation Preference Table 5 Neat and Obvious Simple Runoff 5 Winner + Process Sequential Runoff 5 Winner + Process Borda Method 5 Winner + Process Plurality 5 Winner + Process Condorcet Method 5 Winner + Process Presentation Itself 20 Lucid, Clear and Concise Question 1 10 Accurate Explanation Question 2 10 Accurate Explanation Question 3 10 Accurate Explanation Question 4 10 Accurate Explanation Question 5 10 Accurate Explanation