Discrete Mathematics Counting and Its Applications 2016 Counting

이산수학(Discrete Mathematics) 계수와 응용 (Counting and Its Applications) 2016년 봄학기 강원대학교 컴퓨터과학전공 문양세

강의 내용 Counting and Its Applications 계수의 기본 원리(Basics of Counting) 비둘기 집 원리(The Pigeonhole Principle) 순열과 조합(Permutations and Combinations) Page 2 Discrete Mathematics by Yang-Sae Moon

Combinatorics (계수) Basics of Counting The study of the number of ways to put things together into various combinations. (주어진 물건을 여러 가지 조합으로 묶는 여러 가지 방법에 대한 연구이다. ) E. g. In a contest entered by 100 people, how many different top-10 outcomes could occur? (100명이 참여한 경연에서 톱 10이 구성되는 모든 경우의 수는? ) E. g. If a password is 6 -8 letters and/or digits, how many passwords can there be? (패스워드가 6 -8개의 글자/숫자로 구성된다면, 가능한 패스워드의 개수는? ) Page 3 Discrete Mathematics by Yang-Sae Moon

Sum and Product Rules Basics of Counting Let m be the number of ways to do task 1 and n the number of ways to do task 2 (with each number independent of how the other task is done), and assume that no way to do task 1 simultaneously also accomplishes task 2. (타스크 1을 수행하는데 m개, 타스크 2를 수행하는데 n개의 방법이 있다 하자(이때, 두 타 스크는 독립적이다). 또한, 두 개의 타스크는 동시에 수행될 수 없다고 가정하자. ) • The sum rule: The task “do either task 1 or task 2, but not both” can be done in m+n ways. (덧셈 법칙: 둘 중 하나만 수행하는 경우) [예: 주사위 혹은 동전 던지기] • The product rule: The task “do both task 1 and task 2” can be done in mn ways. (곱셈 법칙: 두 타스크를 모두 수행해야 하는 경우) [예: 주사위 던지고 동전도 던지기] Page 4 Discrete Mathematics by Yang-Sae Moon

Set Theoretic Version (집합 이론적 해석) Basics of Counting If A is the set of ways to do task 1, and B the set of ways to do task 2, and if A and B are disjoint, then: (A는 타스크 1을 수행하는 방법의 집합이고, B는 타스크 2를 수행하는 방법의 집 합이며, A와 B는 서로 소라 하자. 그러면, 다음이 성립한다. ) • The ways to do either task 1 or 2 are A B, and |A B|=|A|+|B| (타스크 1과 2중 하나를 수행하는 경우의 수는 합집합으로 해석된다. ) • The ways to do both task 1 and 2 can be represented as A B, and |A B|=|A|·|B| (타스크 1과 2 모두를 수행하는 경우의 수는 카티젼 곱으로 해석된다. ) Page 5 Discrete Mathematics by Yang-Sae Moon

Examples of Product Rules (4/4) Basics of Counting 예제(가능한 전화번호 개수): 전화번호가 NYX-NNX-XXXX의 체계를 가지고, N, Y, X는 각각 N=2~9, Y=0/1, X=0~9의 범위를 가질 때 가능한 전화번호의 개수는? • NYX: 8 x 2 x 10 = 160개 (예: 지역번호) • NNX: 8 x 10 = 640개 (예: 국번호) • XXXX: 10 x 10 = 10, 000개 • 결국, 160 x 640 x 10, 000 = 1, 024, 000개의 전화번호가 가능하다. Page 9 Discrete Mathematics by Yang-Sae Moon

IP Address Example (1/2) Basics of Counting Some facts about Internet Protocol version 4(IPv 4): • Valid computer addresses are in one of 3 types: − A class A IP address contains a 7 -bit “netid” ≠ 17, and a 24 -bit hostid” (클래스 A는 netid로 7 bits를 사용하나, 1111111은 사용치 않는다. ) − A class B address has a 14 -bit netid and a 16 -bit hostid. (클래스 B는 netid로 14 bits를 사용하고, 16 bits는 hostid로 사용한다. ) − A class C address has 21 -bit netid an 8 -bit hostid. (클래스 C는 netid로 21 bits를 사용하고, 8 bits는 hostid로 사용한다. ) • The 3 classes have distinct headers (0, 110). • Hostids that are all 0 s or all 1 s are not allowed. (모두 0이나 1일 수는 없다. 즉, “ 0. 0”이나 “ 255”는 제외한다. ) How many valid computer addresses are there? Page 13 Discrete Mathematics by Yang-Sae Moon

IP Address Example (2/2) Basics of Counting (# addresses) = (# class A) + (# class B) + (# class C) 덧셈 법칙 # class A = (# valid netids) x (# valid hostids) 곱셈 법칙 • (# valid class A netids) = 27 − 1 = 127. • (# valid class A hostids) = 224 − 2 = 16, 777, 214. Continuing in this fashion we find the answer is: 3, 737, 091, 842 (3. 7 billion IP addresses) However, the space will be insufficient! IPv 6 (256 bits) Page 14 Discrete Mathematics by Yang-Sae Moon

Inclusion-Exclusion Principle (포함 배제 원리) Basics of Counting Suppose that k m of the ways of doing task 1 also simultaneously accomplish task 2. (타스크 1을 수행하는 동시에 타스크 2를 수행할 수 있는 경우, 즉, 두 타스크가 동시에 수행될 수 있는 경우) Then the number of ways to accomplish “Do either task 1 or task 2” is m n k. (1 혹은 2를 수행하는 경우의 수는, 둘 중 하나를 수행하는 경우의 수에서 둘 다 수행하는 경우의 수를 뺀 값이다. ) Set theory: If A and B are NOT disjoint, then |A B|=|A| |B| |A B|. Page 15 Discrete Mathematics by Yang-Sae Moon

강의 내용 Counting and Its Applications 계수의 기본 원리(Basics of Counting) 비둘기 집 원리(The Pigeonhole Principle) 순열과 조합(Permutations and Combinations) Page 16 Discrete Mathematics by Yang-Sae Moon

Pigeonhole Principle (비둘기 집 원리) The Pigeonhole Principle A. k. a. (as known as) Dirichlet drawer principle (또한, “디리크레의 서랍 원리”라고도 알려짐) If ≥k+1 objects are assigned to k places, then at least 1 place must be assigned ≥ 2 objects. (k+1개의 객체(비둘기)가 k개의 장소(상자, 비둘기 집)에 배분된다면, 적어도 한 곳은 두 개 이상의 객체가 배분된다. ) In terms of the assignment function: If f: A→B and |A|≥|B|+1, then some element of B has ≥ 2 preimages under f. That is, f is not one-to-one. Page 17 Discrete Mathematics by Yang-Sae Moon

Examples of Pigeonhole Principle (3/3) The Pigeonhole Principle Let n = 3. Consider 1, 111, 1111. • 1%3=1 • 11 % 3 = 2 • 111 % 3 = 0 • 1, 111 % 3 = 1 1, 111 – 1 = 1, 110 = 370 x 3 • It has only 0’s and 1’s in its expansion. • 1, 110 mod 3 = 0, so it’s a multiple of 3. Page 20 Discrete Mathematics by Yang-Sae Moon

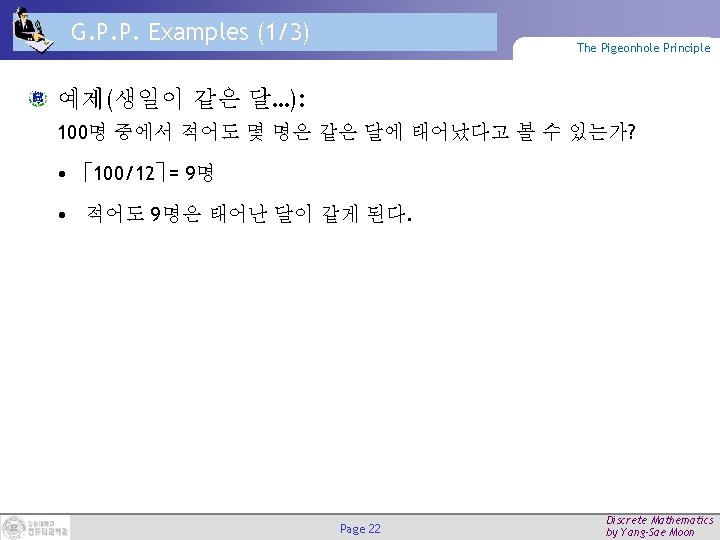
Generalized Pigeonhole Principle (G. P. P. ) The Pigeonhole Principle If N objects are assigned to k places, then at least one place must be assigned at least N/k objects. (N개의 객체가 k개 장소에 배정된다면, 적어도 한 곳은 N/k 개 객체를 가진다. ) E. g. , there are N=280 students in this class. There are k=52 weeks in the year. (학생 280명) (한 해는 52주) • Therefore, there must be at least 1 week during which at least 280/52 = 5. 38 =6 students in the class have a birthday. • (일반화된 비둘기 집 원리에 의해서) 최소 6명의 학생은 같은 주에 생일이 들어 있게 된다. Page 21 Discrete Mathematics by Yang-Sae Moon

강의 내용 Counting and Its Applications 계수의 기본 원리(Basics of Counting) 비둘기 집 원리(The Pigeonhole Principle) 순열과 조합(Permutations and Combinations) Page 25 Discrete Mathematics by Yang-Sae Moon

Permutations (순열) Permutations & Combinations A permutation of a set S of objects is a sequence containing each object once. (객체들의 집합 S에 대한 순열이란 해당 객체들이 한번씩 나오는(객체들을 한번 씩 포함하는) 시퀀스를 의미한다. ) An ordered arrangement of r distinct elements of S is called an r-permutation. (집합 S에 포함된 r개의 원소들을 순서대로 나열하는 방법을 r-순열이라 한다. ) The number of r-permutations of a set with n=|S| elements is (n개 중 r개를 선택하여 나열하는 방법은) Page 26 Discrete Mathematics by Yang-Sae Moon

Combinations (조합) (1/2) Permutations & Combinations An r-combination of elements of a set S is simply a subset T S with r members, |T|=r. (집합 S의 r-조합이란, r개의 원소를 가지는 S의 부분집합 T의 개수이다. ) (집합 S에서 r개의 원소(순서 무관)를 선택하는 방법의 개수이다. ) The number of r-combinations of a set with n=|S| elements is (n개 원소를 갖는 집합 S에 대한 r-조합의 개수는) Page 29 Discrete Mathematics by Yang-Sae Moon

Combinations (조합) (2/2) Permutations & Combinations Note that C(n, r) = C(n, n−r) • Because choosing the r members of T is the same thing as choosing the n−r non-members of T. • T에서 r개의 member를 선택하는 방법은 T에서 (n-r)개의 non-member를 선 택하는 방법과 동일하다. Page 30 Discrete Mathematics by Yang-Sae Moon

강의 내용 Counting and Its Applications 계수의 기본 원리(Basics of Counting) 비둘기 집 원리(The Pigeonhole Principle) 순열과 조합(Permutations and Combinations) Page 33 Discrete Mathematics by Yang-Sae Moon

Homework #6 Counting and Its Applications Homework #6 & Programming Assignment #2 Page 34 Discrete Mathematics by Yang-Sae Moon