Discrete Mathematics Chapter 4 Induction and Recursion By

Discrete Mathematics Chapter 4 Induction and Recursion By courtesy of Prof. Cheng-Chia Chen

Discrete Mathematics Ch 4 Contents 4. 1 4. 2 4. 3 4. 4 4. 5 Mathematical inductions Strong Induction and well-ordering Recursive definitions & structural induction Recursive algorithms Program correctness (skip) Transparency No. 4 -2

Discrete Mathematics Ch 4 4. 1 Mathematical Induction (MI) · Principle of MI: To show that a property p hold for all nonnegative integer n, it suffices to show that 1. Basis step: P(0) is true 2. Inductive step: P(n) P(n+1) is true for all nonnegative integer n. �P(n) in Step 2 is called the inductive hypothesis. Notes: 1. Math. Ind. is exactly the inference rule: �P(0), "n P(n) P(n+1) �----------------� "n P(n) for any property P 2. If the intended domain is all positive integers, then the basis step should be changed to: 1. Basis step: P(1) is true. Transparency No. 4 -3

Discrete Mathematics Ch 4 Examples 1. Show that for all positive integers n, 1 + 2 + … + n = n (n+1) /2. Pf: Let P(n) denote the proposition: 1 + 2 + … + n = n (n+1) /2. The proof is by induction on n. Basis step: P(1) is true since 1 = 1 x (1+1) /2. Ind. step: Assume p(k) holds for arbitrary integer k > 0, i. e. , 1 + 2 + … + k = k(k+1)/2. Then 1 + … + k + (k+1) = k(k+1)/2 + 2(k+1)/2 = (k+1)[(k+1)+1] /2. Hence p(k+1) is also true. This completes the proof of basis step and inductive step of MI, and hence by MI, p(n) holds for all positive integers n. Transparency No. 4 -4

Discrete Mathematics Ch 4 Examples : 2. Si=1, n 2 i-1 = n 2 3. n < 2 n 4. 3 | n 3 - n if n > 0 5. Si=1, n 2 i = 2(n+1) -1 6. Sj=1, n arj = arn+1 - a / (r - 1) 7. Let Hk = 1 + 1/2 +. . . + 1/k => H 2 n 1 + n/2 8. |S| = n => |2 S| = 2 n. 9. If n > 3 => 2 n < n! 10. ~(S 1Ç. . . ÇSn) = ~S 1 U. . . U ~Sn. 11. Odd Pie Fights 12. Checkerboard Tiling by Triominoes Transparency No. 4 -5

Discrete Mathematics Ch 4 7. Let Hk = 1 + 1/2 +. . . + 1/k. Then H 2 n 1 + n/2 for all non-negative integers n. Pf: By induction on n. Let p(n) be the proposition H 2 n 1 + n/2 Basis Step: n = 0. Then H 20 = H 1 = 1 1 + 0/2. Hence p(0) is true. Ind. Step: Assume p(n) holds for any n 0, i. e. , H 2 n 1 + n/2 holds for any n 0. Then H 2 n+1 = 1 +… + 1/2 n + 1/(2 n+1) + … 1/(2 n+2 n) H 2 n + 2 n x 1/(2 n+2 n) 1 + n/2 + ½ = 1 + (n+1)/2. This establishes the ind. step of MI. As a result p(n), i. e. , H 2 n 1 + n/2 , holds for all nonnegative integers n. Transparency No. 4 -6

Discrete Mathematics Ch 4 More examples: For every k 12, there are m, n 0 s. t. k = 4 m + 5 n. Pf: By induction on k’ where k’ = k-12. Basis: k’= 0 (i. e. , k = K'+12). Then k = 12 = 4 x 3 + 5 x 0. Inductive step: k’ = t’ + 1 > 0 (i. e. , k = t +1 > 12 ) By Ind. Hyp. , t = 4 m + 5 n. Then k = t + 1 = 4 m + 5 n + 1. If m > 0 => k = 4(m-1) + 5(n+1). If m = 0 => t = 5 n > 11 => n 3. Hence t+1 = 5(n-3) + 15 + 1 = 4 x 4 + 5(n-3). Q. E. D. Transparency No. 4 -7

Discrete Mathematics Ch 4 Correctness of MI · Correctness of MI: Let p(. ) be a property about positive integers. If p(1) holds and p(n) implies p(n+1) for all n, then it is true that p(n) holds for all positive integer n. Pf: Assume MI is incorrect. i. e. the set NP = {k > 0 | p(k) is false} is not empty. Let m be the least number of NP -- existence implied by well-ordering theorem Since p(1), 1 Ï NP and m > 1. => m-1 > 0 is a positive integer and p(m-1) is true => p(m) holds [by the inductive step of MI] => m Ï NP => a contradiction. Q. E. D. Transparency No. 4 -8

Discrete Mathematics Ch 4 Strong Induction and Well-Orering · [A problem MI is hard to prove. ] If n is a positive number > 1, then n can be written as a product of primes. · To prove this theorem using induction, we needs a stronger form of MI. Transparency No. 4 -9

Discrete Mathematics Ch 4 Strong Induction · [The 2 nd form of MI (Strong Induction; complete Induction)] To prove that p(n) holds for all non-negative integers n, where p(n) is a propositional function of n, it suffices to show that �Basis step: P(0) holds �Inductive step: P(0) / P(1) / , . . . , / p(k-1) P(k) holds for all k 0. �I. e. , assume P(0), …, P(k-1) hold for arbitrary k, and then show that p(k) is true as well. Notes: �P(0) / P(1) /. . . , / p(k-1) (or "t t<k P(k)) is called the induction hypothesis of the proof. �If our intended domain is positive integers, then the basis step is: P(1) holds, and Ind. Hyp. is P(1) /. . . , / P(k-1) Transparency No. 4 -10

Discrete Mathematics Ch 4 Example Ex 2: If n is a positive number > 1, then n can be written as a product of primes. Pf: Let p(n) be the proposition: if n > 1 then it can be written as a product of primes. Basis step: p(1) holds since ~ (n > 1). Ind. step: Let k be arbitrary positive number and assume p(t) holds for all t < k. There are two cases to consider: Case 1: k is a prime number, and then p(k) holds since k = k is the product of itself. Case 2: k is a composite number. Then by definition, there are two numbers 1 < a, b < k such that k = ab. By ind. hyp. , p(a) and p(b) hold and since a, b > 1, a and b can be written as a product of primes. Let a = a 1, …, ai and b = b 1, …bj, then k = a 1…ai x b 1…bj is a product of primes. Transparency No. 4 -11

Discrete Mathematics Ch 4 Correctness of Strong Induction and Well-ordering · Correctness of SI: Let p(. ) be a property about positive integers. If p(1) holds and p(1) / p(2) … / p(n) implies p(n+1) for all n, then it is true that p(n) holds for all n. Pf: Assume SI is incorrect, i. e. the set NP = {k | p(k) is false} is not empty. Let m be the least number of NP -- existence by well-ordering property of positive integers Since p(1), 1 Ï NP and m >1. => m-1 exists and for all t < m, p(t) is true => p(m) holds [by the inductive step of SI] => m Ï NP => a contradiction. Q. E. D. · Ex. Match Removal · Ex. Triangulation of Simple Polygons Transparency No. 4 -12

Discrete Mathematics Ch 4 Well-ordered Property · [Well-ordered property of natural numbers] Every non-empty subset of non-negative integers has a least element. (每一非空自然數子集合必然存在最小 元素。) · The property can be used directly in the proof (in place of MI or SI). Ex: In round-robin tournament, every player plays every other exactly once and each match has a winner and a looser. We say p 1, p 2, …, pm form a cycle of length m if p 1 beats p 2, p 2 beats p 3, …, pm beats p 1. Show that if there is a cycle of length m 3, then there must exist a cycle of 3. Transparency No. 4 -13

Discrete Mathematics Ch 4 Ex. 6 Pf: Let C be the set {n | there is a cycle of length n} in the tournament. Obviously, m C and C is a subset of non-negative integers. So by well-ordering property, C has a least element, say k. Let p 1, p 2, …, pk be such cycle. Since there is no cycle of 1 or 2, k must 3. If k = 3, then we are done. O/w, k > 3 and consider p 1 and p 3. If p 3 beats p 1, then p 1, p 2, p 3 is a cycle of length 3 < k, a contradiction. If p 1 beats p 3, then p 1, p 3, …, pk form a cycle of length < k. This violates the fact that k is the least element of C. As a result, k must = 3. Transparency No. 4 -14

Discrete Mathematics Ch 4 4. 3 Recursive definitions and structural induction · Different ways of defining a functions �Explicit listing Ø Suitable for finite functions only. �Define by giving an explicit expression ØEx: F(n) = 2 n �Recursive (or inductive) definition ØDefine value of objects (sequences, functions, sets, . . . ) in terms of values of smaller similar ones. ØEx: the sequence 1, 2, 4, . . . (an = 2 n) can be defined recursively as follows: 1. a 0 = 1; 2. an+1 = 2 x an for n > 0. Transparency No. 4 -15

Discrete Mathematics Ch 4 Recursively defined functions · To define a function f with the set of nonnegative integers as its domain: �Specify the value of f at 0 (i. e. , f(0)) �Given a rule for finding f(n) from f(n-1), . . . , f(0). Ø i. e. , f(n) = some expression in terms of n and f(n), . . . , f(0). �Such a definition is called a recursive or inductive definition. · Ex 1: �f(n) = 3 if n = 0 � = 2 f(n-1) +3 if n > 0 �=> f(0) = 3, f(1) = 2 f(0) +3 = 9; f(2) = 2 f(1)+3 = 21, . . . �This guarantees that f is defined for all numbers. Transparency No. 4 -16

Discrete Mathematics Ch 4 More examples functions · Ex 2: The factorial function f(n) = n! �f(0) = 1 �f(n) = n f(n-1) for all n > 0. · Recursively defined functions (over N) are well defined. Pf: Let P(n) = "there is at least one value assigned to f(n)". Q(n) = "there at most one value assigned to f(n)". We show P(n) holds for all n by MI. Basis: P(0) holds. Ind. : Assume p(k) holds for all k ≤ n. => Since f(n+1) can be assigned a value by evaluating the expr(n, f(0), . . , f(n)), where by ind. hyp. all f(i)s (i<n) have been assigned a value. The fact that Q(n) holds for all n is trivial, since each f(k) appears at the left hand side of the definition exactly once. QED Transparency No. 4 -17

Discrete Mathematics Ch 4 More examples: Ex 5: The Fibonacci sequence: �f(0) = 0; f(1) = 1; �f(n) = f(n-1) + f(n-2) for n > 1. �==> 0, 1, 1, 2, 3, 5, 8, … Transparency No. 4 -18

Discrete Mathematics Ch 4 Ex 6: Show that f(n) > a n-2 whenever n ≥ 3, where a = (1+ sqrt(5))/2 = 1. 618 is the golden ratio · Properties of a: a 2 = (1 + a). Pf: (by MI) Let P(n) = "f(n) > a n-2 ". Basis: P(3) holds since f(3) = 2 > a 3 -2. Ind. Step: (for n ≥ 4) If n = 4 => f(4) = 3 > a 4 -2 = 1. 6182. If n > 4 => by ind. hyp. , f(n-1) >an-3, f(n-2) >an-4 Hence f(n) = f(n-1) + f(n-2) > an-3 + an-4 = (1+ a) an-4 = an-2. QED (Supplementary material) Transparency No. 4 -19

Discrete Mathematics Ch 4 Lame's theorem (skip) · a, b: positive integer with a b. => #divisions used by the Euclidean algorithm to find gcd(a, b) £ 5 x #decimal digits in b. Pf: seq of equations used for finding gcd(a, b) where r 0 = a, r 1 = b. r 2 = ro mod r 1 ¹ 0, r 3 = r 1 mod r 2 ¹ 0. . . … rn = rn-2 mod rn-1 ¹ 0, rn+1 = rn-1 mod rn = 0 i. e. , until rn | rn-1. Then gcd(a, b) = rn. and #division used = n. Note: rn 1 = f 2 ; rn-1 2 rn 2 f 2 = f 3; rn-2 rn+rn-1 = f 2 + f 3 = f 4. . . (被除數 除術+餘數) r 2 r 3 + r 4 fn-1+fn-2=fn; b = r 1 r 2+ r 3 fn+fn-1 = fn+1. > an-1. logb > (n-1) log a ~ 0. 208 (n-1) > (n-1)/5 n -1 < 5 log b < 5 #digit(b). => n £ 5#digit(b). Transparency No. 4 -20

Discrete Mathematics Ch 4 Recursively defined sets · Given a universal set U, a subset V of U and a set of operations OP on U, we often define a subset D of U as follows: � 1. Init. (Basis Step): Every element of V is an element of D. � 2. Closure (Recursive Step): For each operation f in OP, if f: Un->U and t 1, . . , tn are objects already known to be in the set D, then f(t 1, . . , tn) is also an object of D. · Example: The set S = {3 n | n >0} can be defined recursively as follows: � 1. Init: 3 ∈ S (i. e. , V = {3}) � 2. Closure: S is closed under +. � i. e. , If a, b ∈ S then so is a+b. (OP = {+}) �(Can be proven by MI. ) Transparency No. 4 -21

Discrete Mathematics Ch 4 Well-formed arithmetic expressions (skip) Ex 11 : (2 +x), (x + (y/3)), . . . (ok) x 2+, xy*/3. . . (no) Let Vr = {x, y, . . , } be the set of variables, M = numerals = finite representations of numbers OP = {+, -, x, /, ^} U = the set of all finite strings over Vr U M U OP U {(, )}. The set of all well-formed arithmetic expressions (wfe) can be defined inductively as follows: 1. Init: every variable x in Vr and every numeral n in M is a wfe. 2. closure: If A, B are wfe, then so are (A+B), (A-B), (A * B), (A / B) and (A ^ B). Note: "1 + x " is not a wfe. Why ? (1+x) Transparency No. 4 -22

Discrete Mathematics Ch 4 More examples: (skip) · Ex 10: wff (well-formed propositional formulas) �PV: {p 1, p 2, . . } a set of propositional symbols. �OP = {/, /, ~, -> } �U = the set of all finite strings over PV U OP U {(, )} �Init: every pi ∈ PV is a wff �closure: If A and B are wffs, then so are � (A/B), (A /B), (A->B), (A <->B), and ~A. Transparency No. 4 -23

Discrete Mathematics Ch 4 Notes about recursively defined sets (skip) 1. The definition of D is not complete (in the sense that there are multiple subsets of U satisfying both conditions). Ex: the universe U satisfies (1) and (2), but it is not Our intended D. 2. In fact the intended defined set 3': D is the least of all subsets of U satisfying 1 & 2, or 3'': D is the intersection of all subsets of U satisfying 1 & 2 or 3''': Only objects obtained by a finite number of applications of rule 1 & 2 are elements of D. 3. It can be proven that 3', 3'', and 3''' are equivalent. 4. Hence, to be complete, one of 3', 3'' or 3''' should be appended to condition 1 & 2, though it can always be omitted (or replaced by the adv. inductively, recursively) with such understanding in mind. Transparency No. 4 -24

Discrete Mathematics Ch 4 Proof of the equivalence of 3', 3'' and 3''‘ (skip) · D 1: the set obtained by 1, 2, 3' � D 1 satisfies 1&2 and any S satisfies 1&2 is a superset of D 1. · D 2: the set obtained by 1, 2, 3''. � D 2 = the intersection of all subsets Sk of U satisfying 1&2. · D 3: the set obtained by 1, 2, 3'''. �For any x ∈ U, x ∈ D 3 iff there is a (proof) sequence x 1, . . . , xm = x, such that for each xi (i = 1. . m) either Ø (init: ) xi ∈ V or Ø (closure: ) there are f in OP and t 1, . . . tn in {x 1, . . , xi-1} s. t. Ø xi = f(t 1, . . , tn). Transparency No. 4 -25

Discrete Mathematics Ch 4 Proof (skip) 1. D 2 satisfies 1&21. 1 and is the least 1. 2 of all sets satisfying 1&2 , Hence D 1 exists and equals to D 2. 2 (2. 1) D 3 satisfies 1 & 2. (2. 2) D 3 is contained in all sets satisfying 1 & 2. Hence D 3 = D 2. pf: 1. 1: Let C = { T 1, …, Tm, …} be the collection of all sets satisfying 1&2, and D 2, by definition, is ∩C. Hence V Tk for all Tk ∈ C and as a result V D 2. --- (1) Suppose t 1, …, tn ∈ D 2, then t 1, …, tn ∈ Tk for each Tk in C, Hence f(t 1, …, tn) ∈ Tk and as a result f(t 1, . . , tn) ∈ D 2. ---(2). 1. 2: Since D 2 = ∩C, D 2 is a subset of all Tk’s, and by 1. 1, D 2∈C, D 2 thus is the least among these sets. Hence D 1 exists and equals to D 2. Transparency No. 4 -26

Discrete Mathematics Ch 4 2. 1 D 3 satisfies 1 & 2. [ by ind. ] (skip) 2. 2 D 3 is contained in all sets satisfying 1 & 2 [by ind. ] Hence D 3 = D 2. pf: 2. 1: two propositions need to be proved: V ⊆ D 3 ---(1) and {t 1, . . , tn}⊆ D 3 => f(t 1, …, tn) ∈ D 3 ---(2). (1) is easy to show, since for each x in V, the singleton sequence x is a proof. Hence x ∈ D 3. As to (2), since {t 1, . . , tn}⊆ D 3, by definition, there exist proof sequences S 1, S 2, …, Sn for t 1, …, tn, respectively. We can thus join them together to form a new sequence S = S 1, S 2, …, Sn. We can then safely append f(t 1, …, tn) to the end of S to form a new sequence for f(t 1, …, tn), since all t 1, …, tn have appeared in S. As a result f(t 1, …, tn) ∈ D 3. (2) thus is proved. Transparency No. 4 -27

Discrete Mathematics Ch 4 (skip) 2. 2 D 3 is contained in all sets satisfying 1 & 2 [by ind. ] pf: Let D be any set satisfying 1&2. We need to show that for all x, x ∈ D 3 =>x ∈ D. The proof is by ind. on the length m of the minimum proof sequence for x: x 1, …, xm = x If m = 1 then x=x 1 ∈ V, and hence x ∈ D. If m = k+1 > 1, then either xm ∈ V (and xm ∈ D) or ∃ j 1, j 2, …jn < m and xm = f(xj 1, …, xjn) for some f ∈ OP. For the latter case, by ind. hyp. , xj 1, …xjn ∈ D. Since D satisfies closure rule, f(xj 1, …, xjn) = xm ∈ D. Q. E. D Transparency No. 4 -28

Discrete Mathematics Ch 4 Example: Def 2: The set S*of strings over an alphabet S can be defined recursively as follows: �Basis Step: e ∈ S*. �Recursive Step: If a ∈ S and x ∈ S*, then ax ∈ S*. Ex 8': If S = {0, 1, 2}, then 1201 ∈ S* since �e 1 e = 1 01 201 1201. Ex 8'': The set of natural numbers can be defined as a subset of {1}* inductively as follows: �Init: e in N. �Closure: If x in N, then 1 x in N. e, 1, 111, 1111, . . . are natural numbers �(unary representation of natural numbers) Transparency No. 4 -29

Discrete Mathematics Ch 4 Induction principles III (structural induction) (skip) · D: a recursively defined set · P: D {true, false}; a property about objects of D. · To show that P(t) holds for all t ∈ D, it suffices to show that � 1. Basis Step: P(t) holds for all t ∈ V. � 2. Ind. Step: For each f in OP and t 1, . . , tn ∈ D, if P(t 1), . . . , P(tn) holds, then P(f(t 1, . . , tn)) holds, too. Transparency No. 4 -30

Discrete Mathematics Ch 4 Correctness of SI (skip) · Show the correctness of structural induction. Pf: Assume not correct. => NP = {t ∈ D | P(t) does not hold} is not empty. =>let x be any member of NP with a minimum length n of proof sequence, say x 1, . . xn = x. Since x has minimum length in NP, all x 1, . . xn-1 ∉ NP. => If n =1, then x 1 = x ∈ V (impossible) Else either n > 1 and x ∈ V (impossible, like n=1) or n > 1, and x=f(t 1, . , tn) for some {t 1, . . , tn} in {x 1, . . xn-1} and P holds for all tk’s => P(x) holds too => x ∉ NP, a contradiction. QED. Transparency No. 4 -31

Discrete Mathematics Ch 4 MI is a specialization of SI (skip) · Rephrase the SI to the domain N, we have: �To show P(t) holds for all t ∈ N, it suffices to show that �Init: P(e ) holds �Ind. step: [OP={ 1+ }] � for any x in N, If P(x) holds than P(1 x) holds. · Notes: � 1. The above is just MI. � 2. MI is only suitable for proving properties of natural numbers; whereas SI is suitable for proving properties of all recursively defined sets. � 3. The common variant of MI starting from a value c ≠ 0 , 1 is also a special case of SI with the domain �D = {c, c+1, c + 2, … } Transparency No. 4 -32

Discrete Mathematics Ch 4 Well-formed arithmetic expressions (skip) Ex 11 : (2 +x), (x + (y/3)), . . . (ok) x 2+, xy*/3. . . (no) Let Vr = {x, y, . . , } be the set of variables, M = numerals = finite representations of numbers OP = {+, -, x, /, ^} U = the set of all finite strings over Vr U M U OP U {(, )}. The set of all well-formed arithmetic expressions (wfe) can be defined inductively as follows: 1. Init: every variable x in Vr and every numeral n in M is a wfe. 2. closure: If A, B are wfe, then so are (A+B), (A-B), (A * B), (A / B) and (A ^ B). Note: "1 + x " is not a wfe. Why ? Transparency No. 4 -33

Discrete Mathematics Ch 4 More examples: (skip) · Ex 10: wff (well-formed propositional formulas) �PV: {p 1, p 2, . . } a set of propositional symbols. �OP = {/, /, ~, -> } �U = the set of all finite strings over PV U OP U {(, )} �Init: every pi ∈ PV is a wff �closure: If A and B are wffs, then so are � (A/B), (A /B), (A->B), (A <->B), and ~A. Transparency No. 4 -34

Discrete Mathematics Ch 4 (skip) · Ex 9: Recursively define two functions on S*. �len : S* -> N s. t. len(x) = the length of the string x. � Basis: len(e) = 0 � Ind. step: for any x ∈ S* and a ∈S, len(ax) = len(x) + 1. �+: S* x S* s. t. +(x, y) = x+y = the concatenation of x and y. �Basis: e + y = y for all strings y. �Recursive step: (az) + y = a(z+y) for all symbols a and strings z, y. Transparency No. 4 -35

Discrete Mathematics Ch 4 (skip) · Prove properties of len(-) on S*: Ex 14: show that len(x+y) = len(x)+len(y) for any x, y ∈ S*. �By SI on x. Let P(x) = "len(x+y) = len(x) +len(y)". � Basis: x = e. => � x + y => len(x + y) = len(e) + len(y). � Ind. step: x = az � len(x+y) = len((az) + y) = len((a(z+y)) � = 1 + len(z+y) � = 1+ len(z) + len(y) -- SI � = len(az) +len(y) � = len(x) + len(y). Transparency No. 4 -36

Discrete Mathematics Ch 4 Where do we use recursion? · Define a domain �numbers, lists, trees, formulas, strings, . . . · Define functions on recursively defined domains (n!) · Prove properties of functions or domains by structural induction. · Compute recursive functions �--> recursive algorithm Transparency No. 4 -37

Discrete Mathematics Ch 4 Define lp, rp : wff N (skip) · Define two functions lp, rp : wff N s. t. , � lp(A) and rp(A) are the number of '(' and ')' occurring in A, respectively. · Define lp and rp recursively by cases of input A: �Basis Case: A = p is a logical variable. � Then lp(A) = rp(A) = 0. �Recursive cases: � 1. A = (B @C ) where @ is either / or / or <->. � Then lp((B@C)) = 1 + lp(B) + lp(C) and � rp((B@C)) = 1 + rp(B) + rp(C). � 2. A= ~B. Then lp(~B) = lp(B) and rp(~B) = rp(B). · EX: lp( (p 1 / (~p 2 p 1)) ) = rp( (p 1 / (~p 2 p 1)) ) = 2. Transparency No. 4 -38

Discrete Mathematics Ch 4 (skip) Ex 13: Show that for every wff A, lp(A) = rp(A). Namely, every wff has an equal number of left and right parentheses. pf: By S. I. on A. Basis Step: A = p is a logic variable. Then lp(p) = 0 = rp(p). Recursive step: case 1: A= (B@C), where @is any binary connective. Then lp(A) = 1 + lp(B) + lp(C) --- Definition of lp = 1 + rp(B) + rp(C) --- Ind. Hyp. =rp(A) --- Def. of rp. case 2: A=~B. Then lp(A) = lp(B) = rp(A). Transparency No. 4 -39

Discrete Mathematics Ch 4 Full Binary Tree Def 6: The set of full binary trees can be defined inductively as follows: Basis Step: A single vertex is a full binary tree. Recursive Step: If T 1 and T 2 are disjoint full binary trees, and r is a vertex not in T 1 and T 2, then (r, T 1, T 2) is a full binary tree with root r, left subtree T 1 and right subtree T 2. Ex: r 0, (r 2, r 0, r 1), (r 3, r 0, (r 2, r 1, r 4)) Counter Ex: (r 0, r 1) Transparency No. 4 -40

Discrete Mathematics Ch 4 Internal nodes and leaves: Def: 1. A vetex r in a full binary tree T is an internal node if it has two subtrees. 2. A vetex r in a full binary tree T is a leaf if it has no subtrees. Def: Define two functions #Int, #leaf: the set of full binary tree N recursively as follows: Basis Case: t = r is a single node tree. Then #Int(r) = 0 and #leaf(r) = 1. Recursive Case: t = (r, T 1, T 2) is a non-single node tree. Then #Int(t) = 1 + #Int(T 1) + #Int(T 2) and #leaf(t) = #leaf(T 1) + #leaf(T 2). Transparency No. 4 -41

Discrete Mathematics Ch 4 Show that for all full binary trees T, the set of leaves is 1 more than the set of internal vertices. I. e. , #leaf(T) = 1 + #Int(T). Pf: By S. I. on T. Basis Case: T is a single-vertex tree. Then #leaf(T) = 1 + 0 = 1 + #Int(T). Ind. Case: T = (r, T 1, T 2). Then #leaf(T) = #leaf(T 1) + #leaf(T 2) --- Def of #leaf = 1 + #Int(T 1) + 1 + #Int(T 2) --- Ind. Hyp. = 1 + #Int( T ) --- Def. of #Int. Transparency No. 4 -42

Discrete Mathematics Ch 4 3. 4 Recursive algorithm · Definition: an algorithm is recursive if it solves a problem by reducing it to an instance of the same problem with smaller inputs. · Ex 1: compute an where a ∈ R and n ∈ N. · Ex 2: gcd(a, b) a, b ∈ N, a > b gcd(a, b) =def if b = 0 then a else gcd(b, a mod b). · Ex: show that gcd(a, b) will always terminate. · Comparison b/t recursion and iteration � Recursion: easy to read, understand devise. � Iteration: use much less computation time. � Result: programmer --> recursive program --> � compiler --> iterative program --> machine. � Exp: F(n+1) – 1 vs. n additions for calculating F(n) � Exp: O(n log n) for merge sort Transparency No. 4 -43

Discrete Mathematics Ch 4 3. 5 Program correctness (skip hereinafter) · After designing a program to solve a problem, how can we assure that the program always produce correct output? · Types of errors in a program: �syntax error easy to detect by the help of compilers �semantic error test or verify · Program testing can only increase our confidence about the correctness of a program; it can never guarantee that the program passing test always produce correct output. · A program is said to be correct if it produces the correct output for every possible input. · Correctness proof generally consists of two steps: �Termination proof : �Partial correctness: whenever the program terminates, it will produce the correct output. Transparency No. 4 -44

Discrete Mathematics Ch 4 Program verification · Problem: �what does it mean that a program produce the correct output (or results)? ØBy specifying assertions (or descriptions) about the expected outcome of the program. · Input to program verifications: �Pr : the program to be verified. �Q : final assertions (postconditions), giving the properties that the output of the program should have �P : initial assertions (preconditions) , giving the properties that the initial input values are required to have. Transparency No. 4 -45

Discrete Mathematics Ch 4 Hoare triple: · P, Q; assertions · S: a program or program segment. · P {S} Q is called a Hoare triple, meaning that S is partially correct (p. c. ) w. r. t P, Q, i. e. , whenever P is true for I/P value of S and terminates, then Q is true for the O/P values of S. Ex 1: x=1 {y : = 2; z : = x+ y} z = 3 is true. Why ? Ex 2: x = 1 { while x > 0 x++ } x = 0 is true. why? Transparency No. 4 -46

Discrete Mathematics Ch 4 Typical program constructs: 1. assignment: x : = expr �x : = x+y-3 2. composition: S 1; S 2 �Execute S 1 first, after termination, then execute S 2. 3. Conditional: � 3. 1 If <cond> then S � 3. 2 If <cond> then S 1 else S 2. 4. Loop: � 4. 1 while <cond> do S � 4. 2 repeat S until <cond> // 4. 3 do S while <cond> … · Other constructs possible, But it can be shown that any program can be converted into an equivalent one using only 1, 2, 3. 1 and 4. 1 Transparency No. 4 -47

Discrete Mathematics Ch 4 Assignment rule · P[x/expr] {x : = expr } P �P[x/expr] is the result of replacing every x in P by the expression expr. �ex: P = "y < x / x + z = 5" => P[x/3] = “y < 3 / 3+z = 5". �Why correct? �consider the variable spaces �(. . . , x, . . . ) == x : = expr ==> (. . . , expr, . . . ) |= P �Hence if P[x/expr] holds before execution, P will hold after execution. �Example: Q {y : = x+y} x > 2 y + 1 => Q = ? �(xb, yb) ==>{ya : = xb+yb} ==>(xb, xb+yb) = (xa, ya) |= P(xa, ya) =def ‘’xa > 2 ya +1’’ �=> (xb, yb) |= Q = P(xa, ya)[xa/xb; ya/xb+yb] � = P(xb, xb+yb) “xb > 2(xb+yb) +1” Transparency No. 4 -48

Discrete Mathematics Ch 4 Composition rules: · Splitting programs into subprograms and then show that each subprogram is correct. · The composition rule: P {S 1} Q x = 0 { x: = x+2} ? Q {S 2} R ? { x : = x-1} x > 0 ----------------------------P {S 1; S 2} R x=0 {x: = x+2; x: = x -1} x > 0 · Meaning: �Forward reading: �Backward reading: to prove P{S 1; S 2}Q, it suffices to find an assertion Q s. t. P{S 1}Q and Q {S 2}R. · Problem: How to find Q ? Transparency No. 4 -49

Discrete Mathematics Ch 4 Example: · Show that x =1 {y : = 2; z : = x +y} z = 3 · x = 1 {y : = 2; z : = x+y} z = 3 · ----------------------------· x=1 {y : = 2} ? ? {z : = x+y} z = 3 Transparency No. 4 -50

Discrete Mathematics Ch 4 Classical rules: P => P 1 {S} Q -----------P {S} Q 1 Q 1 => Q -----------P{S} Q P => P 1 {S} Q 1 => Q ------------P {S} Q Examples: x = 1 => x+1>1 x+1>0 {x : = x + 1} x > 0 x+1>1 { x : = x + 1 } x > 1 x > 0 => x ≠ 0 ------------------x = 1 { x : = x + 1} x > 1 x+1 > 0 {x : = x+1 } x ≠ 0 Transparency No. 4 -51

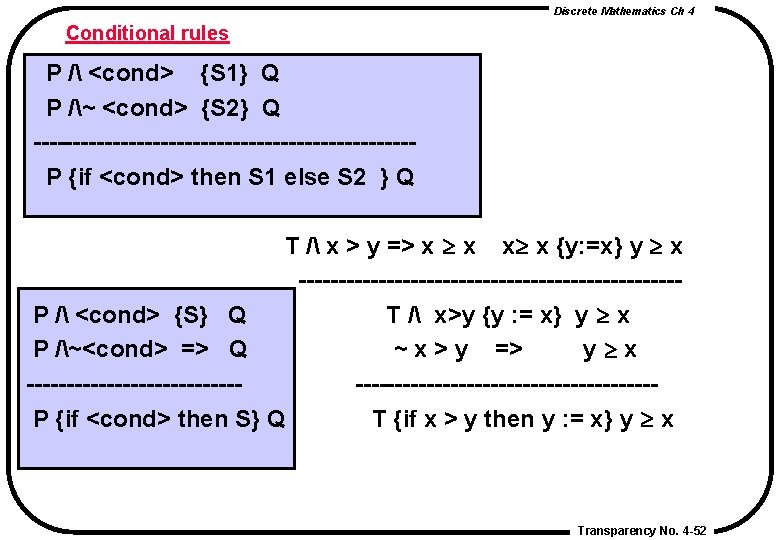
Discrete Mathematics Ch 4 Conditional rules P / <cond> {S 1} Q P /~ <cond> {S 2} Q ------------------------P {if <cond> then S 1 else S 2 } Q T / x > y => x x x x {y: =x} y x ------------------------P / <cond> {S} Q T / x>y {y : = x} y x P /~<cond> => Q ~ x > y => y x --------------------------------P {if <cond> then S} Q T {if x > y then y : = x} y x Transparency No. 4 -52

Discrete Mathematics Ch 4 While-loop rules · Loop invariant: � A statement P is said to be a loop invariant of a while program: While <cond> do S, if it remains true after each iteration of the loop body S. �I. e. , P / <cond> {S} P is true. · While rule: �P / <cond> {S} P �--------------------------�P {while <cond> do S} P / ~<cond> · Issues: �How to find loop invariant P? �Most difficulty of program verification lies in the finding of appropriate loop invariants. Transparency No. 4 -53

Discrete Mathematics Ch 4 While loop example Show that n>0 { i: = 1; f : = 1; while i < n do (i : = i+1 ; f : = f x i ) } f = n! To prove the program terminates with f = n!, a loop invariant is needed. Let p = "i ≤ n / f = i!" First show that p is a loop invariant of the while program i. e. , i £ n / f = i! / i < n { i: = i+1; f: = f x i} i£ n / f=i! Transparency No. 4 -54

Discrete Mathematics Ch 4 While loop example (cont'd) n > 0 --- i: = 1; ------ i ≤ n f : = 1; ------ p = "i ≤ n / f = i! “ while i < n do (i : = i+1 ; f : = f x i ) ------ p / ~ i < n ==> i=n / f = i! ==> f = n! Transparency No. 4 -55

Discrete Mathematics Ch 4 Another example: Ex 5: Show that the following program is correct: Procedure prod(m, n: integer) : integer 1. If n < 0 then a : = -n else a : = n ; ------ a = |n| 2. k : = 0 ; x : = 0 3. while k < a do --- p = "x = mk / k ≤ a" is a loop x : = x + m; invariant. k : = k+1 enddo --- x = mk / k ≤ a / ~k<a => k=a / x=ma => x = m |n| 4. If n < 0 then prod : = -x => prod = - m |n| = mn else prod : = x => Prod = m |n| = mn ---- prod = mn. Hence the program is [partially] correct ! Note: to be really correct, we need to show that the program will eventually terminates. Transparency No. 4 -56