Discrete mathematics Boolean Algebra and Logic Circuits Duality

Discrete mathematics Boolean Algebra and Logic Circuits. Duality N. V. Bilous Faculty of computer sciences Software department, KNURE, Software department, Ph. 7021 -446, e-mail: belous@kture. Kharkov. ua

Topic 1 Boolean Algebra and Logic Circuits ХНУРЭ, кафедра ПО ЭВМ, Тел. 7021 -446, e-mail: belous@kture. Kharkov. ua

Boolean Variables and Functions Let B = {0, 1}. The variable x is called a Boolean variable or a variable logic variable if it assumes values only from B. variable Values 0 and 1 Boolean variables is called Boolean constants 3

Boolean Variables and Functions A function y=f(x 1, x 2, . . . , xn) is called a Boolean function or a logic function if it assumes values function from B and each of its variables also assumes values from B. A Boolean function is called a Boolean function of degree n if its formula contains n different variables. 4

The conjunction L(x 1, x 2)= x 1 x 2 where L=1 if x 1=1 and x 2=1, L=0 otherwise. The “ ” symbol is called the conjunction or conjunction AND operator, operator and the circuit in Figure 1 is said to implement the conjunction. Figure 1 – The conjunction (series connection) 5

The disjunction L(x 1, x 2) = x 1 x 2 where L=1 if x 1=1 or x 2=1 or if x 1=x 2=1, L=0 if x 1=x 2=1. The symbol is called the disjunction or disjunction OR operator, operator and the circuit in Figure 2 is said to implement the disjunction. Figure 2 – The disjunction (parallel connection) 6

The negation L(x) = x where L=1 if x=0 L=0 if x=1. The value of this function is the inverse of the value of the input variable. Instead of using the word inverse, it is more common to use the term negation or negation complement 7

Methods of Boolean function representation I. Truth table The values of a Boolean function are often displayed in the form of a table called the truth table The rows amount in a truth table is equal to the amount of different interpretations of the function (2 n). 8

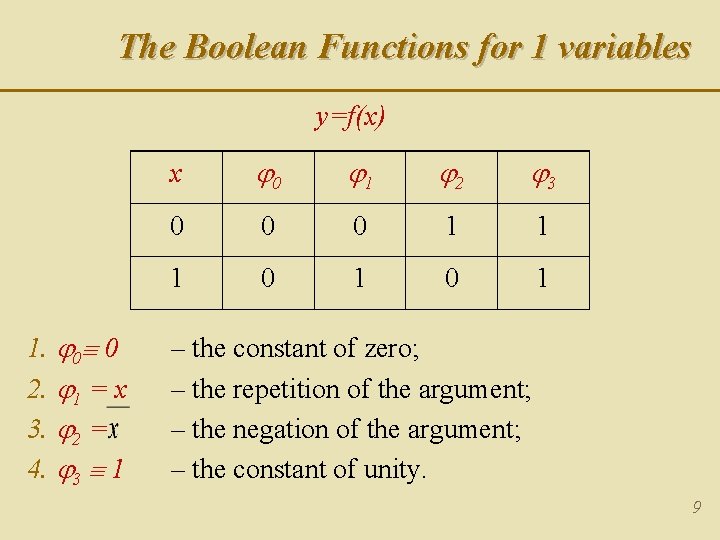
The Boolean Functions for 1 variables y=f(x) 1. 0 0 2. 1 = x 3. 2 = 4. 3 1 x 0 1 2 3 0 0 0 1 1 1 0 1 – the constant of zero; – the repetition of the argument; – the negation of the argument; – the constant of unity. 9

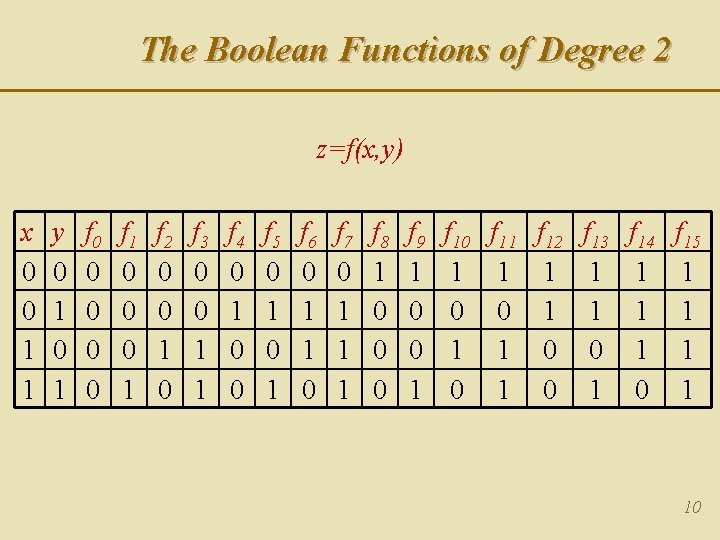
The Boolean Functions of Degree 2 z=f(x, y) x 0 0 1 1 y 0 1 f 0 0 0 f 1 0 0 0 1 f 2 0 0 1 0 f 3 0 0 1 1 f 4 0 1 0 0 f 5 0 1 f 6 0 1 1 0 f 7 0 1 1 1 f 8 1 0 0 0 f 9 1 0 0 1 f 10 1 0 f 11 1 0 1 1 f 12 1 1 0 0 f 13 1 1 0 1 f 14 1 1 1 0 f 15 1 1 10

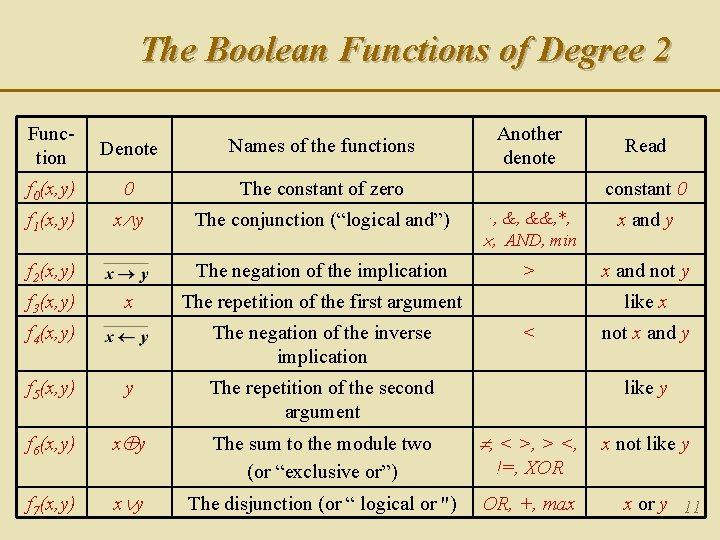
The Boolean Functions of Degree 2 Function Denote Names of the functions f 0(x, y) 0 The constant of zero f 1(x, y) x y The conjunction (“logical and”) ·, &, &&, *, , AND, min x and y The negation of the implication > x and not y f 2(x, y) f 3(x, y) x f 4(x, y) Another denote constant 0 The repetition of the first argument The negation of the inverse implication f 5(x, y) y The repetition of the second argument f 6(x, y) x y The sum to the module two (or “exclusive or”) f 7(x, y) x y The disjunction (or “ logical or ") Read like x < not x and y like y , < >, > <, x not like y !=, XOR OR, +, max x or у 11

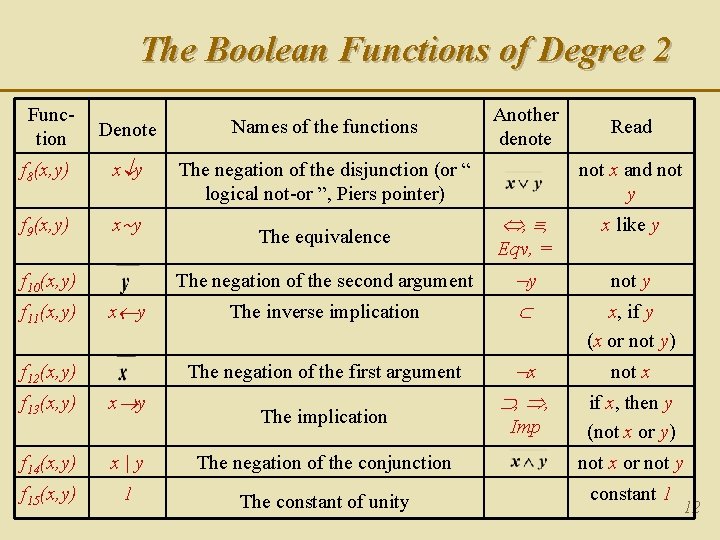
The Boolean Functions of Degree 2 Function Denote Names of the functions f 8(x, y) x y The negation of the disjunction (or “ logical not-or ”, Piers pointer) f 9(x, y) x y f 10(x, y) f 11(x, y) The equivalence The negation of the second argument x y f 12(x, y) The inverse implication The negation of the first argument f 13(x, y) x y f 14(x, y) x | y The negation of the conjunction f 15(x, y) 1 The constant of unity The implication Another denote Read not x and not y , , x like y Eqv, = y x , , not y x, if y (x or not y) not x Imp if x, then y (not x or y) not x or not y constant 1 12

Methods of Boolean function representation II. Numbers of Boolean functions and interpretations Every function has a sequence number as a natural number a binary code of which is a column of function values in a truth table. A least significant bit is consider a lowermost row (value of function on interpretation (1, 1, . , 1)), and senior — most overhead (value of function on interpretation (0, 0, . , 0)). 13

Methods of Boolean function representation Every interpretation of Boolean function has the number – value of binary code which is interpretation. Interpretation, which is written in the overhead row of truth table, has a number 0, after interpretation has number 1 and etc. In a lowermost row interpretation is located with a number 2 n– 1, where n is an amount of variables which depends a Boolean function. 14

Example Find the sequence number for function f(x, y), which has next values: f(0, 0)=1, f(0, 1)=1, f(1, 0)=0, f(1, 1)=1. x 0 0 1 1 y f(x, y) 0 1 1 1 0 0 1 1 Binary code for the value of this function – 11012 = 1 23 +1 22 +0 21 +1 20 = =8+4+0+1=1310 Thus, f 13(x, y) = (1101)2 15

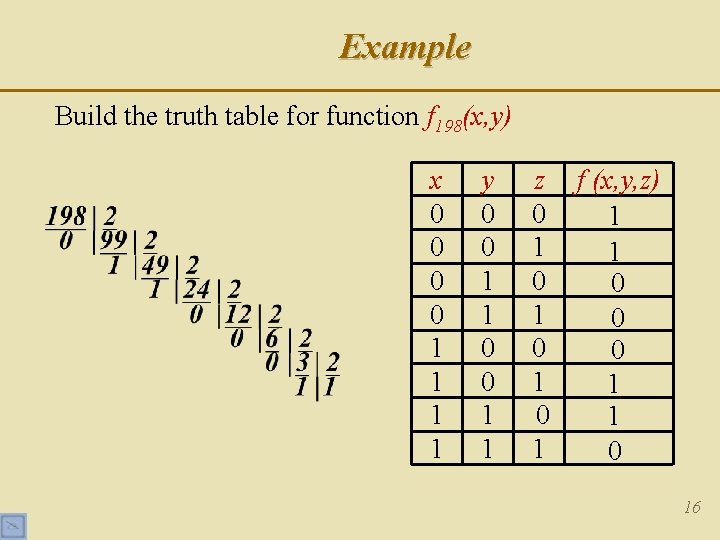
Example Build the truth table for function f 198(x, y) x 0 0 1 1 y 0 0 1 1 z f (x, y, z) 0 1 1 1 0 0 0 1 1 0 16

Methods of Boolean function representation III. Boolean function representation with using formulas A formula is expression which propose some function as superposition of another functions. Superposition is a method of new functions construction by the substitution of one function values in place of argument values of another function 17

Example Consider the formula of boolean algebra for function f(x, y, z) This formula has functions: g(x 1) – negation, s(x 1, x 2) – conjunction, l(x 1, x 2) – disjunction. Present this formula as superposition of the indicated functions as follows: f (x, y, z) = l(s(x, g(y)), z) 18

Precedence of operations 1. Negation. 2. Conjunction. 3. Disjunction. 4. Implication. 5. Equivalence. – ~ Example Clean all possible brackets Add some brackets taking into account precedence of operations 19

Equivalent function Two different Boolean expressions that represent the same function are called equivalent For instance, all the Boolean expressions xy 1, xy 0, and xy are equivalent. 20

Boolean Identities 1) Commutative laws x y = y x 2) Associative laws x (y z)= (x y) z x (y z)=(x y) z 3) Distributive laws x (y z) = (x y) (x z) 21

Boolean Identities 4) Idempotent laws x x = x 5) The excluded middle law 1 6) The contradiction law 0 7) The absorption laws (elimination laws) x x (x y) = x 22

Boolean Identities 8) Identity laws x 0 = x x 1 = x 9) Domination laws x 1 = 1 x 0 = 0 10) Law of the double negation x 11) De Morgan`s laws 23

Topic 2 Duality ХНУРЭ, кафедра ПО ЭВМ, Тел. 7021 -446, e-mail: belous@kture. Kharkov. ua

Dual Boolean function Function f*(x 1, …, xn) is called dual to function f(x 1, …, xn), if 25

Selfdual Boolean function A Boolean function is called selfdual if 26

Selfdual Boolean function It is easy to define if a given Boolean function is selfdual or not by its truth table. For this we divide a truth table by half, using the symmetrical line. If any arc connects equal values, then the function is not selfdual. If every arc connects different values, then the function is selfdual. 27

Selfdual Boolean function Example. Define if the function f 14(x, y) is selfdual. Solution. x y f 14 = x|y 0 0 1 0 1 1 1 0 Given function is not selfdual. 28

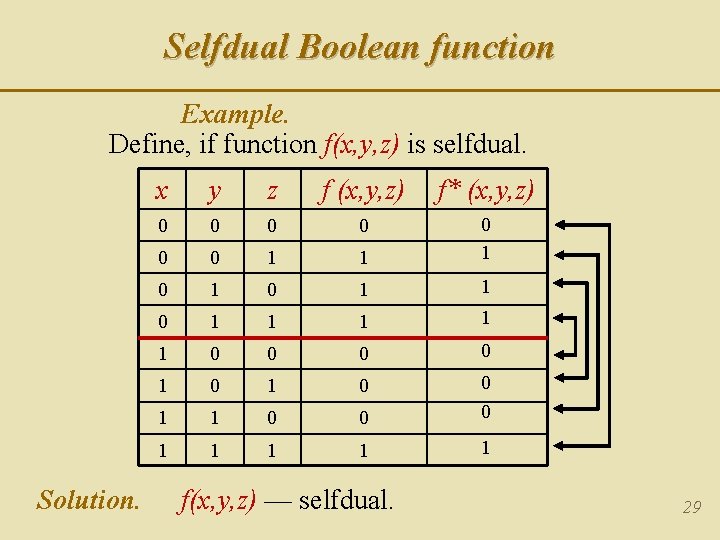
Selfdual Boolean function Example. Define, if function f(x, y, z) is selfdual. x y z f (x, y, z) f* (x, y, z) 0 0 0 1 1 0 1 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 Solution. f(x, y, z) — selfdual. 29

Duality principle The function f is given by superposition of function f 0, …, fn, where n N. Function f*, dual to f, can be obtained, changing functions f 0, …, fn in the formula f for dual to f 0*, …, fn*. 30

Duality principle Example. Find dual functions. Solution. 31

Rule of obtaining dual formula To obtain dual formula of Boolean algebra it is needed to change all conjunctions for disjunctions, disjunctions for conjunctions, 0 for 1, 1 for 0 in it, and use brackets where it is needed to keep previous order of fulfilling operations. 32

Rule of obtaining dual formula Example. Find function dual to function Solution. Let’s use previous rule of obtaining dual formula. 33

Rule of obtaining dual formula If functions are equal then dual to them functions are equal too. Let f 1 and f 2 are some functions expressing by such formulas. If f 1 = f 2 , then f 1* = f 2* 34