Discrete Mathematics adjacency matrix incidence matrix subgraph graph

Discrete Mathematics adjacency matrix, incidence matrix, subgraph, graph operations, degree, handshaking theorem, graph isomorphism Liangfeng Zhang School of Information Science and Technology Shanghai. Tech University

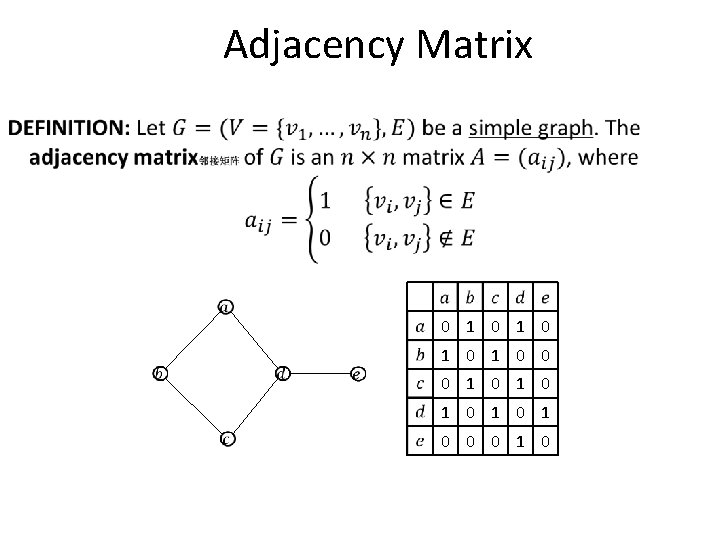
Adjacency Matrix 0 1 0 1 0 0 0 1 0

Adjacency Matrix 2 1 0 1 0 1 1 0 0 1 0 2 0 1 1 2 0 1 0 0 0 1 0

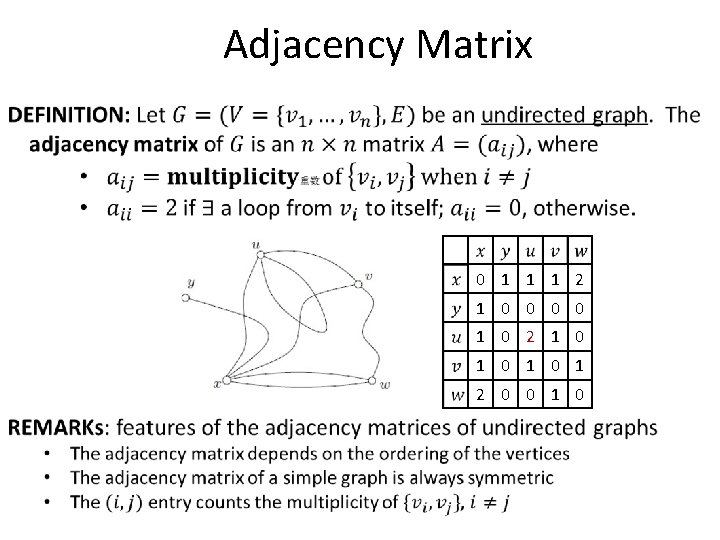
Adjacency Matrix 0 1 1 1 2 1 0 0 1 0 2 1 0 1 0 1 2 0 0 1 0

Adjacency Matrix 0 1 0 0 0 0 1 0 REMARKS: The adjacency matrix is no longer symmetric

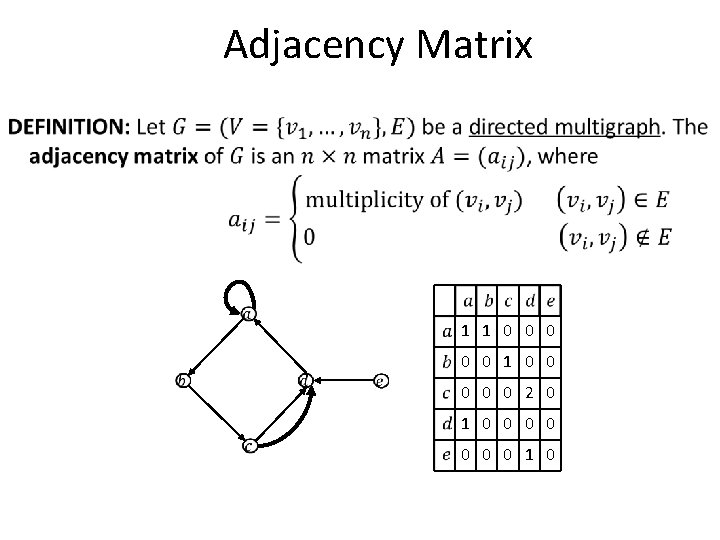
Adjacency Matrix 1 1 0 0 0 0 0 2 0 1 0 0 0 0 1 0

Incidence Matrix

Subgraph

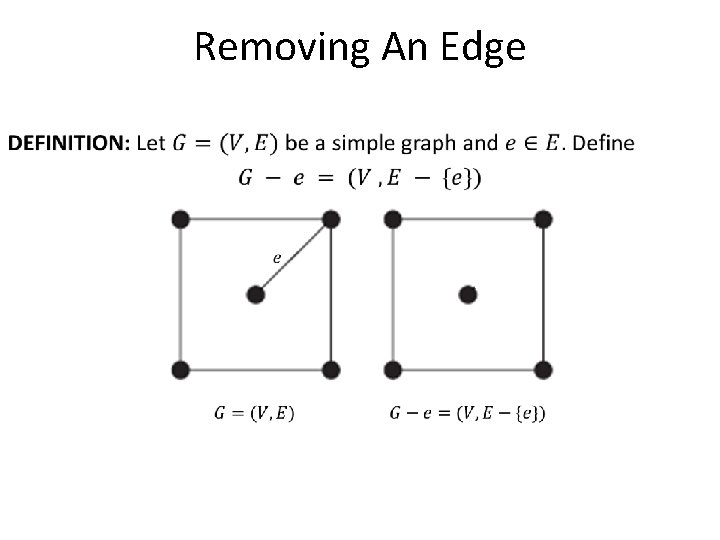
Removing An Edge

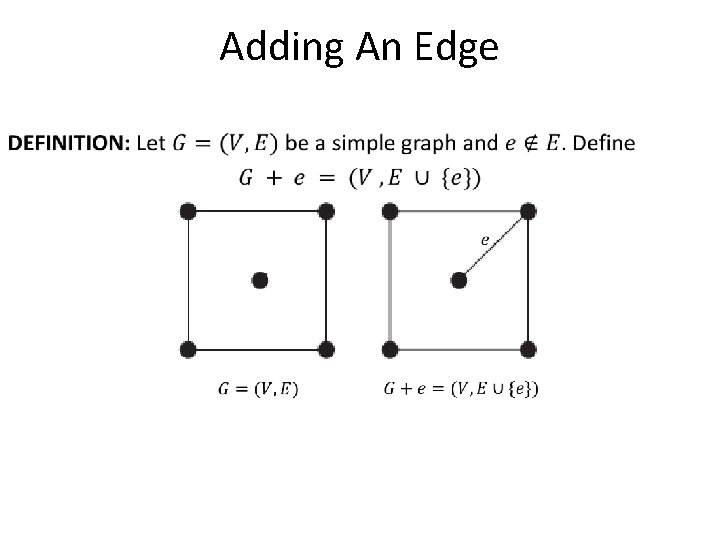
Adding An Edge

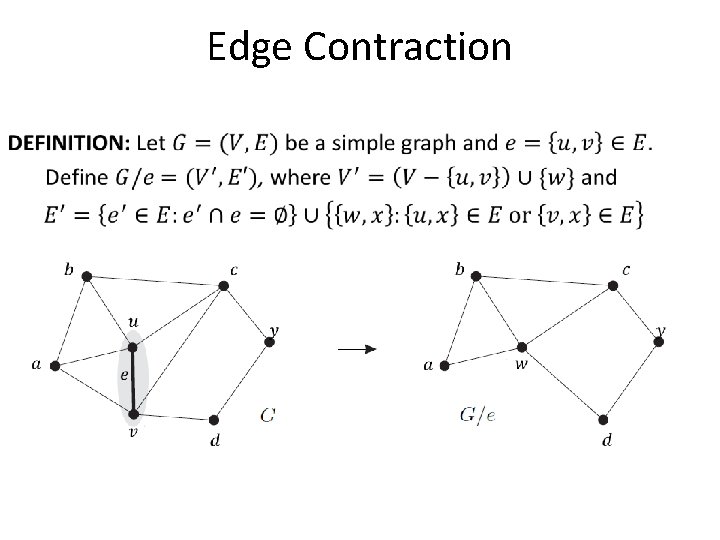
Edge Contraction

Removing A Vertex

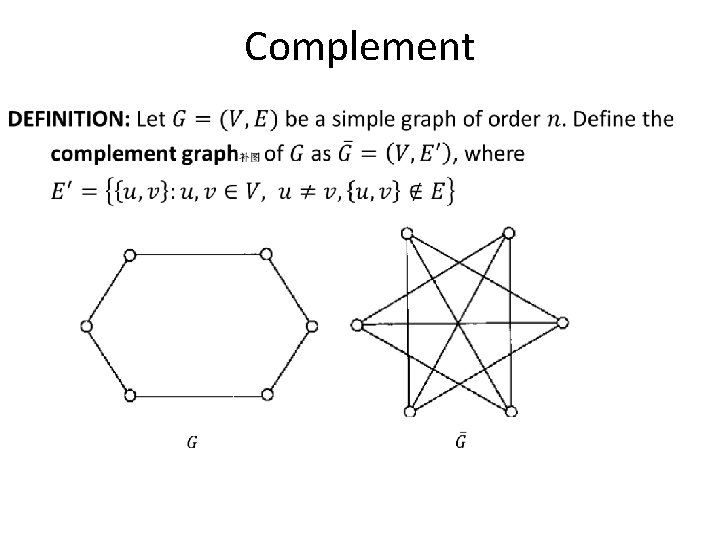
Complement

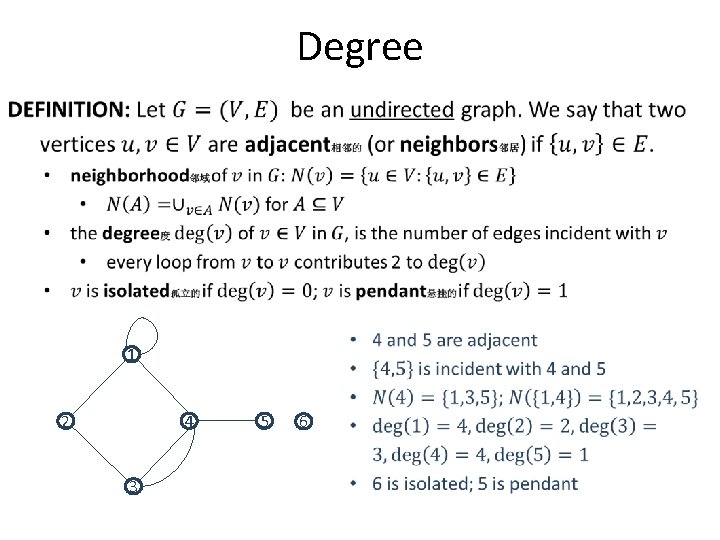
Degree 1 2 4 3 5 6

Degree 1 2 4 3 5 6

Handshaking Theorem

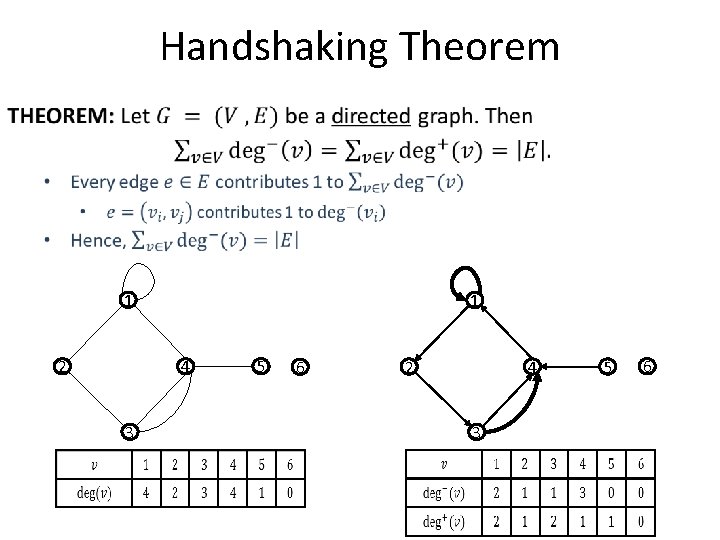
Handshaking Theorem 1 2 1 4 3 5 6 2 4 3 5 6

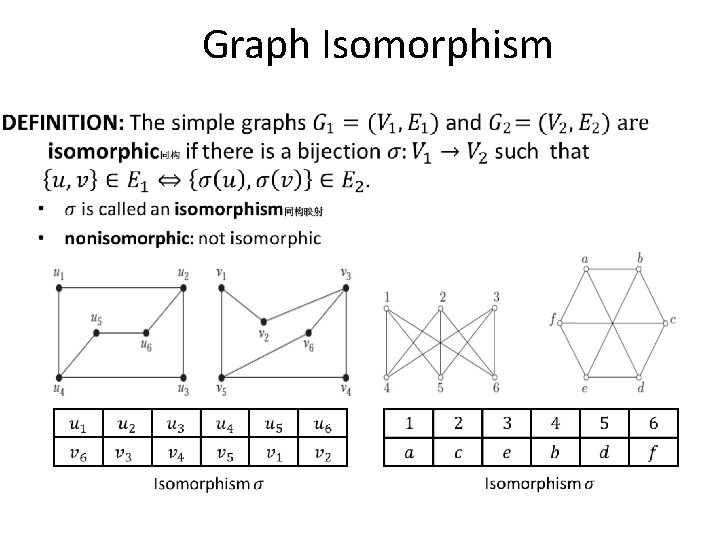
Graph Isomorphism

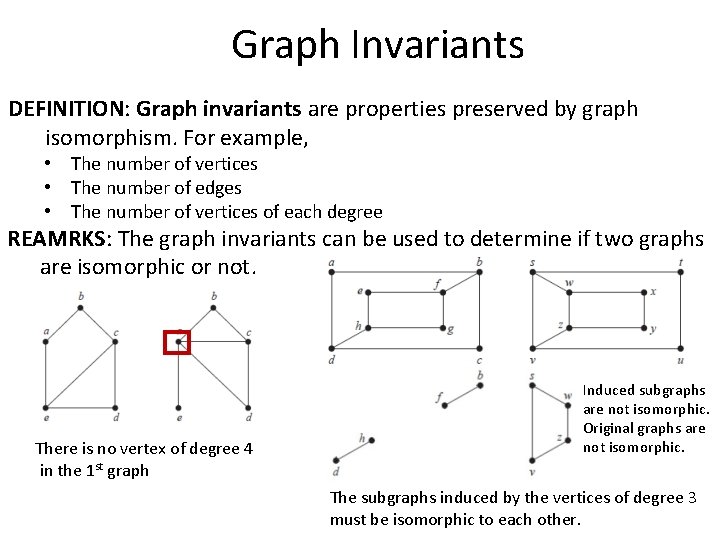
Graph Invariants DEFINITION: Graph invariants are properties preserved by graph isomorphism. For example, • The number of vertices • The number of edges • The number of vertices of each degree REAMRKS: The graph invariants can be used to determine if two graphs are isomorphic or not. There is no vertex of degree 4 in the 1 st graph Induced subgraphs are not isomorphic. Original graphs are not isomorphic. The subgraphs induced by the vertices of degree 3 must be isomorphic to each other.