Discrete Mathematical Set Theory Definitions and notation A

Discrete Mathematical

Set Theory - Definitions and notation A set is an unordered collection of elements. Some examples: {1, 2, 3} is the set containing “ 1” and “ 2” and “ 3. ” {1, 1, 2, 3, 3} = {1, 2, 3} since repetition is irrelevant. {1, 2, 3} = {3, 2, 1} since sets are unordered. {1, 2, 3, …} is a way we denote an infinite set (in this case, the natural numbers). = {} is the empty set, or the set containing no elements. Note: { }

Set Theory - Definitions and notation x S means “x is an element of set S. ” x S means “x is not an element of set S. ” A B means “A is a subset of B. ” or, “B contains A. ” or, “every element of A is also in B. ” or, x ((x A) (x B)). A B Venn Diagram

Set Theory - Definitions and notation A B means “A is a subset of B. ” A B means “A is a superset of B. ” A = B if and only if A and B have exactly the same elements. iff, A B and B A iff, A B and A B iff, x ((x A) (x B)). So to show equality of sets A and B, show: • • A B B A

Set Theory - Definitions and notation A B means “A is a proper subset of B. ” • • • A B, and A B. x ((x A) (x B)) x ((x B) (x A)) x ( (x B) v (x A)) x ((x B) (x A)) A B

Set Theory - Definitions and notation Quick examples: {1, 2, 3} {1, 2, 3, 4, 5} Is {1, 2, 3}? Yes! x (x ) (x {1, 2, 3}) Vacuously holds, because (x ) is false. Is {1, 2, 3}? No! Is { , 1, 2, 3}? Yes!

Set Theory - Definitions and notation Quiz time: Is {x}? Yes Is {x} {x, {x}}? Yes Is {x}? No

Set Theory - Ways to define sets : and | are read Explicitly: {John, Paul, George, Ringo} “such that” or Implicitly: {1, 2, 3, …}, or {2, 3, 5, 7, 11, 13, 17, …} “where” Set builder: { x : x is prime }, { x | x is odd }. In general { x : P(x) is true }, where P(x) is some description of the set. Ex. Let D(x, y) denote “x is divisible by y. ” Give another name for { x : y ((y > 1) (y < x)) D(x, y) }. Primes

Set Theory - Cardinality If S is finite, then the cardinality of S, |S|, is the number of distinct elements in S. If S = {1, 2, 3}, |S| = 3. |S| = 1. If S = {3, 3, 3}, If S = , |S| = 0. If S = { , { }, { }} }, |S| = 3. If S = {0, 1, 2, 3, …}, |S| is infinite. (more on this later)

Set Theory - Power sets If S is a set, then the power set of S is 2 S = { x : x S }. aka P(S) If S = {a}, 2 S = { , {a}}. If S = {a, b}, 2 S = { , {a}, {b}, {a, b}}. If S = , We say, “P(S) is the set of all subsets of S. ” 2 S = { }. If S = { , { }}, 2 S = { , { }, {{ }}, { }}}. Fact: if S is finite, |2 S| = 2|S|. (if |S| = n, |2 S| = 2 n) aka = also known as

Set Theory - Cartesian Product The Cartesian Product of two sets A and B is: A x B = { <a, b> : a A b B} If A = {Charlie, Lucy, Linus}, and B = {Brown, Van. Pelt}, then A x B = {<Charlie, Brown>, <Lucy, Brown>, <Linus, Brown>, <Charlie, Van. Pelt>, <Lucy, Van. Pelt>, <Linus, Van. Pelt>} A 1 x A 2 x … x An = {<a 1, a 2, …, an>: a 1 A 1, a 2 A 2, …, a n A n} A, B finite |Ax. B| = ?

Set Theory - Operators The union of two sets A and B is: A B = { x : x A v x B} If A = {Charlie, Lucy, Linus}, and B = {Lucy, Desi}, then A B = {Charlie, Lucy, Linus, Desi} B A

Set Theory - Operators The intersection of two sets A and B is: A B = { x : x A x B} If A = {Charlie, Lucy, Linus}, and B = {Lucy, Desi}, then A B = {Lucy} B A

Set Theory - Operators The intersection of two sets A and B is: A B = { x : x A x B} If A = {x : x is a US president}, and B = {x : x is deceased}, then A B = {x : x is a deceased US president} B A

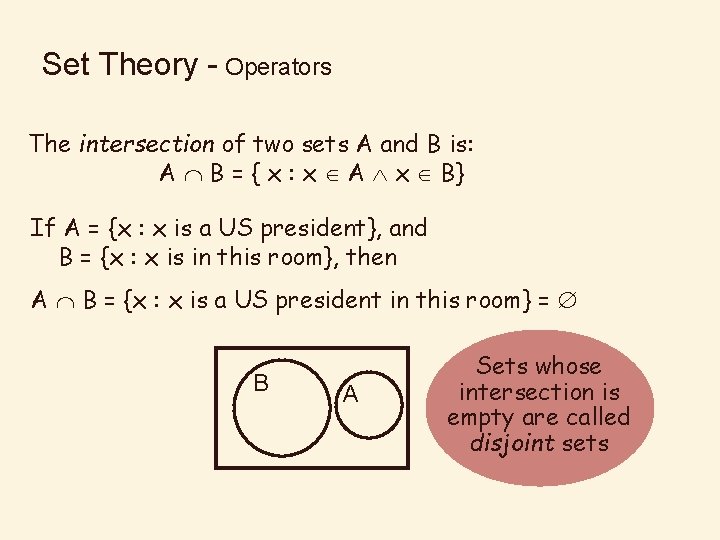
Set Theory - Operators The intersection of two sets A and B is: A B = { x : x A x B} If A = {x : x is a US president}, and B = {x : x is in this room}, then A B = {x : x is a US president in this room} = B A Sets whose intersection is empty are called disjoint sets

Set Theory - Operators The complement of a set A is: A = { x : x A} If A = {x : x is bored}, then A = {x : x is not bored} = U A = U and U=

Set Theory - Operators The set difference, A - B, is: U A B A-B={x: x A x B} A-B=A B

Set Theory - Operators like “exclusive or” The symmetric difference, A B, is: A B = { x : (x A x B) v (x B x A)} = (A - B) U (B - A) U A B

Set Theory - Operators A B = { x : (x A x B) v (x B x A)} = (A - B) U (B - A) Proof: { x : (x A x B) v (x B x A)} = { x : (x A - B) v (x B - A)} = { x : x ((A - B) U (B - A))} = (A - B) U (B - A)

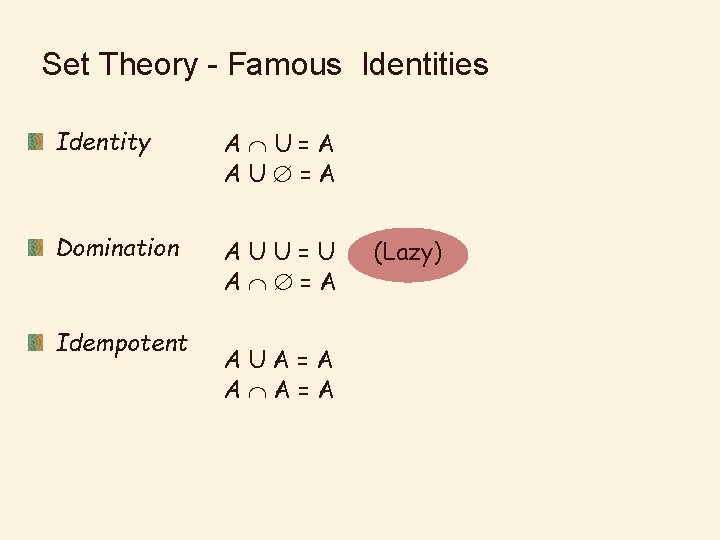
Set Theory - Famous Identities Identity A U=A AU =A Domination AUU=U A =A Idempotent AUA=A A A=A (Lazy)

Set Theory - Famous Identities Excluded Middle A U A = U Uniqueness A A= Double complement A=A

Set Theory - Famous Identities Commutativity AUB= BUA A B= B A Associativity (A U B) U C = A U (B U C) (A B) C = A (B C) Distributivity A U (B C) = (A U B) (A U C) A (B U C) = (A B) U (A C)

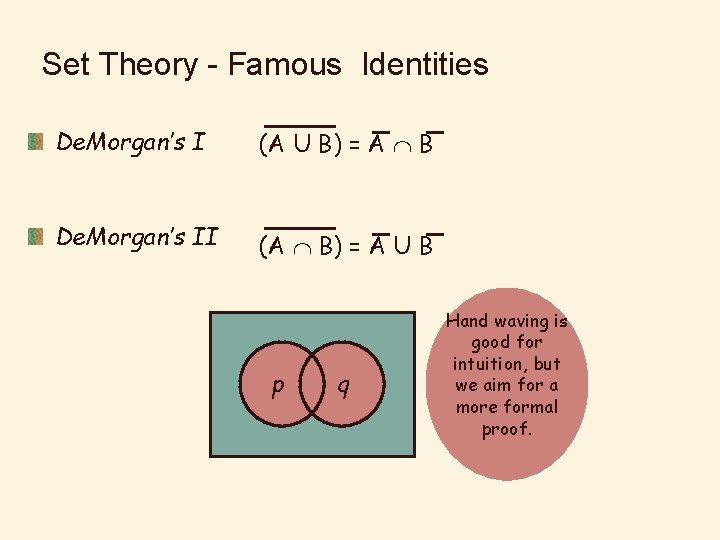
Set Theory - Famous Identities De. Morgan’s I (A U B) = A B De. Morgan’s II (A B) = A U B p q Hand waving is good for intuition, but we aim for a more formal proof.

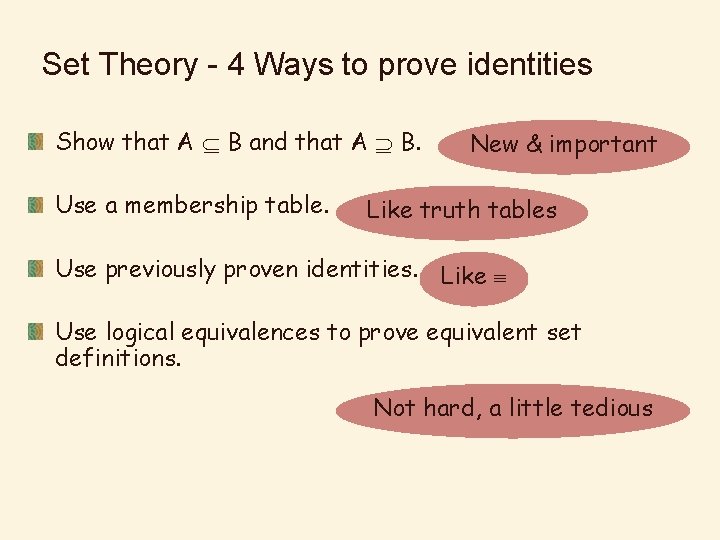
Set Theory - 4 Ways to prove identities Show that A B and that A B. Use a membership table. New & important Like truth tables Use previously proven identities. Like Use logical equivalences to prove equivalent set definitions. Not hard, a little tedious

Set Theory - 4 Ways to prove identities Prove that (A U B) = A B 1. ( ) (x A U B) (x A and x B) (x A B) 2. ( ) (x A B) (x A and x B) (x A U B)

Set Theory - 4 Ways to prove identities Prove that (A U B) = A B using a membership table. 0 : x is not in the specified set 1 : otherwise A B A B AUB 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1

Set Theory - 4 Ways to prove identities Prove that (A U B) = A B using identities. (A U B) = A U B =A B