Discrete Math for CS LECTURE 24 Last time

Discrete Math for CS LECTURE 24 Last time: • Graphs. • Eulerian tours Today: • Hamiltonian paths and tours. • Important classes of graphs 3/3/2021

Reminders • A tour (or a walk) that visits each edge in a multigraph exactly once is called Eulerian. • Euler’s Theorem. A multigraph G has a Eulerian tour iff G is connected (except possibly for isolated vertices) and every vertex in G has even degree. • Corollary of Euler’s Theorem. A multigraph G has a Eulerian walk iff G is connected (except possibly for isolated vertices) and the number of vertices of odd degree in G is 0 or 2. 3/3/2021

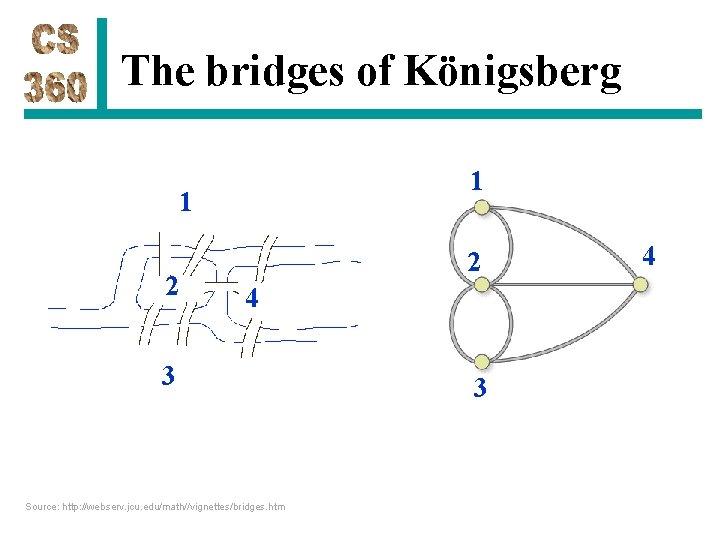
The bridges of Königsberg 1 1 2 2 4 3 Source: http: //webserv. jcu. edu/math//vignettes/bridges. htm 3 4

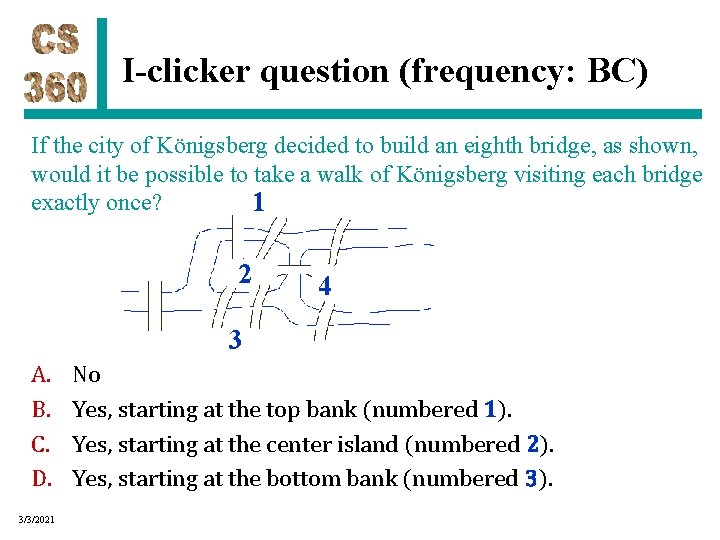
I-clicker question (frequency: BC) If the city of Königsberg decided to build an eighth bridge, as shown, would it be possible to take a walk of Königsberg visiting each bridge exactly once? 1 2 4 3 A. B. C. D. 3/3/2021 No Yes, starting at the top bank (numbered 1). Yes, starting at the center island (numbered 2). Yes, starting at the bottom bank (numbered 3).

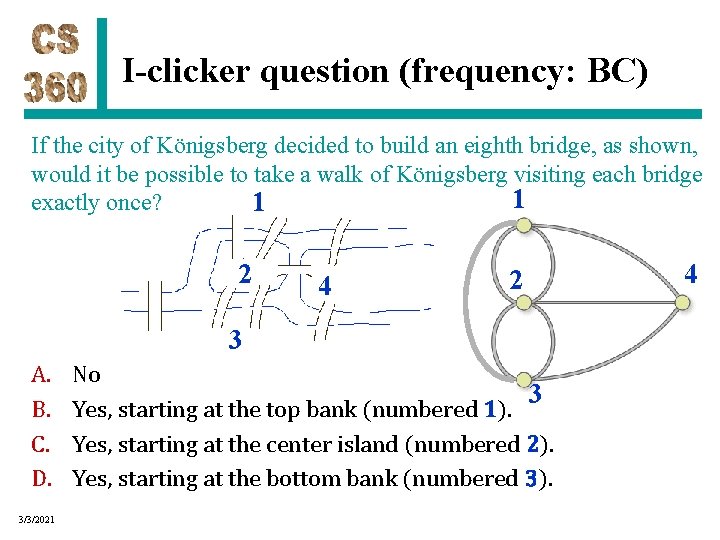
I-clicker question (frequency: BC) If the city of Königsberg decided to build an eighth bridge, as shown, would it be possible to take a walk of Königsberg visiting each bridge 1 exactly once? 1 2 4 2 3 A. B. C. D. 3/3/2021 No 3 Yes, starting at the top bank (numbered 1). Yes, starting at the center island (numbered 2). Yes, starting at the bottom bank (numbered 3). 4

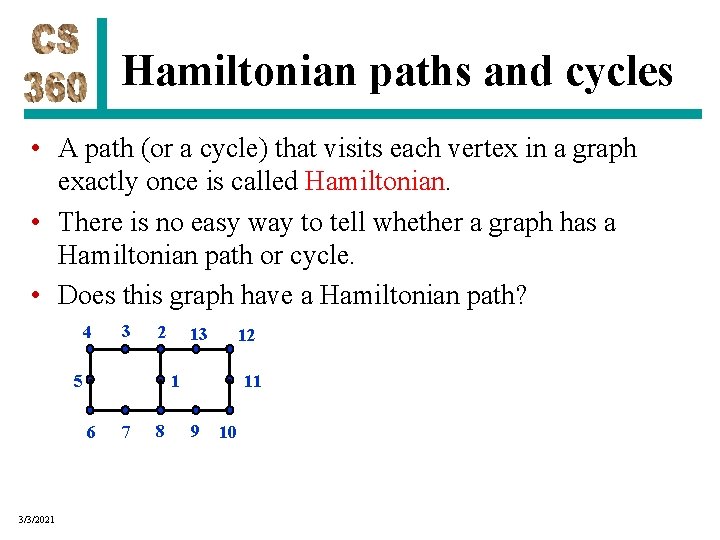
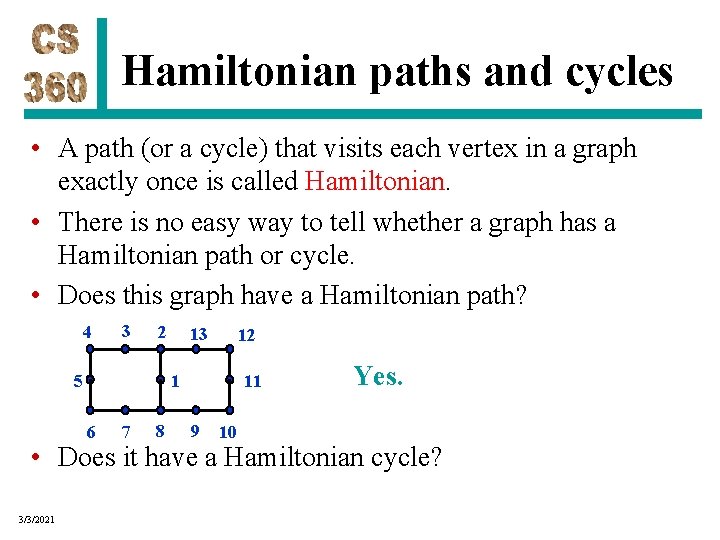
Hamiltonian paths and cycles • A path (or a cycle) that visits each vertex in a graph exactly once is called Hamiltonian. • There is no easy way to tell whether a graph has a Hamiltonian path or cycle. • Does this graph have a Hamiltonian path? 4 3 2 12 1 5 6 3/3/2021 13 7 8 11 9 10

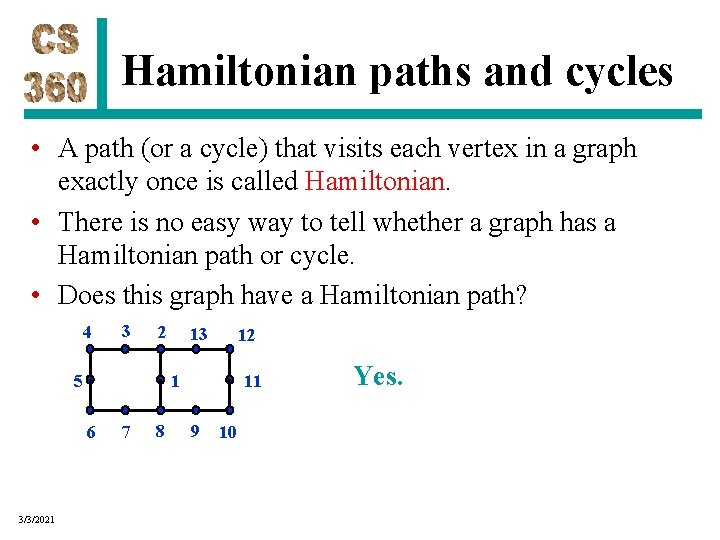
Hamiltonian paths and cycles • A path (or a cycle) that visits each vertex in a graph exactly once is called Hamiltonian. • There is no easy way to tell whether a graph has a Hamiltonian path or cycle. • Does this graph have a Hamiltonian path? 4 3 2 13 12 Yes. 1 5 11 6 7 8 9 10 • Does it have a Hamiltonian cycle? 3/3/2021

Hamiltonian paths and cycles • A path (or a cycle) that visits each vertex in a graph exactly once is called Hamiltonian. • There is no easy way to tell whether a graph has a Hamiltonian path or cycle. • Does this graph have a Hamiltonian path? 4 3 2 13 12 Yes. 1 5 11 6 3/3/2021 7 8 9 10

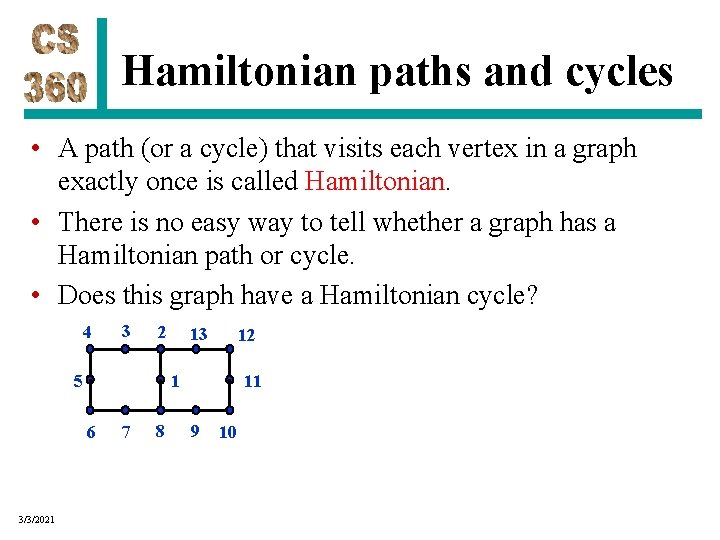
Hamiltonian paths and cycles • A path (or a cycle) that visits each vertex in a graph exactly once is called Hamiltonian. • There is no easy way to tell whether a graph has a Hamiltonian path or cycle. • Does this graph have a Hamiltonian cycle? 4 3 2 13 12 1 5 11 6 3/3/2021 7 8 9 10

Hamiltonian paths and cycles • A path (or a cycle) that visits each vertex in a graph exactly once is called Hamiltonian. • There is no easy way to tell whether a graph has a Hamiltonian path or cycle. • Does this graph have a Hamiltonian cycle? 4 3 2 13 12 No. 1 5 11 6 7 8 9 10 • Odd and even vertices would have to alternate in a Hamiltonian cycle. But we have 7 odd and 6 even! 3/3/2021

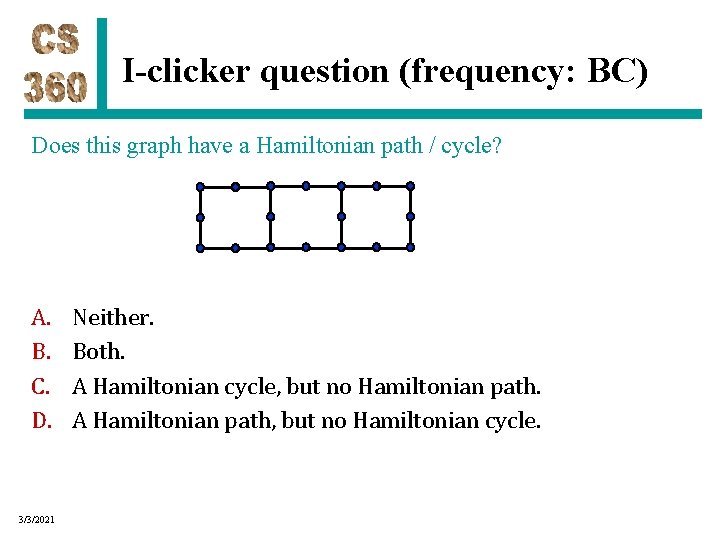
I-clicker question (frequency: BC) Does this graph have a Hamiltonian path / cycle? A. B. C. D. 3/3/2021 Neither. Both. A Hamiltonian cycle, but no Hamiltonian path. A Hamiltonian path, but no Hamiltonian cycle.

Important classes of graphs • • 3/3/2021 Complete graphs Cycles Trees Hypercubes

Complete graphs • 3/3/2021

Cycles • 3/3/2021

Trees (equivalent definitions) • 3/3/2021

Hypercubes • 3/3/2021